半导体Si和GaAs的GW近似能带结构与BSE吸收光谱的研究

杨俊涛，罗时军，黄海铭，熊永臣

（湖北汽车工业学院理学院，湖北十堰442002）

电子能带结构是半导体材料最基本的性质之一，对于半导体的实际应用具有深刻影响,同时，半导体能级结构的预测也是第一性原理理论方法中最具挑战性的问题之一。作为材料理论计算标准模型的密度泛函理论（DFT），存在着著名的“带隙问题”[1]：半导体材料的理论带隙与实验值相比存在着显著的系统性误差。而且半导体的光学性质的吸收光谱、发光光谱和激子效应等，均与电子激发状态有关，涉及到了电子—空穴对的多体效应。目前广泛采用建立在的DFT 理论上的局域密度（LDA）近似或广义梯度近似（GGA），均无法准确计算材料的电子结构，更难以预言具有动力学性质的激发态实验的结果。究其原因，DFT理论建立在单粒子近似的基础上，为了解决这一困境，许多多体微扰理论得以发展[2]，其中，基于格林函数的第一性原理的GW[3-4]方法是当前描述材料的电子能带结构最为准确的第一性原理方法。

笔者在DFT-GGA的基础上，采用准粒子近似的GW方法对半导体Si和GaAs的激发态电子结构的进行了计算，同时研究了其光学性质的吸收谱；在GW 基础上，利用多体微扰理论的Bethe-Salpeter方程（BSE），对Si和GaAs的光吸收谱进行了修正，并简要分析了激子效应对光谱吸收的作用。

1 模型和方法

本文中研究的对象是最为广泛使用的典型的半导体面心立方的Si 晶体和闪锌矿结构的GaAs晶体两类半导体材料，二者具有相似的能带结构，分别属于间接带隙和直接带隙半导体。在计算过程中，晶体的晶格常数使用的是实验值，考虑到光学性质的计算，采用Monkhorst-Pack方法对布里渊区的取样为使用15×15×15的较密k-mesh 网格。交换关联能采用的是基于平面缀加波的广义密度近似的PBE泛函[5]。首先利用DFT-PBE，计算了Si和GaAs 能带结构和介电函数，并采用准粒子近似的GW方法进行了修正；然后利用多体微扰方法的Bethe-Salpeter方程（BSE），进一步计算了Si和GaAs的光吸收谱。所有的计算均在VASP 模拟软件包中完成。

在多体微扰理论下，可由式（1）计算得出准粒子GW近似本征值Enk[6]：

式中∶T为动能算符；Vn-e为电子与原子核作用势；VH为Hartree 势；ψnk为波函数；n为能带；k为波矢点；∑为GW方法中的自能算符，其定义为

式中：G为格林函数(Green Function)，其作用是计算粒子由初始状态穿过多体系统到达新的状态所有可能路径的几率期望值；W为屏蔽库仑势(Screened Coulomb Potential)，描述了多体系统准粒子之间的相互作用，一般用原独立电子间库仑势除以介电函数计算。

从介电函数中，可计算获得半导体材料的光学性质，忽略电子—空穴对的激子效应，在对布里渊区的价带和导带的带间跃迁求和积分计算得到宏观的介电函数虚部[7]：

介电函数的实部可对虚部进行Kramer-Kronig变换求得。

半导体中被光激发的在导带中的电子与留在价带中的空穴之相互作用形成局域在带隙内的束缚态电子—空穴对，即激子（exciton）。半导体的光谱强烈地受激子效应的影响，为了描述半导体中的激子效应，必须正确处理电子—空穴对的相互作用，需求解BSE方程[8]：

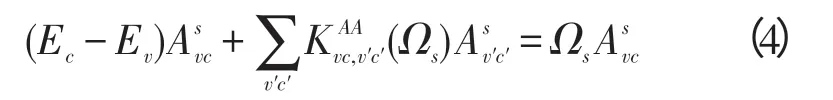
2 结果与讨论

2.1 能带结构修正

布里渊区沿特殊对称线的能带结构是利用在均匀k-mesh 网格上的GW 准粒子修正值和准粒子波函数构造Wannier 函数插值法得到[9]。GW方法和DFT-PBE方法计算所得的Si和GaAs 沿高对称点的能带结构如图1所示。

从图1可以看出，整体上，DFT-PBE和GW方法计算的能带的色散关系基本一致，但对不同的能带和不同的k点，GW方法的修正值有细微的变化。准粒子的GW 近似计算得到的Si 属于间接带隙结构，其价带顶均位于Γ点，导带底位于X点；GaAs 属于直接带隙结构，价带顶和导带低均位于Γ点，这与DFT-PBE的计算结果相同。相对于DFT-PBE，GW方法所得的能带结构中，价带的本征值降低，而导带的本征值升高，直接结果是，GW预测的半导体能隙值相对于DFT-PBE的结果明显增加，并更接近于实验值，见表1。其中，Si的能隙的GW 计算值1.10eV要比DFT-PBE的0.47eV更接近于实验值1.17eV；相比DFT-PBE的GaAs的0.56eV直接能隙，的GW 计算结果为1.28eV更接近于实验值1.52eV。很显然，考虑了准粒子近似的GW方法比单粒子近似的DFT方法对半导体能隙的预测要准确很多。

图1 能带图

表1 Si和GaAs的带隙与介电常数理论值与实验值[10]

2.2 光学性质

在完成能级结构计算后，分别采用了单粒子近似的DFT-PBE方法，准粒子近似的GW方法和考虑了电子—空穴对效应的BSE方程对Si和GaAs的介电函数的虚部ε"(ω)，即光吸收谱进行了计算，如图2所示，并给出了相应的实验值便于比较。由于不考虑电子空穴相互互作，光吸收谱完全取决于半导体的能级结构，故GW 光吸收谱和DFT-PBE 光吸收谱特性基本一致，但向高能量区产生距离相当于能隙修正值的蓝移，比如Si 大约0.60eV，故图2中没有给出DFT-PBE的光吸收谱。

从图2可看出，只考虑准粒子近似GW方法得到的Si的吸收光谱和实验值比较起来有较大偏差，在3.3eV处的峰值不到20，远低于约35的实验值，而在4.8eV处，有一极大的峰值。BSE方程得到的Si 光吸收谱和实验曲线[8]的符合度很高，由于电子—空穴对的激子效应，3.3eV处的峰值急剧增高，并接近于实验值；相对于出的突兀峰，在4.8eV的峰值下降很多。相对于实验值，和在3.5eV出都有一劈裂峰，这与能级结构的高简并度有关；有大约有0.4eV的红移，这应该与计算的精度设置以及k-mesh的密度有关。对于GaAs，其光吸收谱的计算结果和Si类似，要比更符合实验曲线[11]。GaAs 属于直接带隙半导体，且带隙较窄，在1.5eV左右的2个峰值则与Γ点处的激子吸收有关。相对于单晶Si，GaAs的理论吸收光谱有更多的劈裂峰，这源于Ga与As的轨道杂化作用。表1列出了Si和GaAs 介电函数的静态理论计算值和实验值,可以看出，其理论值随 εPBE(0)，εGW(0)和εBSE(0)逐步逼近实验值。不过εBSE(0)仍然稍大于实验值，这是由于在计算中没有考虑无规相近似（Radom Phase Approximation)的结果。

图2 介电函数曲线

3 结论

在基于平面缀加波的广义密度近似的PBE 泛函的基础上，采用准粒子近似的GW方法对典型的半导体硅Si和砷化镓GaAs的能带结构进行了研究；Si的间接能隙的GW 计算值1.10eV要比DFTPBE的0.47eV更接近于实验值1.17eV；相比DFTPBE的GaAs的0.56eV直接能隙，GW 计算结果为1.28eV更接近于实验值1.52eV。GW方法计算的光吸收谱和DFT-PBE 光吸收谱特性基本一致，但向高能量区产生距离相当于能隙修正值的蓝移，与实验值符合不佳。在GW 基础上，利用多体微扰理论的Bethe-Salpeter方程，对Si和GaAs的光吸收谱进行了修正，考虑了电子—空穴对激子效应的GW-BSE多体微扰方法计算的Si和GaAs的介电函数吸收谱与实验曲线十分吻合；说明的准粒子近似和激子效应在半导体性质研究能级结构研究和光谱分析方面十分重要。

[1]Jiang Hong.The GW Method：Basic Principles，Latest Developments and Its Applications for d- and f-Electron Systems[J].Acta Phys.-Chim.Sin.，2010，26（4）：1017-1033.

[2]韩汝珊.凝聚态物理从头计算的最新进展[J].物理，2011,39（11）：753-764.

[3]L.Hedin.New method for calculating the one-particle Green′s function with application to the electron- gas problem[J].Phys.Rev.，1965（139）：A796-A823.

[4]F.Aryasetiawan，O.Gunnarsson.The GW method[J].Rep.Prog.Phys.,1998,61（237）：237-312.

[5]John P.Perdew，J.A.Chevary，S.H.Vosko，etc.Atoms，molecules，solids，and surfaces：Applications of the generalized gradient approximation for exchange and correlation[J].Phys.Rev.B，1992（46）：6671-6687.

[6]M.Shishkin and G.Kresse，Implementation and performance of the frequency-dependent GW method within the PAW framework[J].Phys.Rev.B，2006（74）：035101-035114.

[7]J.Furthmüller and F.Bechstedt.Linear optical properties in the projector-augmented wave methodology[J].Phys.Rev.B，2006（73）：045112-045121.

[8]M.Rohlfing and S.G.Louie，Electron-hole excitations and optical spectra from first principles[J].Phys.Rev.B，2000，62（8）：4927–4944.

[9]Hamann.D.R，Vanderbilt.D.Maximally localized Wannier functions for GW quasiparticles[J].Phys.Rev.B，2009（79）：045109-045118.

[10]F.Fuchs，J.Furthmüller，etc.Quasiparticle band structure based on a generalized Kohn-Sham scheme[J].Phys.Rev.B，2007（76）：115109-115116.

[11]Brozel，M.R.，Stillman，G.E.Properties of gallium arsenide[M].3th ed.London：INSPEC Press，1996：8-948.