谐波电网电压下基于矢量谐振控制的双馈异步发电机集成控制策略

宋亦鹏 年 珩

（浙江大学电气工程学院 杭州 310027）

1 引言

随着能源和环境问题的日益严峻，可再生能源发电技术，特别是风力发电技术得到了广泛关注和长足发展，其中基于双馈异步发电机（Doubly Fed Induction Generator,DFIG）的风电系统应用最为广泛[1,2]。为实现风电机组的并网发电运行，DFIG 系统采用网侧及转子侧两个PWM 变流器，网侧变流器用于维持直流母线电压的恒定及调节网侧功率因数，而转子侧变流器可对定子输出有功功率和无功功率进行独立控制[3-5]。

目前理想电网电压下的DFIG 控制技术已经十分成熟，在此基础上考虑电网不平衡的DFIG 控制技术得到了广泛的研究[6-9]。然而实际电网中，一定含量的谐波电压分量总是不可避免的存在，IEEE 519—1992[10]及 ERG5/4—1[11]等标准中规定电网电压中允许存在不超过5%的5 次、7 次谐波分量。若DFIG 采用传统的控制策略，将出现定转子电流畸变、定子输出有功及无功功率和电磁转矩波动，不利于DFIG 风电机组以及电网的稳定可靠运行[12-16]。

为了改善 DFIG 在谐波电网电压下的运行性能，文献[17]给出了在微网运行条件下，通过对DFIG 的有效控制策略达到抑制或消除微网中包含的谐波及负序电压分量，进而提高微网电能质量。然而，考虑到DFIG 机组容量相对较小，此方法难以应用于大电网并网发电的应用场合。文献[18,19]在传统DFIG 拓扑结构的基础上，在电机定子绕组与电网之间串联接入变流器，通过对变流器的有效控制，使得其达到补偿电网中的负序分量，以确保DFIG 在电网跌落或者不平衡等故障条件下依然能够采用传统控制策略，但该控制策略需增加DFIG系统复杂性和硬件成本。文献[20]通过分别建立基波和谐波旋转坐标系下的DFIG 数学模型，提出了考虑5 次、7 次谐波电压下的谐波优化控制目标，以分别减少定子和转子电流畸变，定子输出有功/无功功率及电磁转矩波动为目标的谐波控制策略。为达到上述谐波控制目标，不仅需要实时准确检测电网电压所包含的谐波分量阶次及含量，还须对不同谐波控制目标下转子参考电流值进行复杂的数学运算。目前，常用于谐波分量提取的技术有以下几类[19-24]:①陷波器方法；②低通滤波器方法；③瞬时有功/无功功率方法；④瞬时有功/无功电流方法。其中方法①将待求的谐波分量变换至对应的谐波频率旋转坐标系，用陷波器滤除基频及其余各次谐波分量以得到待求谐波分量的幅值[19-23]。但该方法需用到大量的坐标变换和陷波器，不仅对DSP 带来较多的计算任务，还需使用低通滤波器以滤除高频干扰信号，因此无法满足谐波电网下DFIG 的高性能实时控制要求。方法②，③，④通过求得电网电压中的基频分量，用此基频信号与原始信号相减，得到有关电网谐波电压分量的信息。但这些方法得到的电网谐波电压信号为所有谐波分量之和，而无法得到各个谐波信号的幅值信息，故无法满足DFIG不同谐波目标的控制要求[24]。

为了降低谐波电网下 DFIG 控制的运算复杂性，进而提高DFIG 的稳态及暂态运行性能，文献[25]通过在转子电流闭环PI 调节中加入定子电流谐振闭环控制，以实现DFIG 正弦定子电流的控制目标，其中转子电流PI 调节用于实现DFIG 风电机组最大风能追踪所需的功率控制，定子电流谐振闭环控制用于实现谐波电网下注入电网的定子电流始终保持正弦。文献[25]所提出的谐波控制策略无需文献[19-23]中的电网电压谐波分量提取环节，也无需计算特定谐波控制目标下的转子电流参考值，因此有助于谐波电网下DFIG 高性能控制的工程实现。但文献[25]采用普通的谐振控制器难以消除 DFIG传递函数中的极点，进而导致闭环控制运行不稳定，此外采用普通谐振器还存在闭环相位响应精度问题，会增大闭环系统的稳态及动态控制误差，不利于 DFIG 系统在谐波电网下对谐波电流的精确控制。文献[26]通过对比普通谐振控制器和矢量谐振控制器，说明矢量谐振控制器可通过合理设计谐振参数，以消除DFIG 传递函数极点，增强系统闭环运行稳定性，因此矢量谐振控制器更适用于DFIG在谐波电网下控制目标的实现[27]。

此外，可靠稳定的电网运行除了要求降低DFIG风电系统输出的电流谐波，也需要风电系统输出平稳、可控的有功及无功功率，因此确保谐波电网下DFIG 输出平稳的有功及无功功率也是极具现实意义的控制目标。

本文首先简要叙述了谐波电网下的DFIG 数学模型，解释了谐波电压对DFIG 运行性能的影响。为避免谐波分量提取和转子电流参考值复杂计算导致的控制性能下降，本文针对谐波电网下DFIG 控制提出了一种基于矢量谐振控制的定子电流和定子输出功率集成控制策略，通过加入定子电流或定子有功/无功功率矢量谐振控制以分别实现定子电流无谐波和输出功率无波动。最后，通过构建的DFIG实验机组和谐波电网，对所提控制策略的正确性进行了实验验证。

2 谐波电网电压下DFIG 集成控制策略

考虑到电网电压所含谐波以5 次及7 次分量为主，故本文主要研究电网5 次及7 次谐波电压共存下DFIG 的高性能控制技术。文献[20]已详细推导了5 次、7 次谐波下的DFIG 数学模型，本文仅对谐波电网下DFIG 的数学模型作简单说明。

2.1 谐波电网下DFIG 数学模型

图1 为定子两相静止αβ 坐标系、转子两相相对转子绕组静止αβr坐标系，基频同步旋转dq+坐标系，5 次谐波旋转dq5-坐标系和7 次谐波旋转dq7+坐标系的空间示意图。DFIG 在dq+坐标系下的等效电路如图 2 所示，可以得出矢量控制技术下控制对象DFIG 的传递函数为

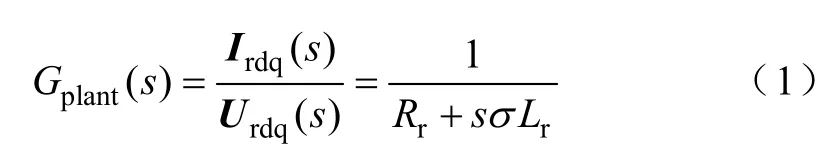
式中 I——电流；

U——电压；

Lr——转子 电感；

Rr——转子 电阻；

下标rdq 为转子dq 轴分量；

σ——漏磁系数，σ=1-L2m/LsLr；

Ls——定子 电 感；

Lm——定转子互感。

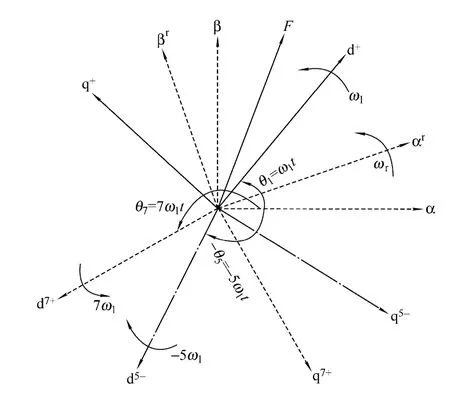
图1 αβ，αβr，dq+，dq5-和dq7+坐标系关系图Fig.1 Spatial relationships between αβ,αβr,dq+,dq5- and dq7+ reference frames

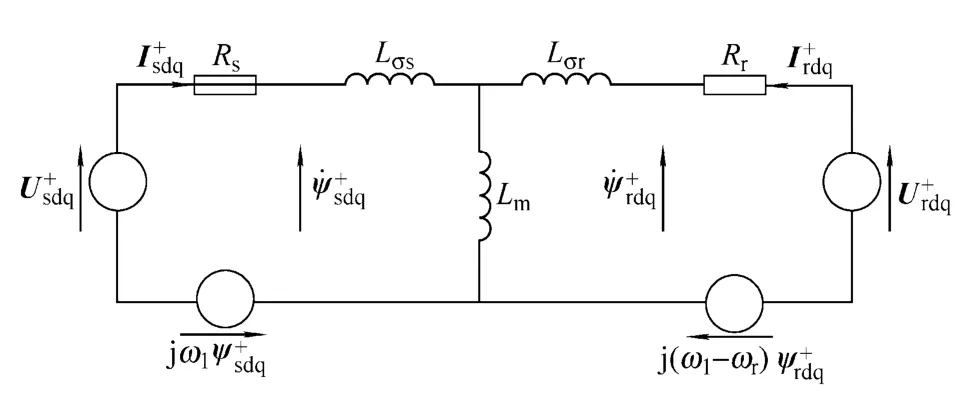
图2 DFIG 在dq+坐标系下的T 形等效电路Fig.2 T-representation of the DFIG equivalent circuit in dq+ reference frame

DFIG 定子电流在dq+坐标系下可表示为

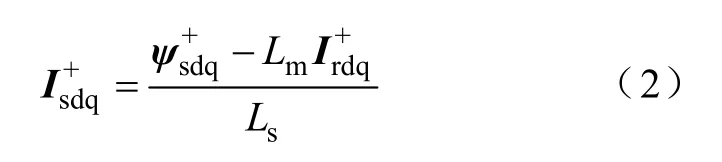
式中 ψ——磁链；

上标+代表dq+旋转坐标系；

下标sdq 为定子dq 轴分量。

DFIG 定子电压在dq+坐标系下可表示为

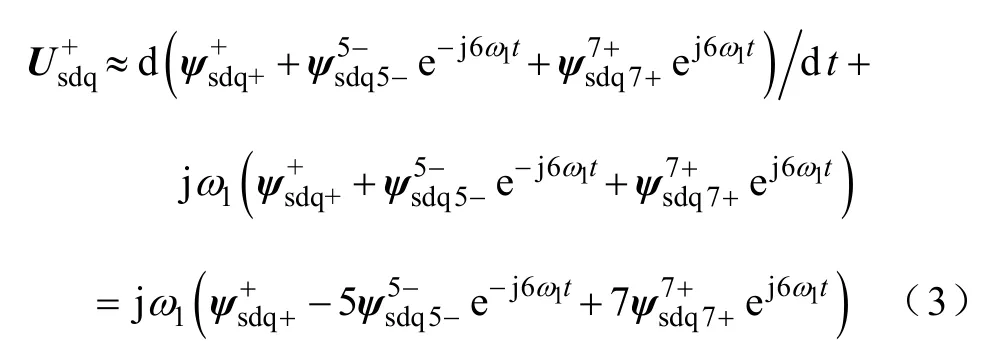
式中 ω1——电网基频角速度；

t——时间；

上标5-，7+分别表示dq5-坐标系和dq7+坐标系；

下标+，5-，7+分别表示基频分量和5 次、7 次谐波分量。

谐波电网电压下DFIG 定子输出瞬时有功和无功功率可表示为

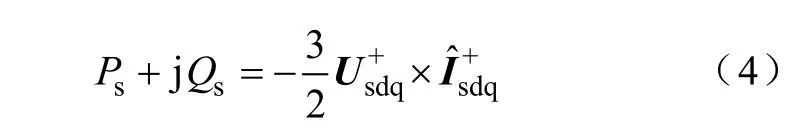
将式（2）、式（3）代入式（4），瞬时有功功率和无功功率可表示为

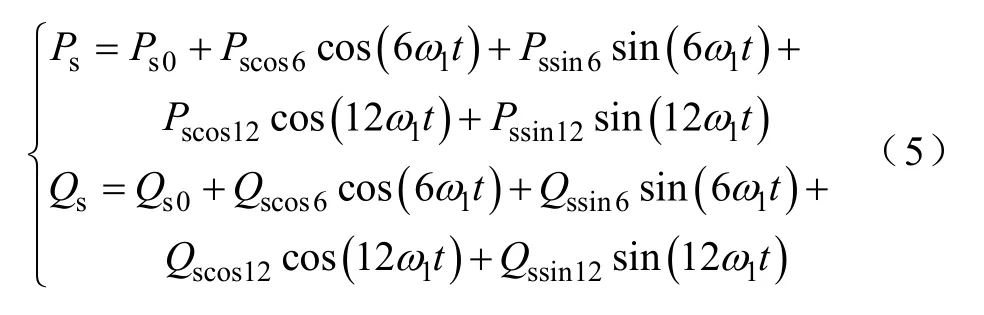
式中，Ps0，Qs0分别为定子有功/无功功率的直流分量；Pscos6，Pssin6，Qscos6，Qssin6分别为定子有功/无功功率的正余弦6 倍频波动分量；Pscos12，Pssin12，Qscos12，Qssin12分别为定子有功/无功功率的正余弦12 倍频波动分量。

定子有功功率及无功功率的6 倍频波动分量由电压电流的基频分量与5 次、7 次谐波分量之间相互作用而产生，12 倍频波动分量由5 次与7 次谐波分量之间相互作用而产生。

从式（5）可以看出，当考虑电网电压5 次，7次谐波分量时，DFIG 定子输出有功/无功功率由直流分量、6 倍频和12 倍频波动分量组成，这对风电机组的大规模并网发电和长时间可靠运行均有不利影响。需要指出的是，由于12 倍频分量由电网电压及定转子电流中含量较小的5 次、7 次谐波分量之间相互作用而产生，因此在实际系统中可以忽略12倍频所造成的不利影响，而主要考虑由基频与5 次、7 次分量之间相互作用而产生的6 倍频波动分量。

2.2 谐波电网下DFIG 的传统控制技术

谐波电网下DFIG 的传统控制技术需要将电网电压中的基频、5 次及7 次谐波分量进行分解提取，并根据DFIG 数学模型，计算得到在不同谐波控制目标下的转子电流5 次及7 次谐波分量参考值，进而通过对转子电流基频及谐波分量的有效调节，达到预定的谐波控制目标[20]。

然而，在上述传统控制技术中，存在以下两点必不可少的计算步骤。

2.2.1 基频及谐波电压分量提取

文献[12,19,20]采取的矢量控制中由于控制器所调节的对象为转子电流，因此为实现不同的谐波控制目标，需首先对电网电压谐波分量进行提取。图3 所示为电网电压基频及谐波分量提取框图，可以看出，输入信号为电网电压在两相静止αβ 坐标系下的分量，经由坐标旋转、陷波器及低通滤波器等环节，可得基频及各次谐波分量检测结果。

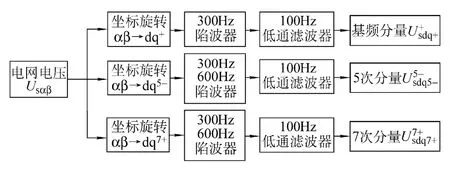
图3 电网电压基频及谐波分量提取框图Fig.3 Grid voltage fundamental and harmonic components extraction block diagram

然而，上述的谐波分量提取环节在实际中有如下缺陷:①坐标旋转依赖于准确电网电压锁相环的输出信号，因此在实际运行中易受电网谐波、负序、相位突变等影响；②陷波器运算复杂，且其输出包含高频干扰信号，从而降低了谐波分量的检测精度；③低通滤波器的引入在滤除高频干扰信号的同时还将对谐波分量造成一定的幅值衰减及相位延迟，难以实现谐波分量的快速准确检测。

2.2.2 转子电流参考值计算

文献[20,22,23]给出的根据不同控制目标的转子电流参考值计算，与电网电压中的5 次及7 次谐波分量，电机参数等等有关，且计算过程复杂耗时，不利于DFIG 的快速准确控制。此外，值得注意的是，转子电流参考值计算与电机参数有关，若DFIG在运行过程中受到诸如温度、磁场、绝缘等条件的影响而发生电机参数偏移时，则相应的转子电流参考值计算中将会引入不可避免的误差，从而降低谐波控制目标达成的精度，不利于DFIG 在谐波电网下的稳定可靠运行。

2.3 DFIG 集成控制策略

为避免谐波分量提取环节所引入的控制误差，以及转子电流参考值计算所引入的参考值误差及计算延时，消除不利于谐波电网下DFIG 系统快速稳定运行的因素，本文提出了改进的DFIG 谐波控制策略，在传统矢量控制策略中转子电流PI 闭环控制的基础上，加入了针对定子电流或者定子功率的矢量谐振调节环节，以达到谐波电压下DFIG 定子电流正弦或输出功率无波动的控制目标。

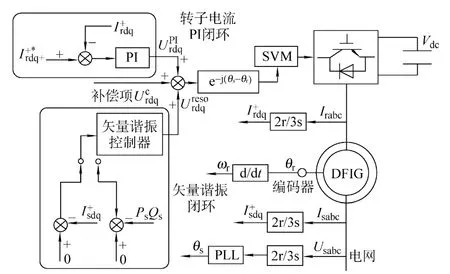
图4 谐波电网下DFIG 集成控制策略框图Fig.4 Block diagram of integrated control strategy for DFIG under harmonic grid

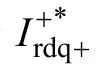
由图4 可知，本文所提控制策略通过集成定子电流与定子功率的闭环控制，并使用矢量谐振控制器以达到消除定子电流谐波分量或者定子功率波动分量的谐波控制目标。集成的矢量谐振闭环控制器反馈值为实际采样定子电流或者由式（4）计算得到的实际定子有功、无功功率。由于控制目标为消除定子电流中的5 次、7 次谐波分量（在同步速旋转坐标系下表现为300Hz 交流分量），或消除定子功率中的300Hz 波动量，因此闭环控制器的参考值为0。考虑到矢量谐振控制器的输入误差信号中均包含直流误差分量及300Hz 交流误差分量，由于矢量谐振控制器仅对300Hz 交流分量有调节能力，而对直流分量不具有调节能力，因此定子电流或者定子功率误差信号中的直流分量不会对300Hz 分量的调节造成影响。这一特性使得所提控制策略不需要对定子电流或者定子功率中的 300Hz 交流分量进行提取，从而有利于谐波控制目标的快速实现。

相比于传统控制策略，本文所提出的集成控制策略有以下优势:

（1）无需转子电流参考值计算，节省计算时间，有利于控制系统的快速响应。

（2）无需电网电压基频及谐波分量提取，大量的坐标旋转，陷波器及低通滤波器都可被移除，软件算法复杂程度得以降低。

（3）由于直接对定子电流或者定子功率进行谐振调节，系统鲁棒性强，对电机参数偏移和电网谐波状态变化不敏感。

由图4 可知，最终用于PWM 调制的转子电压参考值可表示为

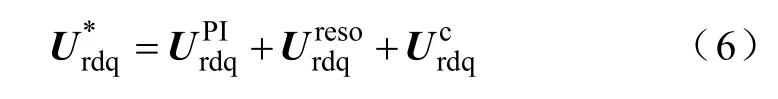
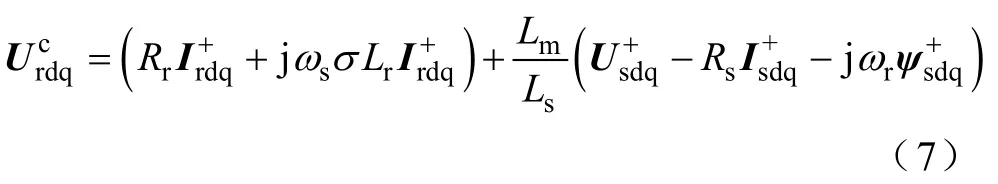
2.4 矢量谐振控制器及稳定性分析

针对谐波电网下DFIG 不同控制目标，本文采用矢量谐振控制器以实现定子电流谐波分量和定子功率波动分量的有效消除。式（8a）、（8b）给出了普通及矢量谐振控制器的传递函数

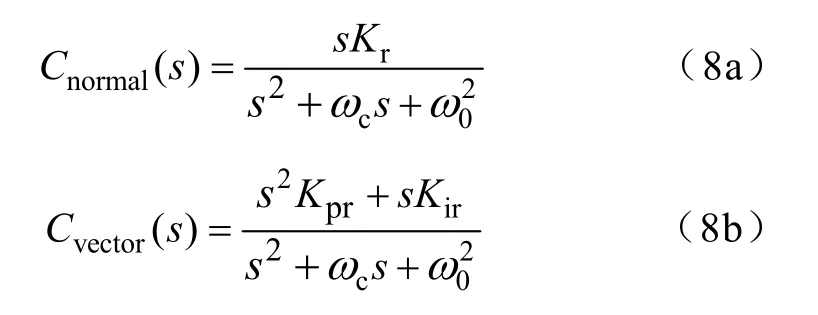
式中，Kr为普通谐振控制器增益参数；Kpr和Kir为矢量谐振控制器增益参数；ωc为谐振频率点处的带宽；ω0为谐振频率。

图4 控制框图中，定子电流闭环输入误差信号包含定子电流基频及谐波分量，在dq+坐标系下表现为直流量及300Hz 交流量，而定子功率闭环输入误差信号包含直流量及300Hz 波动分量。因此，不论矢量谐振闭环所控制的对象为定子电流或定子功率，其输入的误差信号均为直流量及300Hz 交流量。

因此，通过传递函数式（8b），可以得到矢量谐振控制器在频率为0 和300Hz 时的增益为

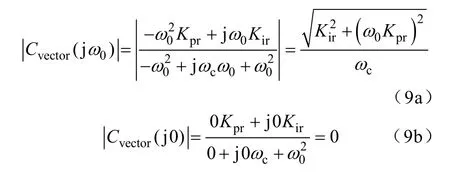
从式（9a）可以看出，矢量谐振器能在谐振频率处产生较高的幅值增益，从而达到对电流和功率谐波分量进行有效控制。从式（9b）可以看出，矢量谐振器对于直流信号的幅值增益为0，对直流分量不具有调节能力，因此矢量谐振控制器输出信号中不包含直流信号。故而，由于矢量谐振闭环仅对闭环控制系统中的谐波分量具有良好的调节能力，定子电流闭环或者定子功率闭环的控制误差中的直流分量不会影响谐波控制目标的实现，从而确保谐波控制目标的快速准确实现。

考虑到DFIG 作为惯性环节会对控制闭环造成一定的相位延迟，为了确保整个闭环系统的稳定工作，需要分析谐波控制下的DFIG 系统开环传递函数。根据式（1）及式（8），可知采用普通、矢量谐振控制器的DFIG 开环传递函数分别为

图5 为采用普通和矢量谐振控制器的开环系统波特图，其中谐振角频率ω0=600πrad/s，DFIG 参数Rr=0.88Ω，转子电感Lr=93mH，漏磁系数σ=0.063，普通谐振控制器参数 Kr=10 000，矢量谐振控制器Kpr=5，Kir=785（由文献[26]可知，可设置Kir=KprRr/σLr以达到零极点相消的目的），两个谐振器带宽参数ωc=30rad/s。由图5a 可以看出，当采用不同的谐振控制器时，其开环传递函数在谐振频率300Hz 处的幅值增益均约为30dB 及29.5dB，表明两者在谐振频率点均具有较强的调节能力。但两个谐振控制器在谐振频率点处表现出不同的相位响应，采用普通谐振器的开环传递函数在谐振频率300Hz 处的相位响应为-85.1°，且在谐振频率点附近，最大相位延迟接近-180°，已接近于闭环系统稳定工作的相位极限，系统易发生不稳定工作。而采取矢量谐振控制器的开环传递函数在谐振频率点处的相位响应为0°，在谐振频率附近处最大相位响应在-90°左右，闭环控制响应具有接近 90°的相位裕度，可确保DFIG 闭环系统的稳定性。

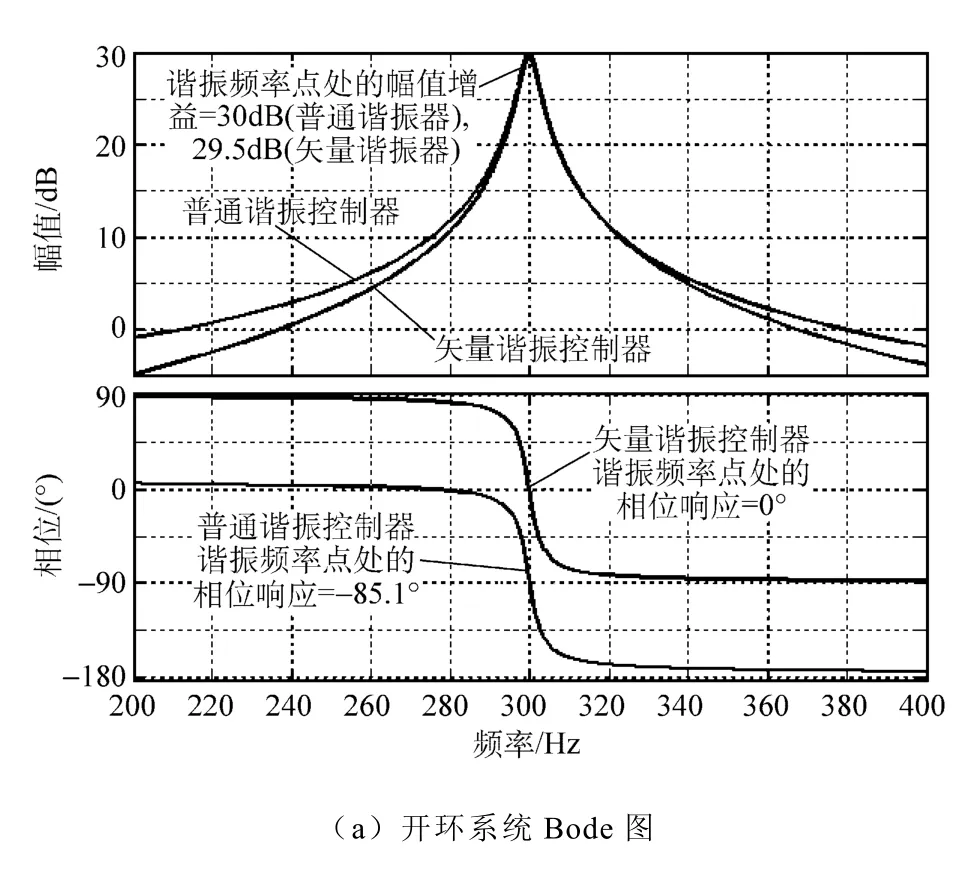
图5 采用普通和矢量谐振控制器的开环系统Bode 图Fig.5 Open-loop Bode diagram using normal and vector resonant regulator

2.5 电网频率波动的影响

此外，我国电网规范中允许电网频率发生±(0.2～0.5)Hz 的频率偏移，考虑到待调节的谐波分量在同步旋转坐标系下为6 倍电网基频分量，该分量频率偏移范围为±(1.2～3)Hz，本文以最恶劣的情况,即在谐振频率300Hz 点处发生频率偏移±3Hz 为例，分析当电网频率发生偏移时所提矢量谐振控制器对于DFIG 中谐波分量的控制能力。

将图5a 中显示的开环系统波特图放大，如图5b 所示，其显示频率范围为297～303Hz。由图5b可以看出，当电网频率发生偏移时，由于谐振频率带宽参数ωc=30rad/s，使得普通谐振器与矢量谐振器分别出现由30～26.0dB，以及由29.5～25.5dB 的幅值增益减小。矢量谐振器所减小的4.0dB 幅值增益依然足以实现300Hz 处误差信号的有效控制，因而ωc的引入增强了谐振控制器在实际电网运行情况下对电网频率偏移的鲁棒性，确保了DFIG 在实际谐波电网条件下运行性能的平稳。

2.6 控制策略的稳态控制精度分析

为确保DFIG 闭环控制的响应精度，需分析谐波控制下DFIG 闭环系统传递函数在谐振频率点处的幅值与相位响应。根据开环传递函数式（10），可以得出普通和矢量谐振控制器下DFIG 闭环传递函数表示为

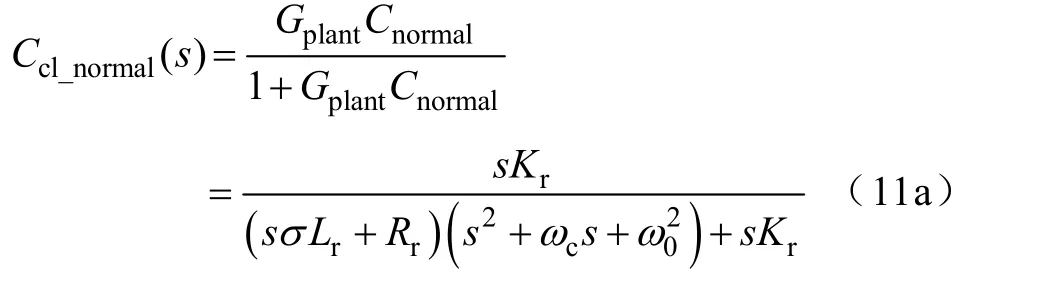
图6 为采用普通和矢量谐振控制器的闭环系统波特图，所采用的参数与图5 相同。由图6a 可以看出，当采用两种不同谐振控制器时，闭环传递函数在谐振频率300Hz 处的幅值响应分别为-0.03dB（普通谐振器），-0.28dB（矢量谐振器），可确保实际信号与给定信号在幅值上保持一致。但两者表现出不同的相位响应，当采用矢量谐振控制器时，闭环传递函数在谐振频率300Hz 点处的相位响应为0°，可确保实际的待调节定子电流谐波分量或者定子功率脉动分量能与给定值不仅在幅值上保持相等，同时也能实现相位的准确同步。但是若采用普通谐振控制器时，在谐振频率点处的相位响为-1.8°，无法实现相位上的一致性，从而降低谐波控制目标的实现精度。

图6 采用普通和矢量谐振控制器的闭环系统Bode 图Fig.6 Closed-loop Bode diagram using normal and vector resonant regulator

还需要指出的是，通过把图6a 中显示的闭环系统波特图放大，如图6b 所示，其频率范围为297～303Hz。可以看出，当电网频率发生偏移时，矢量谐振器可保持恒定的闭环幅值响应，表明电网频率偏移发生时系统的闭环控制响应保持不变。而采用普通谐振控制器时，在300Hz 处的频率偏移±3Hz将造成闭环幅值响应变化0.68dB，进而不利于DFIG在实际电网条件下达到平稳的稳态控制精度。

2.7 DFIG 参数变化的影响

在实际工程应用过程中，由于电机气隙磁场饱和，温升及绝缘等条件的影响，DFIG 参数将在一定程度内发生偏移，因此需要进一步研究DFIG 参数偏移对所提控制策略的影响。

由式（1）可知，控制对象DFIG 传递函数中所包括的电机参数有转子电阻 Rr以及漏磁系数和转子电感的乘积σLr。由于谐振频率为600πrad/s，此时sσLr>>Rr，因此本文对DFIG 参数偏移的讨论仅关注 σLr发生偏移的情况，其偏移范围设定为±20%[28]。

图7 DFIG 参数偏移时采用矢量谐振控制器的开环系统Bode 图Fig.7 Open-loop Bode diagram using vector resonant regulator when DFIG parameters deviation happens

图7 给出了当DFIG 参数σLr发生±20%偏移时的采用矢量谐振控制器的控制系统开环传递函数波特图，所采用的参数与图5 相同。可以看出，当DFIG参数σLr发生-20%偏移时，采用矢量谐振控制器的开环系统在300Hz 谐振频率点处的幅值响应由原本的29.5dB 略微增大至31.0dB。而当DFIG 参数σLr发生+20%偏移时，谐振频率处的幅值响应略微减小至27.5dB。上述在27.5～31.0dB 之间的开环传递函数谐振频率点处的幅值响应均能确保足够大的增益，以确保准确抑制控制误差，满足控制精度要求。此外，当DFIG 参数发生变化时，开环传递函数在谐振频率点处的相位响应几乎保持不变，均接近0°，从而确保不会对300Hz 交流控制误差信号造成相位超前或滞后，有助于提高控制精度。

图8 给出了当DFIG 参数σLr发生±20%偏移时的采用矢量谐振控制器的控制系统闭环传递函数Bode 图，所采用的参数与图5 相同。可以看出，当DFIG 参数σLr发生-20%偏移时，采用矢量谐振控制器的闭环系统在300Hz 谐振频率点处的幅值响应由原本的-0.30dB 略微增大至-0.23dB。而当DFIG 参数σLr发生+20%偏移时，谐振频率处的幅值响应略微减小至-0.38dB。由此可知，DFIG 参数变化不会对采用矢量谐振控制器的闭环传递函数幅值响应造成影响，系统依然能够确保较高的控制精度，有利于控制目标的达成。此外，当DFIG 参数发生变化时，闭环传递函数在谐振频率点处的相位响应保持不变0°，从而确保不会对300Hz 交流控制误差信号造成相位超前或滞后。

图8 DFIG 参数偏移时采用矢量谐振控制器的闭环系统Bode 图Fig.8 Closed-loop Bode diagram using vector resonant regulator when DFIG parameters deviation happens

分析可见，采用矢量谐振控制器的控制系统开环传递函数及闭环传递函数对于DFIG 参数偏移具有较强的鲁棒性，确保了控制系统在DFIG 参数偏移的实际条件下的可靠稳定运行。

由上述讨论可知，相比于普通谐振控制器而言，采用矢量谐振控制器的闭环调节能够确保在300Hz谐振频率点处的0dB 幅值响应以及0°的相位响应，因此具有更为优秀的闭环控制精度。且采用矢量谐振控制器的闭环控制能够确保在谐振频率点附近的频率范围内的相位裕度均接近于90°，从而确保了闭环控制系统的工作稳定性。此外，由于谐振带宽参数ωc的引入使得矢量谐振器的幅值响应能在谐振频率300Hz 附近基本保持不变，从而在电网频率发生偏移时仍然确保良好的谐波控制能力，实现DFIG 在实际谐波电网条件下的稳定可靠运行。且当DFIG 参数发生变化时，采用矢量谐振控制器的闭环传递函数能够使得在谐振频率点处的幅值与相位响应保持不变，表现出较强的鲁棒性。

3 系统构建

为了实验验证所提控制策略在谐波电网电压条件下的可行性和有效性，构建了DFIG 转子侧变流器系统及谐波电网模拟装置，实验平台系统框图如图9 所示。其中用于模拟风力机的笼型异步电机由通用变频器拖动，并与DFIG 同轴相连。由于主要验证转子侧变流器的控制策略，故未在DFIG 系统中考虑网侧变流器。转子侧变流器直流母线电压由直流电源提供，谐波电网模拟装置由三相电压源型逆变器组成，用于调节所需谐波的阶次及幅值等。

图9 实验平台系统框图Fig.9 Schematic diagram of the experiment system

表1 给出了实验用DFIG 电机参数，谐波控制算法的实现基于TI 公司的DSP TMS320F2812，采样频率为10kHz，转子侧变流器采用SVPWM 调制，IGBT 开关频率设定为 5kHz。实验波形由横河的DL750 录波仪采集，谐波含量分析由Fluke 的Norma 5000 功率分析仪完成。

表1 DFIG 及系统参数Tab.1 Parameter of the experiment DFIG system

4 实验验证

基于构建的DFIG 系统及谐波电网发生装置，进行了谐波电网电压下（考虑5 次、7 次谐波电压分量），以定子电流正弦或者定子输出有功/无功功率无波动为控制目标的实验研究。需要指出的是，由于电机本身存在齿谐波及饱和等因素影响，使得实验过程中DFIG 定转子电流中均存在非预期的谐波分量，可将这些谐波分量看做为背景谐波，则有助于关注本文所讨论的5 次、7 次谐波下的DFIG控制策略的有效性。并且在整个实验过程中，DFIG被拖动至800r/min（0.8pu），定子向电网发出有功功率400W 及无功功率0var。

图10 理想电网下DFIG 系统实验结果Fig.10 Experiment results of DFIG system under ideal grid conditions

图10 给出了运行于理想电网的DFIG 系统实验结果。可以看出，当电网理想时，电网电压中仍然分别包含有0.80%的5 次及0.44%的7 次谐波分量。此时DFIG 定子电流包含轻微的畸变，即3.87%的5次及1.45%的7 次谐波分量，而定子输出有功功率及无功功率基本保持稳定。而由于电机转子转速为0.8(pu)（40Hz），其与5 次、7 次谐波分量相互作用将会在转子绕组中感应出290Hz（250Hz+40Hz）及310Hz（350Hz-40Hz）的转子电流谐波分量。排除由齿谐波及饱和等因素导致的定转子电流非预期谐波分量及其所产生的功率波动，通过对5 次、7 次电网电压、定转子电流及相应的定子功率波形进行频谱分析，可得表2 所示的分析结果。

表2 DFIG 系统响应对比Tab.2 DFIG system response comparison

图11 给出了谐波电网下DFIG 采用无谐波控制策略的运行实验结果。由图11 可见，当电网电压中出现THD 接近5%的5 次、7 次谐波分量，而无有效谐波控制策略时，DFIG 定转子电流将出现严重畸变，即对于定子电流而言，13.39%的 250Hz 及8.59%的350Hz 谐波分量；对转子电流而言，6.56%的290Hz 及4.29%的310Hz 谐波分量。此外，定子输出有功/无功功率也均包含明显的300Hz 脉动，分别为±30W 及±30var。

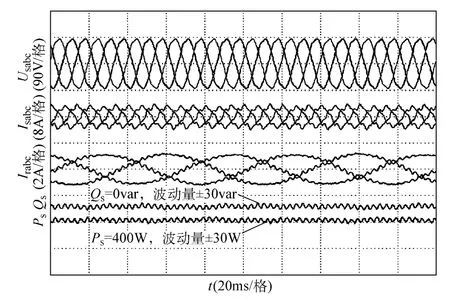
图11 谐波电网下无谐波控制策略的DFIG 系统实验结果Fig.11 Experiment results of DFIG system under distorted grid conditions without harmonic control strategy

图12 给出了在谐波电网下定子电流闭环控制使能条件下的DFIG 运行性能实验结果。通过对比图11 和图12，可以看出电机定子电流波形得到显著改善，排除由齿谐波及饱和等因素导致的定子电流非预期谐波分量，其中定子电流250Hz 分量由图11 中的13.39%降低至1.53%，350Hz 分量由8.59%下降至1.30%。此外，定子有功/无功功率的300Hz波动分量也有所抑制，由图11 中的±30W 及±30var降低至图12 中的±10W 及±5var，从而证明了定子电流谐振控制的有效性。

图12 谐波电网下采取定子电流谐振控制策略的DFIG 系统实验结果Fig.12 Experiment results of DFIG system under distorted grid conditions with stator current resonant control loop enabled

图13 给出了在谐波电网下定子功率谐振闭环控制使能时的DFIG 运行性能实验结果。通过对比图11 和图13，可以看出电机定子有功/无功功率波动得到显著抑制，排除由齿谐波及饱和等因素导致的定转子电流非预期谐波分量及其所产生的功率波动，其中定子有功功率波动分量由图11 中的±30W降低至图13 中的±3W；定子无功功率波动分量由图11 中的±30var 降低至图13 中的±3var。但是需要指出的是，对比图12 与图13 可知，图13 中的定子有功/无功功率被良好抑制的同时，定子电流的谐波含量相比图12 有所增加，因此定子电流正弦与定子功率稳定这两个谐波控制目标是相互冲突而无法同时实现的。

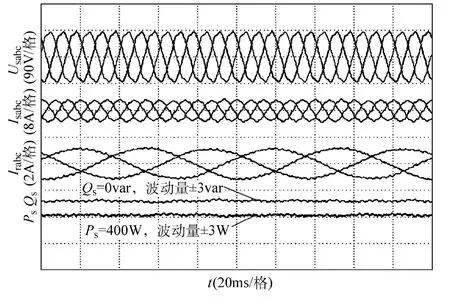
图13 谐波电网下采取定子功率谐振控制策略的DFIG 系统实验结果Fig.13 Experiment results of DFIG system under distorted grid conditions with stator power resonant control loop enabled

图14 给出了在两种谐波控制目标切换瞬间的DFIG 运行实验结果。可以看出，在切换时间点前后，系统均能良好实现各自的谐波控制目标，仅在切换时间点之后的 100ms 内有一定的过渡过程出现，随即成功由定子电流正弦目标切换为定子功率平稳目标。

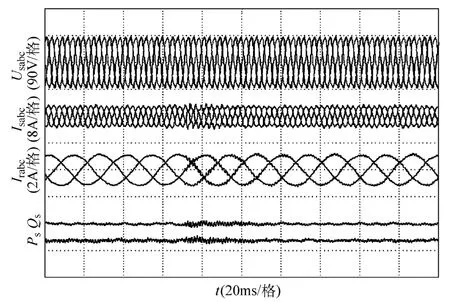
图14 定子电流/功率谐振切换时DFIG 系统实验结果Fig.14 Experiment results of DFIG system at the time of switching stator current/power resonant control

图15 给出了当定子电流正弦谐振控制策略使能情况下，电机定子有功功率由300W 阶跃至500W的DFIG 运行实验结果。由图可见，在整个系统瞬态过程期间，定子电流谐振闭环的有效调节使得定子电流在过渡过程中能够仍然保持正弦，并且定子电流幅值增大过程中没有超调量出现，也即证明了转子电流PI 闭环与定子电流谐振闭环工作的相互独立性。

图15 定子有功功率阶跃时DFIG 系统实验结果Fig.15 Experiment results of DFIG system at the time of stator active power stepping

图16 给出了当定子电流正弦谐振控制策略使能情况下，电网电压由理想状态突变为谐波电网时的DFIG 运行实验结果。由图16 可见，在切换点之前，由于电网理想，因此定子电流接近正弦；而当电网谐波分量出现瞬间，定子电流及转子电流出现明显畸变。约40ms 之后，在定子电流谐振闭环的有效工作下，定子电流仍然能够恢复至接近理想状态下的响应，从而证明了所提出的定子电流谐振闭环的快速性及有效性。

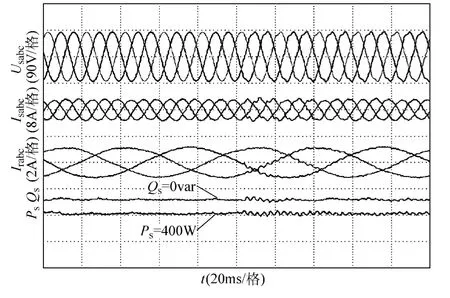
图16 保持定子电流正弦，电网电压有/无谐波分量切换时DFIG 系统实验结果Fig.16 Experiment results of DFIG system at the time of existing grid voltage harmonic component or not with the control target of sinusoidal stator current

5 结论

为实现DFIG 在谐波电网下的高性能运行，本文提出了以DFIG 定子电流正弦或定子输出有功/无功功率平稳为谐波控制目标，在转子电流PI调节基础上采用基于矢量谐振的定子电流或定子功率的闭环控制，以消除定子电流中的谐波或者定子输出功率的波动，改善DFIG 在谐波电网下的运行性能。

（1）相比较传统控制策略，本文所提策略不需要对电网电压及转子电流进行谐波分量提取，不需要进行转子电流参考值计算，节省DSP 计算时间，有利于DFIG 闭环控制响应的快速性及稳定性；

（2）本文所采用的矢量谐振控制器相比于普通谐振控制器，具有优越的闭环控制稳定性及交流信号调节能力，且对于电网频率偏移以及DFIG 参数偏移均具有较强的鲁棒性，确保了在实际电网和电机条件下谐波控制目标的准确实现。

实验结果表明，所提的谐波控制策略可有效抑制定子电流中的谐波或定子功率波动，验证了本文所提谐波控制策略的正确性。

[1]刘其辉,贺益康,张建华.交流励磁变速恒频双馈型异步发电机的稳态功率关系[J].电工技术学报,2006,21(2):39-44.Liu Qihui,He Yikang,Zhang Jianhua.Steady-state power relation of AC-excited variable-speed constantfrequency doubly-fed induction generator[J].Transactions of China Electrotechnical Society,2006,21(2):39-44.

[2]刘其辉,谢孟丽.双馈式变速恒频风力发电机的空载及负载并网策略[J].电工技术学报,2012,27(10):60-67.Liu Qihui,Xie Mengli.Strategies of grid-connection of doubly-fed variable-speed constant-frequency wind power generator with no-load and with load[J].Transactions of China Electrotechnical Society,2012,27(10):60-67.

[3]刘其辉,贺益康,张建华.交流励磁变速恒频风力发电机的运行控制与建模仿真[J].中国电机工程学报,2006,26(5):43-50.Liu Qihui,He Yikang,Zhang Jianhua.Operation control and modeling-simulation of AC-excited variable-speed constant-frequency (AEVSCF) wind power generator[J].Proceedings of the CSEE,2006,26(5):43-50.

[4]吴国祥,马炜,陈国呈,等.双馈变速恒频风力发电空载并网控制策略[J].电工技术学报,2007,22(7):169-175.Wu Guoxiang,Ma Yiwei,Chen Guocheng,et al.Research on idle load grid-connection control strategy for variable-speed constant-frequency wind power generation[J].Transactions of China Electrotechnical Society,2007,22(7):169-175.

[5]刘其辉,贺益康,赵仁德.交流励磁变速恒频风力发电系统的运行与控制[J].电工技术学报,2008,23(1):129-136.Liu Qihui,He Yikang,Zhao Rende.Operation and control of AC-exited variable-speed constant-frequency wind power generation system [J].Transactions of China Electrotechnical Society,2008,23(1):129-136.

[6]胡家兵,贺益康,郭晓明,等.不平衡电压下双馈异步风力发电系统的建模与控制[J].电力系统自动化,2007,31(14):47-56.Hu Jiabing,He Yikang,Guo Xiaoming,et al.Modeling and control of the DFIG based wind-power generation system under unbalanced grid voltage conditions[J].Automation of Electric Power Systems,2007,31(14):47-56.

[7]胡胜,林新春,康勇,等.一种双馈风力发电机在电网电压不平衡条件下的改进控制策略[J].电工技术学报,2011,26(7):21-29.Hu Sheng,Lin Xinchun,Kang Yong,et al.An improved control strategy of doubly-fed induction generator under grid voltage unbalance[J].Transactions of China Electrotechnical Society,2011,26(7):21-29.

[8]胡家兵,贺益康,王宏胜.不平衡电网电压下双馈感应发电机网侧和转子侧变换器的协同控制[J].中国电机工程学报,2010,30(9):97-104.Hu Jiabing,He Yikang,Wang Hongsheng.Coordinated control of grid-and rotor-side converters of doublyfed induction generator under unbalanced network voltage conditions[J].Proceedings of the CSEE,2010,30(9):97-104.

[9]胡家兵,贺益康,王宏胜.不平衡电网电压下双馈感应发电机转子侧变换器的比例-谐振电流控制策略[J].中国电机工程学报,2010,30(6):48-56.Hu Jiabing,He Yikang,Wang Hongsheng.Proportionalresonant current control scheme for rotor-side converter of doubly-fed induction generators under unbalanced network voltage conditions[J].Proceedings of the CSEE,2010,30(6):48-56.

[10]IEEE,New York.IEEE Standard 519—1992.IEEE recommended practices and requirements for harmonic control in electrical power systems[S].1993.

[11]The Gambica Association Limited,London.Managing harmonics-a guide to ENA engineering recommendation G5/4-1[S].2005.

[12]徐君,陈文杰,徐德鸿,等.电网低次谐波电压下双馈风电系统定子谐波电流抑制[J].电力系统自动化,2011,35(8):87-92.Xu Jun,Chen Wenjie,Xu Dehong,et al.Stator harmonic current suppression strategy for doubly-fed wind power generation system influenced by loworder harmonic voltage of grid[J].Automation of Electric Power Systems,2011,35(8):87-92.

[13]Singh G K.Power system harmonics research:a survey[J].European Transactions on Electrical Power,2007,19(2):151-172.

[14]Emanuel A E.Estimating the effects of harmonic voltage fluctuations on the temperature rise of squirrel-cage motors[J].IEEE Transactions on Energy Conversion,1991,6(1):161-168.

[15]Ramos C J,Martins A P,Carvalho A S.Rotor current controller with voltage harmonics compensation for a DFIG operating under unbalanced and distorted stator voltage[C].The 33rd Annual Conference of the IEEE Industrial Electronics Society (IECON),2007:1287-1292.

[16]徐海亮,胡家兵,贺益康.电网谐波条件下双馈感应风力发电机的建模与控制[J].电力系统自动化,2011,35(11):20-26.Xu Hailiang,Hu Jiabing,He Yikang.Modeling and control of wind turbine driven doubly-fed induction generators under harmonic grid voltage conditions[J].Automation of Electric Power Systems,2011,35(11):20-26.

[17]Van Tung Phan,Hong Hee Lee.Performance enhancement of stand-alone DFIG systems with control of rotor and load side converters using resonant controllers[J].IEEE Transactions on Industry Applications,2012,48(1):199-210.

[18]Yao Jun,Li Hui,Chen Zhe,et al.Enhanced control of a DFIG-based wind-power generation system with series grid-side converter under unbalanced grid voltage conditions[J].IEEE Transactions on Power Electronics,2013,28(7):3167-3181.

[19]Zhang Shao,King Jet Tseng,San Shing Choi,et al.Advanced control of series voltage compensation to enhance wind turbine ride through[J].IEEE Transactions on Power Electronics,2012,27(2):763-772.

[20]Hu Jiabing,Nian Heng,Xu Hailiang,et al.Dynamic modeling and improved control of DFIG under distorted grid voltage conditions[J].IEEE Transactions on Energy Conversion,2011,26(1):163-175.

[21]徐海亮,章玮,胡家兵,等.电网电压不平衡及谐波畸变时基波电压同步信号的检测[J].电力系统自动化,2012,36(5):90-95.Xu Hailiang,Zhang Wei,Hu Jiabing,et al.Synchronizing signal detection of fundamental voltage under unbalanced and/or distorted grid voltage conditions[J].Automation of Electric Power Systems,2012,36(5):90-95.

[22]Xu Hailiang,Hu Jiabing,He Yikang.Operation of wind-turbine-driven DFIG systems under distorted grid voltage conditions:analysis and experimental validations[J].IEEE Transactions on Power Electronics,2012,27(5):2354-2366.

[23]Xu Hailiang,Hu Jiabing,He Yikang.Integrated modeling and enhanced control of DFIG under unbalanced and distorted grid voltage conditions[J].IEEE Transactions on Energy Conversion,2012,27(3):725-736.

[24]Chudamani R,Vasudevan K,Ramalingam C S.Comparative evaluation of harmonic extraction techniques for three-phase three-wire active power filter[C].7th International Conference on Power Electronics and Drive Systems,2007:1700-1706.

[25]Liu Changjin,Blaabjerg Frede,Chen Wenjie,et al.Stator current harmonic control with resonant controller for doubly fed induction generator[J].IEEE Transactions on Power Electronics,2012,27(7):3207-3220.

[26]Lascu Cristian,Asiminoaei Lucian,Boldea Ion,et al.Frequency response analysis of current controllers for selective harmonic compensation in active power filters[J].IEEE Transactions on Industrial Electronics,2009,56(2):337-347.

[27]年珩,宋亦鹏.谐波电网下基于矢量比例积分电流控制器的双馈异步发电机运行控制技术[J].中国电机工程学报,2013,33(6):101-111.Nian Heng,Song Yipeng.DFIG operation control strategy under distorted grid conditions based on VPI current regulators[J].Proceedings of the CSEE,2013,33(6):101-111.

[28]Hany M Jabr,Narayan C Kar.Effects of main and leakage flux saturation on the transient performances of doubly-fed wind driven induction generator[J].Electric Power System Research,2007,77(8):1019-1027.