探求通项公式，证好数列不等式

雷小华

在作答高考数列大题时，许多考生对求数列的通项公式与证明数列不等式感到困难，甚至止步不前.当进入高三第二轮专题复习时，如何较快提高考生分析问题与解决问题的能力而解好这道数列大题呢？

经过查阅近年广东高考理科试题，我发现试题题型趋于稳定，难度、风格变化也不大.其中数列大题越来越接近考生的实际水平，趋于平和.在第二轮专题复习时，若能把数列中的重要内容再收敛聚焦，有的放矢，则在高考作答时解题效率应会有所提高.

鉴于此，我依纲靠本，顺流而下，以《探求通项公式，证好数列不等式》为专题，把本专题共分为3节课，以第1节《探求通项公式》为课题，面向全区高三数学教师上了一堂探索公开课.其形式为：题组呈现，评练结合；分析归纳，实践提高.课堂内容大致如下：

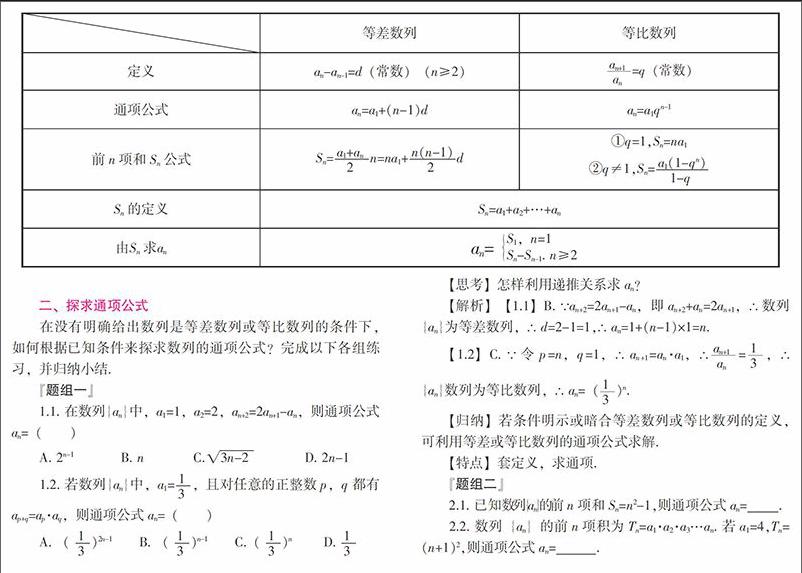
一、基础知识梳理

课前先由学生梳理一下数列中的基础内容，以备后用.

【思考】①如何削枝叶（a1·a2·a3，…，an-1），突主干（an），驱喽罗（a1，a2，a3，…，an-1），擒大王（an）？②正确表述an应注意什么？

【解析】【2.1】当n=1时，a1=S1=0，当n≥2时，an=Sn-Sn-1=（n2-1）-[（n-1）2-1]=2n-1. ∵ a1=0≠2×1-1，∴an=0，n=1

2n-1. n≥2endprint