定性比较带电粒子在有界磁场中运动时间的方法

邓思平

有界匀强磁场是指只在局部空间存在的匀强磁场.带电粒子垂直磁场方向从磁场边界进入，由于入射速度和磁感应强度的可变性，造成它在磁场中运动的圆弧轨迹各不相同，对应的运动时间也各不相同.

定性比较带电粒子在有界磁场中运动时间的方法有两种.一种是通过比较圆心角的大小来比较时间的长短，适用于磁感应强度不变的情况，其计算公式是t=·T；另一种是通过比较弧长（弦长）的长短来比较时间的长短，适用于速度大小不变的情况，其计算公式是t=.从教学实践来看，由于求解磁场中运动时间的计算题练习量较大，学生运用第一种方法的意识比较到位.而第二种方法往往多用于定性分析，不经常用来定量计算，学生往往重视不够，训练不多，不能形成意识.本文拟就这两种方法的应用范围和选择依据通过实例进行分析，以期帮助读者掌握比较此类运动时间的方法.

一、其它不变，仅入射粒子的速率改变的情况，适用公式t=·T.

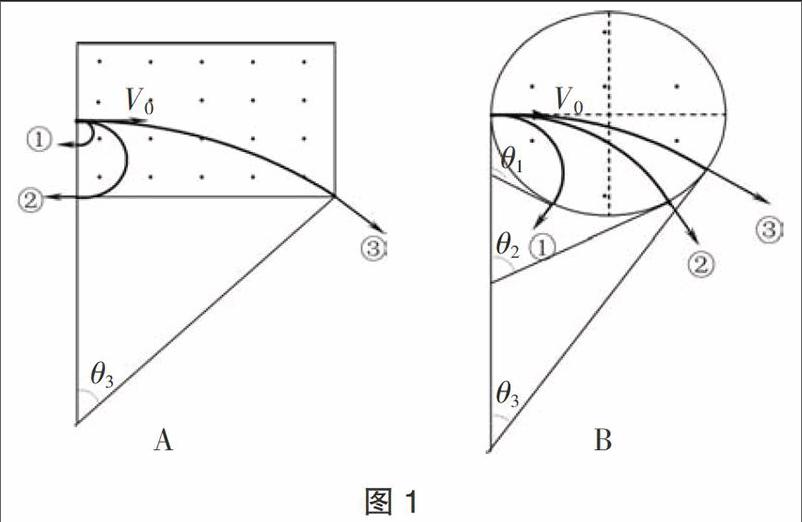
【例1】如图所示圆形区域（图1-A）和矩形区域（图1-B）内，有垂直于纸面方向的匀强磁场，一束质量和带电量都相同的带电粒子，以不相等的速率，沿着相同的方向，垂直边界射入匀强磁场中，又都从该磁场中射出，这些粒子在磁场中的运动时间有的较长，有的较短，若带电粒子在磁场中只受磁场力的作用，试比较三条轨迹①②③对应运动时间的长短.

【解析】同一粒子在匀强磁场中做匀速圆周运动的周期与速率无关，当粒子的速率改变时，周期不变，在磁场中的运动时间t与偏转角度θ（圆心角）成正比，宜用公式t=·T.比较图1-A所示区域中三条轨迹①②③对应的圆心角，发现θ1=θ2=π>θ3，则运动时间t1=t2>t3.比较图1-B所示区域中三条轨迹①②③对应的圆心角，发现θ1>θ2>θ3，则运动时间t1>t2>t3.

二、其它不变，仅磁感应强度B的大小发生变化的情况，适用公式t=.

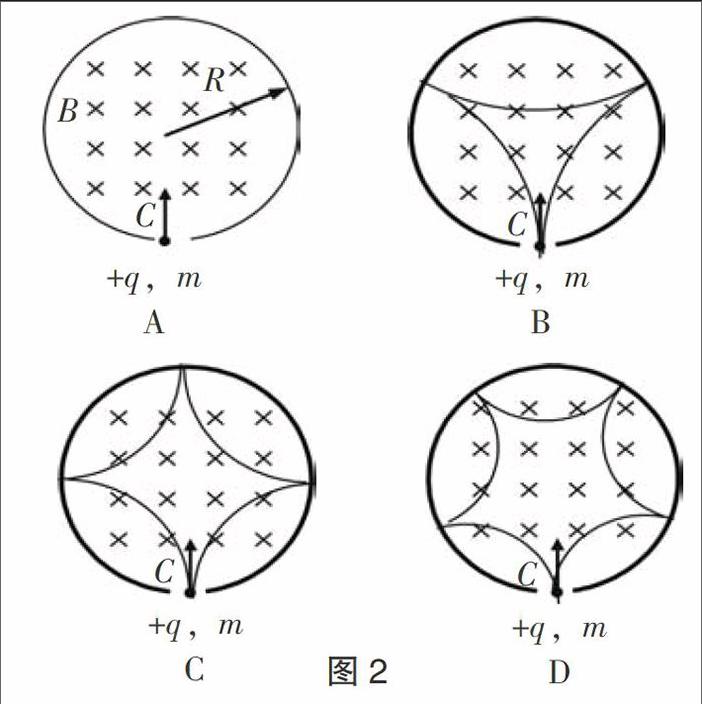
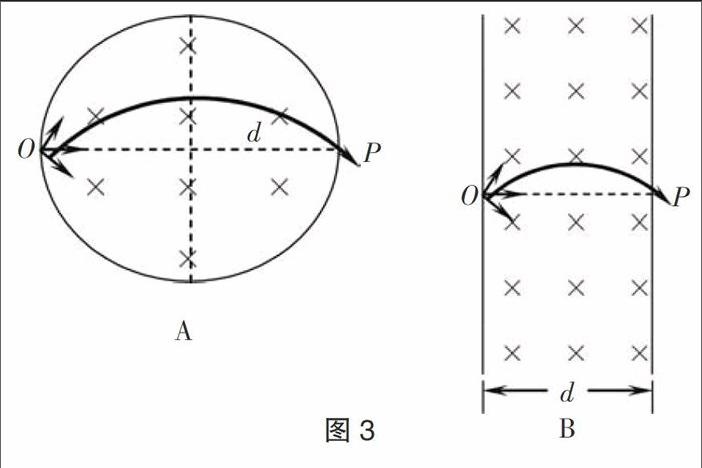
若将例1的条件更改成带电粒子的入射速度相同，且满足前一粒子射出磁场时，后一粒子才进入，每一个粒子进入时的磁场不同.依旧比较三条轨迹①②③对应运动时间的长短时，就会发现，第③条轨迹对应的磁场的磁感应强度B最弱，运动周期T最大，但偏转角度θ最小，公式t=·T已经不能直接用来判断时间的长短.若注意到粒子的入射速度相同，而三条轨迹①②③的长度不同，那么公式t=正适合用来比较运动时间的长短.比较粒子在两个磁场区域中运动时间的结果均为t1

【例2】如图2-A所示在半径为R的绝缘圆筒内有匀强磁场，方向垂直纸面向里，圆筒正下方有一小孔C，一带电量为+q、质量为m的带电粒子（重力忽略不计），以速度v0从小孔C处向着圆心射入磁场.已知带电粒子与筒壁的碰撞无电荷量的损失，且每次碰撞时间极短，碰后以原速率返回.若施加的磁感应强度B合适时，此粒子能在最短的时间内从小孔C处射出，求粒子与筒壁的碰撞次数.

【解析】初看这道题，涉及到时间，很多学生自然地想到了周期公式T=，认为B越大，则T越小，从而认为B越大越好.殊不知，B越大时，根据r=，带电粒子运动的轨道半径也将越小，这就意味着带电粒子与筒内壁碰撞次数将增多，情形如图B、C、D所示

从几何知识容易得到，碰撞的最小次数必须是3次.碰撞次数越多，则轨道半径r越小，带电粒子的轨迹长度也将越长，所以图2-B所示的带电粒子的轨迹长度即三段弧长总和s最短；而粒子在运动过程中，速率不变，从而根据公式t=，得到时间t必然最短.

三、其它不变，仅粒子入射方向可以任意的情况，适用公式t=.

【例3】如图所示圆形区域（图3-A）和条形区域（图3-B）内，有垂直于纸面方向的匀强磁场，一束电子（电荷量为-e，质量为m）自点O以速率v射入磁感应强度为B的匀强磁场中，圆形区域的半径为d，条形区域的宽度也为d.已知d<，带电粒子在磁场中只受磁场力的作用.由于电子入射方向不同，穿过磁场所用时间不同，求

①用最长时间穿过圆形磁场区域的粒子的出射位置；

②以最短时间穿过条形磁场区域的粒子的出射位置.

【解析】由于电子运动速率相同，则不同方向射入的电子的运动半径相同，由几何知识可知，轨迹弧均为劣弧，弧长与弦长成正比.在图3-A中，弦OP最长，对应弧长也最长，由t=可知时间最长.在图3-B中，弦OP最短，对应弧长也最短，由t=可知时间最短.

本题也可用比较圆心角的方法来判断，但较为繁琐.

四、结论

从以上列举的三种情况及相关实例的解析来看，比较带电粒子在有界匀强磁场中的运动时间时，要依据具体情况选择判断公式.总之，定性比较磁场中运动时间时，若入射速率相同，优先选用公式t=；若入射速率不同，只能选用公式t=·T.

（作者单位：梅州市梅县区高级中学）

责任编校 李平安