基于DDA和FDTD算法的银纳米球及其阵列LSPR现象分析
2014-11-23张晓锋
张晓锋,周 伟
0 引言
贵金属纳米颗粒(金或者银)等在入射光照下,如果入射光子频率与贵金属纳米颗粒传导电子的整体振动频率相匹配,纳米颗粒或金属岛会对光子能量产生很强的吸收作用,就会发生局域表面等离子体共振(localize surface plasmon resonance,LSPR)现象。这种现象从18世纪法拉第研究胶体金开始被发现[1]。1908年,Mie提出了解释LSPR现象的Mie理论[2]。目前,基于LSPR现象的传感器被广泛研究,用于药物检测、生物检测、细胞标记、定点诊断、分子动力学研究及疾病诊断等方面。这种传感器具有无需标记、实时、无污染、高灵敏度检测及所需样液少等优点。Mie理论简单实用,能很好地解决球形纳米颗粒的消光(分别包括吸收和散射)问题,但是不能解决复杂形状的颗粒以及颗粒之间的互相耦合作用及基底对纳米颗粒消光特性的影响问题。为此,各种数值计算理论和方法相继产生,如有限元法(finite elementmethod,FEM)[3]、严格耦合波近似理论(rigorous coupled-wave analysis,RCWA)[4]、离散偶极近似法(discrete dipole approximation,DDA)[5]和时域有限差分法(finite difference time domain,FDTD)[6]等。本文主要采用DDA及FDTD算法对银纳米球及其阵列进行分析,所得结论具有重要的参考价值。
1 DDA与FDTD方法的比较
DDA和FDTD是对LSPR进行理论分析应用最多的研究方法[7]。
DDA方法最初是由Devoe[8]提出,用于分析分子聚合体的光学特性,经过逐步的发展与完善而成为一种研究纳米光学现象的有力工具。到目前为止,已经有大量的文献详细讨论了DDA的原理及其应用[7,9-10]。Draine等人在DDA方法的基础上应用快速傅里叶变换和离散共轭梯度的方法,制作了开源软件DDSCAT。DDSCAT可以将各种不同形状、不同材质的纳米颗粒离散成偶极子,计算其消光效率(Q_ext)、吸收效率(Q_abs)、散射效率(Q_sca),其中,Q_ext=Q_abs+Q_sca。不仅可以计算在单一频率下的纳米颗粒的消光情况,而且可将一连续的光谱分为各个不同的点来计算纳米颗粒在连续频谱下的消光现象。此软件不仅适用于单个纳米颗粒,对周期排列的纳米颗粒阵列也同样适用。缺点是对于不是软件自有形状的颗粒需要重新编程建模,建模的过程不是可视化的,需要对输出结果进行再处理才能描绘颗粒表面的电场分布情况。
FDTD方法最早是由Kane SYee在1966年提出的[11],用变量离散的含有有限个未知数的差分方程近似地替代连续变量的微分方程。FDTD是将连续的空间划分为一个个的Yee元胞,以Yee元胞为空间电磁场离散单元,将麦克斯韦旋度方程转化为差分方程,结合计算机技术解决电磁学问题。
XFDTD6.3.8.4是Remcom公司开发的基于FDTD的电磁学仿真软件,可以应用于分析贵金属纳米颗粒的LSPR现象[12]。此软件可以很方便地进行可视化建模,有别于采用真实材料折射率的DDSCAT。XFDTD需要用Debye模型或者Lorentz模型来模拟金属在不同频率下的介电常数,从而带来误差。而且对于在连续光谱下的消光问题,需要将入射光源设置为高斯脉冲或者修正高斯脉冲来模拟一定波段光源的频谱,而结果通过傅里叶变换将时域的结果转化为频域的结果,优点是可以实时地仿真纳米颗粒与光作用的过程,很方便地输出纳米颗粒周围的电场分布图。
因此,本文将综合运用2种方法的优势,用DDSCAT分析各种纳米颗粒在不同波段的光谱,用XFDTD分析在具体光谱下的纳米颗粒表面的电场分布。在分析不同大小的纳米颗粒的消光现象的基础上,分析消光现象随2个纳米颗粒的间距以及入射光方向而产生的变化,以及纳米颗粒组成的阵列的消光现象。
2 纳米银颗粒的消光光谱以及周围的电场分布
利用DDSCAT软件,分析了大小为30 nm的硅球、二氧化硅球以及银球在可见光区域内的消光现象,它们分别代表纳米半导体、绝缘体和金属与入射光之间的相互作用。各折射率参数取自参考文献[13],仿真结果如图1所示。
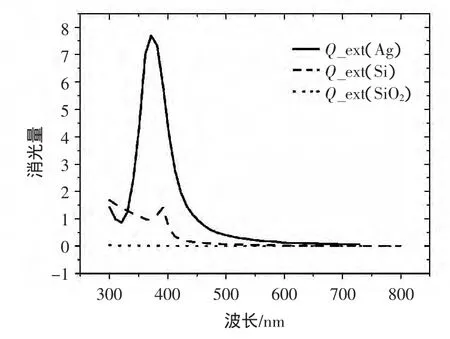
图1 不同材质的纳米颗粒的消光光谱
从图1中可以发现,二氧化硅的消光趋近于零,硅在波长391 nm处存在很弱的消光峰[14],银球在波长371 nm处产生很强的消光峰,此时发生了LSPR现象。
我们用XFDTD软件分析了半径为30 nm的银和二氧化硅2种颗粒周围的电场分布,银的Modified Debye模型参数取自文献[15],二氧化硅的折射率为1.47(介电常数为2.160,电导率为10-12S/m),入射光波长为371 nm(频率为8.42×1014Hz),沿x方向偏振,振幅为1 V/m,沿+z方向传播,得到在xy截面的表面电场分布。
从图2中可以看出,在x-y截面,银球表面的最大电场强度可达到23.99 V/m,而二氧化硅球的最大电场强度为1.546 V/m;银球的表面电场分布不均匀,有共振的现象发生,而二氧化硅球表面的电场分布变化不大。对比几种颗粒的消光光谱及表面的电场分布,可以看出只有金属才能明显地发生LSPR现象。这是由于金属的原子核带正电,而其周围的价电子带负电。在没有光照的作用下,可以把金属中的价电子看成是均匀正电荷背景中运动的电子气体,这种结构可以看作是一种等离子体,即金属表面等离子体。当特定波长的光入射到颗粒表面时,金属中的电子密度分布就会变得不均匀。设想在某一区域的电子密度低于平均密度,这样便形成局部的正电荷过剩。这时由于库伦引力的作用,会把邻近的电子吸引到该领域。而由于被吸引的电子具有惯性,又会使该区域聚集过多的负电荷。然后,电子间的排斥作用使电子再度离开该区域,从而形成价电子相对于正电荷背景的密度起伏振荡,这就是LSPR现象。

图2 不同材质纳米颗粒表面的电场分布
3 半径对球形银纳米颗粒消光的影响
郭伟杰等[16]通过Mie理论计算得到,银纳米颗粒的消光光谱随着颗粒半径R的大小而变化。当R<4 nm时,消光效率近似为0。当R在4~56 nm之间时,消光效率随波长变化的曲线是单峰的形式。而当56 nm 我们用DDA方法分析了半径R为5~50 nm的银纳米颗粒在光波长为300~800 nm的消光效率(Q_ext)、吸收效率(Q_abs)、散射效率(Q_sca)(Q_ext=Q_abs+Q_sca),仿真结果如图 3、4所示。 图3 不同大小的银纳米颗粒的消光效率、吸收效率、散射效率 图4 消光现象与银纳米颗粒半径之间的关系 从图3中可以看出,当R=5 nm时,Q_sca基本为0,Q_abs占Q_ext的主导地位,二者重合,消光峰在356 nm处;而当R=30 nm时,Q_abs和Q_sca差不多,消光峰在371 nm处,并且此时消光效率大于R=5 nm时的消光效率。记录不同大小的纳米颗粒的消光峰的位置,分析在光谱波峰时的Q_ext、Q_abs、Q_sca。消光峰位置与粒子半径R的拟合曲线为:消光峰波长(nm)λ=354.765 59-0.125 04R+0.026 3R2。 从图 4(b)可以看出,Q_ext、Q_abs 随着粒子半径R的增大先增大后减小。在R=40 nm时,Q_ext最大;R=24 nm时,Q_abs最大。Q_sca则一直随着颗粒半径的增大而增大。随着R增大,Q_abs/Q_ext越来越小,Q_sca/Q_ext越来越大[17],如图 4(c)所示。同样,用DDA方法分析了R为5~50 nm之间的银纳米颗粒分别在入射波长为200、400、600、800 nm时的Q_abs/Q_ext、Q_sca/Q_ext的变化规律。 图5 不同大小的银纳米颗粒在不同入射波长时的Q_abs/Q_ext、Q_sca/Q_ext 从图5中可以看出,不管是在消光峰处,还是在其他入射波长处,随着颗粒半径R的增大,Q_abs/Q_ext越来越小,Q_sca/Q_ext越来越大,即颗粒越大,散射效率所占的总消光效率的比例越大。 为了分析2个银纳米颗粒之间的耦合影响,取半径为 30 nm的 2个银球相隔距离 d=0、5、10、30、60 nm时的消光现象。当2个颗粒相互作用时,其消光现象及表面电场与入射光的方向有关,分别选取入射光平行于2个颗粒中心轴线和垂直于轴线的情况。 从图6中可以看出,当入射光方向平行于颗粒之间的连线时,随着颗粒间距的增加,消光峰位置产生红移。而当光线垂直于颗粒之间的连线时,随着颗粒间距的增加,消光峰位置产生蓝移。当2个颗粒距离为0 nm时,由于高阶偶极子的作用,产生多个消光峰。当2个颗粒的距离大于颗粒半径时,消光峰的位置与单个银颗粒的消光峰一致。 图6 消光光谱与纳米颗粒间距及入射光方向的关系 用XFDTD分析2个银颗粒耦合时周围电场的分布情况,取2个颗粒的轴线为z轴,当光线沿着z方向入射,沿y方向偏振时,则入射光方向与颗粒轴线平行;当光线沿着x方向入射,沿z方向偏振时,则入射光方向与颗粒轴线垂直。假设入射光电场方向的强度均为1 V/m,波长为371 nm(频率为8.42×1014Hz),则在2种入射光作用下,x-z截面上的电场分布分别如图 7(a)、(b)所示。 图7 d=10 nm时2个颗粒表面的电场分布 从图7中可以看出,当入射光方向平行于轴线时,最大电场强度为7.879 V/m,且集中于2个颗粒的两侧;而当入射光方向垂直于轴线时,最大电场强度为44.16 V/m,而且集中于2个颗粒之间。表面电场的大小也与2个纳米颗粒之间的距离有关。当d=0 nm时,表面最大电场强度可以达到129 V/m;当2个颗粒距离变大时,最大表面电场强度也减小。这是因为当光线平行于轴线时,其电场方向与入射光方向垂直,即电场方向垂直于2个颗粒连线方向,引起颗粒共振的方向与轴线垂直,此时2个颗粒之间的耦合作用较小。而当入射光垂直于轴线时,电场方向与颗粒轴线平行,引起共振的方向也与轴线平行,在2个颗粒之间由于偶极子的相互作用,产生很强的共振作用,导致其表面电场强度很大。纳米颗粒表面的等离子体是有一定距离的,所以相隔的越近,作用越剧烈。而当距离相对较大时,无论入射光的方向如何,2个颗粒的耦合作用都较小。 用DDSCAT分析R=30 nm的2个银纳米颗粒在相隔10 nm时,在不同介质(真空,n=1;水,n=1.33;丙酮,n=1.36;二氯甲烷,n=1.42;嘧啶,n=1.51)下的折射率灵敏度。2个纳米颗粒的消光峰波长折射率灵敏度为:当光垂直入射时,消光峰波长(nm)λ=244.757 59+171.878 6n;当光水平入射时,消光峰波长(nm)λ=252.168 6+131.200 7 n。即当光垂直入射时,2个纳米颗粒对于外界折射率的变化更敏感。 与纳米颗粒阵列相比,单个纳米颗粒在检测方面也有很多优点,如检测的极限更高,需要样品的容量更少,可以运用到多通道检测,不过制作费用较高[18]。因此,目前一般采用纳米球光刻(nanosphere lithography,NSL)技术在硅片或玻璃片上制作纳米颗粒的周期排列[19]。用DDSCAT分析方法,对半径为5 nm,任意2个球的间隔d分别为0及5 nm时的银纳米球的二维周期阵列在可见光范围内的消光光谱进行了分析,其结果如图8所示。 图8 不同间距的银纳米球周期阵列的消光光谱 从图8中可以看出,周期排列的银纳米球阵列出现2个消光峰,d=0 nm的2个消光峰分别在372.92和643.75 nm处,在372.92 nm处的消光峰主要是由吸收引起的,643.75 nm处的消光峰比第一个峰的强度大很多,主要是由散射引起的。这是由于当纳米颗粒之间的距离为0时,纳米颗粒的总体形状变得复杂,出现多偶极子的共振,因而出现第二个消光峰。而d=5 nm时的第二个消光峰明显比第一个消光峰弱,可以预测当周期阵列型的纳米颗粒间距相对较大时,其消光峰会与单个纳米颗粒的消光峰一致,即为单峰形式。 为了分析银纳米球及其阵列的折射率灵敏度,假设待测介质环境分别为真空(n=1)、水(n=1.33)、丙酮(n=1.36)、二氯甲烷(n=1.42)及嘧啶(n=1.51)等,分析比较它们的消光现象,如图9所示。 由图9(b)可知,2个消光峰的位置波长与外部介质的折射率拟合直线为:消光峰1波长(nm)λ=214.9+157.0n;消光峰 2波长(nm)λ=116.1+527.7n。消光峰1的折射率灵敏度为157.0 nm/RIU,消光峰2的折射率灵敏度为527.7 nm/RIU。而单个5 nm银球的消光峰波长(nm)λ=223.4+132.5n。第一个消光峰的折射率灵敏度与单个银纳米颗粒相近,而第二个消光峰由于纳米颗粒之间的耦合作用其灵敏度增大。 图9 银纳米球阵列在不同外部介质下的消光光谱和折射率灵敏度 金属纳米颗粒的LSPR消光现象与纳米颗粒的种类、大小、形状及所处的介质环境有关。本文重点分析了贵金属纳米颗粒LSPR现象与颗粒大小以及颗粒之间的耦合作用的影响,对比分析了金属球与绝缘体球及半导体球的消光光谱以及表面电场分布,验证了LSPR现象产生的原因。通过对不同大小的纳米颗粒的消光、吸收、散射光谱的分析得知,当纳米颗粒半径较小时,消光峰位置波长随颗粒半径变化不大,随着颗粒半径的增大,散射效率占总的消光效率的比重增加。并分析了2个纳米颗粒的耦合作用,发现当入射光方向垂直于轴线,且纳米颗粒之间间距较小时,耦合的作用较大。同样纳米颗粒阵列的消光光谱的灵敏度与纳米颗粒的大小以及间距有关,当颗粒间距很小的时候会出现多峰形式的消光谱。 [1] David Thompson.Michael Faraday′s recognition of ruby gold:The birth of modern nanotechnology references[J].Gold Bulletin,2007,40(4):267-269. [2] Prashant K J,Ivan H E.An nanoparticles target cancer[J].Nanotoday,2002,2:19-29. [3] JeffreyM McMahon.Gold nanoparticle dimer plasmonics:Finiteelement method calculations of the electromagnetic enhancement to surface-enhanced Raman spectroscopy[J].Anal Bioanal Chem,2009,394:1 819-1 825. [4] Moharam MG,Gaylord TK.Rigorous coupled-wave analysis of planar-grating diffraction[J].OptSoc Am,1981,71(7):811-818. [5] Draine B T.The discrete-dipole approximation andIts application to interstellar graphite grains[J].The Astrophysical Journal,1988,333(22):848-872. [6] Yao HM,Li Z,Gong QH.Coupling-induced excitation ofa forbidden surface plasmon mode of a gold nanorod[J].SciChina Ser G Phys Mech Astron,2009,52(8):1 129-1 138. [7] Zhou Fei,Li Zhi-Yuan.Quantitative analysis of dipole and quadrupole excitation in the surface plasmon resonance of metal nanoparticles[J].JPhys Chem C,2008,112:20 233-20 240. [8] Devoe H.Optical properties of molecular aggregates.I.Classical model of electronic absorption and refraction[J].JChem Phys,1964,41:393-400. [9] YangW H,SchatzGC.Discrete dipole approximation for calculating extinction and Raman intensities for small particles with arbitrary shapes[J].JChem Phys,1995,103:869-875. [10] Kelly K L,Lazarides A A,Schatz G C.Computational electro maganetics of metal nanoparticles and their aggregates[J].Nnao technology,2001,12:67-73. [11] Kane Yee.Numericalsolution of initial boundary value problems involving Maxwell′s equations in isotropic media[J].IEEE Transactionson Antennas and Propagation,1966,14:302-307. [12] Zhang Hai-xi,Gu Ying,Gong Qi-huang.A visible-near infrared tunable waveguide based on plasmonic gold nanoshell[J].Chinese Phys B,2008,17(7):2 567-2 573. [13] Edward DPalik.Handbook of optical constants of solids[M].Washington DC:Academic press,1985:286-297,350-359. [14] Wilcoxon JP,Samara G A.Tailorable,visible light emission from silicon nanocrystals[J].Applied Physics Letters,1999,74(21):3 164-3 166. [15] GaiHongfeng.Modified Debye model parameters of metals applicable for broadband calculations[J].Applied Optics,2007,46(12):2 229-2 233. [16] 郭伟杰,张媛,李强,等.银纳米颗粒半径对其消光光谱影响的研究[J].新疆大学学报:自然科学版,2008,25(2):187-189. [17] Eun ChulCho,Chulhong Kim, FeiZhou,etal.Measuring the optical absorption cross sections of Au Ag nanocages and Au nanorods by photoacoustic imaging[J].J Phys Chem C, 2009,113(21):9 023-9 028. [18] Stuart D A.Biological applications of localised surface plasmonic phenomenae[J].IEEProc Nanobiotechnol,2005,152(1):13-32. [19] Christy L Haynes, Richard PVan Dugne.Nanosphere lithography:A versatile nanofabrication tool for studies of size-dependent nanoparticle optics[J].J Phys Chem B,2001,105:5 599-5 611.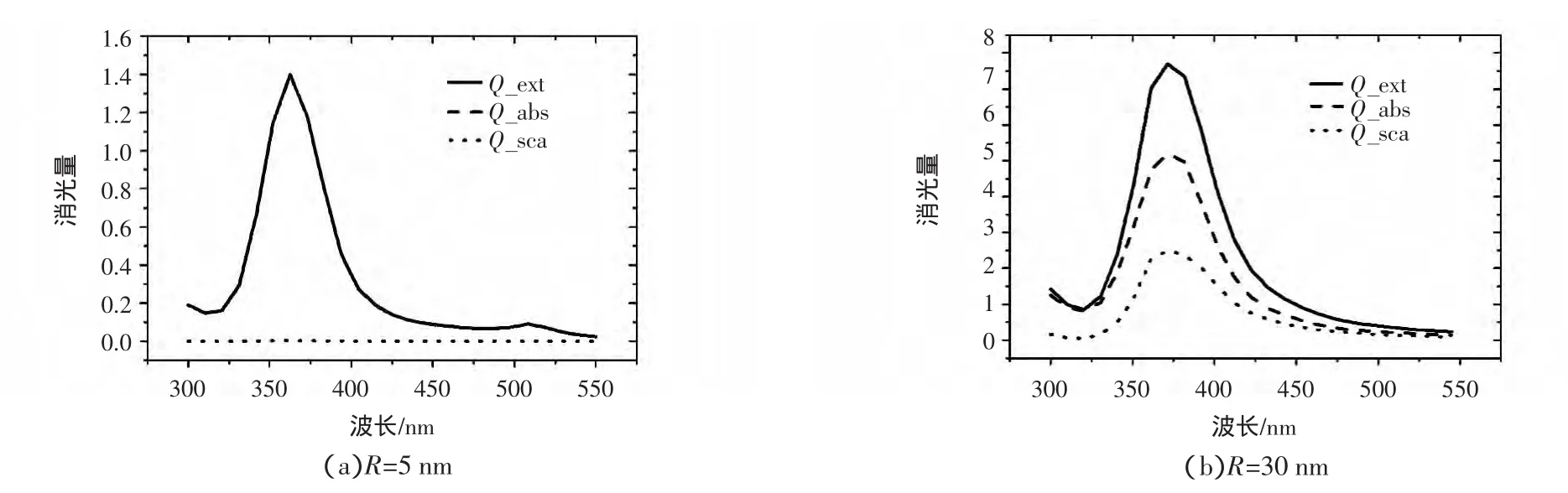

4 纳米颗粒之间的耦合作用


5 银纳米球及其阵列的消光光谱与折射率灵敏度分析


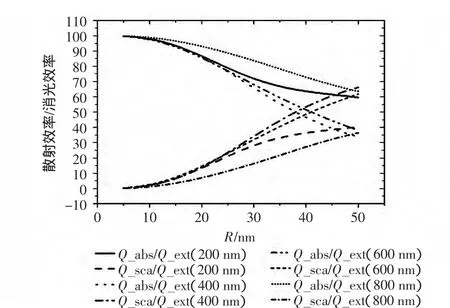
6 结论
