基于Fuch映射的混沌蝙蝠算法
2014-11-22孙文捷张惠珍
孙文捷, 张惠珍, 张 健, 赵 坤
(上海理工大学 管理学院,上海 200093)
近十几年内炙手可热的遗传算法、神经网络、模拟退火算法、蚁群算法、微粒群算法等[1],都是受自然规律和生物群体智能行为的启发而提出,其在广泛的科学和工程技术领域内显示了其独特的能力和应用效果.但是,这类算法在求解复杂问题时,也暴露出其固有的一些缺陷,如算法易陷入局部极值,求解精度不高,而且许多算法的理论基础较薄弱,没有形成统一的算法框架,仍有许多问题有待研究.受蝙蝠回声定位行为的启发,Yang[2]于2010年提出一种新型的元启 发 式 算 法——蝙 蝠 算 法(bat-inspired algorithm BA).已有研究表明,BA 在某些方面将粒子群算法、遗传算法和和声算法的主要优点进行了良好的结合,并且粒子群算法和和声算法可以认为是蝙蝠算法在经过适当简化后的一种特殊情况.因此,BA 较其它算法具有发挥更大作用的潜能[2-3].混沌是一种普遍的非线性现象,具有遍历性、随机性与确定性相统一、对初始值变化敏感等特点[4].由于遍历性可使搜索过程避免陷入局部极小,因此,混沌搜索已成为一种非常有效的优化算法.针对传统混沌优化方法中优化结果对搜索初始值要求极高以及搜索效率较低的问题,傅文渊等[5]提出一种自适应折叠混沌优化方法——Fuch映 射,与Logistic映 射[6]、Chebyshev映 射[7]和Tent映射[8]相比,Fuch映射具有更强的混沌特性.针对基本蝙蝠算法搜索效率低和较易陷入局部最优的缺点,本文在基本蝙蝠算法中引入了Fuch映射,设计了一种基于Fuch映射的蝙蝠算法——Fuch混沌蝙蝠算法(FCBA).算法循环过程中:一方面,通过混沌遍历频率变化区间,使得蝙蝠的速度能得到充分变化;另一方面,在蝙蝠所发射的脉冲速率还不太高时,利用Fuch映射对局部最优解的邻域进行混沌遍历搜索,使其跳出局部最优解.通过求解基准测试函数对FCBA与BA 的寻优能力和搜索效率进行比较.结果表明,与基本蝙蝠算法相比,FCBA 具有全局搜索能力强和收敛速度快的优点.
1 蝙蝠算法
1.1 蝙蝠的回声定位能力
蝙蝠是一种神奇的动物,有高级的回声定位能力.微型蝙蝠靠一种声纳,也称为回声定位器,来探测猎物,避免障碍物,在黑暗中找到它们的栖息地.这些蝙蝠发出响亮的声音脉冲,然后聆听从周围的物体反弹回来的回声,利用双耳的时间差及回声的响度变化去建立周围环境的三维场景.
大多数蝙蝠用短波、调频信号对一个音阶横扫,而另一些蝙蝠则更经常使用固定频率的定位信号.它们的信号带宽变化取决于物种,并经常通过使用更多谐波来提高,但是它们探测猎物和避免障碍的原理都是基于回声定位的声学原理.研究显示:蝙蝠发出的脉冲频率通常为25~150kHz.由声音在空气中的速度v=340m/s及超声波在频率f 下的波长λ=v/f 可知:蝙蝠发出的脉冲波长λ在2~14mm之间,这样的波长类同于它的猎物的大小.此外,蝙蝠发出在超声波范围内的声波,其响度能达到110dB,且响度可以从搜索猎物时的最高变化到靠近猎物时的最小.
1.2 蝙蝠运动的数学描述
1.2.1 蝙蝠的速度更新和位置更新
假设搜索空间为D 维,第i只蝙蝠在第t次进化时的位置和速度分别为和,则在第t+1次进化时,其位置和速度可分别更新为和,即
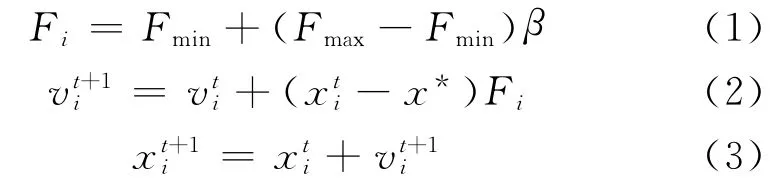
式中,Fi,Fmax和Fmin为第i只蝙蝠在当前时刻发出的声波的频率、声波频率的最大值和最小值;β为随机数,β∈[0,1];x*为当前最优解.
对于大小为n 的蝙蝠群体,可以从中选择一只蝙蝠(解),并更新该蝙蝠相应的位置,即在被选择解的附近产生一个新解
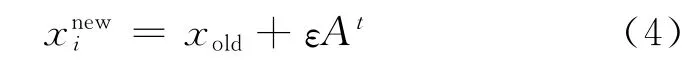
该过程可被理解为局部搜索过程.其中,xold为从当前最优解集中随机选择的一个解,At为当前代前i只蝙蝠的平均响度;ε为随机向量ε∈[-1,1]D.
1.2.2 响度和脉冲发射
蝙蝠实际捕猎过程中,其声波响度A(i)随着与猎物距离的减小而不断减弱,但脉冲发射速率R(i)随着与猎物距离的减小而逐渐提高.蝙蝠i脉冲的响度A(i)和发射速率R(i)可更新为
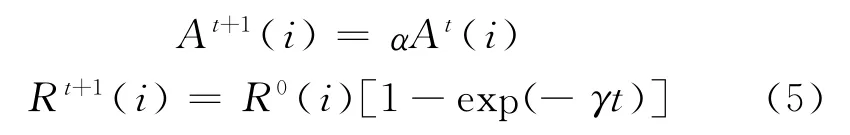
其中,0<α<1和λ>0均为常量.A(i)=0时意味着蝙蝠i刚刚发现一只猎物,暂时停止发出任何声音.不难发现t→∞,At(i)→0,Rt(i)=R0(i).
上述现象反映在实际算法中,即随着响度的不断减弱和脉冲速率的不断提高,蝙蝠以一定的概率进行局部搜索和接受新解;但是,进行局部搜索的概率随着脉冲速率的不断提高而降低,接受新解的概率随着响度的不断减弱而降低.这既反映了蝙蝠的实际捕猎情况,也有助于加快算法收敛,并在算法运行初期能够跳离局部最优.
基本蝙蝠算法中,蝙蝠的速度和位置的更新策略和标准粒子群算法更新速度和位置的策略有些相似之处.虽然从某种程度上来讲,蝙蝠算法可视为标准粒子群优化和由响度和脉冲速率控制的集中局部搜索的一种均衡组合.但是,与其它仿生类智能优化相似,基本蝙蝠算法仍有容易陷入局部最优的不足之处.
2 Fuch映射
Fuch映射是一种新型的一维离散映射,其表达式为
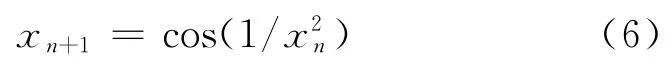
其中,xn≠0,n∈Z+.文献[5]对Fuch映射的不动点特性和Lyapunov指数[9]进行了深入研究,并计算得到Fuch映射的Lyapunov指数λ 为2.165.与传统的混沌映射(如Logistic映射、Chebyshev映射和Tent映射)相比,Fuch映射有如下优势[5]:
a.Fuch映射具有更强的混沌特性,给定微小的初始值变化,混沌映射产生的输出是完全不同的,并且系统输出毫无规律;
b.映射相比于Logistic映射和Tent映射在解空间内具有更加均衡的遍历性;
c.考察遍历整个系统解空间的混沌迭代次数时,Fuch映射与传统有限折叠混沌映射相比具有更小的迭代次数,能更好地实现混沌寻优;
d.Fuch映射的不动点为超越数,若初始值不为0,则该映射产生的混沌不收敛于有理数不动点,表明在初始值不为0的情形下均能产生混沌.
Fuch映射有不因初值设置不当而陷入不动点(局部最优)的优点.因此,将Fuch映射引入基本蝙蝠算法,其可以不依赖蝙蝠初始搜索的精度,对局部最优解的邻域进行混沌遍历搜索.
3 基于Fuch映射的蝙蝠算法
3.1 频率变化区间的混沌搜索
在基本的蝙蝠算法中,每只蝙蝠利用特有的回声定位能力,测算出自己与当前所求得的最优解间的距离,并根据自动发出的脉冲频率来调节自己的速度.但是脉冲频率往往是从[Fmin,Fmax]中随机取得,这很有可能使速度的变化落在某个局部的区间中,根据式(3)可知:特别是在蝙蝠很靠近所搜索到的当前最优解时,速度会被迫“停滞”,这就影响了蝙蝠的搜索效率.另一方面,在蝙蝠的脉冲发射速率不断升高后,进行邻域搜索的机会将越来越小,这使得蝙蝠对所搜索到的初始解的依赖性加大,这很有可能使算法陷入局部最优.
为了改进基本蝙蝠算法的上述不足之处,本文定义第i只蝙蝠在第t 次进化时产生混沌变量,并利用其对频率变化区间进行混沌搜索
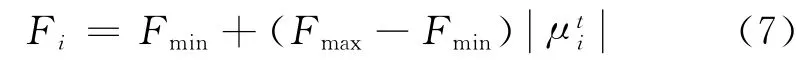
与式(1)相比,式(7)使得蝙蝠在靠近当前最优解的同时,其速度依然能得到充分变化.
3.2 局部最优解邻域的混沌搜索
基本蝙蝠算法中的局部搜索为:从现有的最佳解决方案中选择一只蝙蝠后,每只蝙蝠的新位置在随机游走中就近产生.为了进一步改善基本蝙蝠算法的局部搜索功能,改善其容易陷入局部最优的不足之处,使其能够较快地求出所求问题的最优解或满意解,本文利用Fuch映射对基本蝙蝠算法的局部最优解邻域进行混沌搜索,具体搜索步骤如下:
Step1 产生随机数rand,若rand>Ri,则进行局部搜索,否则不进行局部搜索;fnew 为蝙蝠初始位置所相应的目标函数值;
Step 2 确定以当前最优解x*为中心的邻域搜索半径
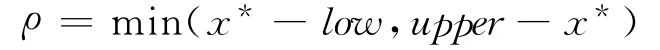
式中,low 和upper 分别为变量的上下界.
Step 3 令第t次进化中第i 只蝙蝠所产生的混沌变量为本次邻域搜索的初始混沌变量k0;记总迭代次数为m,临时变量为temp,为第i 只蝙蝠第t次进化时所搜索到的新解.以最小化问题为例,混沌遍历搜索过程为
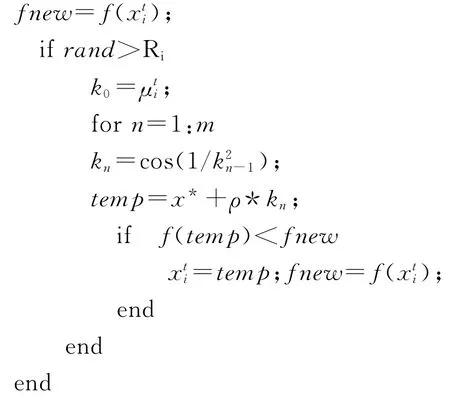
3.3 Fuch混沌蝙蝠算法
为了使基本蝙蝠算法能够跳出局部最优,通过较小地迭代次数搜索到全局最优解,本文不仅利用Fuch映射对频率变化区间和局部最优解邻域进行混沌搜索,而且在每次进化迭代开始前对Fuch 映射的初值进行赋值扰动,得到一种新型蝙蝠算法——Fuch混沌蝙蝠算法,简记为FCBA.
假设求函数f(x)的最小值,算法最大循环次数为gen,蝙蝠种群大小为n,第i只蝙蝠的位置为xi,速度为vi,脉冲发射速率为Ri,脉冲响度为Ai,个体适应值fitness(i)=f(xi).用于求解f(x)的FCBA算法的基本步骤可以概括如下:

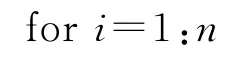
对蝙蝠的频率变化区间进行混沌搜索,更新其速度和位置,并对蝙蝠的速度与位置进行越界处理;
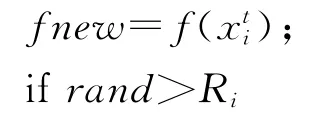
对局部最优解的邻域进行混沌遍历搜索


更新当前最佳解x*及其对应的速率、脉冲发射速率、脉冲响度和脉冲频率;
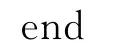
增大Ri,减小Ai;
邻域搜索半径ρ的确定方法已经可以避免位置越界的发生,因此上述FCBA 算法中只对蝙蝠的初始搜索进行位置纠偏.
4 仿真实验
为测试算法的求解性能,本文利用基本蝙蝠算法和FCBA 算法对4个经典函数优化问题进行求解.为了确保两种算法具有可比性,使它们在相同的起点上进行比较,计算过程中,不仅对两种算法共有的绝大部分参数设定了相同的值(如表1所示),而且对两种算法设置了相同的迭代次数,但对其求解精度没有设置.

表1 参数设置Tab.1 Setting up of parameters value
表2给出了4个测试函数及其变量取值区间和全局最优解.除函数f4(x)为单模函数,无局部最优解,只有全局最优解外,其它3个函数都是典型的多峰函数,有多个极小值,均较难优化,常用来测试算法的全局寻优能力.

表2 4个标准测试函数Tab.2 4Benchmarkfunctions
算法运行环境为Windows 764 位操作系统,Intel处理器,2.40 GHZ,4 GB内存;仿真软件为MatlabR2012a.
表3和表4(见下页)分别给出了4个测试函数利用基本蝙蝠算法和FCBA 算法的求解结果.
对比表3和表4中的数据,不难发现:FCBA 与BA 求解4个测试函数时,所耗费的计算时间相差并不很大,但FCBA 在寻优精度上却有着较大优势,尤其求解f2(x),f3(x)和f4(x)时,FCBA 在寻优精度上的优势特别明显,其求解结果在最好值、最劣值和平均值3方面均明显优于基本蝙蝠算法的计算结果.
给定相同的迭代次数,两种算法所耗费的计算时间相差并不大.为了进一步分析算法的收敛性能,图1(见下页)给出了两种算法求解4个测试函数的迭代收敛曲线,图1中(a),(b),(c)和(d)的横坐标表示进化迭代次数gen,纵坐标表示函数值f(x).
从图1可知,与BA 相比,FCBA 能够较快地收敛于全局最优解,其在较小的进化迭代次数内便可接近所测函数的理论全局最优解.

表3 FCBA 的算法寻优结果Tab.3 Results obtained byu singFCBA

表4 BA 的算法寻优结果Tab.4 Results obtained by using BA

图1 目标函数随循环次数的变化曲线Fig.1 Changing curve of the objective function value
5 结 论
将Fuch映射引入到基本蝙蝠算法中,设计了一种混沌蝙蝠算法.算法中,一方面,在蝙蝠的脉冲发射速率还不是很高,即蝙蝠还没有很靠近猎物时,对局部最优解的邻域进行混沌遍历搜索,大大优化了初始值的质量与逼近全局最优解的速度;另一方面,通过对局部最优解的邻域进行混沌遍历搜索,不仅有效地改善了蝙蝠初始搜索所得到的解,而且对基本蝙蝠算法的局部搜索功能进行了很好的改进,使其在较小的进化迭代次数内较快地收敛于全局最优解或求得问题的满意解.仿真结果表明:提出的混沌蝙蝠算法求解函数优化问题时,在收敛速度和精度上均优于基本蝙蝠算法,且具有一定的可行性和较好的寻优能力.
[1]王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001.
[2]Yang X S.A new metaheuristic bat-inspired algorithm[J].Nature Inspired Cooperative Strategies for Optimization,2010,284:65-74.
[3]Yang X S,Gandomi A H.Bat algorithm:a novel approach for global engineering optimization[J].Engineering Computation,2012,29(5):267-289.
[4]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.
[5]傅文渊,凌朝东.自适应折叠混沌优化方法[J].西安交通大学学报,2013,47(2):33-38.
[6]范九伦.分段Logistic混沌映射及其性能分析[J].电子学报,2009,37(4):720-725.
[7]石军.基于Chebyshev映射的混沌特性及其性能分析[J].现代电子技术,2008(23):93-96.
[8]单梁,强浩,李军,等.基于Tent映射的混沌优化算法[J].控制与决策,2005,20(2):179-182.
[9]李小亭,蔡诗东.混沌和李亚普诺夫特征指数[J].物理,1996,25(5):282-285.
