奇数阶幻方的构造与特征值分析

刘乐乐

（上海理工大学 理学院，上海 200093）

1 问题的提出

关于幻方的研究由来已久，中国古书《易经》中记载的洛书是世界上最早的幻方.随后，幻方传入世界各地，引起了广泛关注，取得了许多成果.幻方不仅具备美感，还蕴含着许多奇特的奥秘，具体可参看文献［1－3］.随着计算机的快速发展，幻方广泛应用于人工智能、图像处理、图论及对策论等方面.

定义1 对任意的正整数n≥3，将1，2，…，n2填入n×n的矩阵中，使得矩阵的每行、每列及对角线之和均为同一个数s，这样的矩阵称为幻方矩阵（或魔方矩阵），简称为幻方，s为幻方值.

显然，n阶幻方中所有整数的和为

按照幻方的定义即知2s＝n（n2＋1）.

文献［4］通过对幻方矩阵特征值的分析，给出了一种构造奇数阶非奇异幻方的方法，但并未给出其特征值的计算公式.文献［5］给出了幻方的精彩应用案例.文献［6］讨论了奇数阶幻方的一种构造方法.除此之外，幻方的构造方法还有很多，在文献［2］中有详细的介绍.文献［7］给出了利用线性空间理论来构造幻方的方法.文献［8］对奇数阶幻方特征值给出了一个猜测：奇数阶幻方的特征值均为实特征值，除最大特征值为幻方矩阵的幻方值外，其它特征值正负成对出现.

现对文献［7］中奇数阶幻方的一种构造方法进行改造，给出奇数阶幻方的一种代数表示方法.基于这种表示法，应用循环矩阵和对称循环矩阵的性质，对奇数阶幻方特征值进行分析，最后给出奇数阶幻方全部特征值的统一计算公式.因此，发现文献［8］中关于奇数阶幻方特征值的猜想是错误的.

为了分析奇数阶幻方特征值的性质，需要以下的概念与结论.

定义2［9］若n阶复矩阵A∈ℂn×n具有形状

则称A 为n 阶循环矩阵，记为A＝circ（a0，a1，…，an－1）.称π＝circ（0，1，0，…，0）为 基 本 循 环 矩阵，即

显然，π为正交矩阵，则必为正规矩阵，从而π在复数域上可以对角化.因为，πn＝E 且πk≠E（其中，k＜n为 正 整 数，E 为 单 位 矩 阵），所 以，π 的n个特征值分别为1，ε，ε2，…，εn－1，其中，ε为n次单位原根，相对应的特征向量为α0，α1，…，αn－1，可解得

定义3［9］若n阶复矩阵B∈ℂn×n具有形状

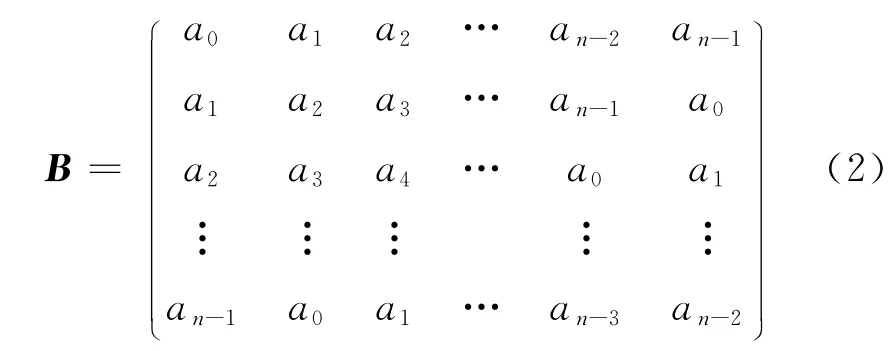
则称B 为n 阶对称循环矩阵，记为B＝sc（a0，a1，…，an－1）.称σ＝sc（0，0，…，0，1，0）为基本对称循环矩阵，即

引理1［9］矩阵A，B 由式（1）和（2）定义，则有表示

2 奇数阶n＝2m＋1（m≥1）幻方的构造

引理2中关于奇数阶幻方的构造方法引自文献［7］.

引理2 矩阵M＝n An＋Bn＋Hn为n＝2 m＋1（m≥1）阶幻方，其中

即

Bn为An逆时针旋转90°所得矩阵，Hn为元素全为1的矩阵.

现对这种构造作以下改造.为此，先证明引理3.

引理3 矩阵π 为基本循环矩阵，σ 为基本对称循环矩阵，则有

证明 易验证σπn－1＝σπnπ－1＝σπ－1，从而有πσ＝σπn－1成立.往证另一算式成立.由πσ＝σπn－1可得

结合引理2和引理3可得定理1.

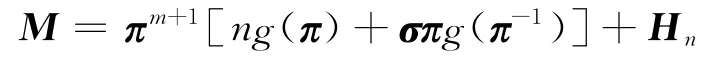
证明 由引理1和引理2可将M 写成

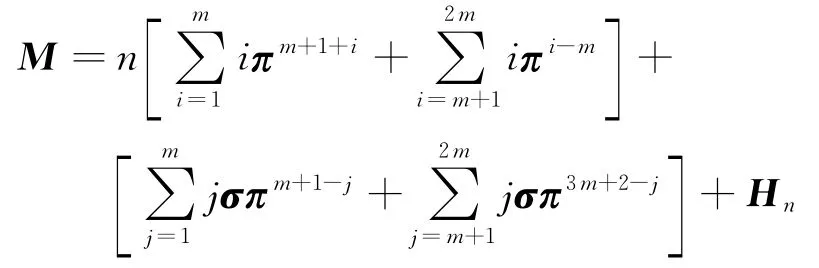
结合引理3及恒等式πn＝π2m＋1＝E，得

3 幻方特征值的计算

现基于定理1求出奇数阶幻方的特征值.由于相似矩阵具有相同的特征值，因此，要计算幻方矩阵M 的特征值，只需考虑矩阵P－1MP.结合文献［10］可得定理2.

定理2 存在n 阶可逆矩阵P，使得P－1πP 和P－1HnP 均为对角阵，且

证明 令P＝（α0，α1，…，αn－1），其中，αi＝（1，εi，ε2i，…，ε（n－1）i），i＝0，1，…，n－1.显然，P 是范德蒙矩阵，从而P 可逆.易验证P－1πP＝diag（1，ε，ε2，…，εn－1），P－1HnP＝diag（n，0，0，…，0）.由引理3，πσ＝σπ－1，有

记P－1σP＝（aij）n×n，即为

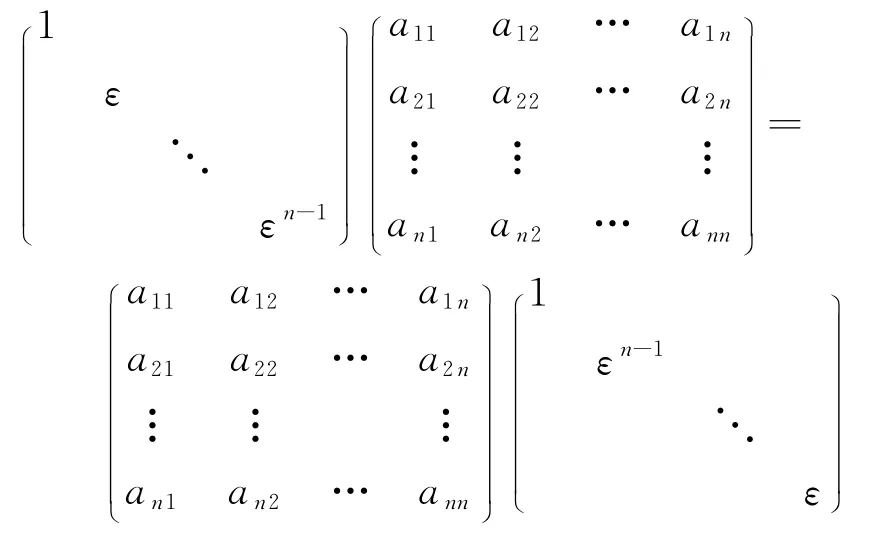
解得

进一步，将P＝（α0，α1，…，αn－1）代入式（3），得uk＝ε2k，k＝0，1，2，…，n－1.

由定理1计算得

因此，结合定理2，有定理3.

定理3 令f（x）＝xm＋1g（x），则

定理4 对任意正整数k，0≤k≤n，有

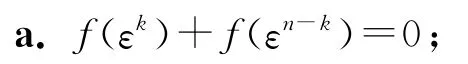
证明 利用Abel分部求和公式［11］，得

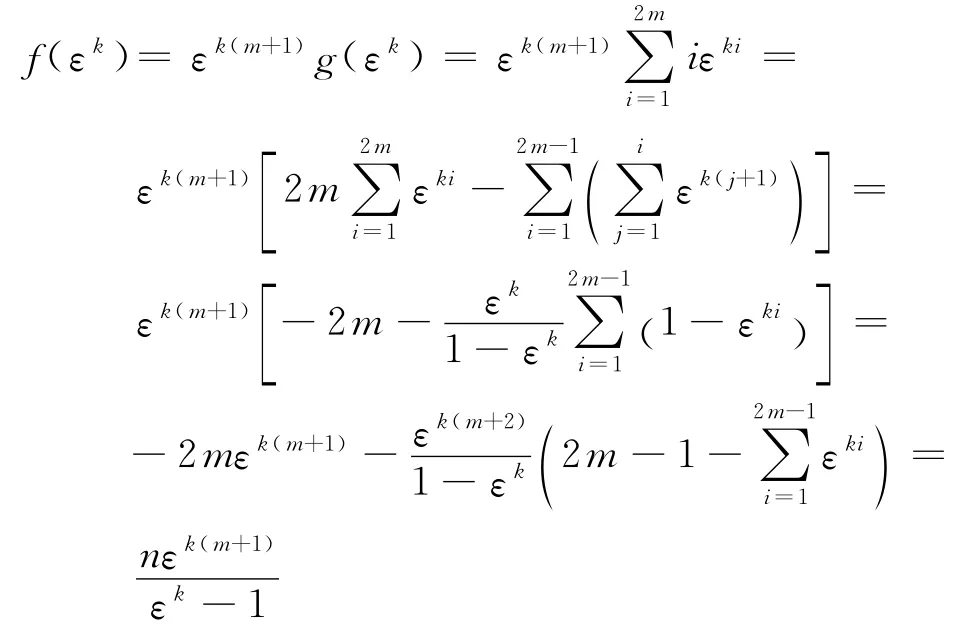
现证明a和b成立.

即定理4成立.

由定理2～4得定理5.定理5给出了奇数阶幻方全部特征值的统一计算公式.

定理5 n＝2m＋1（m≥1）阶幻方M 的全部特征值为

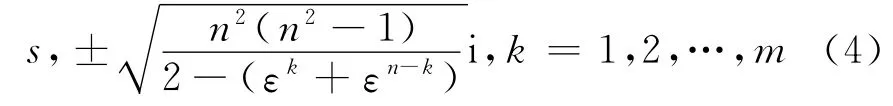
式中，i为虚数单位，即i2＝－1.

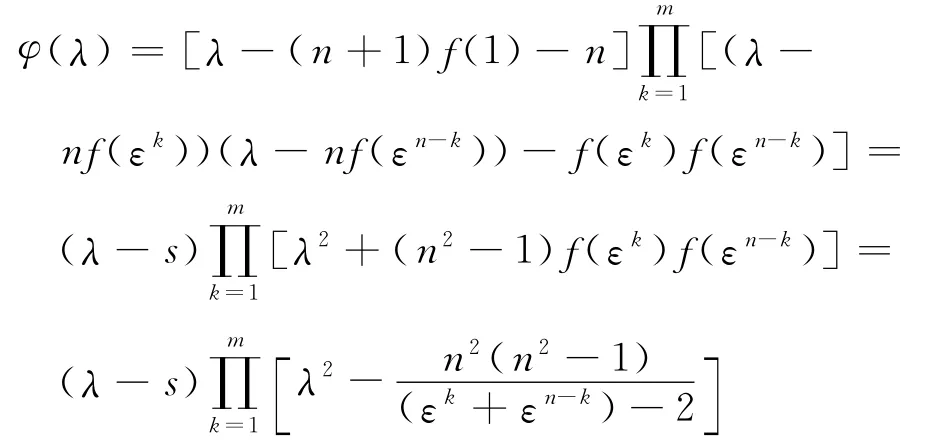
对任意正整数k，εk与εn－k总是共轭的，因此，εk＋εn－k∈ℝ，且有

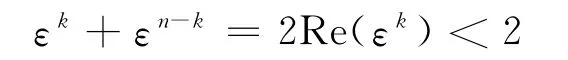
于是，令φ（λ）＝0，可知M 的全部特征值由式（4）给出.

4 结 论

研究结果表明，奇数阶幻方矩阵有实特征值s，其它特征值均为纯虚数且共轭出现，其数值由式（4）给出.鉴于此，发现文献［8］中关于奇数阶幻方的特征值的猜想是错误的.例如，当n＝3时，3阶幻方的特征值分别为其特征值中有纯虚数，并非全是实数.

［1］汪潘义，代诗平.神奇的奇数阶幻方［J］.合肥学院学报，2007，17（4）：20－23.

［2］吴鹤龄.幻方及其他——娱乐数学经典名题［M］.北京：科学出版社，2004.

［3］Pickover C A.The zen of magic squares，circles，and stars［M］.Princeton：Princeton University Press，2002.

［4］Lee M Z，Love E，Narayan S K，et al.On nonsingular regular magic squares of odd order［J］.Linear Algebra and its Applications，2012，437（6）：1346－1355.

［5］Aronov B，Asano T，Kikuchi Y，et al.A generalization of magic squares with applications to digital halftoning［J］.Theory Comput Syst，2008，42（2）：143－156.

［6］廖云儿，祝宝满，吴连发.求解奇数阶幻方的一个简单方法［J］.数 学 的 实 践 与 认 识，2007，37（24）：174－177.

［7］李尚志.线性代数精彩应用案例（之一）［J］.大学数学，2006，22（3）：1－8.

［8］单润红，高峰，宋君强.魔方矩阵的特征值分析［J］.高等数学研究，2004，7（4）：45.

［9］江兆林，周章鑫.循环矩阵［M］.成都：成都科技大学出版社，1999.

［10］袁晖坪.行（列）对称矩阵的满秩分解和正交对角分解［J］.上海理工大学学报，2007，29（3）：260－264.

［11］陈纪修，於崇华，金路.数学分析（下册）［M］.2版.北京：高等教育出版社，2004.