回收再制造企业生产计划与需求协调研究

邓爱民，蒋福展

（湖南大学 工商管理学院，湖南 长沙 410082）

一、引 言

自然资源数量的有限性以及过度开采资源而导致资源濒临枯竭，促使越来越多的企业积极投身于产品回收，通过回收再制造生产的产品接近或者达到新产品的性能，一方面有效利用资源，另一方面降低企业生产成本。

近年来，国内关于回收再制造的研究主要集中在两个方面：一是回收模式；二是回收定价。对于回收模式研究，姚卫新[1]通过建立数学模型与实例验证为企业选择合适的回收模式提供了初步的理论依据；赵忠和孔令丞提出了再制造生产计划管理具有科学性与适用性分析的方法手段[2～3]；李帮义[4]建立了需求不确定下三种不同回收模式下的再制造闭环供应链模型，并给出求解优化条件以及利用数值仿真对其求解和比较分析。对于回收定价研究，李响[5]建立了企业回收价格的优化模型，并证明了在考虑企业风险不同态度下最优回收价格是唯一的；彭志强[6]构建了基于再制造和顾客等待的差别定价模型；王文宾、孙浩和包晓英分别从市场细分、产品差异和回收再制造角度对闭环供应链的定价问题进行了研究[7～9]。国外关于回收再制造的文献主要集中在生产批量和提前期这两个方面。对于生产批量研究，Naeem和Dias[10]假设需求量和回收量是随机确定的，研究了生产和再制造过程中单个项目动态生产批量问题；Pan和Tang[11]提出一个伪多项式算法去解决回收再制造闭环供应链的动态生产批量问题。对于提前期研究，Kiesmuller[12]研究了不同生产和再制造提前期下随机回收系统的控制问题；Inderfurth和van der Laan[13]通过改变再制造提前期来影响系统总成本，得到一个最佳再制造提前期以使系统达到最优状态；Poles[14]使用系统动力学方法构建了回收再制造的生产和库存模型，分析了生产提前期和再制造提前期的变化对企业总成本的影响。

国内外关于回收再制造生产计划方面的文献则相对较少，景熠[15]建立了库存和生产能力受限的混合整数规划模型，并引入双倍体遗传算法对仿真算例进行求解；李勇建[16]建立了多类短生命周期产品的系统动力学模型，并分析需求率和回收率等参数的变动对生产计划安排及总利润的影响。Shi和Zhang[17]研究了在一个总产能受到约束的情况下，多产品闭环供应链系统中的制造商如何确定新产品和再制造产品的生产数量以及二手产品的收购价格以达到期望利润的最大化。本文的思路与Shi和Zhang[17]类似，同时借鉴Poles[14]构建回收再制造设施的方法并运用系统动力学相关理论建立了回收再制造企业的单产品闭环回收再制造模型，研究了回收产品的生产计划与需求相协调问题，并分析了回收再制造企业的再制造能力的变化对企业利润和缺货率的影响。

二、问题描述

本文考虑在不同需求条件下生产单一产品的回收再制造企业生产计划安排问题，即在高需求和低需求这两种不同需求情况下企业的回收产品再制造能力和新产品生产能力如何分配的问题。回收再制造企业生产的这种产品具有短生命周期的特性，同时本文与Georgiadis、Vlachos以及Shi和Zhang等学者一样，都假设再制造产品和新产品没有任何区别且消费者对两者没有消费偏好，它们可以以同样的价格在同一个市场上进行销售[18～20]。本文在这里做了如下假设：

（1）制造商是利润驱动型企业，希望获得利润最大化同时又保持较高的顾客满意度。

制造商会通过调整回收再制造生产计划来保证利润的最大化，这主要是通过调整回收产品的再制造能力和新产品的生产能力之间的比例分配来实现的，而企业总的产品生产能力在模型仿真期间保持不变。

（2）回收产品再制造成本远小于新产品生产成本，因此制造商在回收再制造生产计划决策时会优先选择再制造，再制造能力不能够满足需求时再选择新产品的生产。

三、因果图模型

基于系统动力学工具，可以给出研究问题的因果回路图，如图1所示。

本文把回收的产品称为回收件，质量检验合格的回收件称为可用回收件，可用回收件被再制造后称为再制造产品，与新生产的产品同时进入成品库存以供应市场的需求。再制造能力比例是企业回收产品的再制造能力占企业产品生产总能力的百分比，生产能力比例是企业新产品的生产能力占总能力的百分比。

在图1中包含5个状态变量（市场上此产品的总量、回收件库存、可用回收件库存、成品库存、累积订单），通过状态变量就可以将时间对订单、回收件和产品等的累积作用储存起来。

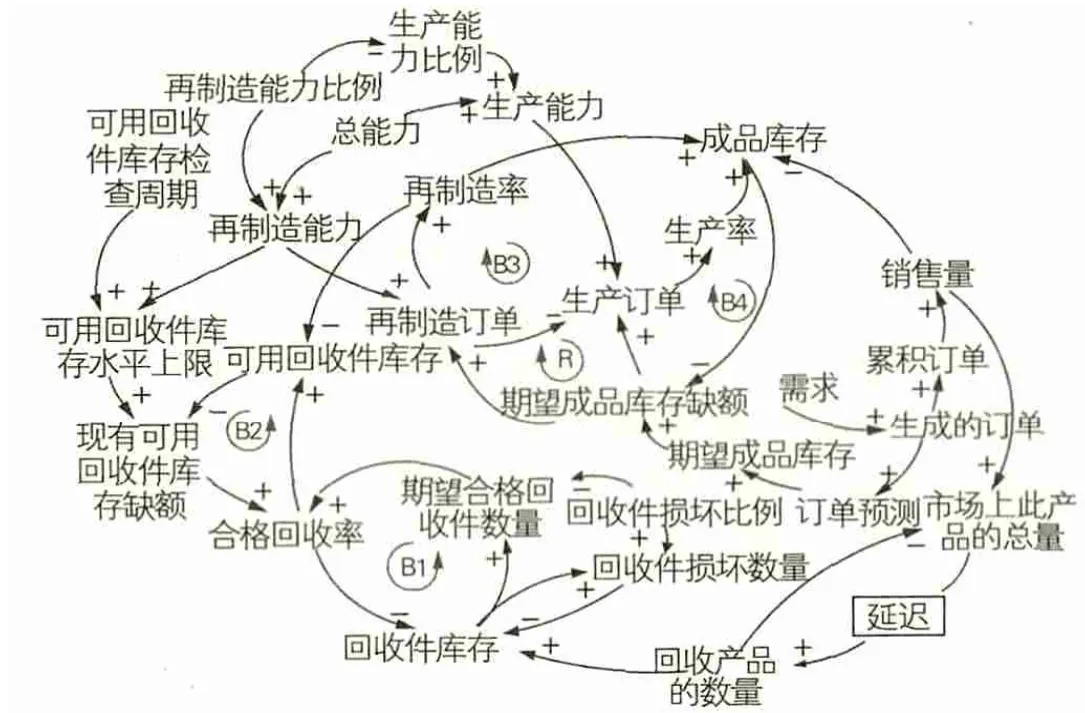
图1 因果回路图

因果图中主要包括4个负反馈回路（B1、B2、B3、B4）和1个正反馈回路（R），B1是回收件库存负反馈回路，B2是可用回收件负反馈回路，B3是成品库存负反馈回路，B4是期望成品库存缺额负反馈回路；负反馈回路总是追求将系统状态保持在目标或设想状态。R是生产订单正反馈回路，它包含再制造订单至生产订单以及成品库存至期望成品库存缺额这两条负因果链，因此它的回路为正；正反馈回路具有将系统的变化加强的作用。系统行为主要是由上述五个反馈回路相互作用而引起，同时系统还包含一个重要的延迟——产品回收延迟，市场上的产品总是需要经过一定的时间才会被制造企业回收。

因果图中的主要关系如下：首先产品的需求使生成的订单数增加，继而通过因果链的传递使期望成品库存增加，然后根据期望成品库存和成品库存计算出期望成品库存缺额，再利用计算出的期望成品库存缺额指导产品的生产和再制造，只有当期望成品库存缺额大于零时企业的生产和再制造活动才会进行。再制造活动的进行还需满足可用回收件库存达到可用回收件库存水平上限这一条件。由于在考虑生产计划方案时优先选择成本较低的再制造，所以再制造对新产品的生产量有反作用[15]，当再制造不能够满足市场的需求时，企业会选择新产品的生产。

四、存量流量图模型

由上节的因果回路图可以给出研究问题的存量流量图，如图2所示。此模型主要由回收、制造、销售三个部分组成。

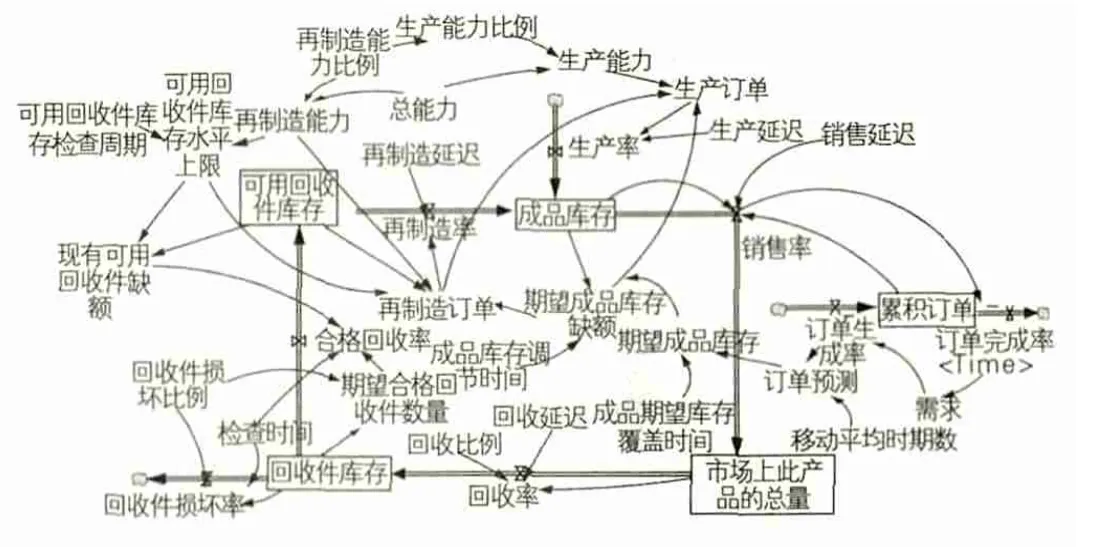
图2 制造企业闭环回收再制造模型

（一）回收部分方程式

产品的回收率由市场上此产品的总量和回收比例所决定，并且要经过一段较长的回收延迟才会进入再制造流程中。回收产品的质量并不一定过关，所以需要检验，不合格的回收件就废弃处理，合格的回收件就进入可用回收件库存。回收件库存的入流量是回收率，其出流量是合格回收率，合格回收率由现有可用回收件缺额和期望合格回收件数量共同决定。有关方程式如（1）-（6）所示。

（二）制造部分方程式

可用回收件库存的入流量是合格回收率，其出流量是再制造率；再制造率是是再制造订单的延迟函数，再制造订单与再制造能力和期望成品库存缺额等有关；期望成品库存缺额是期望成品库存与成品库存的差的延迟函数；成品库存的数量等于生产率加上再制造率减去销售率，其中生产率是生产订单的延迟函数，生产订单则与期望成品库存缺额、生产能力和再制造订单有关；生产能力是生产能力比例和总能力的乘积，再制造能力是再制造能力比例和总能力的乘积；生产能力比例与再制造能力比例之和为1。有关方程式如（7）-（19）所示。

（三）销售部分方程式

销售率与成品库存、累积订单和销售延迟有关；累积订单等于订单生成率减去订单完成率；订单完成率等于销售率，订单生成率则等于需求；订单预测是订单生成率的平滑函数。有关方程式如（20）-（24）所示。

（四）常量设置

常量设置如表1所示。

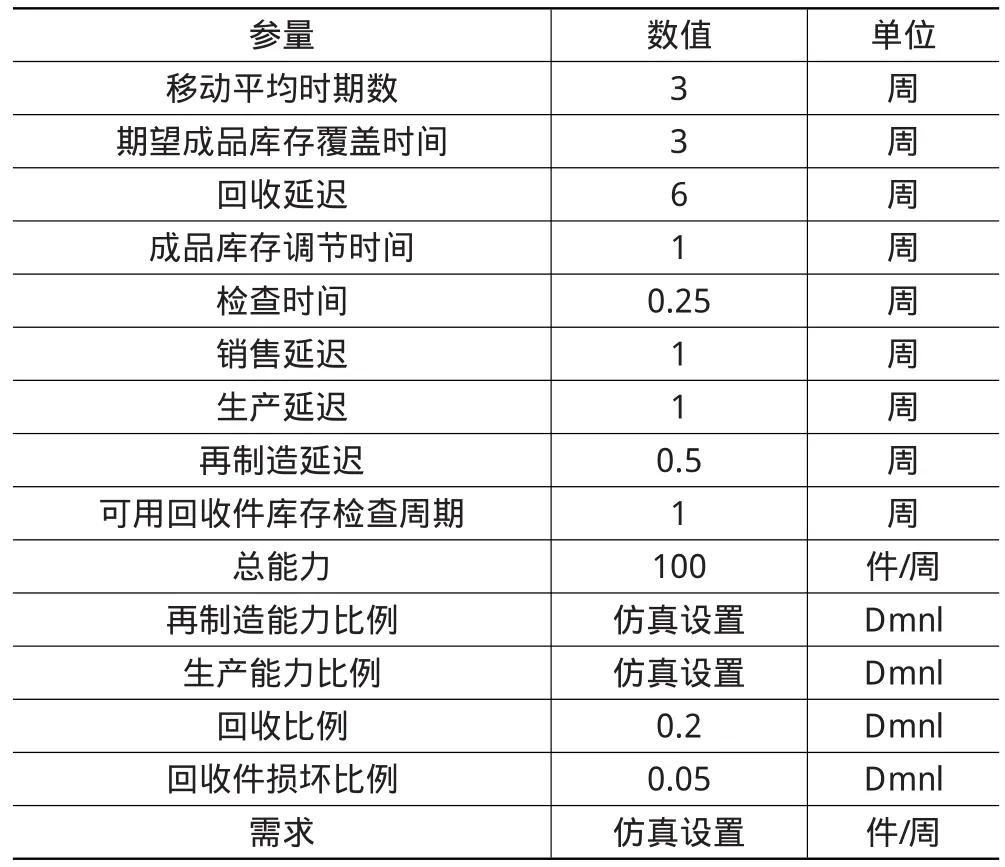
表1 常量设置

五、仿真及结果分析

本文采用Vensim软件对系统动力学模型进行仿真计算。仿真设置：INITIAL TIME=0周，FINAL TIME=100周，表示仿真时间为100周，TIME STEP=0.25周，SAVEPER=TIME STEP。本文将需求分为高需求和低需求两种情况。

高需求下其表达式为：

50+10 × SIN（Time）+RANDOM UNIFORM（10，20，2）+0.1 × Time

低需求下其表达式为：

30+4 × SIN（Time）+RANDOM UNIFORM（4，6，2）+0.1 × Time

其中SIN函数表示需求的季节性，RANDOM UNIFORM函数表示随机性的需求，0.1×Time表示需求的时间性趋势，需求会随着时间而缓慢增长。它们的函数图形如图3所示。

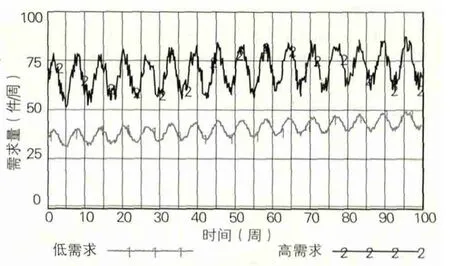
图3 需求情况

（一）高需求下系统行为分析

设置再制造能力比例分别为20%、40%、60%、80%，则生产能力比例分别为80%、60%、40%、20%，固定其他常量不变进行仿真。图4和图5分别表示在高需求情况下再制造能力比例的变化对生产率和累积订单的影响。

图4中的线条1～4表示再制造能力比例分别为80%、60%、40%、20%时，生产率的变化情况。由图4可以看出，在高需求情况下，随着再制造能力比例的逐渐增加，企业的生产率逐渐递减，并且当再制造能力比例达到60%以上时，生产率曲线就变成一条直线，其值是一个固定常数且等于生产能力，表明企业的生产设施达到满负荷运行状态。这说明在高需求条件下，如果企业的再制造能力比例高于某个水平，企业的生产压力会加大以致企业必须满负荷利用再制造设施和生产设施去满足用户的需求。

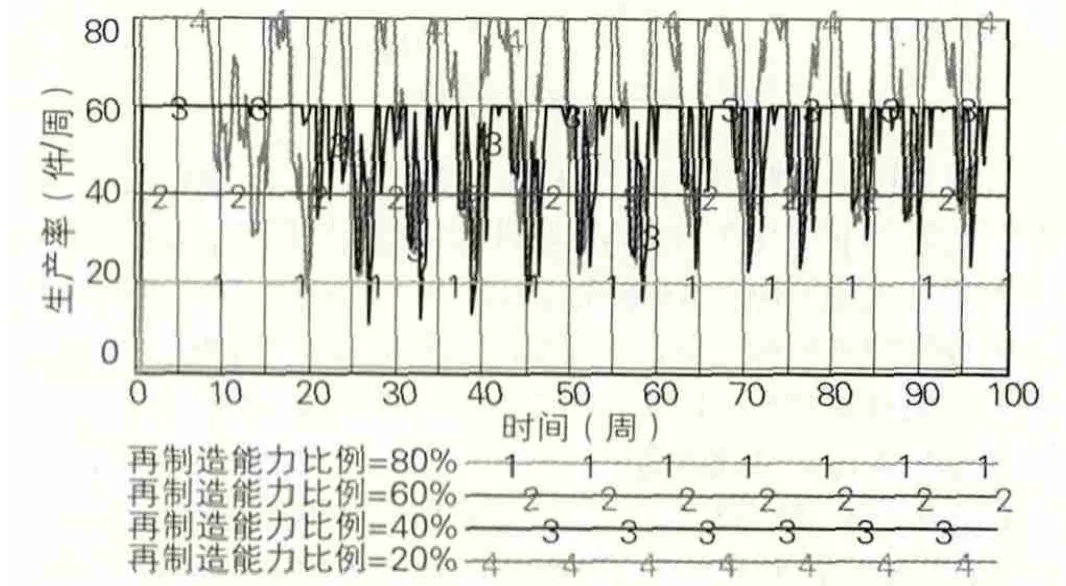
图4 高需求情况下再制造能力比例的变化对生产率的影响

从图5可以看出，在高需求情况下，随着再制造能力比例的逐步升高，累积订单的数量逐渐增加，当再制造能力比例保持在低水平时，如图中所示的20%和40%，累积订单保持在小于100件/周的一个较低的水平；当再制造能力比例达到60%时，累积订单稳定在400件/周这个数量水平上；但是当再制造能力比例达到80%时，累积订单的数量成线性增长，说明企业的生产能力和再制造能力不能满足消费者的需求。出现这种结果主要是因为：过高的再制造能力比例意味着较低的生产能力，而企业再制造活动的进行是有限制条件的，且在仿真之初有6周的延迟，因此在仿真开始和再制造活动停滞时企业只能依靠有限的生产能力去满足高需求，而这必然导致累积订单成倍增长。

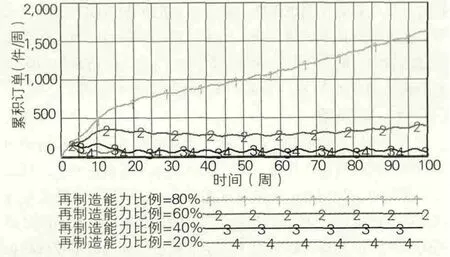
图5 高需求下再制造能力比例的变化对累积订单的影响

（二）低需求下系统行为分析

和高需求情况下一致，在低需求情况下也将再制造能力比例分别设置为20%、40%、60%、80%，则其生产能力比例分别为80%、60%、40%、20%。固定其他常量不变进行仿真。图6和图7分别表示在需求较低的情况下再制造能力比例的变化对生产率和累积订单的影响。

从图6可以看出再制造能力比例为20%、40%，也就是其生产能力比例分别为80%和60%时，这两条生产率曲线的趋势基本一致，且其生产率绝大部分时间都是在60件/周以下，说明其生产设施还没有满负荷运行，企业只需其一部分生产能力即可满足需求；当再制造能力比例为80%，也就是生产能力比例为20%时，其生产设施几乎是满负荷运行，说明制造企业必须尽全力利用生产能力和再制造能力才有可能满足市场需求。

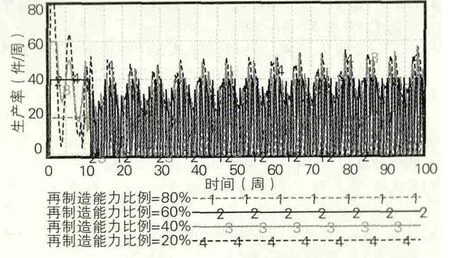
图6 低需求下再制造能力比例的变化对生产率的影响

从图7可以看出，再制造能力比例为20%、40%、60%时，这三条累积订单的曲线几乎重合并稳定保持在较低水平，说明在这三个再制造能力比例下企业可以满足消费者的需求；而当再制造能力比例为80%，即生产能力比例为20%，其累积订单曲线在仿真开始阶段就不断迅速增加并在13周的时候达到顶点217件/周，之后才缓慢下降直到38周后才和前三条累积订单曲线重合并稳定在一个较低的数量水平，之所以出现这种原因是因为：市场上的产品进入回收渠道有一个6周的回收延迟，在这段期间企业不能利用再生产能力生产再制造产品，只能依靠生产能力去生产新产品，而此时生产能力只有总能力的20%，即使满负荷生产也不能满足需求，因此累积订单才会越来越多并在13周达到顶点水平，而在第六周以后，再制造设施开始生产产品，经过一段时间的调整，才会满负荷生产，累积订单由此缓慢减少并在第38周达到较低的稳定水平。

图7 低需求下再制造能力比例的变化对累积订单的影响

（三）两种需求下企业绩效水平分析

为了更好地定量分析回收再制造企业的生产计划与需求之间的关系，本文比较了在高需求和低需求这两种不同的情况下企业再制造能力比例的变化对企业绩效的影响。本文选取企业盈利水平和顾客满意度这两个关键指标来度量企业绩效，企业盈利水平由企业利润额来衡量，而顾客满意度则由缺货率来衡量。缺货率等于缺货的次数除以系统总的仿真次数400次，缺货的次数由累积订单和成品库存所决定。每次仿真时，如果累积订单大于成品库存，系统缺货一次，如果累积订单小于成品库存，系统就不处于缺货状态。当缺货率低于5%时本文认为顾客满意度是比较高的；当其高于5%时顾客满意度则比较低，这时即使企业的利润额较高也不利于企业的长期发展。因此企业理想的绩效水平是：在满足缺货率低于5%的情况下，利润额越高越好。

本文假设企业的成本由库存持有成本、缺货成本、制造成本以及回收成本这四个部分组成，其他成本忽略不计。其中库存持有成本由成品库存持有成本和可用回收件库存持有成本组成；制造成本由再制造成本和生产成本组成；回收成本包括产品的回收、储存和检查等成本。成品库存持有成本为3.5元/件，可用回收件库存持有成本为2元/件，缺货成本为20元/件，再制造成本为20元/件，生产成本为50元/件，回收成本为5元/件。再制造产品和新产品的市场价格均为200元/件。

利用Vensim仿真得到的数据，将其导入至Excel，计算并整理得到高需求和低需求下企业的利润及缺货率，如表2和表3所示。

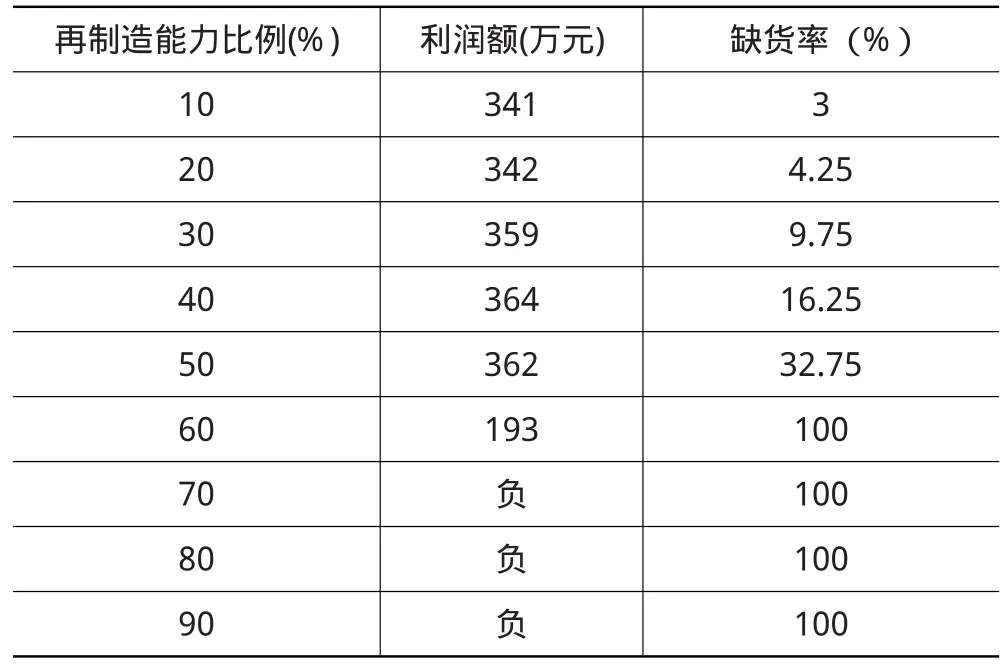
表2 高需求情况下企业利润及缺货率表

表3 低需求情况下企业利润及缺货率表

由表2可知，在高需求情况下，随着再制造能力比例从10%逐步提高至90%，缺货率一直处于增加的趋势并在再制造能力比例=60%时达到100%，这说明随着再生产能力比例的提高，企业的生产设施和再制造设施所生产的产品不能及时满足用户的需求；利润额呈现一个先上升后下降的趋势，在再制造能力比例为40%时利润额达到最大值364万，但此时缺货率已经超过5%达到9.75%，因此再制造能力比例为20%时系统的状态达到最优，此时企业的利润额是342万，缺货率为4.25%。

从表3可知，在低需求情况下，同表2一样，随着再制造能力比例的逐步提高，缺货率也是一直处在增加的趋势中，但增长的幅度非常缓慢，在再制造能力比例=70%时才超过5%；利润额也是呈现一个先上升后下降的趋势，并在再制造能力比例=70%时利润额取得最大值，但在这一点上其缺货率为16%，可知当再生产比例=60%时企业的绩效为最优，此时，利润额为232万，缺货率为4.25%。

由以上分析可以得出，企业在面临高需求量时，应提高企业的生产能力比例以使企业的生产能力大于其再制造能力，虽然再制造成本远小于新产品的生产成本，可是一旦再制造能力比例过高，相应地企业的生产能力比例就会很低，由于企业再制造活动的进行是有条件的，它必须满足可用回收件库存达到可用回收件库存水平上限这一条件，企业在仿真初始阶段或者再制造活动停滞的时候只能依靠企业较低有限的生产能力去满足高市场需求，这样必然使企业的缺货率迅速增加，相应地其缺货成本也会快速增加，进而导致企业总成本的增加。

企业在面临低需求量时，应提高再制造能力比例以使企业的再制造能力大于其生产能力，因为此时需求量较小，尽管企业的再制造活动在仿真开始阶段有一个6周较长时间的回收延迟，但企业较小的生产能力在仿真开始之初仍然能够满足用户的需求，在第6周之后随着企业的再制造活动的进行，企业就可以充分利用成本较低的再制造能力去满足用户的需求；但企业的再制造能力比例也不能过高，过高的再制造能力比例也会导致企业的缺货率成倍增长，因为过高的再制造能力比例意味着过低的生产能力比例，企业过低的生产能力在仿真初始阶段不能满足用户的需求，继而导致企业过高的缺货率。

六、结束语

本文为短生命周期产品的回收再制造提出了基于系统动力学的闭环回收再制造模型，研究了回收再制造企业的生产计划和需求相协调的问题，研究发现在高需求的情况下，企业应提高新产品的生产能力以大于回收产品的再制造能力从而满足市场的需求；而在低需求情况下，企业应尽量利用成本较低的再制造能力以降低企业的成本，也就是企业的再制造能力比例应大于其生产能力比例。其研结果不仅可以为企业安排回收再制造生产计划提供理论指导，还可以辅助制造商在面对外界环境发生变化时（例如回收比例、回收价格以及需求的变动等）做出更好的决策。

本文的仿真模型对现实生活中某些因素做了简化处理，因而必然存在一些不足和局限。如文中假设再制造产品和新产品两者没有任何区别且消费者对它们没有任何的消费偏好，但是在现实生活中消费者有时会比较排斥再制造产品，而比较亲睐于新产品。如何在仿真模型中考虑这一因素有待进一步研究。

[1]姚卫新.再制造条件下逆向物流回收模式的研究[J].管理科学，2004，17（1）：76-79.

[2]赵忠，谢家平，任毅.废旧产品回收再制造计划模式研究述评[J].管理学报，2008，5（2）：305-311.

[3]孔令丞，谢家平，迟琳娜.废旧产品回收再造模式研究[J].理论探索，2008（5）：76-79.

[4]郭军华，李帮义，倪明.不确定需求及WTP差异下的再制造回收模式选择[J].软科学，2012，26（4）：131-135.

[5]李响，李勇建，蔡小强.随机产率和随机需求下的再制造系统的回收定价决策[J].系统工程理论与实践，2009，29（8）：19-27.

[6]彭志强，熊中楷，李根道.基于再制造和顾客等待的差别定价模型研究[J].软科学，2009，23（3）：123-126.

[7]王文宾，达庆利.考虑市场细分的闭环供应链生产与定价策略[J].控制与决策，2009，24（5）：675-679.

[8]孙浩，达庆利.基于产品差异的再制造闭环供应链定价与协调研究[J].管理学报，2010，7（5）：733-738.

[9]包晓英，唐志英，唐小我.基于回收再制造的闭环供应链差异定价策略及协调[J].系统管理学报，2010，19（5）：546-552.

[10]Naeem M A，Dias D J，Tibrewal R，et al.Production planning optimization for manufacturing and remanufacturing system in stochastic environment[J].Journal of Intelligent Manufacturing，2013，24（4）：717-728.

[11]Pan Z，Tang J，Liu O.Capacitated dynamic lot sizing problems in closed-loop supply chain[J].European Journal of Operational Research，2009，198（3）：810-821.

[12 Kiesmüller G P.A new approach for controlling a hybrid stochastic manufacturing/remanufacturing system with inventories and different leadtimes[J].European Journal of Operational Research，2003，147（1）：62-71.

[13]Inderfurth K，van der Laan E.Leadtime effects and policy improvement for stochastic inventory control with remanufacturing[J].International Journal of Production Economics，2001，71（1）：381-390.

[14]Poles R.System Dynamics modelling of a production and inventory system for remanufacturing to evaluate system improvement strategies[J].International Journal of Production Economics，2013，144（1）：189-199.

[15]景熠，王旭，李文川.多重不确定环境下考虑产品差异的再制造批量生产计划[J].计算机集成制造系统，2012，18（12）：2650-2658.

[16]胡海菊，李勇建.考虑再制造和产品需求可替代的短生命周期产品动态批量生产计划问题[J].系统工程理论与实践，2007，27（12）：76-84.

[17]Shi J，Zhang G，Sha J.Optimal production planning for a multiproduct closed loop system with uncertain demand and return[J].Computers&Operations Research，2011，38（3）：641-650.

[18]Georgiadis P，Vlachos D.The effect of environmental parameters on product recovery[J].European Journal of Operational Research，2004，157（2）：449-464.

[19]Vlachos D，Georgiadis P，Iakovou E.A system dynamics model for dynamic capacity planning of remanufacturing in closedloop supply chains[J].Computers&Operations Research，2007，34（2）：367-394.

[20]Shi J，Zhang G，Sha J.Optimal production and pricing policy for a closed loop system[J].Resources，Conservation and Recycling，2011，55（6）：639-647.