连续相位调制解调技术研究
2014-11-20陈静,刘波
陈 静,刘 波
(中国电子科技集团公司第五十四研究所,石家庄050081)
1 引言
近年来,随着军用遥测传输容量需求的迅速扩展,对无线链路传输能力的要求明显提高,虽然PCM-FM在采用多符号检测(MSD)技术后解调误码性能得到了较大的改善[1],但由于其传输速率低、频谱占用宽等缺点,已不能完全满足军用遥测传输容量扩展的需求。因此,寻求性能更为先进的遥测新体制成为研究关注的热点[2]。
为了提高频谱利用率和信息传输速率,在高码率遥测环境下获取更高的解调误码性能,美国的先进靶场遥测计划组织(ARTM)和爱德华兹(Edwards)空军基地(AFB)一起支持Nova公司研究频率利用性能更好的遥测新体制——多指数连续相位调制体制,以期建立起一种新的调制体制,从而取代沿用了数十年的PCM-FM调制体制[3]。连续相位调制(Continuous Phase Modulation,CPM)是一种相位连续、包络恒定的调制体制[4],具有频率利用率高和功率利用率高的优势,可以提供比PCM-FM调制更小的信号带宽。为了适应我国航天航空事业发展的新要求,进一步提高军用遥测系统的频谱利用率和码速率,深入开展该体制的研究具有重要意义。
CPM信号的解调分为相干解调和非相干解调两大类,其中非相干解调早期常用的方案有限幅器-鉴频器法(Limiter-Discriminator,简称LD 法)[5]和 差 分 检 测 法(Differential Detector)[6]。LD法和差分检测法结构简单,但仅限于二进制CPM方案,且由于没有利用到CPM信号相位的内在相关性,检测性能很难达到最佳。1999年,Colavolpe等人给出了 CPM的非相干序列检测算法(Noncoherent Sequence Estimation Algorithm,简称 NSE 算法)[7,8],最大程度的利用了CPM的记忆特性,因此比以前的算法在性能上有了明显提高。但NSE算法为简化复杂度采取了一些近似处理,只能称作准最优最大似然检测算法。
与相干解调相比,非相干解调方案的主要缺点是在信噪比上有较大的损失。在AWGN信道下,CPM信号的最佳解调方法为相干最大似然序列检测[9],其最佳接收机由相关器跟随一个最大似然序列检测器组成。本文针对多进制CPM信号,给出了基于维特比算法的相干接收机方案,从信号状态的具体表示及维特比算法原理出发,讨论了CPM信号的最大似然检测方法,并给出了仿真结果和性能分析。
2 CPM信号模型
2.1 CPM信号形式
CPM是一种有记忆的调制技术,其调制信号可以表示为公式(1)(2)[4]。

其中ES为符号能量,T为符号间隔,ωc为载波角频率,=(α0,α1,…,αn) 是 M 进制符号序列,取值为{±1,±3,…,±(M-1)}。{hi}为调制指数序列,如果对所有符号是固定的,称该CPM信号为单一调制指数CPM。反之,若调制指数从一个符号到另外一个符号时发生变化,称为多调制指数CPM信号。q(t)为归一化相位响应脉冲,是归一化频率响应脉冲g(t)的积分。常用的g(t)有矩形脉冲、升余弦脉冲和高斯脉冲,对应的CPM信号分别记为LREC、LRC和GMSK。
本文主要研究采用升余弦脉冲的CPM信号,g(t)的函数表达式为式(3)。

其中,L为关联长度。L=1时,调制信号称为全响应CPM信号;L为大于1的整数时,调制信号称为部分响应CPM信号。图1是L=2时升余弦脉冲g(t)和q(t)的波形。

图1 升余弦脉冲g(t)和q(t)波形Fig.1 Waveforms of taised cosine pulse g(t)and q(t)
2.2 CPM信号状态
对于具有固定调制指数h的CPM信号,在第n个符号间隔内,即nT≤ t≤ (n+1)T时,式(2)可以重新表示成式(4)(5)。

其中,θn表示nT时刻的相位状态,当调制指数h=m/p(m,p为互质的整数)为有理数时,其状态数目为p或2p;等式(5)右边第一项决定于信息符号 (αn-1,αn-2,…,αn-L+1),称为相关状态,其状态数目为ML-1。因此,对于长度为LT(L>1)的部分响应信号脉冲,CPM信号在t=nT时刻的状态 Sn是由相位状态 θn和相关状态 (αn-1,αn-2,…,αn-L+1) 共同决定的,可以表示为式(6)。

3 CPM信号的最大似然序列检测
3.1 CPM最大似然接收原理
由2.2中的描述可知,CPM是一种有记忆的调制方法,记忆特性来自于一个符号间隔到下一个符号间隔发送载波相位的连续性。对这样有记忆的发送信号,即在连续的符号间隔内发送信号是相互关联的,最佳检测是根据在连续符号间隔内接收信号的观测序列来判决。
假定信号经过一个加性高斯白噪声(AWGN)信道后,接收到的信号为r(t)=s(t,I)+n(t),其中s(t,I)为发送端信号波形,I是实际传送的信息序列,n(t)为高斯白噪声。令为接收端的一个可能的估计序列。CPM的最大似然准则算法的基本思想是:通过状态网格搜索具有最小欧式距离的路径,找到一个可能的估计序列,使得条件概率P|r(t())最大,即在接收到的信号为r(t)条件下,序列具有最大的出现概率。这一准则可以使正确判决概率最大,因此错误概率最小。将似然函数定义为式(7)。

其中,Pn-1(表示直到nT时刻的幸存序列的似然函数,Zn(可表示为式(8)。

表示在nT≤t≤(n+1)T时间间隔内的信号所引起的度量的附加增量,即分支度量。于是,可以用递归的方法产生Pn(),在每个符号间隔内,只需计算其对应的附加度量。
图2给出了最大似然序列检测器结构的示意图,虚线框内为分支度量的计算,即信号经过一组匹配滤波器,匹配结果送入维特比检测器进行解调,然后通过并串转换后输出比特流。

图2 CPM信号最大似然序列检测器结构示意图Fig.2 Block diagram of the maximum-likelihood sequence detector
3.2 维特比算法
在网格图的基础上进行解调就是搜遍网格图找出最可能的序列。然而,如果要对所有可能的序列都进行计算、比较来确定最可能的序列,整个解调的计算量会非常大,尤其是状态数目较多、序列长度较长时,更是难以实现。维特比算法是一种顺序网格搜索算法,可以作为一种有效的解调算法来完成对序列的检测,不仅可以大大减少计算量,而且在解调性能上不会带来损失[10]。
在每个时刻,进入网格节点的每条路径都有自己的度量。维特比算法比较每条路径的度量,存储最大度量的路径,称为幸存路径,用来最后输出与其对应的正确数据序列。在网格图的基础上,维特比算法解调的一般步骤可以概括如下:
1)分支度量计算:在(n+1)T时刻,针对每个状态节点计算进入节点的M个分支度量。
2)路径度量更新:在原有的到达nT时刻的幸存路径基础上用步骤1中得到的分支度量进行路径度量的更新。此时,对于(n+1)T时刻的每个状态节点将得到M个路径度量值。
3)确定幸存路径:对(n+1)T时刻的每个状态节点比较其M个更新后的路径度量值,并保留最大值所对应的路径,同时消去其它M-1条路径。对所有状态节点都完成上述操作后,每个节点将只幸存一条路径。保留幸存路径数据和路径度量数据。
4)获得解调数据:每过一个码元,重复步骤1-3,直到序列结束。然后选出具有最大路径度量的路径,即为最大似然路径,回溯路径所保存的数据,得到解调数据。
需要注意的是,当对一个很长的码元序列进行维特比算法解调时,如果要等到序列结束才能解调出码元序列,则其解调延时对很多实际应用场合来说会太长,用来存储整个序列长度幸存路径的存储器也会太大。同时在计算中发现,当网格图延伸到某一级时,假定为K,在K-d及更早一些时刻,所有幸存序列以概率趋于1而相同。所以这时可以通过设定一个判决延时d来改进维特比算法,即在任意nT时刻,每条幸存路径仅保留最新的d个码元,在每经过一个新的码元间隔后,对各幸存路径度量的大小作比较,找出对应最大度量的幸存路径,在网格图上回退d个码元间隔,将该幸存路径上该时刻的码元判决为解调输出。如果d选得足够大,所有幸存路径在该时刻的码元都相同,改进算法的性能下降可以忽略不计。
4 仿真结果
在这里对CPM信号所做的相干检测仿真,都是基于以下假设:
1)载波同步和码元同步都已经准确建立,即接收机已经准确地知道了载波相位和码元定时;
2)数据传输信道为一个加性高斯白噪声(AWGN)信道。
以部分响应CPM信号为例,选取参数M=2,h=1/2,L=2以及 M=4,h=1/4,L=2的 LRC 信号进行仿真来说明算法的性能。针对不同的判决延时d,仿真得出了维特比算法解调在不同信噪比下的误比特率性能,如图3和图4所示。
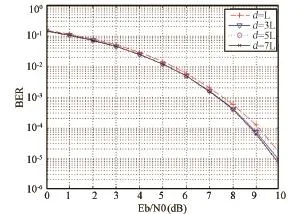
图3 M=2,h=1/2,2RC时误比特率Fig.3 The BER performance with M=2,h=1/2,2RC
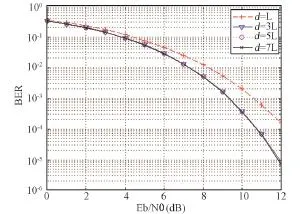
图4 M=4,h=1/4,2RC时误比特率Fig.4 The BER performance with M=4,h=1/4,2RC
由图3可看出,对M=2,h=1/2,g(t)为2RC的CPM信号,判决延时d=3L、5L、7L时误比特率曲线接近重合,而d=L时,在10-3误比特率下解调损失约0.2 dB,在10-4误比特率下解调损失约0.4 dB;由图4 可看出,对于 M=4,h=1/4,g(t)为2RC的CPM信号,判决延时d=5L、7L时误比特率曲线基本重合,d=3L时解调损失很小,而d=L时解调损失较大,在10-3误比特率下已超过1.2 dB。所以,综合考虑解调性能和实际应用中的存储器大小,一般取判决延时d=5L。仿真结果表明,此时解调性能基本没有损失,可以忽略不计。
对当前的PCM-FM遥测体制而言,在10-4误比特率下Eb/N0值为11.4 dB,由图3可以看出,二进制的2RC-CPM信号在10-4误比特率下Eb/N0值约为8.8 dB,其解调性能优于PCM-FM,误比特增益约为2.6 dB;由图4可以看出,四进制的2RC-CPM信号在10-4误比特率下Eb/N0值约为10.7 dB,误比特增益约为0.7 dB,但其传输容量是PCM-FM的2倍。因此,在实际应用中,CPM体制可以根据传输容量和解调性能的需求,灵活地选择合适的进制数与调制指数。与PCM-FM体制相比,CPM体制在频谱利用率和解调性能方面具有明显的优势。
5 结论
本文研究了适用于多进制部分响应CPM信号的相干最大似然序列检测算法,在网格图的基础上采用维特比算法完成信号的解调,并通过仿真分析了算法的解调性能。在载波恢复较为精确的场合,该算法能够得到最佳的解调性能。与传统的PCM-FM信号相比,多进制部分响应CPM信号具有更加明显的带宽和功率效率,将会在通信领域和遥测领域获得越来越广泛的应用。
[1]王晓波,吴岭,徐松艳.MSD与 TPC技术在PCM-FM遥测系统中的应用研究[J].遥测遥控,2007,28(11):49-53.
[2]李秉常,郝建民.多调制指数连续相位调制体制——军用遥测体制的新发展[J].遥测遥控,2002,23(5):1-7.
[3]Geoghegan M.Description and performance results for a multi-h CPM telemetry waveform[C]//IEEE,2000,0-7803-6521-6:353-357.
[4]Anderson J.B.,Aulin T.,Sundberg C.E.Advance in constant envelope coded modulation[J].IEEE Commun,1991,29(12):36-45.
[5]Torrieri D.J.Frequency hopping with multiple frequencyshift keying and hard decisions[J].IEEE Trans:Communications,1984,vol.COM-32:574-582.
[6]Kaleh G.K.A differentially coherent receiver for minimum shift keying signal[J].IEEE Journal on Selected Areas in Communications,1989,7(1):99-106.
[7]Colavolpe G.,Raheli R.Noncoherent sequence detection[J].IEEE Transactions on Communications,1999,47(9):1376-1385.
[8]Colavolpe G.,Raheli R.Noncoherent sequence detection of continuous phase modulations[J].IEEE Transactions on Communications,1999,47(9):1303-1307.
[9]曾佐祺,李赞.基于Viterbi算法的GMSK信号解调性能分析与仿真[J].重庆邮电大学学报,2008,20(2):132-138.
[10]Lin Z.,Aulin T.New lower bounds on symbol error probability for MLSD of CPM signals on AWGN channel[J].IEE Proceedings online,2003,150(5):312-316.
