一种基于条件生成对抗网络的高感知图像压缩方法

2022-07-08张雪峰许华文杨棉子美

东北大学学报（自然科学版） 2022年6期

张雪峰, 许华文, 杨棉子美

(东北大学理学院, 辽宁沈阳 110819)

随着多媒体技术及计算机硬件性能的跨越式发展,图像在信息传递过程中发挥着愈来愈重要的作用.同样的信息,文字表达篇幅冗长,图像往往更为生动形象和直观.为了高效地存储图像,有损图像压缩算法在许多实际场景都有应用.

最广泛使用的有损图像编解码算法之一是JPEG[1].它把图像分割成小块,并且使用离散余弦变换对图像数据进行编码.然后将得到的系数进行缩放、量化和熵编码以形成最终的比特流.对于比较新的编码格式,工业界在诸多不同的方向进行了探索研究,如使用其他变换——JEPG2000[2]中的小波或内部预测,而BPG(better portable graphics)[3]和WebP[4]则是使用了来自视频编解码器HEVC(high efficiency video coding)[5]的环内过滤.

近些年来,深度学习工具在计算机视觉领域得到了比较广泛的应用,基于深度学习的有损压缩算法不断地被提出.这些模型不需要人工设计编解码器的各个组成部分,而是可以从图像数据中深度学习得到一个最佳的非线性变换,然后以端到端的方式将熵编码成比特流,人们在其中直接使用神经网络来进行优化香农提出的比特率-失真权衡.早期的研究依赖于循环神经网络[6-7],而后续的研究则是基于自动编码器[8-10].为了降低存储图像所需的比特率,人们尝试使用各种方法来更精确地建模自动编码器隐藏层的概率密度,以实现更有效的算术编码.采用的方法包括使用分层先验、具有各种上下文形状的自动回归或将二者结合[11-14].目前,最新的模型在峰值信噪比(PSNR)指标上优于BPG,例如Minnen等[15]的研究.

自从Goodfellow等[16]提出生成对抗网络后,它在无条件和有条件的图像生成方面均快速发展.现今最先进的生成对抗网络可以生成高分辨率的逼真图像[17-19].相较于传统的方法[20-21],生成对抗网络在图像分割[22]、图像去噪[23]等应用中也取得了进展.此外,生成对抗损失也被用来改善神经网络压缩算法的视觉质量[14,24-26].Rippel等[14]在全分辨率压缩算法中使用生成对抗损失作为损失函数的一个组成部分,但是并没有系统地最小化这类损失,也没有研究这类损失对于压缩质量的影响.Tschannen等[24]和Blau等[25]则侧重于以概念上合理的方式将生成对抗损失纳入比特率-失真指标当中.具体而言,Tschannen等[24]提出使用分布约束来作为比特率-失真指标的一部分,以确保压缩图像的分布在所有比特率下都与原始图像的分布相吻合;Blau等[25]则提出并研究了比特率-失真-感知之间的三重权衡.Agustsson等[26]提出了使用生成对抗网络来防止压缩伪影,还验证了在很低的比特率下使用基于生成对抗网络的压缩算法可以节省两倍于传统算法的比特率.他们提出的压缩模型可以在极低的比特率下生成视觉感知上十分细腻的压缩重建，但压缩所得的图像往往只保留高级的语义,与原始图像有较大的偏差.

针对上述问题,本文提出一种基于条件生成对抗网络的图像压缩算法,使用条件生成对抗网络来优化深层卷积神经网络.生成器中采用通道归一化层替代实例归一化,对各个通道进行归一化处理,有助于缓解暗化伪影的问题[27].在损失函数方面,使用预训练好的VGG-16网络激活前的特征值来计算感知损失,以实现压缩图像的细腻纹路细节重建.最后,在训练过程中加入生成对抗损失,以提升压缩精度.

1 基于条件生成对抗网络的图像压缩

1.1 图像压缩模型

给定原始图像x,希望对其进行压缩,而不是存储原始的RGB数据.首先需要对其进行编码,为此需要设计一个编码器E,记编码后的隐变量为y=E(x),接着需要对编码的y进行存储,而存储则是经由概率模型P和熵编码(如算术编码)实现,忽略熵编码增加的比特率,记无损存储y的比特率为r(y)=-log(P(y)).为了得到压缩后的图像x′,需要设计一个解码器G对y进行解码,记为x′=G(y).原始图像与压缩重建图像之间的差异记为失真d(x,x′).将E,G,P参数化为卷积神经网络,那么本文的目标转换训练网络使得以下比特率-失真权衡最小化:

LEG=Ex～pX[λr(y)+d(x,x′)].

(1)

其中λ为控制参数.

在上述基于神经网络的有损压缩算法的基础上,本文引入条件生成对抗网络[28]进行优化,其由有约束的生成器G(也就是解码器)和判别器D组成.生成器试图将编码量化的数据变换为逼近原始图像的压缩重建图像,而判别器则试图区分压缩重建图像与原始图像之间的差异.总体模型框架如图1所示.

图1 HIPC模型结构图Fig.1 The architecture of HIPC

1. 2 各个网络结构设置

1.2.1 编码器架构和概率模型及量化

编码器、生成器、判别器的架构借鉴自文献[26,29],其中编码器的架构如图2所示.卷积核除图中特殊说明以外,均采用3×3的大小.Conv60表示卷积层中滤波器的数量或者输出空间的维数为60,其余类似解读.↓2表示进行卷积步长为2的下采样,而Norm表示通道归一化(channel normalization),有关归一化详见1.2.3节,ReLU是常用的激活函数(后同).编码器首先采用了5个各异的卷积层进行图像特征的提取,之后本文在编码器最后一层引入一个瓶颈层ConvCy以避免过拟合.对于概率模型,本文使用文献[11]中提出的超先验概率模型,用于剔除图像压缩过程中的冗余信息.对于待压缩图像,无法知道其实际分布,只知道它的分布是存在统计依赖关系的.为了模拟目标变量之间的依赖关系,该模型引入一组额外的随机变量进行描述.具体来说,将边信息视为熵模型参数的先验信息,从而使它们成为潜在表示的先决条件.提取边信息z来建模y的分布以便于存储,并在超编码器当中以及估计p(y|z)使用均匀噪声U(-1/2,1/2)来模拟量化.但是,当将y输入到G时,本文使用四舍五入代替了噪声,这确保了生成器在训练过程中量化噪声是相同的.

图2 编码器架构Fig.2 The architecture of encoder

1.2.2 生成器及判别器架构

生成器的架构如图3所示,↑2表示进行卷积步长为2的上采样.与编码器相比较,本文在生成器中引入了残差模块.对于编码量化后的隐变量y,采用了9层残差层进行解码,其后提取其中的特征用于压缩重建图像的生成,与编码器类似,最后加入了瓶颈层防止过拟合.

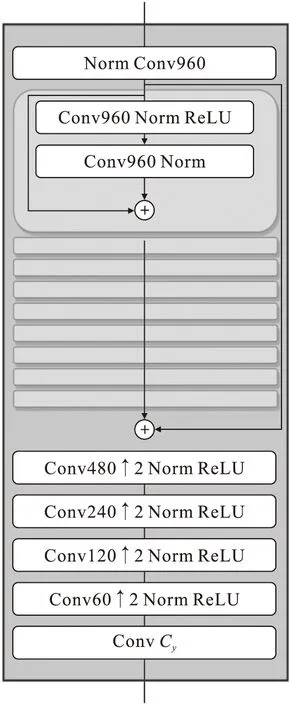
图3 生成器架构Fig.3 The architecture of generator

判别器的架构如图4所示,NN↑16表示进行16×16的上采样调整.部分卷积层中采用的激活函数LReLU,其中参数取α=0.2.最后一层采用1×1的卷积核并施加Sigmoid激活函数以得到判别结果.文献[26,29]中都使用了多尺度马尔科夫判别器,但本文仅使用单一尺度,并且本文使用了谱归一化(spectral normalization)取代实例归一化(instance normalization).谱归一化的具体实现如下:

图4 判别器架构Fig.4 The architecture of discriminator

谱归一化即为参数矩阵W除以W的谱范数.若想求得W的谱范数,需计算得到矩阵的奇异值,但计算量较大,所以使用“幂迭代法”近似计算.先随机生成高斯初始化向量.再按从上到下的顺序计算下式:

不断重复迭代上两式,直到循环k次结束迭代.σ(W)表示矩阵W的最大奇异值,最后得到σ(W)=(uk)TWvk.

在迭代次数足够多时,uk为W最大奇异值的相应的特征矢量,所以有WWTu=σ(W)u,即可求得矩阵W的最大奇异值.

1.2.3 归一化

在文献[26]中,编码器和生成器也使用了实例归一化,但文献[27]发现当在分辨率与训练裁剪大小不同的图像上使用该模型时,会产生明显的暗化伪影.他们假设这是由于实例归一化的空间平均引起的,并且采用通道归一化缓解了这个问题.基于此,本文使用通道归一化,它可以对各个通道进行归一化.假设输入的是一批C×H×W维卷积输出层fchw,使用学习得到的每通道偏移量αc,βc,则可以将其归一化为

(2)

其中:

(3)

(4)

1.2.4 损失函数

条件生成对抗网络可以学习得到符合条件分布pX|S的生成模型,其中每个数据点x与附加信息s(例如类标签或语义映射)相关联,x,s通过未知的联合分布px,s相关联.与标准的生成对抗网络类似,在这种情况下,本文训练两个相互博弈的网络: 一个条件生成器G,其将样本y从一个固定的已知分布pY映射到pX|S; 一个判别器D,它的作用是将输入(x,s)映射到pX|S的一个样本概率,而不是生成器的输出概率.生成器的目标是使判别器相信它的样本是真实的,也就是说,来自于pX|S.固定s,可以优化“非饱和”损失函数[16]:

LG=Ey～pY[-log(D(G(y,s),s))] ,

(5)

LD=Ey～pY[-log(1-D(G(y,s),s))]+
Ex～pX|S[-log(D(x,s))].

(6)

本文采用DISTS[30]作为感知失真dP=DISTS,其灵感来自于感知失真指标LPIPS[31].x为原图像,z为失真后的图像,通过卷积核f:n→r,把x和z分别映射到和和分别表示x和z输入VGG中第i层的的第j个卷积核卷积的输出,其中和分别表示和的均值和方差αij和βij为学习的参数.dP的具体定义如下[30]:

由于模型的高感知特性,本文将其命名为高感知图像压缩算法HPIC(high perceptual image compression).文献[27]验证了采用VGG的损失函数有助于模型的训练,DISTS正是基于文献[30]的VGG-16网络所得.因此本文将DISTS与MSE组合到一起作为失真损失:

d=kMMSE+kPdP.

(7)

其中，kM,kP是超参数.结合神经网络的损失函数式(1),在式(5)和式(6)中令y=E(x)以及s=y.利用式(7)先训练编码器得到初始模型,再引入对抗生成网络,其中式(8)和式(9)分别用来训练生成器和判别器.在训练其中一个时,固定另外两个的参数生成,使用相应的损失函数,交替进行训练,即如果训练生成器时,固定编码器和判别器的参数.判别器分别输入解码得到的x′,编码得到的y和原图像x,y得到D(x′,y)和D(x,y).本文所采用的损失函数如下:

LEGP=Ex～pX[λr(y)+d(x,x′)-
βlog(D(x′,y))] ,

(8)

LD=Ex～pX[-log(1-D(x′,y))]+
Ex～pX[-log(D(x,y))] .

(9)

2 实验结果与分析

2.1 实验参数设置

本文采用微软的COCO[32]数据集作为训练集,训练中将这些图像随机裁剪到256×256像素.模型训练完成后,本文利用独立于训练数据集的基准数据集Tecnick[33]对所得到的模型进行评估与比较,以验证本文模型的效果.

当采用式(1)作为损失函数来训练模型时,式中只有一项失真d(x,x′)与比特率项r(y)有冲突,此时模型的最终(平均)比特率可以只通过变化来控制.但考虑到本文所采用的损失函数式(8)中,MSE,dP=DISTS以及log(D(x′,y))均与比特率项不一致.对于固定的或者不同的超参数kM,kP,将会导致模型具有不同的比特率,使得比较变得困难.为了缓解上述情况,本文引入一个“目标比特率”超参数rt,并将式(8)中的参数λ替换为自适应项λ′,引入两个超参数λ(a),λ(b)将其定义如下:

(10)

其中，λ(a)>>λ(b),这使得训练所得模型的比特率接近“目标比特率”rt.此外,本文使用Adam优化器进行训练.本文中模型使用的参数以及训练策略如表1和表2所示.

表1 固定参数设置Table 1 Fixed parameter settings

表2 变化参数设置Table 2 Change parameter settings

为了使模型能更好地接近目标比特率,在初始训练时采用更高的比特率(相应的自适应项参数也调整为目标比特率的两倍)进行训练,到达一定的步长后再调整为目标比特率.对于学习率而言,损失函数下降到局部最优值之后进行裁剪来优化训练过程.

为了验证加入生成对抗网络的效果,本文训练了一个无生成对抗网络的基准模型,也采用MSE和DISTS作为损失函数.此外,本文与文献[11]中的bmshj2018模型以及文献[15]中的mbt2018模型进行了对比,后者与本文采用相同的超先验概率模型.而为了得到本文的高感知模型,首先训练一个初始模型,采用MSE和DISTS作为损失函数.之后的高感知模型基于上述模型进行初始化,加入生成对抗网络的损失函数,而不是从0开始初始化,具体的训练策略如表3所示,其中k表示1 000.

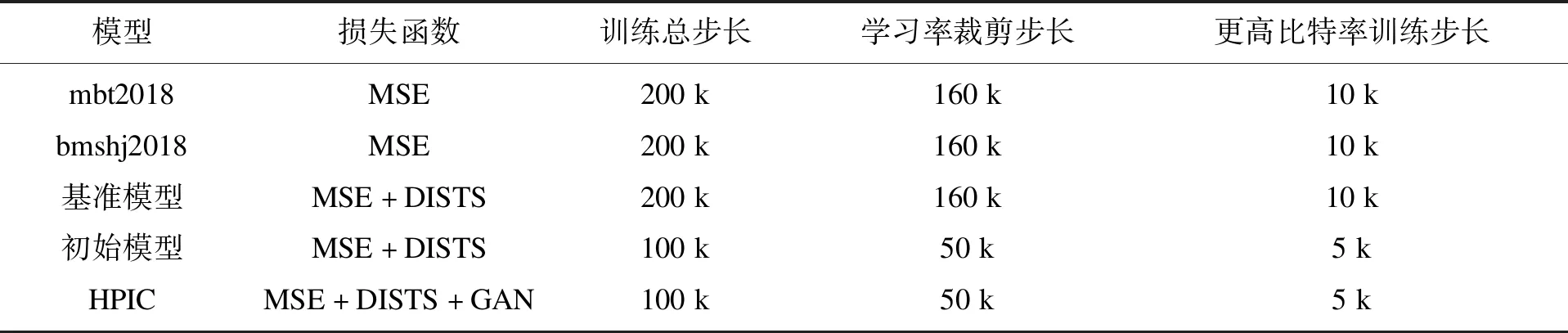
表3 训练策略Table 3 Training strategies

2.2 模型评价指标

本文计算训练得到的各个模型的PSNR以及感知失真DISTS和MS-SSIM,并且采用FID[34]和KID[35],LPIPS作为感知质量指标.峰值信噪比PSNR是图像处理领域最常用的评价指标,而多尺度结构相似性MS-SSIM是评估(和训练)神经网络压缩算法最广泛使用的失真指标.DISTS与LPIPS类似,它可以测量最初训练用于图像分类的深层神经网络的特征空间中的距离,但也适用于预测压缩像素块的相似性,其经过验证可以预测这些形变的视觉感知得分[30].

FID是一种广泛使用的指标,用于评估图像生成(尤其是生成对抗网络)中的样本质量和多样性.与PSNR,MS-SSIM和LPIPS分别测量单个图像对之间的相似度不同,FID则是评估原始图像分布与生成的或失真的图像分布之间的相似性.这种相似性是在为图像分类所训练的 Inception 网络的特征空间中测量的,方法是对特征进行高斯拟合,并计算参考图像的概率分布函数与生成图像的概率分布函数之间的 Wasserstein 距离.Heusel 等[34]验证了FID与失真的增长及用户感知是一致的.此外,经过验证它还可以用来检测常见的生成对抗网络失效模式,如模式下降和模式崩溃.KID 与FID是类似的,但不同之处在于KID是无偏的,并且不对特征空间中的分布做任何假设.

2.3 可视化结果

本文训练的模型效果如图5所示,将所得到的模型与相同比特率的mbt2018模型、BPG模型以及两倍比特率的BPG模型进行了比较.当采用BPG模型进行压缩时采用最高的 PSNR 设定,即无色度二次采样和“慢速”模式.可以看到,基于生成对抗网络的模型生成了非常接近输入的高感知压缩重建,包括毛发与皮肤纹理,而BPG则出现了块状伪影,如图6所示,而且这些伪影是以两倍的比特率出现.

图5 各模型压缩效果Fig.5 Compressed images of each model(a)—原图； (b)—HIPC(0.15 bpp)； (c)—BPG(P.30 bpp); (d)—mbt2018(0.14 bpp); (e)—bmshj2018(0.16 bpp).

图6 压缩细节对比Fig.6 Comparing of texture detail(a)—原图； (b)—HIPC(0.15 bpp)； (c)—BPG(P.30 bpp); (d)—mbt2018(0.14 bpp); (e)—bmshj2018(0.16 bpp).

在测试数据集上采用了上文所叙述的6个指标作为纵坐标,以每像素比特率bpp(bits per pixel)作为横坐标,在图7和图8中分别画出了比特率-感知和比特率-失真曲线(其中↓表示指标越小越好,↑表示指标越大越好).将本文的模型与基准模型(无生成对抗网络)、mbt2018模型、bmshj2018模型以及BPG模型进行了对比.

如图7所示,正如预想中的那样,本文的高感知模型HPIC在所有感知质量指标中处于领先,但 PSNR指标和MS-SSIM指标相对较差.把具有相同的失真的基准模型(无生成对抗网络)与HPIC进行比较,结果表明增加生成对抗网络损失的效果与理论相符，所有感知指标都得到了改善.而且HPIC在所有感知指标上的表现都要优于以往的模型.

图7 各模型的比特率-感知曲线Fig.7 Bit rate-distortion curves of each model(a)—比特率-FID曲线； (b)—比特率-KID曲线； (c)—比特率-DISTS曲线； (d)—比特率-LPIPS曲线.

从图8基于MS-SSIM和PSNR指标的比特率-失真曲线可以观察到,与DISTS等感知指标相比,基准模型与HPIC在这两个失真指标中的表现各异.加入生成对抗网络使得模型的PSNR稍微变差,但MS-SSIM却略有提高,这与参数设定有关.而与bmshj2018和mbt2018模型相比,HPIC模型的PSNR指标都有一定程度下降,但如图7所见,HPIC模型的所有感知指标相较于前两者得到了大幅提升,这说明牺牲一定的数据保真度以换取更好的人类视觉感知质量是可行的.上述结果促使本文在进行灵敏度分析时使用KID等感知指标,只需要在固定失真的损失函数以及整体训练设定的条件下进行对比.

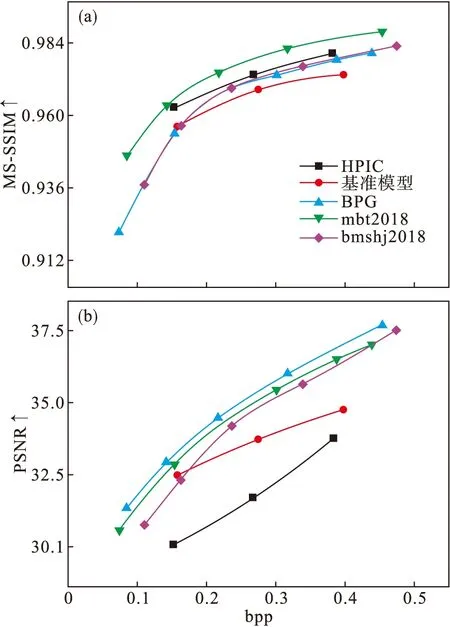
图8 各模型的比特率-失真曲线Fig.8 Bit rate-perception curves of each model(a)—比特率-MS-SSIM曲线； (b)—比特率-PSNR曲线.

总体而言,基于Blau等[25]提出的“比特率-失真-感知”权衡理论,在一个固定的比率下,更好的感知质量总是意味着更糟糕的失真.相反,当最小化失真时就会使得感知质量变得较差.本文通过引入生成对抗网络,使得输入分布和压缩重建分布之间的差异尽量减少,以取得更好的感知质量,但三者仍是不可兼得的.实验结果表明本文的方法相较于以往的方法而言,在三者之间取得了较好的平衡,且实现了高感知质量的图像压缩.