动态子结构方法在全箭动特性分析中的应用研究

张 忠，韩 丽，任 方，李海波，秦朝红

(北京强度环境研究所可靠性与环境工程技术重点实验室，北京100076)

1 引言

运载火箭全箭动力学特性是姿态控制系统设计、载荷分析、POGO分析等的基础和依据，全箭动特性建模和分析是必不可少的［1］。运载火箭的结构变得越来越复杂，呈现出空间模态特征，仅仅依靠传统的梁模型无法很好的反映其动力学特性，需建立复杂的三维模型，导致相应的计算成本增加，有时所建立的有限元模型甚至会有上百万个自由度，如何提高计算效率成为解决该问题的关键。子结构模态综合法是解决大型复杂结构特征值计算问题的有效方法，模态综合法将整个系统划分为多个子结构，每个子结构独立建模，然后再组配成整体结构，其优点是可以缩减系统自由度，提高计算效率。根据子结构界面约束条件的不同，可以把子结构位移表达式分为三类:①自由界面模态综合法［2-6］;②约束界面模态综合法［7-10］;③混合界面模态综合法［3，11］，邱吉宝对模态综合法进行了系统的研究，并在文献［11］中对动态子结构法进行了总结。

运载火箭贮箱内装有的液体燃料，约占运载火箭质量的80%，液体建模的正确与否直接影响全箭动力学建模的准确性。目前工程上液体建模多采用集中质量方法和虚质量方法［12］。集中质量方法可应用于运载火箭梁模型或三维模型，将液体当作单纯的集中质量处理，其缺点是无法反映液体运动与贮箱的柔性变形之间的耦合关系;为了解决集中质量建模的问题，大型有限元软件NASTRAN提供了液体虚质量建模方法，但工程上应用不多，其主要原因是虚质量建模会给出一个与贮箱自由度规模相当的满质量阵，导致计算效率大大降低，甚至无法进行大规模模型的计算。

为了解决上述问题，本文提出了采用动态子结构和虚质量相结合的方法，在保证计算精度的同时降低了求解规模，提高了计算效率。

2 基本理论

2.1 虚质量方法

虚质量建模是建立在液体无旋、无粘、不可压假定之下的，液体的作用最终转化为附加到贮箱壁上的附加质量，这些附加质量的计算并不是按照液体的实际质量，而是按照液体运动方程，将液体内部的运动方程转化到边界上，最终形成一个边界自由度上的质量阵，虚质量建模方法能够克服集中质量方法的弊端［12］。

假设流体是无粘、不可压缩的理想流体，流场是拟静态场，结构是线弹性小变形结构，根据流体力学模型，利用Helmholtz方法求解Laplace方程，借助边界元方法离散技术进行数值求解，可获得液体对结构的集中质量。

液体速度势及压力场如公式(1)(2)所示。

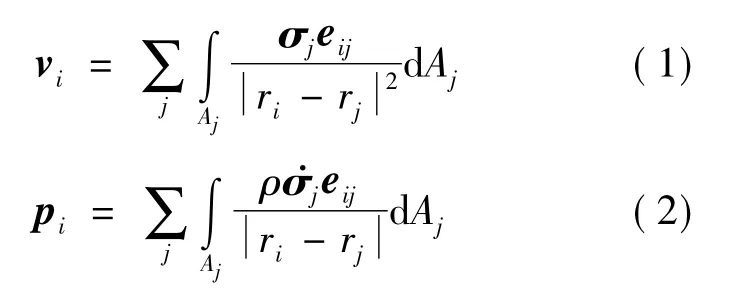
式中，vi——任意结点ri处速度向量;

pi——任意面Aj上的压力;

Aj——结构体表面上微元面积;

σj——j结点处的流速向量;

eij——从j点到i点的单位向量

ρ——流体密度

ri——结点位置

将式(1)及式(2)积分得到公式(3)(4)。

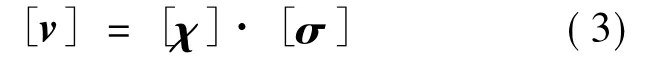
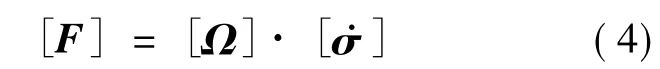
附加质量阵如式(5)所示。

获得附加质量后，质量矩阵会变成一个相对满的阵，这给求解特征值问题带来一定的困难，需采用动态子结构方法进行模型缩减。

2.2 动态子结构模态综合方法

考虑液体附加质量后的结构动力学方程如式(6)所示。

其中，M ＝M0+MA，M0为结构质量阵，MA为液体附加质量阵，K为刚度阵，F为载荷向量。

将动力学方程按保留自由度和非保留自由度分块后得式(7)。

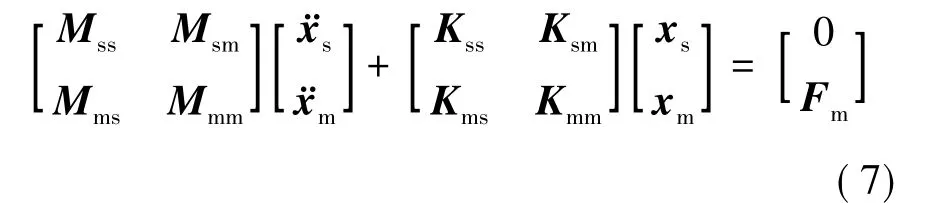
式中，下标m、s分别代表交界面和非交界面自由度，并且对于求解系统的特征值问题，除了界面约束力Fm外，没有其他任何力，即Fs=0。

约束模态综合法的子结构坐标变换矩阵由边界约束的子结构主模态以及约束模态组成。由模态展开定理可以得到式(8)。

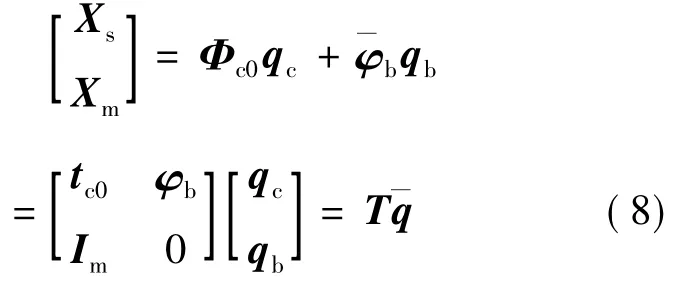
将式(7)代入式(6)，并前乘TT可以得到以模态坐标描述的刚度矩阵、质量矩阵、模态力向量如式(10)～(12)所示。

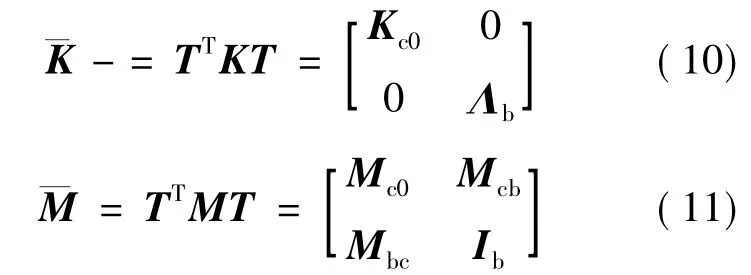
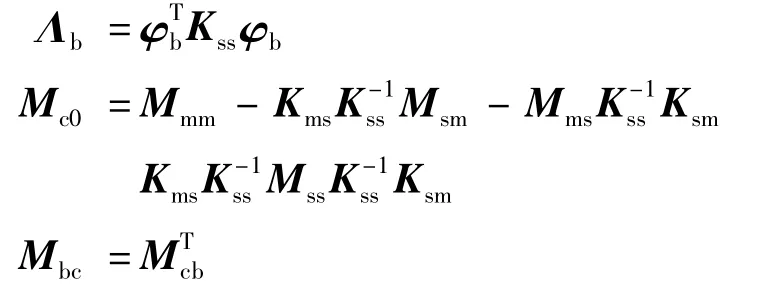
式(13)即为包含所需低频模态信息的动力学方程。通过以上一系列的求解，有限元模型的自由度大大减少。

可以将广义模型当作物理模型一样看待完成耦合分析。耦合分析过程是根据各子结构交界面的位移和力的协调条件完成整体耦合结构运动方程的组装，然后求解整体运动方程的动力学问题。

两个独立子结构a、b的动力学方程根据式(13)，可以写成式(14)～(15)。

采用Excel 2013软件建立数据库，通过SPSS19.0统计软件进行数据处理，检验水准取p=0.05，所有数据均以±sd表示。采用单因素方差分析(one-way ANOVA)，方差齐时组间比较采用Duncan法，方差不齐时组间比较采用DunnettsT3法。p＜0.05为差异有统计学意义。

可以将广义模型当作物理模型一样看待，应用式(16)(17)所示的协调条件和平衡条件

得到组合体的整体动力学方程为如式(18)所示。

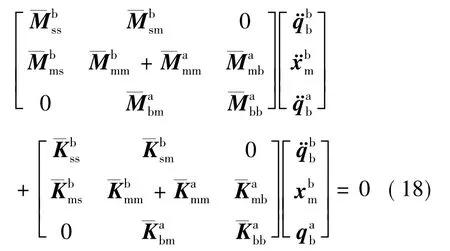
式(18)即为耦合系统的整体动力学方程，求解(18)时即可得到整体耦合系统的模态信息。

对于多级子结构耦合分析，只需按照以上步骤依次进行计算即可。

3 算例分析

3.1 全箭结构有限元建模与分析

有限元模型主体结构采用梁—壳三维模型，推进剂采用集中质量进行模拟，只计质量，不计转动惯量，并通过RBE3与贮箱壳单元连接;助推与芯级连接采用梁(杆)单元进行模拟，并释放旋转自由度模拟铰接;发动机采用等效梁单元模拟，所建立的有限元模型如图1所示。

图1 有限元模型Fig.1 FEM model

首先，开展不包含液体推进剂的动态子结构模态综合计算分析。对于运载火箭和航天器组成的系统级模型，通过在星箭界面施加固定界面约束将该系统分成两部分，分别作为运载火箭子结构和航天器子结构，保留航天器和运载火箭子结构的低阶模态，运用上述动态子结构法进行综合，得到整体结构的计算结果，并与整体有限元解进行比较，验证其计算精度。

模态综合计算结果与整体有限元模型计算结果对比列入表1中。从表1中可以看出，在低频范围内，具有较高的计算精度。除了计算精度外，计算效率也是工程广泛关注的一个问题。对于本算例，整体有限元模型具有30多万个自由度，而经过一系列缩聚后其模态综合模型的自由度不足1000个，计算效率的提升是不可言喻的。

表1 不同方法模态频率计算结果对比Table 1 Comparison of modal frequencies obtained by different methods

3.2 考虑液体推进剂的全箭模态计算分析

本文采用动态子结构法+虚质量缩聚方法来降低自由度数目，进行了全箭的液体推进剂虚质量模拟方法研究。首先，将芯二级、芯一级、助推器的氧箱、燃箱提交计算生成广义模型，然后采用超单元的方法将广义模型与级间段、箱间段等其余部分有限元模型进行耦合分析，得到全箭动特性，最后与传统集中质量方法进行对比。

对单独助推器的零秒状态进行了模态计算。如图2、图3所示，通过弯曲模态的对比发现，两种计算方法的计算结果虽有一定的差异，但是均在工程接受范围之内。但是通过图4的纵向模态对比发现，两种方法在计算结果差异较大，传统方法计算得到的纵向模态要明显高于虚质量法。这是因为根据液体推进剂无粘性的特性，贮箱横向弯曲变形时，除自由液面附近的推进剂外，其余大部分推进剂跟随箭体结构一起平动，以上两种方法均满足此假设，因此计算结果一致。而在纵向变形时时，推进剂仅跟随箱底运动，虚质量法对液体推进剂运动的模拟与实际情况相符。而传统RBE3液体推进剂质量建模方法相当于液体质量沿贮箱纵向均匀分布并随箱壁一起运动，与实际情况不符，因此计算结果误差较大。

集中质量方法将液体当作单纯的集中质量处理，虚质量方法对附加质量的计算并不是按照液体的实际质量，而是按照液体运动方程，将液体内部的运动方程转化到边界上，最终形成一个边界自由度上的质量阵。虚质量法对液体推进剂的模拟更加真实，克服了集中质量方法的弊端。

图2 助推器一阶弯曲模态Fig.2 1st bending mode of booster

图3 助推器二阶弯曲模态Fig.3 2nd bending mode of booster

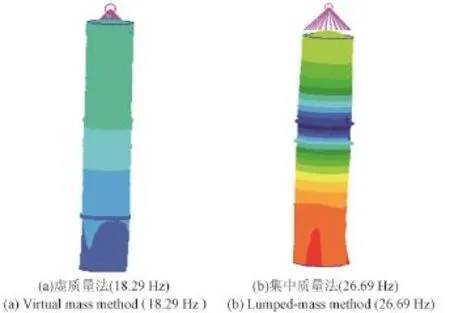
图4 助推器一阶纵向模态Fig.4 1st Longitudinal mode of booster

采用虚质量方法对全箭的动特性也进行了计算，计算结果列入表2中，从表中可以看出，与单独助推器计算得到的结论有所不同，两种计算方法得到的全箭模态结果基本一致，甚至纵向的计算结果也基本一致。这与全箭的质量特性和模态形状有关，纵向模态如图5所示，其模态形状主要表现为助推器的上下运动，并且其纵向变形很小，推进剂耦合效应不明显，此时助推器纵向表现为整体质量效应，两种方法的对液体质量的描述均合理，因此得到的计算结果一致。

通过以上讨论可以看出，采用不同方法计算结果的差异与所关心的模态形状、液体表现出的质量特性有关。如果液体质量的耦合效应不明显，集中质量方法可以作为虚质量法的一个特例，此时两种方法计算得到的结果一致(如全箭动特性的计算)，为了简化可以采用集中质量方法进行计算。但是，如果耦合效应不可忽略，集中质量方法可能无法正确模拟液体推进剂的运动(如单独助推器的计算)，此时建议采用虚质量法进行计算。

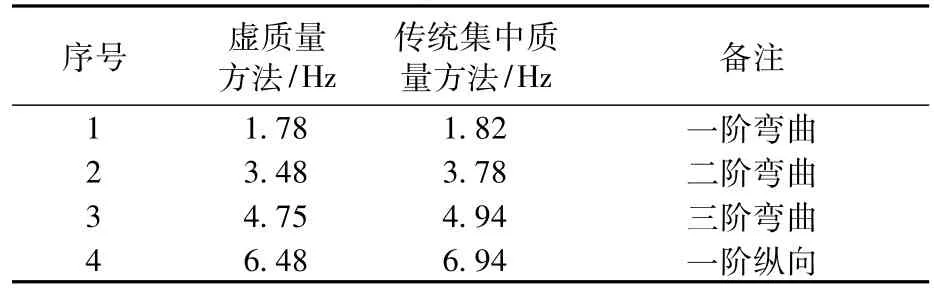
表2 全箭模态计算结果对比Table 2 Modal frequencies of Launch Vehicle

图5 全箭模态振形Fig.5 Modal shapes of launch vehicle

4 结论

本文对动态子结构方法在全箭动特性分析中的应用进行了研究，提出了虚质量法和动态子结构方法相结合的液体推进剂建模方法，并采用不同液体推进剂建模方法对全箭动特性进行了计算分析，得到的主要结论如下:

(1)动态子结构方法可以在保证计算精度的同时，极大的提高了计算效率，比较适合于全箭此类复杂结构的动力学问题研究;

(2)动态子结构与虚质量相结合的液体推进剂建模方法，一方面解决了计算效率问题，另一方面也解决了传统集中质量方法的弊端，可以实现纵、横、扭一体化建模;

(3)对于弯曲模态，虚质量方法和集中质量法均可以很好的描述液体质量的运动状态，因此计算结果一致;对于纵向模态，计算结果与模态形状、液体表现出的质量特性有关。

［1］林宏，罗恒，潘忠文，等.运载火箭动特性有限元模型修正技术研究［J］.载人航天，2011，(6):30-34.

［2］Hou S N.Review of modal synthesis techniques and a new approach［J］.Shock and Vibration Bulletin，1969，40(4):25-39.

［3］MacNeal R H.A hybrid method of component mode synthesis［J］.Computers＆ Structures，1971，1(4):581-601.

［4］Rubin S.Improved component-mode representation for structural dynamic analysis［J］.AIAA Journal，1975，13(8):995-1006.

［5］Craig R，Chang C J.Free-interface methods of substructure coupling for dynamic analysis［J］.AIAA Journal，1976，14(11):1633-1635.

［6］王文亮，杜作润，陈康元.模态综合技术短评和一种新的改进［J］.航空学报，1979，3:32-51.

［7］Hurty W C.Dynamic analysis of structural systems using component modes［J］.AIAA Journal，1965，3(4):678-685.

［8］Suarez L E，Singh M P.Improved fixed interface method for modal synthesis［J］.AIAA Journal，1992，30(12):2952-2958.

［9］Kubomura K.A theory of substructure modal synthesis［J］.Journal of Applied Mechanics，1982，49(4):903-909.

［10］Jezequel L，Seito H D.Component modal synthesis methods based on hybrid models，part i:Theory of hybrid models and modal truncation methods［J］.Journal of Applied Mechanics，1994，61(1):100-108.

［11］邱吉宝，向树红，张正平.计算结构动力学［M］.合肥:中国科学技术大学出版社，2009:346-446.

［12］杨剑，张璞，陈火红.新编MD Nastran有限元实例教程［M］.北京:机械工业出版社，2007:315-335.