基于性能退化模型的空间电子学设备加速寿命试验研究与应用
2014-11-20伏洪勇
伏洪勇,党 炜,李 锴
(1.中国科学院空间应用工程与技术中心,北京100094;2.中国科学院光电研究院,北京100094)
1 引言
空间应用系统主要研制空间有效载荷,其性能要求高,创新性和探索性强,采用新技术、新工艺、新器件、新材料等是必然的选择,在可靠性和寿命上面临极大的挑战。尽管设计人员在设计阶段会考虑许多影响可靠性和寿命的因素,但空间环境因素、产品运控工况复杂,不通过试验验证很难对不确定因素进行准确把握和有效防范。因此,作为空间有效载荷重要组成部分的电子学整机系统,其可靠性和寿命也需要重点关注。
对电子学整机系统的可靠性验证方法国内外研究比较多,有许多比较成熟的方法[1],但对于空间小子样(有时甚至只有1件)产品,工程研制周期短且受经费严重制约,完全采用批量产品的做法,显然难以为航天工程所接受。探索适合空间电子学整机系统加速寿命试验的有效方法是当前亟待解决的问题,基于空间应用系统的实际需求和背景,本文以性能退化模型为基础提出空间电子学整机系统加速寿命试验方法,以评估整机系统在正常工作应力下的性能退化量,为空间电子学整机系统可靠性试验提供一种技术途径。
2 加速寿命试验原理
2.1 加速性判断准则
在进行加速寿命试验时,首先需要判断产品是否具有加速性。加速性就是指在加速试验过程中,受试产品在短时间高应力作用下表现出的特性与产品在长时间低应力作用下表现的特性是一致的。目前最常用的判断产品是否存在加速性的3 个条件为[2]:
1)失效机理的一致性,即在加速应力下和正常使用应力下,产品组成单元的失效机理不发生变化;
2)加速寿命过程中的加速失效具有规律性,即在加速失效过程中,产品寿命与应力之间存在一个确定的函数关系(加速模型),或未知但客观存在的某种关系;
3)失效分布的同一性,即在不同应力水平下产品的寿命服从同一形式的分布,如威布尔分布的形状参数m保持不变,正态分布的标准差σ保持不变。
失效机理的一致性是加速试验的必要条件,但不是充分条件;失效分布的同一性是对加速失效规律性的具体化和定量化。
2.2 常用加速寿命模型及加速系数
物质失效模型比较多,空间产品电子学产品失效热应力是主要的影响因素,空间电子学整机系统常常采用温度应力加速试验进行可靠性余量鉴定和应力筛选。本文结合实际空间工程中的可行性和具体情况,主要介绍以温度应力为主的电子学产品失效机理模型。
1)阿伦尼斯模型及加速系数
1889年,阿伦尼斯(Arrhenius)在研究温度对酸催化蔗糖水解转化反应的基础上总结出:某产品性能退化速率与激活能的指数成反比,与温度倒数的指数成反比。其数学描述为[3]公式(1)。

式(1)中:M—产品某特性值的退化量;t—反应时间(产品寿命);—温度在T时的退化速率,退化速率是时间t的线性函数;k—波尔兹曼常数,为8.617×10-5eV/℃;T—热力学绝对温度;A—常数;Ea—失效机理激活能,以eV为单位,同一类元器件的同一种失效模式为常数。
令M0为产品初始状态性能退化量,经时间t后,产品的性能退化量为M(若退化量达到M就认为产品失效,则t即为产品的寿命),则在时间t内,产品的累积性能退化量如式(2)所示。

对(2)式进一步计算处理,可得如(3)所示等式。

式(3)中,K—性能退化率,其余符号定义与(1)式相同。根据加速系数的定义,可以推导如(4)所示加速系数的表达式。

式(4)中,AF—加速系数;Luse—产品在使用环境下的寿命;Lstress—产品在加速试验环境下的寿命;Kuse—产品在使用环境下的性能退化率;Kstress—产品在加速试验环境下的性能退化率;Tuse—产品在使用环境下的温度;Tstress—产品在加速试验环境下的温度;其余符号与(1)式相同。通过(4)式可知,对于很少出现失效的长寿命产品,可以依据(2)、(3)式的性能退化量相同来计算加速试验的加速系数,进而设计加速试验。
2)Norris-Landzberg模型及加速系数
在1969年,Norris&Landzberg根据 Coffin-Manson模型研究集成电路焊接工艺可靠性问题时给出了其加速模型。Coffin-Manson模型[4]的数学描述如式(5)所示。

式(5)中,Nf—产品至失效的循环数;ΔT—产品的循环温度差;C0—材料依赖常数;n—与材料有关的常数(一般情况下,易碎材料取值3~10,韧性材料取值1.2~2.5;硬金属材料取值1~2)。Coffin-Manson模型主要描述的是在热循环应力下低周疲劳寿命模型,1969年,Norris&Landzberg在该模型基础上研究集成电路焊接工艺可靠性问题时,提出了式(6)所示的焊点工艺加速系数计算方法[5]。

3)Peck模型及加速系数
1986年,D.S.Peck在汇总多稳态实验结果的基础上,在85℃/85%RH条件下研究塑封器件寿命情况的分析基础上,给出了塑封器件的寿命关系式,其数学描述如式(7)所示[6]。

式(7)中,tL—产品寿命;C—标度常数;RH—相对湿度,按%表示;n—经验常数,与封装材料有关,一般取值范围为2~12;其余符号同(1)式定义。
根据加速系统的定义可知,湿热应力加速试验下的加速系数如式(8)所示。
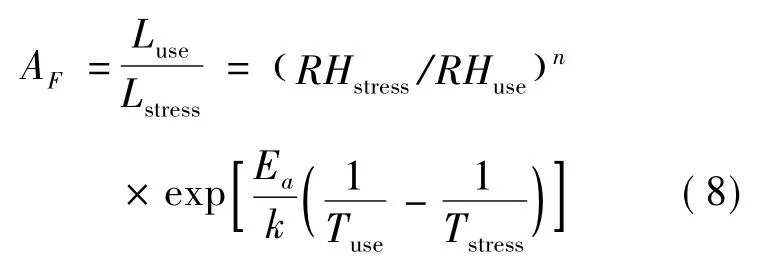
式(8)中,RHuse—使用环境下相对湿度(%);RHstress—加速应力环境下相对湿度(%);其余符号同(2)式和(5)式的定义。通过(8)式可知,Peck模型可以理解为湿度和温度的双应力加速寿命模型,温度应力主要是基于阿伦尼斯(Arrhenius)模型的性能退化模型。
3 电子学整机系统加速寿命试验方法
空间应用系统研究是以科学创新为首要目标,有效载荷是实现科学创新目标的首要手段,其载荷产品的质量和可靠性是科学目标能否实现的关键,因此空间应用系统始终应将产品的质量、可靠性放在重要位置。对于采用了新技术、新工艺、新器件、新材料的创新性载荷,特别是其中的关键单机、组件或关键工艺,将根据工程需要,按照加速寿命试验的基本思路在加大应力情况下加快产品性能退化直至失效,以达到缩短试验时间的目的。以往工程经验和部分文献资料表明:对于空间电子学整机系统设计加速寿命试验主要存在以下两大难点:
1)整机系统因器件、部件、材料种类多,组成复杂,失效模式多,很难建立整机系统在加速应力条件下与正常使用条件下的失效关系模型,很难将加速寿命理论直接应用到整机系统;
2)对于空间长寿命产品,一般在很长的时间内也极少出现失效,因此传统的基于失效数据的加速寿命试验处理方法用于这类产品进行加速寿命试验时会遇到一些困难[3]。
基于空间应用系统有效载荷在进行加速寿命试验时遇到的上述两个问题,本文提出利用“水桶原理”将整机系统加速寿命试验转化为薄弱环节的加速寿命试验,即基于产品的故障模式和失效机理分析,寻找整机系统最薄弱环节,根据最薄弱环节选用合适的性能退化加速模型计算加速因子,来设计加速寿命试验激发整机系统薄弱环节的失效模式,实现可靠性增长和任务满足度评价。整机系统的薄弱环节将是具体的组件、器件、材料或工艺,只要试验施加的应力不太大的情况下(工程上整机不超过鉴定级温度,温度敏感组件不超过其允许最高温度),一般会满足加速性原则;采用性能退化加速模型进行加速试验设计,将不再重点关心产品试验是否失效,而是按在正常使用应力与加速应力下性能退化量等效的原则来设计加速试验。根据这一原理的整机系统加速寿命试验工作流程见图1。
确定整机系统加速寿命试验方案的关键环节为确定加速因子,一般有两种方法:①根据现有加速模型进行分析计算获得;②通过试验确定的模型获得。第一种方法确定的加速因子不是特别准确;第二种方法虽然比较准确,但需要大量的试验样本、时间和经费支持[7]。因此,工程上通常采用第一种方法来获得加速系数,对于恒定温度应力、循环温度应力和湿热应力可以参照本文介绍的计算方法计算获得,但其难点在于激活能的获取。目前,美国国防部可靠性信息分析中心公布了电容器、电阻器、半导体分离器件、微电路、光电器件、继电器、开关、连接器等元器件的激活能[8]。因激活能与器件的材料、工艺或失效模式及失效机理有关,采用这些公布的数据可能会对加速系数的准确性有一定影响,图2给出了激活能(Ea)分别为0.5 eV、0.6 eV和0.7 eV的情况下按阿伦尼斯(Arrhenius)加速模型分析计算的加速系数与温度应力水平的关系。

图1 整机系统加速应力试验工作流程Fig.1 The flow chart of the equipment accelerated test

图2 不同激活能的加速系数Fig.2 Acceleration coefficient for various activation energies
从图2可知,在温度不是特别高和激活能不是特别大的情况下,不同的激活能在相同温度水平下的加速系数是比较接近的。另有研究表明[2],在温度为500 K以下时,对于某种失效机理,激活能是不随温度变化的常数,这也保证了加速寿命试验等效性能退化量的可行性。因此在工程上,只要激活能取的比较合适(最好取厂家或研究人员提供的直接测试数据[9-12]),在试验温度应力不太高的情况(如设备鉴定级温度),根据整机系统的薄弱环节采用本文介绍的加速性能退化模型分析计算加速系数来制定电子学整机系统的加速寿命试验方案是可行的。
4 实例分析
1)某有效载荷电子学整机系统按阿伦尼斯加速模型设计加速应力试验
某有效载荷电子设备需要实现激光通信,在轨需要累计运行3000 h,采用加速应力进行准加速寿命试验,定性验证设备在轨完成任务的能力或实现可靠性增长。
经分析,该设备的薄弱环节为AlGaAs/GaAs激光器组件,不仅失效率高,而且寿命也比较低。对其失效模式和失效机理、任务环境剖面等进行分析后,决定采用恒定热真空加速应力试验,以阿伦尼斯(Arrhenius)加速模型理论为基础(见式(4)),参考国外公布的该类型器件的激活能数据[12],设计了试验方案,确定的试验参数如表1所示。

表1 激光器加速试验方案Table 1 Accelerated tests for lasers
按表1确定的加速试验方案完成了加速试验,用250 h加速应力试验来等效了3000 h长时间试验。通过该试验有效暴露激光器光纤缺陷,改进后重新顺利通过该试验,两次试验的性能测试结果如图3所示,准加速寿命试验实现了产品可靠性增长。
2)某有效载荷电子学整机系统按Norris-Landzberg加速模型设计加速应力试验
某有效载荷电子学设备因采用了多片大规模ICs,在轨按运控要求每天工作4次,需要运行10 000 h,每次工作温度变化范围为20℃,采用加速应力进行准加速寿命试验,定性验证设备在轨完成任务的能力或实现可靠性增长。
经分析,该设备的薄弱环节为ICs焊接工艺,其焊点的热疲劳寿命将决定整机系统的寿命。对其失效模式和失效机理、任务环境剖面等进行分析后,以Norris-Landzberg加速模型理论为基础(见式(6)),参考国外公布的该类焊点的激活能数据[13],设计了试验方案,确定的试验参数如表2所示。
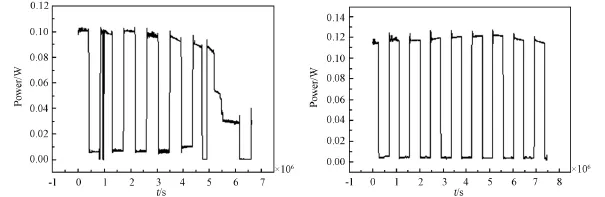
图3 激光器两次试验功率监测情况Fig.3 The result of the lasers power

表2 ICs焊点加速试验方案Table 2 Accelerated tests for ICs solder dots
因此,用200 h加速应力试验来等效10 000 h长时间试验,大大的缩短了试验时间,节省了经费。
3)某有效载荷电子学整机系统按Peck模型设计加速应力试验
某有效载荷电子学设备因其核心器件基本为塑封微电路,在入轨前需要在35℃/60%RH的条件内存放6个月,采用加速应力进行准加速寿命试验,验证设备在存储期间其可靠性是否受环境的影响。
经分析,该设备在存储条件下的薄弱环节为塑封器件,其受潮湿的情况将决定整机系统的寿命。对其失效模式和失效机理等进行分析后,以Peck加速模型理论为基础(见式(7)),参考国外公布的该类型器件的激活能数据[14],设计了试验方案,确定的试验参数如表3所示。

表3 塑封微电路加速试验方案Tab.3 Accelerated tests for the plastic encapsulated microcircuit
因此,用108 h加速应力试验提前验证地面储存条件对单机性能的影响,试验完成后其性能测试结果见图4所示,性能无退化迹象。

图4 产品试验后的性能测试结果Fig.4 The result of the equipment performance after testing
5 结论
空间应用系统有效载荷基本都为创新性有效载荷,国内无现成经验可借鉴,对于采用新技术、新工艺等新手段的电子学整机系统开展专项的可靠性验证或增长试验是必要的,但需要工程可接受,采用加速寿命试验是一种比较好的解决措施。目前,国内外比较成熟的加速寿命试验方法都是基于失效数据的,而空间用设备寿命长、可靠性高、很少出现失效,本文提出针对空间应用的电子学整机系统薄弱环节按性能退化模型设计加速寿命试验是一种比较好的解决方案,当然,该方法对于其它电子学产品也可借鉴使用。但在实际工程中应用时,需要注意以下问题:
1)本文介绍的加速模型主要为产品特征性能参数在正常应力和加速应力下退化量相同而导出的加速系数,不需要产品在不同应力下的寿命数据;
2)整机系统比较复杂,当某薄弱环节在复杂的环境条件下不具有加速性时,不能通过本文介绍的方法去推导整机系统的性能退化历时时间;
3)采用分析计算的方法确定加速系数时,需要考虑激活能等参数的不确定性,合理进行取舍,确保试验充分有效;
4)在实际的工程应用中,应对任务剖面要求的任务时间留有足够的余量,确保试验结果的可信性。
[1]何国伟,戴慈庄.可靠性试验技术[M].北京:国防工业出版社,1995:3-10
[2]张苹苹.航空产品加速寿命试验研究及应用[J].北京航空航天大学学报,1995,21(4):124-129.
[3]林震,姜同敏,程永生,等.阿伦尼斯模型研究[J].电子产品可靠性与环境试验,2006,23(6):12-14.
[4]Ron Weglinski.Highly accelerated stress screening for aircooled switching power supplies[EB/OL].http://www.tdipower.com/pdf/white_paper/hass.pdf.
[5]Norris K C,Landzberg A H.Reliability of controlled collapse interconnections[J].IBM Journal of Research and Development,1969,13(3):266-271.
[6]元器件失效物理模型[EB/OL].http://www.faprl.buaa.edu.cn/ref/day.
[7]Mike Silverman著.高加速寿命试验(HALT)和加速寿命试验(ALT)——两种卓越的可靠性试验技术[M].于晓伟,曾天翔,译,[EB/OL].Mike Silverman著.高加速寿命试验(HALT)和加速寿命试验(ALT)——两种卓越的可靠性试验技术[EB/OL].于晓伟,曾天翔,译.http://www.cetin.net.cn/storage/cetin2/QRMS/ztzsz154.pdf.
[8]Denson W.Handbook of 217Plus Reliability Prediction Models[S].RIAC,2006.
[9]Edward Wyrwas.Performance and reliability of integrated circuits within computing systems[DB/OL].http://www.eetimes.comv.
[10]Blish R,Huber S,Durrant N.Use condition based reliability evaluation of new semiconductor technologies[J/OL].http://www.sematech.org/docubase/document/3810axfr.pdfv.
[11]Michael Osterman.Effect of temperature cycling parameters(dwell and mean temperature)on the durability of pb-free solders[DB/OL].http://calce.umd.edu/lead-free/calceimapsi010.pdfv.
[12]Ott M.Capabilities and reliability of LEDs and laser diodes[R].NASA Goddard Space Flight Center,1997.
[13]Danto Y,Deletage J Y,Verdier F,et al.Evolution of reliability assessment in PCB assemblies[J].Proc XVIth SBMicro,Pirenopolis(Brazil),2001:51-9.
[14]SSP 41172,Qualification and Acceptance Enviromental Test Requirements[S].NASA,2003.
