图的拉普拉斯谱半径对应的特征向量性质及其应用

汪秋分，宋海洲

（华侨大学 数学科学学院，福建 泉州362021）

设G是一个简单的连通图［1］，G＝（V，E）.其顶点集V＝｛v1，v2，…，vn｝，边集E＝｛e1，e2，…，em｝.记顶点vi的度为di，i＝1，2，…，n.记D（G）＝diag｛d1，d2，…，dn｝和A（G）分别为G的度对角矩阵和邻接矩阵［2］，则L（G）＝D（G）－A（G）为G的拉普拉斯矩阵［3］.显然，L（G）是半正定、对称和奇异的.称L（G）的特征值为G的拉普拉斯特征值，记为μ（G）＝μ1（G）≥μ2（G）≥…≥μn（G）＝0.特别的，称μ（G）为G的拉普拉斯谱半径［4］.树是含n个顶点，n－1条边的简单连通图.图G中所有的度为1的顶点称为图G的悬挂点［5］.记NG（v）表示图G中与v相邻接的顶点集，dv表示图G中顶点v的度.有关图的拉普拉斯谱半径的结果有很多，如郭继明［6］的加边或嫁接边对图的拉普拉斯谱半径的影响，袁西英等［7］的树的运算及其Laplace谱，郭继明［8］的树的拉普拉斯谱半径，谭尚旺［9］的关于树的拉普拉斯谱半径，张晓东［10］的给定度序列的树的拉普拉斯谱半径，等等.本文给出了图的拉普拉斯谱半径对应的特征向量的性质及应用，并得到了一些有关图的移接变形对拉普拉斯谱半径影响的结果.

1 相关定义与性质

1.1 图的拉普拉斯谱半径对应的特征向量的定义

介绍其定义之前，先证明一个定理.

定理1设G＝（V，E）是一个简单的连通图，且｜V｜＝n.记L（G）为图G的拉普拉斯矩阵，有时也简记为L，μ（G）为图G的拉普拉斯谱半径.则对于向量x∈Rn×1，有

1）μ（G）＝为L（G）的n个特征值；

2）μ（G）＝

3）若‖x‖＝1，且x′L（G）x＝μ（G），则L（G）x＝μ（G）x.

证明 1）由拉普拉斯谱半径的定义容易证明.

2）由于L（G）是一个实对称矩阵，因此，存在一个正交矩阵P，使得P－1LP＝diag（μ1，μ2，…，μn），其中，μ1，μ2，…，μn为L（G）的n个实特征值.

令diag（μ1，μ2，…，μn）＝D，P＝（P1，P2，…，Pn），x＝Py，则有

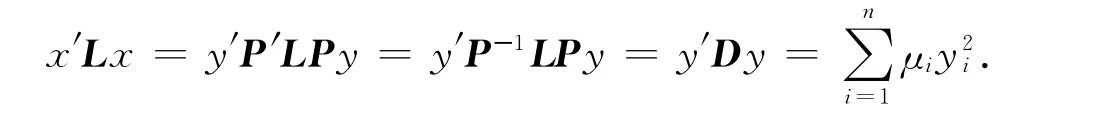
又由于P是正交矩阵，并且有x＝Py.因此，当‖x‖＝1时，有‖y‖＝1.不失一般性，可假设μ1≤μ2≤…≤μn.因而有

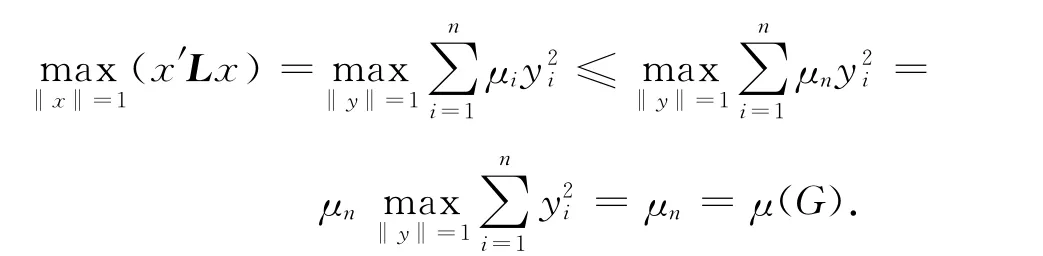
令y＊＝en＝（0，0，…，0，1）′n×1，记x＊＝Py＊＝Pn，则上面不等式等号成立.因此有

3）设μ1，μ2，…，μn为L（G）的n个特征值，P，D，y的含义同2）.不失一般性，可设μ1≤μ2≤…≤μn.则由1）可知μ（G）＝μn.又由于x′L（G）x＝μ（G），因此x′L（G）x＝y′Dy＝μ（G）＝μn.即有y′Dy＝μn.

易知L（G）是一个实对称半正定矩阵，且μ1＝0，μn＞0.不妨假设实数s（1≤s≤n）是满足μs＜μs＋1且μs＋1＝μn的最大自然数.所以y＝（01×s，Z）1×n，其中，实向量Z∈R1×（n－s）且‖Z‖＝1.记Z＝（ys＋1，ys＋2，…，yn），则有可知x是L（G）的对应于的特征向量，因此有L（G）x＝μ（G）x.

下面给出图的拉普拉斯谱半径对应的特征向量的定义.

定义1设G＝（V，E）是一个简单的连通图.若向量x∈Rn×1满足‖x‖＝1，且x′L（G）x＝μ（G），则称x为图G的一个规范拉普拉斯谱向量.

1.2 图的拉普拉斯谱半径对应的特征向量的性质

下面给出有关图的拉普拉斯谱半径对应的特征向量的一些性质.

定理2设T是一棵树，其顶点集V＝｛v1，v2，…，vn｝.记L（T）为T的拉普拉斯矩阵，μ（T）为T的拉普拉斯谱半径.若x为T的一个规范拉普拉斯谱向量，且x＝（x1，x2，…，xn）′.则有：1）x为实向量；2）｜x｜＞0，其中，｜x｜＝（｜x1｜，｜x2｜，…，｜xn｜）′.

证明 1）由题意可知：L（T）是实对称矩阵.又μ（T）也为实数，因此，x为实向量.

2）反证法.假设｜x｜＞0不成立，必然存在一个顶点集H＝｛vj1，vj2，…，vjt｝，使xjl＝0（l＝1，2，…，t），其中，1≤t≤n，1≤j≤n，xj为顶点vj对应于一个规范拉普拉斯谱向量的分量.

又由于x为T的一个规范拉普拉斯谱向量，因而有‖x‖＝1.所以x≠0，且存在顶点v∈V（T）使得xv＝0，及顶点u∈NT（v）使得xu≠0.

设T是以顶点v为根节点的根树，记NT（v）＝｛w1，w2，…，ws｝.另记Ti为由wi及wi的所有子孙组成的子树，i＝1，2，…，s.令yv＝xv＝0，ywi＝｜xwi｜，当xwi≥0时，有yj＝xj（vj∈Ti），当xwi＜0时，有yj＝－xj（vj∈Ti），i＝1，2，…，s.

因此，有ywi≥0，i＝1，2，…，s，‖y‖＝1且y′L（T）y＝x′L（T）x＝μ（T）.由定义1可知，y是T的一个规范拉普拉斯谱向量.根据定理1可得L（T）y＝μ（T）y.又已知L（T）＝D（T）－A（T），则（D（T）－A（T））y＝μ（T）y.故（（D（T）－μ（T）I）y）v＝（A（T）y）v.因此可得

然而ywi≥0，且存在i0＝∈｛1，2，…，s｝，使得wi0＝u满足yu＞0.因而，从而导致矛盾，原命题成立.

定理3设T是一棵树，v是T的一个顶点，v1，v2，…，vs是与v相邻的悬挂点.若x＝（x1，x2，…，xn）′为T的一个规范拉普拉斯谱向量，这里xi对应于顶点vi，1≤i≤n，则xvj＝xvi，1≤i＜j≤s.

证明 由于x＝（x1，x2，…，xn）′为T的一个规范拉普拉斯谱向量，由定理1及定义1可得

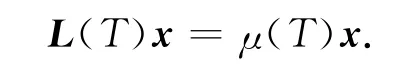
又已知L（T）＝D（T）－A（T），则有（D（T）－A（T））x＝μ（T）x，所以可得（（D（T）－μ（T）I）x）vi＝（A（T）x）vi＝xv，i＝1，2，…，s.从而有（1－μ（T））xv1＝xv，（1－μ（T））xv2＝xv，…，（1－μ（T））xvs＝xv.因此xvj＝xvi（1≤i＜j≤s）.

定理4设T＝（V，E）是一棵树，其顶点集V（T）＝｛v1，v2，…，vn｝，边集记为E（T）.若x＝（x1，x2，…，xn）′为T的一个规范拉普拉斯谱向量，xi对应于顶点vi，1≤i≤n.则有：1）对于任意边uv∈E（T），有

证明 1）由于x为T的一个规范拉普拉斯谱向量，由定义1可得

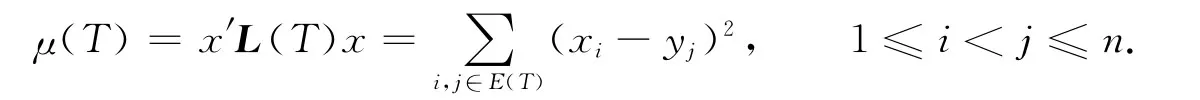
对任意uv∈E（T），由定理2可得｜xu｜＞0且｜xv｜＞0，所以有xuxv≠0.

设存在边uv∈E（T）使得xuxv＞0.设T是以r为根节点的根树，可设顶点u是顶点v的父节点（图1）.设T1＝（V1，E1）是由v及v的所有子孙组成的k层子树（图2）.不失一般性，假设xu＞0，故xv＞0.

取y＝（y1，y2，…，yn）′，令yi＝xi（i∉V1），yw1＝－｜xw1｜（w1是T1的第1层上的顶点，即w1＝v），yw2＝（－1）2｜xw2｜（任意w2是T1的第2层上的顶点），…，ywk＝（－1）k｜xwk｜（任意wk是T1的第k层上的顶点）.则有‖y‖＝‖x‖＝1，且有

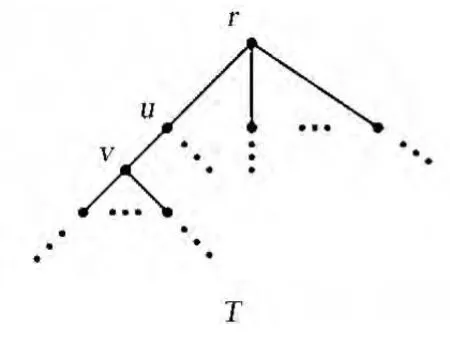
图1 顶点u是顶点 v的父节点 Fig.1 Vertex uis the father vertex of vertex v

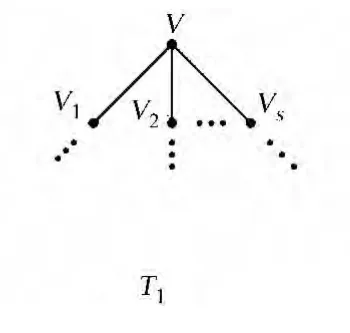
图2 v及v的所有子孙 组成的k层子树Fig.2 Subtree with klevels obtained fromv and v′s descendants

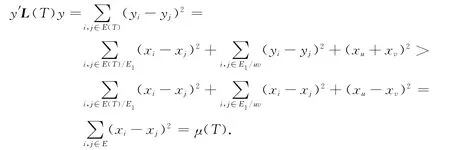
因此，存在一个单位向量y＝（y1，y2，…，yn）′，使μ（T）＜y′L（T）y.这与定理1矛盾，故有xuxv＜0.

2）由于x为T的一个规范拉普拉斯谱向量，因而有（D（T）－A（T））x＝μ（T）x.因此（dvi－所 以 有从 而，所以

2 图的拉普拉斯谱半径对应的特征向量的应用

2.1 加边对图的拉普拉斯谱半径的影响

定理5设u，v是树T的两个顶点.记顶点u，v之间的距离为d（u，v）＝k，其中，k为奇数且k≥3.若G是由T添加新边设uv后所得到的图，则有μ（G）＞μ（T）.

证明 设x＝（x1，x2，…，xn）′为T的一个规范拉普拉斯谱向量，xi对应于顶点vi，1≤i≤n.由于k为奇数且k≥3，由前面定理4可得：xuxv＜0.记T与G的边集分别为E（T）和E（G），因此有

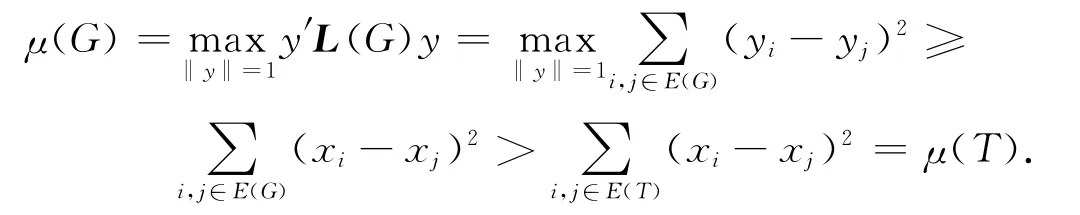
即μ（G）＞μ（T）.

2.2 嫁接对图的拉普拉斯谱半径的影响

定理6设u，v是树T的两个顶点，T＝（V（T），E（T）），且有NT（v）／（NT（u）∪｛u｝）＝｛v1，v2，…，vs｝，1≤s≤dv，设x＝（x1，x2，…，xn）′为T的一个规范拉普拉斯谱向量，xi对应于顶点vi，1≤i≤n，T＊是由T删除边vvi，添加边uvi后所得到的树（1≤i≤s）（图3）.若｜xu｜≥｜xv｜，则μ（T）＜μ（T＊）.

证明 对于树T，设T＝（V，E）形成一根树，且顶点v是v1，v2，…，vs的父节点.令T1是由顶点v，v1，v2，…，vs及v1，v2，…，vs的所有子孙组成的子树，T1＝（V1，E1）.类似的，对于树T＊，设T＊＝（V＊，E＊）形成一根树，u为其根节点，并且顶点u是v1，v2，…，vs的父节点.令T＊1是由顶点u，v1，v2，…，vs及v1，v2，…，vs的所有子孙组成的子树，且T＊1的层次（高度加1）为k.记E′1＝E1／｛vv1，vv2，…，vvs｝.

令yi＝xi（vi∈V／V（T1）），yv＝xv，yw1＝－sgn（xu）｜xw1｜（任意w1是T＊1的第2层上的顶点），yw2＝（－1）2sgn（xu）｜xw2｜（任意w2是T＊1的第3层上的顶点），…，ywk－1＝（－1）k－1sgn（xu）｜xwk－1｜（任意wk－1是T＊1的第k层上的顶点）.则可得‖y‖＝1，且

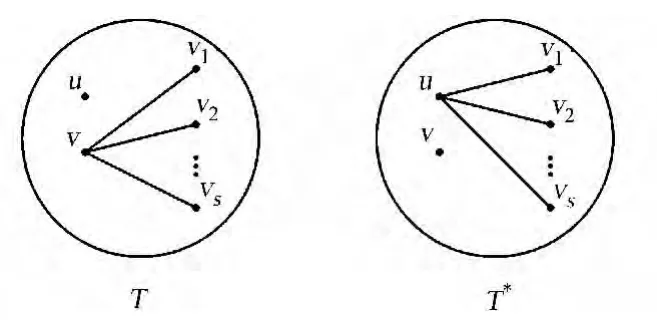
图3 树T和树T＊Fig.3 Tree Tand T＊

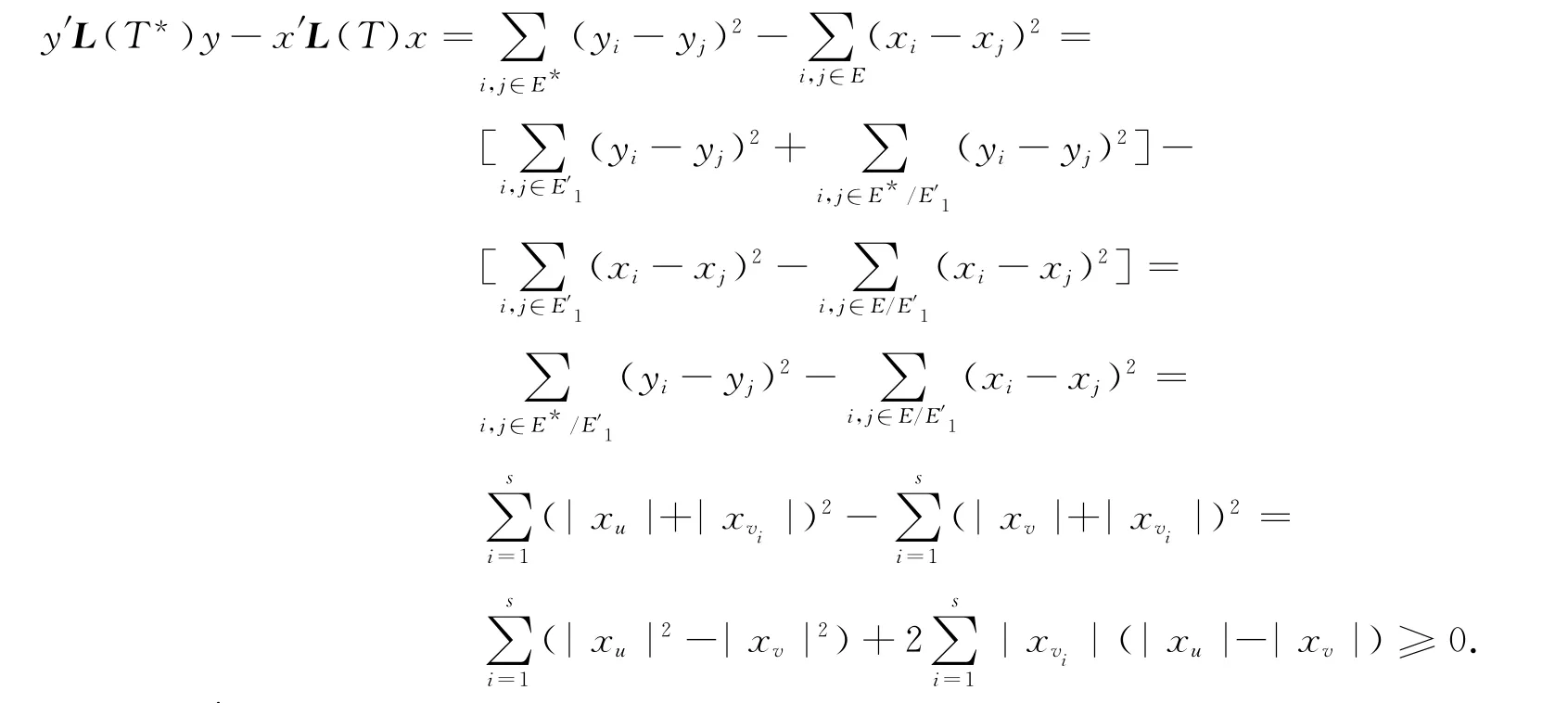
即有y′L（T＊）y≥x′L（T）x.因此

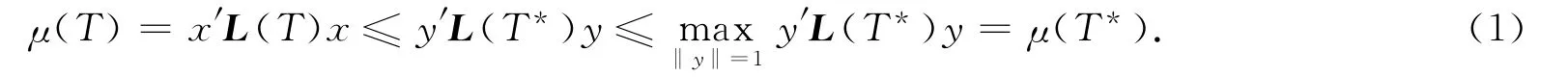
故有μ（T）≤μ（T＊）.

若μ（T）＝μ（T＊），则式（1）中等号成立，故有μ（T）＝y′L（T＊）y＝μ（T＊）.因而，由定理1可以得L（T＊）y＝μ（T＊）y.又L（T＊）＝D（T＊）－A（T＊），所以

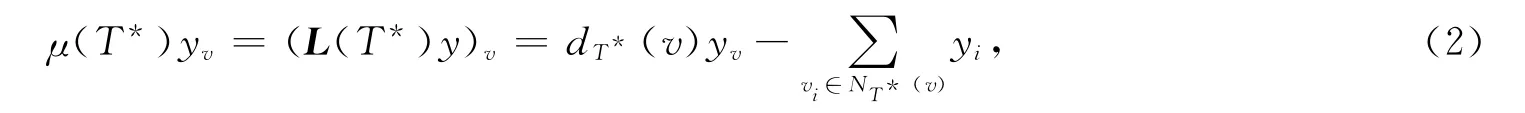
式（2）中：dT＊（v）为顶点v在树T＊中的度.

又L（T）x＝μ（T）x，类似的有

由式（2）～（3）可得

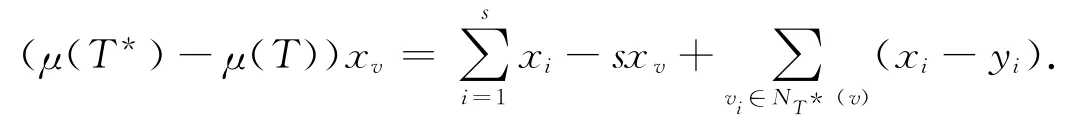
不失一般性，设xv＞0.

若xu＞0，由定理4可得因而有μ（T）＞μ（T＊），这与假设矛盾.

若xu＜0，由定理4可得有μ（T）＞μ（T＊），这也与假设矛盾.

综上所述，若｜xu｜≥｜xv｜，则μ（T）＜μ（T＊）.

推论1设T＊是如定理6所定义的树，若y＝（y1，y2，…，yn）′为T＊的一个规范拉普拉斯谱向量，yi对应于顶点vi，1≤i≤n，则｜yu｜＞｜yv｜.

证明 反证法.若｜yu｜≤｜yv｜，由定理6可得μ（T）＞μ（T＊）.这与定理6结论矛盾，顾原命题成立.

推论2设G＝（V，E）为含n个顶点的树，r，s，t是G的三个不同的顶点，且rs∈E（G），rt∉E（G）.设G＊是由G删除边rs添加边rt后所得到的树.设x＝（x1，x2，…，xn）′为G的一个规范拉普拉斯谱向量，xi对应于顶点vi，1≤i≤n；x＊＝（x＊1，x＊2，…，x＊n）′为G＊的一个规范拉普拉斯谱向量，x＊i对应于顶点v＊i，1≤i≤n.若｜xt｜≥｜xs｜，则｜x＊t｜＞｜x＊s｜.

证明 显然，由题意可知，G是由G＊删除边rt添加边rs后所得到的树.假设｜x＊t｜≤｜x＊s｜，由定理6可得μ（G）＞μ（G＊）.又｜xt｜≥｜xs｜，由定理6得μ（G）＜μ（G＊）.这样导致矛盾，因此原命题成立.

［1］汪秋分，宋海洲.图谱理论中一些定理的新证明［J］.华侨大学学报：自然科学版，2012，33（4）：477－480.

［2］刘亚国.图论中邻接矩阵的应用［J］.忻州师范学院学报，2008，24（4）：18－19.

［3］谭尚旺，张德龙.一定条件下图的拉普拉斯矩阵的谱半径［J］.广西科学，2008，15（4）：352－356.

［4］LI Jian－xi，SHIU Wai－chee，CHAN Wai－hong.The Laplacian spectral radius of some graphs［J］.Linear Algebra Appl，2009，431（1）：99－103.

［5］WU Bao－feng，XIAO En－li，HONG Yuan.The spectral radius of trees onkpendant vertices［J］.Linear Algebra Appl，2005，395（15）：343－349.

［6］GUO Ji－ming.The effect on the Laplacian spectral radius of a graph by adding or grafting edges［J］.Linear Algebra Appl，2006，413（1）：59－71.

［7］袁西英，吴宝丰，肖恩利.树的运算及其Laplace谱［J］.华东师范大学学报：自然科学版，2004，50（2）：13－18.

［8］GUO Ji－ming.On the Laplacian spectral radius of a tree［J］.Linear Algebra Appl，2003，368（15）：379－385.

［9］TAN Shang－wang.On the Laplacian spectral radius of trees［J］.Chinese Quarterly Journal of Mathematics，2010，25（4）：615－625.

［10］ZHANG Xiao－dong.The Laplacian spectral radii of trees with degree sequences［J］.Discrete Mathematics，2008，308（15）：3143－3150.