干扰泄漏最小的多小区MIMO干扰对齐算法

袁继昌，赵睿

（华侨大学 信息科学与工程学院，福建 厦门361021）

由于无线通信系统采用了同频组网的方式，使得小区边缘的用户遭受到来自非服务小区基站发送的同频干扰，严重地制约系统性能.因此，多小区多输入多输出（MIMO）系统中的干扰抑制技术成为现代无线通信领域中的一个研究热点.协作多点传输（CoMP）技术，可以有效地消除小区间干扰［1－2］，而干扰对齐技术则是作为CoMP技术中的关键技术之一［3－10］.文献［3］研究了k对单天线干扰对齐系统模型，当信道是时变时，每个用户可获得1／2的自由度，而与用户数无关.文献［4］利用信道互异性提出一种分布式迭代干扰对齐算法.文献［5］提出了一种正规化迫零干扰对齐（RZF－IA）算法，该算法具有消耗的资源少，迭代速度快的优点.文献［6］通过在时域或频域上对干扰信道对角化可获得更高的分集增益.文献［7－8］分别从改善接收端信号质量和提升系统速率的角度，对文献［3］中的随机选取预编码向量进行了改进.但是这些方案均未考虑基站2，3先获取预编码时对系统性能的影响.基于此，本文提出了一种基于系统总干扰泄漏最小的预编码组的选择算法.

1 系统模型

考虑k小区MIMO下行多用户系统，每个小区仅服务一个用户，用户k（k＝1，2，…，K）除了接收到服务小区基站发送的期望信号，还会接收到来自非服务小区基站发送的干扰信号，基站和用户均配置M（M为偶数）根天线，3用户干扰对齐系统模型，如图1所示.

用户k接收到的信号可表示为

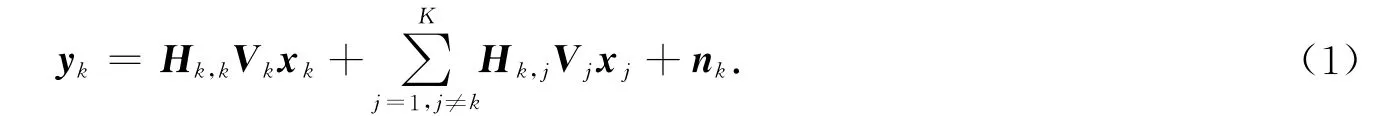
式（1）中：Hk，j为基站j到用户k的信道矩阵，假设所有的用户经历平坦瑞利衰落，Hk，j中的每一个元素均服从独立同分布零均值单位方差的复高斯随机分布（AWGN），即CN（0，1）；Vj为基站j发送的预编码矩阵；xj为基站j发送的信号矢量，并满足功率约束条件

其中Pj表示基站j发送的功率；nk为用户k的加性高斯白噪声矢量，其分布满足nk～CN（0，σ2I）.

定义接收端的干扰抑制滤波器为Uk，则用户k对接收信号进行滤波后可得到

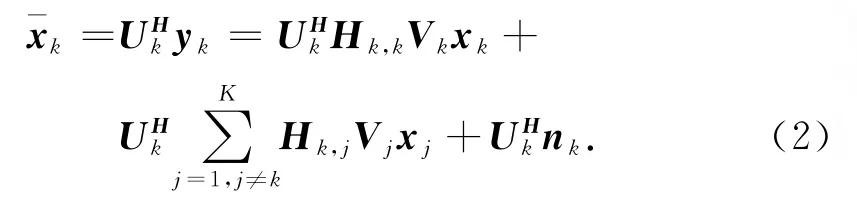
式（2）中：Uk可通过文献［8］中算法求得.

因此，期望信号经过满秩信道矩阵

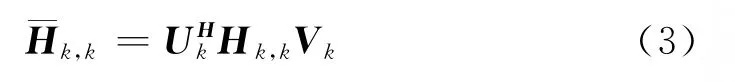
的同时，可将干扰完全消除.式（2）可等效为

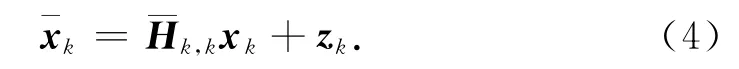
式（4）中：zk～CN（0，σ2Idk）是用户k的等效dk×1的AWGN向量；dk为用户k获得空间自由度.

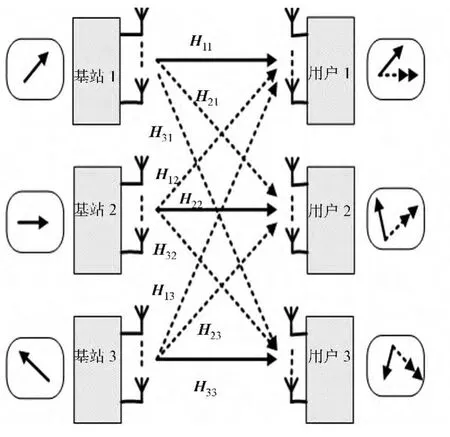
图1 干扰对齐系统模型Fig.1 System model of interference alignment

因此，用户k获得的速率为

系统获得的和速率为

2 经典干扰对齐方案

在3用户干扰对齐模型（图1）中，假设发射端和接收端均配置M根天线，M为偶数.发射端预编码矩阵满足的条件［3］为

式（7）中：span（X）是由矩阵X的列向量张成的空间.

式（7）的限制条件进一步加强为

经过简单的矩阵变换，式（8）的等效变换可表示为

式（9）中：E1＝（H3，1）－1H3，2（H1，2）－1H1，3（H2，3）－1H2，1为变换矩阵.

由式（9）可知：V1为E1的特征矢量组成的预编码.

由于系统获得的总的发射自由度为3M／2［3］，因此可独立地发送M／2个独立的数据流，xk和Vk分别为（M／2）×1的矢量和M×（M／2）的矩阵，所以V1可表示为

式（10）中：e1，e2，…，eM／2为E1的任意M／2个特征向量.

根据式（9）可求得V2和V3.

3 干扰泄漏最小的预编码组选择算法

3.1 经典干扰对齐优化算法

经典干扰对齐方案并未对本地用户经历的期望信道做预处理.文献［7］提出了一种基于特征子信道的干扰对齐预编码矩阵优化方案，然而没有考虑到预编码矩阵与干扰信道的奇异值分解右奇异矩阵的关系.文献［8］提出了一种协作干扰对齐优化算法，对接收端干扰抑制矩阵进行优化，进一步提升了系统的性能.

3.2 预编码组选择算法

从式（9）可以看出：基站j（j≠1）的预编码设计与基站1获得的预编码有密切的关系，即第一个获得预编码的基站，直接影响到其他两个基站预编码的设计.但文献［3，7，8］都未对基站2，3分别先获得预编码时对整体系统性能的影响进行分析.针对这一不足之处，提出了一种基于系统总干扰泄漏最小预编码组的选择算法.将式（9）重新改写为

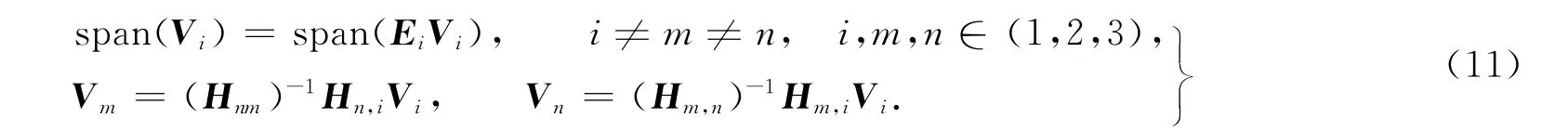
式（11）中：Ei＝H－1n，iHn，mH－1i，mHi，nH－1m，nHm，i.

具体的算法有如下6个步骤.

1）计算Ei＝H－1n，iHn，mH－1i，mHi，nH－1m，nHm，i，i≠m≠n，i，m，n∈（1，2，3）.

2）计算Vi＝vm／2（Ei）.

3）依据公式（5）求Vm和Vn.

4）计算系统的总干扰泄漏.

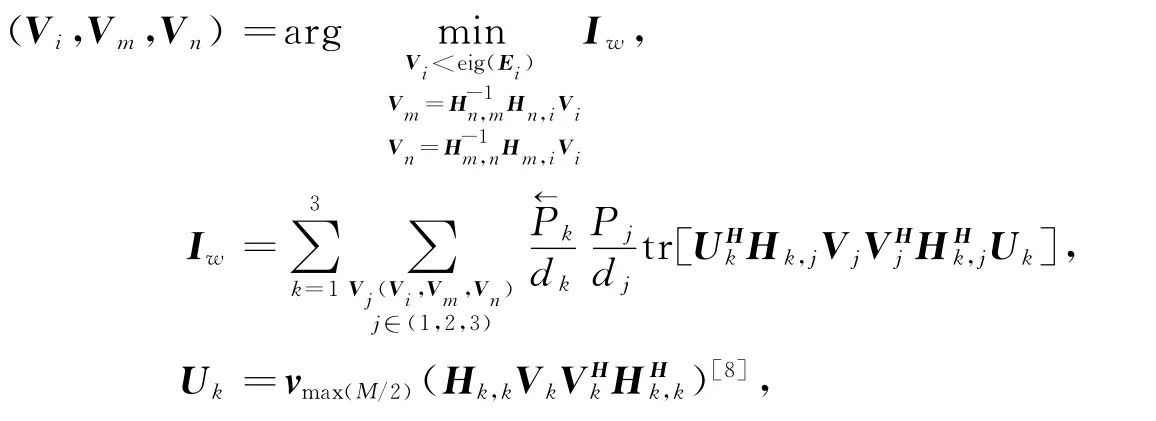
则最优的预编码组（Vi，Vm，Vn）所对应的Ei为需要选择的最优E.

5）根据选择出的最优E重新计算步骤2）［8］，即

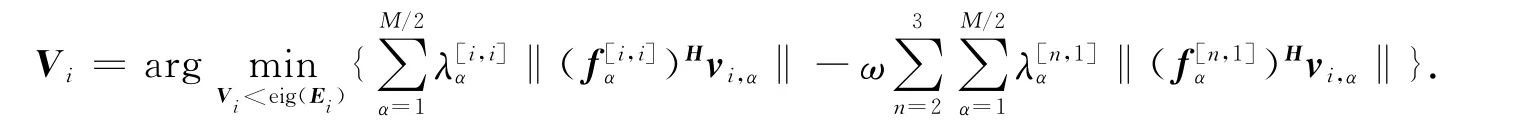
其中：fα为Hi，i的特征值λα对应的右奇异向量第α列；vi，α为Vi中对应的第α列；ω为权重因子，它表示干扰对齐预编码矩阵与干扰信道的弦距之和占预编码矩阵与期望信号弦距之和的比重［9］.

6）在图1系统模型下，3个基站联合预编码设计可表示为

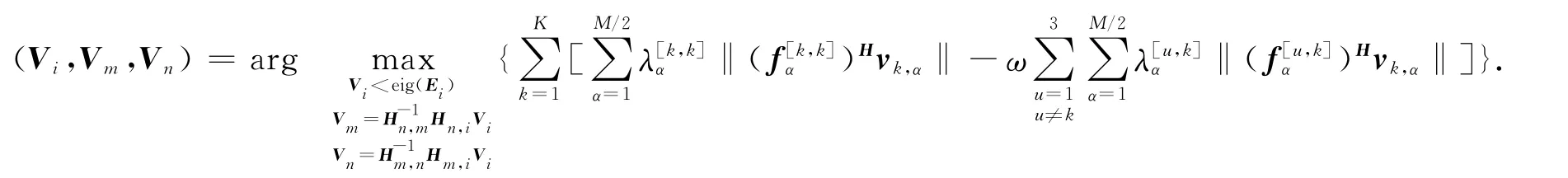
3.3 计算复杂度分析

1）由式（9）可知，经典干扰对齐方案的复杂度为每个小区基站需要浮点运算次数：700M3－1M2＋3M.

2）文献［7］中的特征子信道干扰对齐方案的复杂度为每个小区基站需要浮点运算次数：700M3－11M2＋126M3＋3（M／2）（7M－1）M／2M＝826M3－11M2＋3M＋

3）文献［8］中的协作干扰对齐方案的计算复杂度为每个小区基站需要浮点运算次数：700M3－11M2＋3M＋378M3＋9（M／2）（7M－1）M／2M＝1 078M3－11M2＋3M＋

4）文中系统总干扰泄漏最小预编码组的选择算法的计算复杂度为每小区基站需要浮点运算次数：3（700M3－11M2＋3M＋7M3）＋3（M／2）（7M－1）M／2M＝826M3－11M2＋3M＋1 078M3－11M2＋3M＋

取最大值M＝4，经典干扰对齐算法的复杂度为44 636次浮点运算；文献［7］中算法为54 644次浮点运算；文献［8］中算法为74 660次浮点运算；文中的算法计算复杂度略有增加，复杂度为209 912次浮点运算.

3.4 新算法在统计信道状态信息下的性能

以上方案大都假设基站端已知所有用户的完全信道状态信息，或者通过有限反馈技术获取用户的信道状态信息（CSI）.但是，在实际系统中很难获取完全信道状态信息（Full－CSI）.对于容量有限的反馈回程链路，基站间大量的信息交互无疑会增加其负载，而且有限反馈又不可避免地带来发送端获取CSI失真.这是由于统计信道状态信息（SCSI）在一段时间内的变化相对缓慢，基站端的SCSI很容易通过长期反馈或上下行链路的互异性获取.

4 仿真结果与分析

利用Matlab仿真工具，首先分析所提出的系统总干扰泄漏最小的预编码组选择算法的速率性能，并与文献［3，7，8］中的算法相比较.仿真环境为小区数和用户数K＝3，基站和用户均配置M＝4根天线.不同干扰对齐算法的和速率随SNR变化曲线，如图2所示.由图2可知：提出的算法在和速率性能上比其他3种算法都有较大的改进.这是由于对系统发射端获取的第一个预编码矩阵进行了优化选择，而其他发射端预编码矩阵的设计又依赖于这个预编码矩阵.

与单纯的使用式（9）获取的预编码矩阵组相比，系统获取这样的一组预编码矩阵可使系统的总干扰泄漏最小，因此其和速率性能自然是最优的.仿真环境与图1相同，信道相关系数（γ）如图3所示.从图3中可以看出：文中提出的算法在相关信道下有更强的适应性.

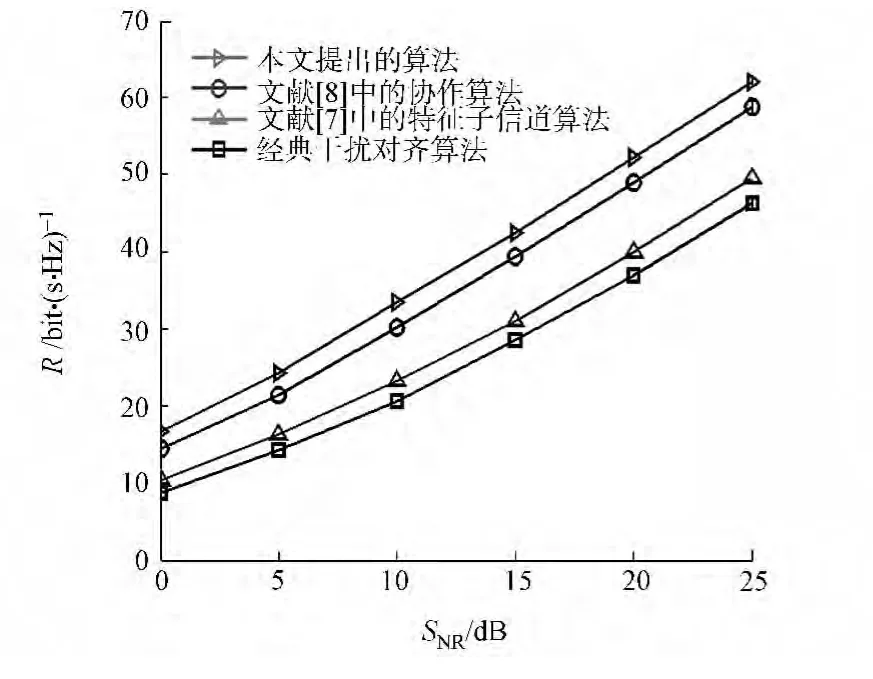
图2 不同干扰对齐算法的 和速率随SNR变化的曲线 Fig.2 Sum－rate curves of different interference interference alignment alignment algorithms

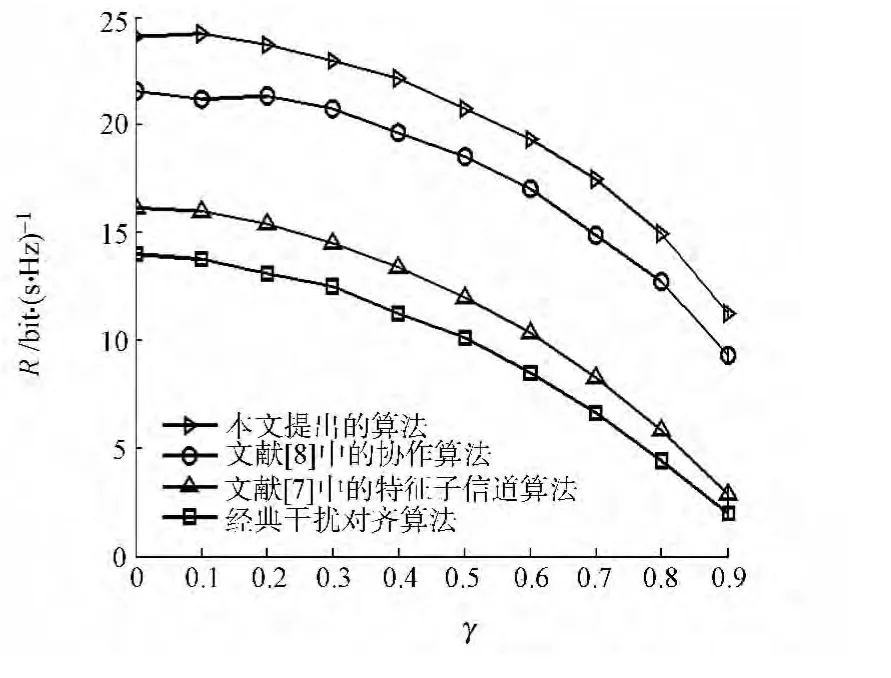
图3 不同干扰对齐算法的和速率随相关系数变化的曲线Fig.3 Sum－rate curves of different algorithms under different correlation factors

5 结论

研究了3小区MIMO通信系统中经典干扰对齐算法的优化算法.通过最小化干扰泄漏准则，遍历系统中所有的预编码矩阵组.并从中选出一组最优的预编码矩阵组，仿真结果表明：文中提出的发射机预编码矩阵组的选择算法可以有效地提升系统的和速率性能.

比较了现有干扰对齐算法和提出的算法在统计信道状态信息下的性能，结果表明：文中提出的算法在相关信道下同样可以获得很好的和速率性能.

［1］PATRICK M，GERHARD F.Uplink CoMP under a constrained backhaul and imperfect channel knowledge［J］.IEEE Transactions on Wireless Communications，2011，10（6）：1730－1742.

［2］KLICHUN W，CHUJUNG Y.3－cell network MIMO architectures with sectorization and fractional frequency reuse［J］.IEEE Jouranal on Selected Areas in Communications，2011，29（6）：1185－1199.

［3］CADAMBE V R，JAFAR S A.Interference alignment and degrees of freedom of the K－user interference channel［J］.IEEE Transactions on Information Theory，2008，54（8）：3425－3441.

［4］GOMADAM K，CADAMBE V R，JAFAR S A.A distributed numerical approach to interference alignment and applications to wireless interference networks［J］.IEEE Transactions on Information Theory，2011，57（6）：3309－3322.

［5］SUH C，HO M，TSE D.Downlink interference alignment［J］.IEEE Transactions on Communications，2011，59（9）：2616－2626.

［6］SONG S H，CHEN X，LETAIEF K B.Achievable diversity gain of k－user interference channel［J］.IEEE International Conference on Communications，2012，28（9）：4197－4201.

［7］王存祥，邱玲.协作多点传输中一种基于特征子信道的干扰对齐预编码矩阵优化算法［J］.信号处理，2011，27（3）：395－399.

［8］徐冰，谢显中，马彬，等.MIMO干扰信道下的协作干扰对齐优化算法［J］.信号处理，2012，28（2）：220－225.

［9］KUMAR K R，XUE F.An iterative algorithm for joint signal and interference alignment［J］.IEEE International Symposium Information Theory Proceedings，2010，55（7）：2293－2297.

［10］VANZELST A，SCHMIDT J S H.A single coefficient spatial correlation model for multiple－input multiple－output（MIMO）radio channels［C］∥Pro URSI General Assembly.Maastricht：Netherlands，2002：1－4.