遥感图像分类的多核SVDD算法
2014-11-19陈赛英何建农
陈赛英,何建农
(福州大学 数学与计算机科学学院,福建 福州350108)
遥感图像分类是模式识别技术在遥感技术领域的一个具体应用,是对遥感图像信息进行属性的分类,达到识别图像信息所对应的实际地物,最后提取所需地物信息的目的.支持向量域描述(SVDD)算法具有复杂程度低、扩充性强,以及对训练样本数据规模上要求不高等优点,已经广泛应用于故障诊断、异常检测、语音识别等多种领域[1-4].SVDD算法的核心部分是核函数的选择,传统SVDD算法通常是以径向基核函数为核函数,但径向基核函数存在计算量大、泛化性能较弱等缺点[5].基于此,本文分别将K型核函数和指数径向基核函数与径向基核函数组合成多核函数,构造SVDD的改进算法,并应用于遥感图像分类.
1 SVDD模型的原理[6]
SVDD算法是基于贝叶斯最优决策理论的,其基本思想是通过非线性变换将数据点映射到高维特征空间,然后找到包含大部分映射到特征空间数据点的最小超球体(图1).令{xi}⊂X是数据空间X⊂Rn的一个给定训练数据集,用一个非线性变换Φ把X映射到某个高维特征空间,然后找到半径为R的最小封闭超球体,可描述为下列最优化问题,即

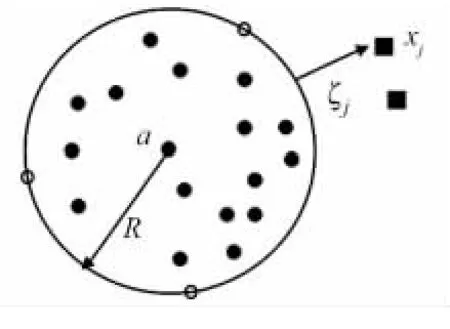
图1 二维空间最优超球体示意图Fig.1 Optinal sphere schematic diagram of two-dimensional space
式(1)中:C<1是惩罚因子,调节超球体,控制误差;a是球心;ξj是松弛变量.为了解决这个问题,引进拉格朗日算式
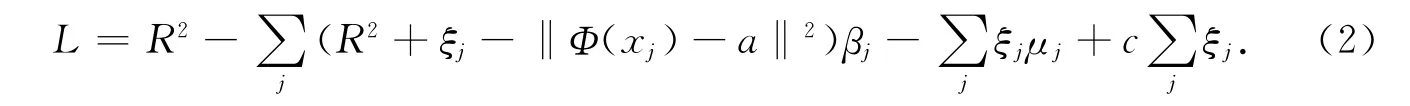
令∂L/∂R=0和∂L/∂a=0,可分别得到和最后将式(1)的问题转化为如下对偶问题,即

式(3)中:K(xi,xj)=Φ(xi)·Φ(xj)是核函数.只有满足0<βj<C的点在超球体边界,称为支持向量(support vectors,SVs).训练高斯核支持函数是用Φ(x)到球心的平方径向距离来定义的,有

式(4)中:{x∶f(x)=R2}为支持向量.
2 核函数
2.1 K型核函数
K型核函数具有泛化能力强的优点,避免了径向基核函数复杂的指数运算,同时具有多项式核函数计算量少和径向基核函数逼近精度高的优点,性能更加优越[7].K型核函数的公式为
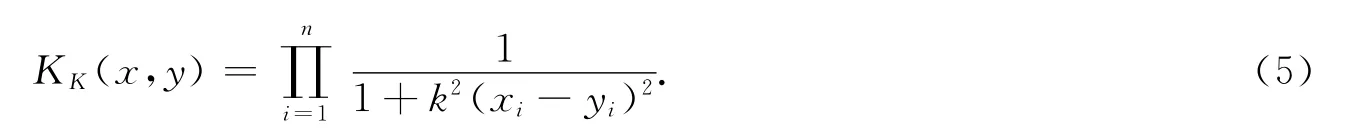
式(5)中:x=(x1,…,xn′);y=(y1,…,yn)′;k>0反映K型核函数的宽度.
2.2 指数径向基核函数
径向基核函数具有的优势,指数径向基核函数也具有,同时还具有计算量比径向基核函数少的特点.指数径向基核函数[8-9]的公式为

式(6)中:σ是核函数参数.
2.3 多核函数
为了权衡各种特征向量的差异,在单核函数的基础上,综合考虑引入多核函数.多核函数1,多核函数1的公式分别为

式(7)中:α1,α2∈[0,1]是多核函数参数;是径向基核函数.
由文献[10]可知,上述多核函数是合理的核函数.径向基核函数、K型核函数和指数径向基核函数具有各自的优势,将径向基核函数分别与K型核函数、指数径向基核函数组合得到多核函数可以将两者的优势互补.利用多核函数,可以构造出性能更加优越的SVDD算法.
3 基于核函数改进的SVDD分类算法
算法的基本思想是,利用光谱特征组合的特征向量,采用基于多核函数1和多核函数2的SVDD改进算法对遥感图像进行分类.分类的实现主要分如下3个主要阶段:1)把训练样本输入SVDD进行训练;2)用训练好的SVDD对测试样本和待分类图像进行分类;3)对结果进行评价分析.
算法的实现步骤:设标记样本集为训练集{(xi,yi)}Ni=1⊂X×Y,xi∈X表示一个输入模式,yi∈Y={ω1,…,ωc}表示对应的输出类.用SVDD算法进行多类分类的中心思想,是利用由SVDD得到的领域描述信息来估计每个类的分布,然后通过贝叶斯决策规则对数据点分类[6].
算法的训练阶段有如下3个具体步骤.
步骤1数据预处理及模型参数初始化.将提取各波段遥感图像的光谱特征组合成的特征向量作为训练集,初始化惩罚因子C=0.1,径向基核函数和指数径向基核函数的参数σ=3,K型核函数的参数k=0.001和多核函数参数α=0.01,分别在(0,1),[3,25],(0,1)和[0,1]内取C,σ,k和α,步长分别为0.1,1,0.001和0.01,使用网格搜索法[11]找到最优参数组合使得分类精度最高.
步骤2数据分区.根据输出类把给定的训练集分成c个不相交的子集{Dk}ck=1.例如,第k类数据集Dk,包含Nk个元素,即Dk={(xi1,ωk),…,(xiNk,ωk)},其中xi是第k类遥感图像的特征向量,ωk是对应的类别标签.
步骤3对每类数据集做SVDD.对每类数据集Dk,通过SVDD建立一个训练高斯核支持函数.具体是解式(3)的对偶问题,记解为,l=1,…,Nk,Jk⊂{1,…,Nk}是非零ˉβil的指标集合.每类数据集Dk的训练高斯核支持函数由下式给出
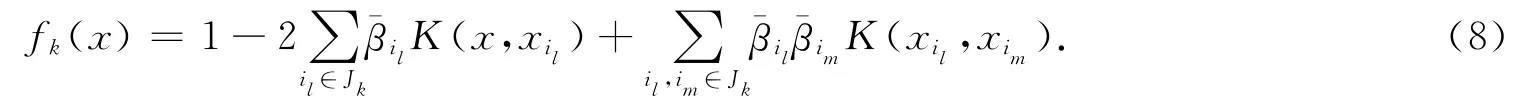
算法的测试阶段有2个具体步骤.
步骤1为每个类构造伪密度函数.即为每个类k(k=1,…,c)构造伪密度函数对任意fk(·)的支持向量xsk,rk=R2(xsk).
步骤2用估计伪后验概率分布函数进行分类.即对每个类k(k=1,…,c)估计伪后验概率分布函数为

4 仿真实验与结果分析
首先对美国Lanier lake湖区Landsat E TM+遥感图像选取波段3,4,5组合成多波段图像作为原始的遥感图像(图2(a));然后,对合成图进行降噪等预处理,并选择大小为200px×200px的图像作为待分类图像(图2(b)),再次分别提取第3,4,5波段遥感图像(图2(c,d,e))的光谱特征组合成特征向量;最后用特征向量进行训练和测试分类效果.

图2 美国Lanier lake湖区遥感图像Fig.2 Remote sensing image of American Lanier lake
参照土地利用图,采用目视解译,确定该地区地面覆盖类型为水域(W)、草地(G)、落叶林(D)、针叶林(P)、耕地(A)、居民区(U)和裸地(B).对以上每类各选取200个样本,并将其中的100个样本作为训练样本,剩余100个样本作为测试分类样本.
为了验证算法的有效性,在环境为Matlab R2010b,机器配置为Pentium(R)Dual-Core cpu T4400 2.20GHz,内存为1.93GB的计算机上进行仿真实验.利用实验得到的训练模型对分类图像进行分类,结果如图3所示.
分类精度(P)是遥感图像中正确分类的百分比,而Kappa系数(K)是用来评价分类精度的多元统计方法[12],在遥感图像处理中主要用于精确性评价和图像的一致性判断.分类精度、Kappa系数越大,分类结果越可靠,其表达式分别为
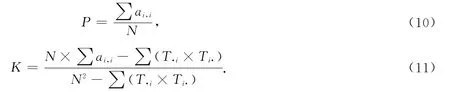
式(10),(11)中:ai,i代表分类混淆矩阵A的对角元素;N为各样本总数;Ti·和T·i分别表示A的第i行之和以及第i列之和.
从待分类图像中7类地物的每一类中分别选取100个样本点进行仿真,计算各个样本所属类别,并将每类样本分类结果数据看作矩阵,计算分类总精度(Ptot)及Kappa系数.然后,将3次实验所得的分类混淆矩阵中的总体分类精度,Kappa系数和训练时间(t)作为评价标准,结果如表1所示.
从表1可知:基于多核函数1的SVDD算法具有学习能力强、泛化能力强和计算量小的优势;基于多核函数2的SVDD算法具有学习能力强和计算量小的优势.从表1还可以看出:和基于径向基核函数的SVDD算法相比,基于多核函数1和多核函数2的SVDD算法分类精度得到提高,训练时间也减少了.其中,基于多核函数2的SVDD算法所用时间最短.
5 结束语
文中首次将K型核函数和指数径向基核函数应用于SVDD算法中,并将构造的多核函数SVDD算法应用于遥感图像分类.通过对遥感图像的分类,验证了基于核函数改进的SVDD算法缩短了分类过程的训练时间,提高了分类精度,具有较强的现实意义.
[1]TAX D M J,DUIN R P W.Support vector data description[J].Machine Learning,2004,54(1):45-66.
[2]李卫鹏,李凌均,孔维峰,等.正交小波变换支持向量数据描述在故障诊断中的应用[J].机械科学与技术,2011,30(3):466-470.
[3]成宝芝,赵春晖,王玉磊.结合光谱解混的高光谱图像异常目标检测SVDD算法[J].应用科学学报,2012,30(1):82-88.
[4]王震宇.基于支持向量数据描述的说话人识别研究[D].杭州:浙江工业大学,2011:13-50.
[5]汪廷华,赵东岩,张琼.多类核极化及其在多宽度RBF核参数选择中的应用[J].北京大学学报:自然科学版,2012,48(5):727-731.
[6]LEE D,LEE J.Domain described support vector classifier for multi-classification problems[J].Pattern Recognition,2007,40(1):41-51(doi:10.1016/j.patcog.2006.06.008).
[7]孙翠娟.基于K型核函数的支持向量机[J].淮海工学院学报:自然科学版,2006,15(2):4-7.
[8]王春燕,夏乐天,孙毓蔓.基于不同核函数的SVM用于径流预报的比较[J].人民黄河,2010,32(9):35-36.
[9]LIMA C A M,COELHO A L V,CHAGAS S.Automatic EEG signal classification for epilepsy diagnosis with relevance vector machines[J]Expert Systems with Applications,2009,36(6):10054-10059.
[10]杜培军,谭琨,夏俊士.高光谱遥感影像分类与支持向量机应用研究[M].北京:科学出版社,2012:117-118.
[11]王兴玲,李占斌.基于网格搜索的支持向量机核函数参数的确定[J].中国海洋大学学报,2005,35(5):859-862.
[12]LAM K W K,LAU W L,LI Zhi-lin.The effects on image classification using image compression technique[J].International Archives of Photogrammertry and Remote Sensing,2000,33(B7):744-750.
