高压涡轮工作叶片叶型设计研究
2014-11-19雷兹尼克亚什尼科夫霍梅列夫比卡叶尔少夫
C.B.雷兹尼克,V.I.亚什尼科夫,S.A.霍梅列夫,E.L.比卡,S.V.叶尔少夫
(1.伊夫琴科前进设计局,乌克兰扎波罗热;2.机械工程研究院,乌克兰哈尔科夫)
程 燕,陈 云,译
(中航工业沈阳发动机设计研究所,沈阳 110015)
0 引言
现代航空发动机制造业的主要趋势是在设计中提高部件气动负荷,进而降低加工、维护成本和提高结构质量,可以在不同程度上减少压气机和涡轮叶片的数量。
高压涡轮可采用跨声速和超声速的导向叶片和工作叶片。通常,由于气动参数梯度较大,存在压缩和膨胀激波之间的相互作用,以及附面层和尾迹流动,这种叶栅内的流体具有非常复杂的流动特性。直接通过试验研究上述特性成本较高,而且很多研究无法通过试验的方式开展,需要采用一些现代化的数学方法进行研究。
本文运用可靠的数值计算方法进行了叶栅型面特性研究,计算精度可以满足叶栅气动参数的确定。
1 计算方法
为了实现对工作介质物理特性的准确模拟,目前使用的半经验湍流模型基于雷诺平均Navier-Stokes算法[1]在工程上满足模拟了工作介质流动的所有现象(激波、湍流、分离流动等)和由其引起的气流参数的局部和积分的变化。
本文应用“伊夫琴科-前进”设计局FlowER程序中的2维流体模块,基于Menter的k-ω SST模型[3]实现了流动的数值计算,方程采用2阶精度隐格式差分求解[1]。涡轮叶栅叶间流路的计算网格采用H型网格,网格数为100×160,附面层网格不少于22~25,叶片表面第1层网格厚度小于1/√Re。叶型前、后缘计算网格如图1所示。

图1 叶型前、后缘计算网格
2 计算方法的验证
所使用计算方法的有效性经公开出版刊发的检测计算方法以及“伊夫琴科-前进”设计局积累的试验数据进行了验证。文献[4-6]有关叶型叶栅试验和计算结果对比分别如图2~5所示。

图2 M2is=1.19状态下涡轮叶栅流场对比
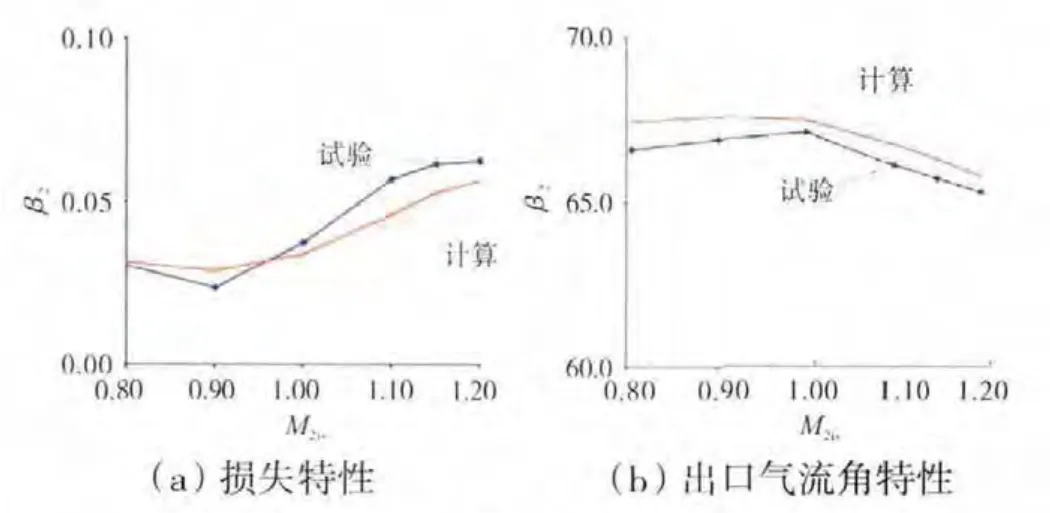
图3 叶栅1试验结果和计算结果对比
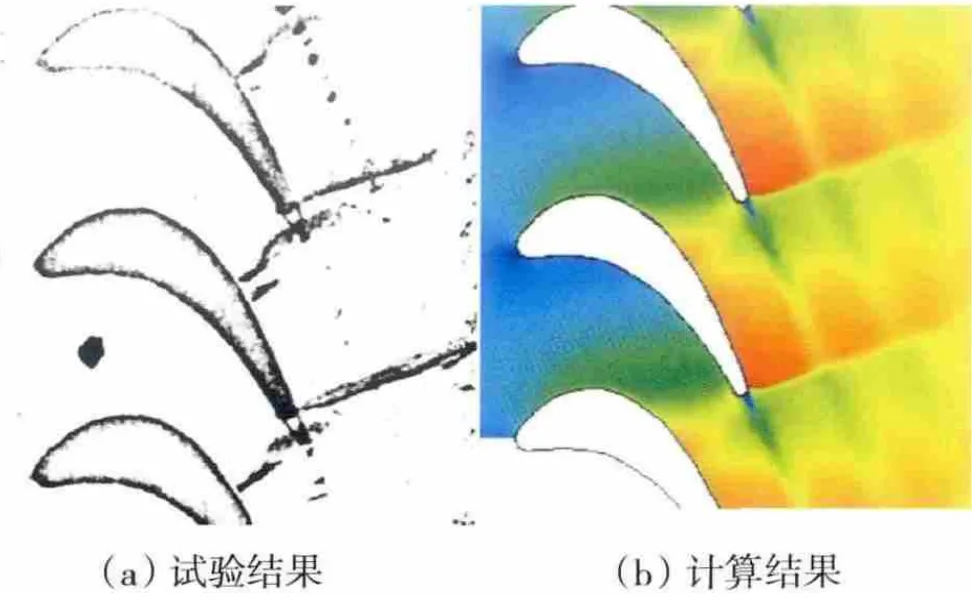
图4 М2is=0.96状态下涡轮叶栅流场对比
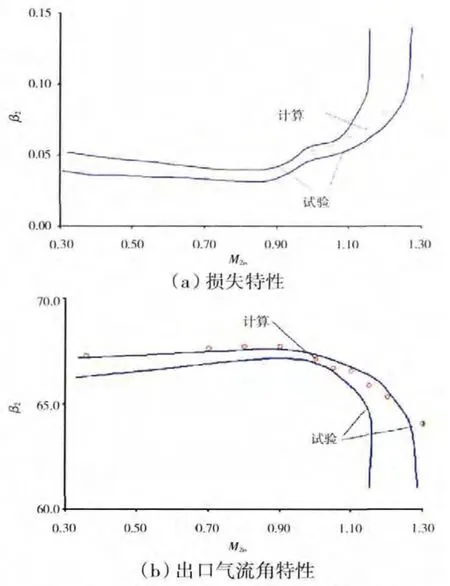
图5 叶栅2试验与计算结果对比
从上述图中可见,该计算方法准确地模拟了叶栅流场内的流动现象(激波的形成和位置,激波与叶背处附面层流动的相互作用等),并完整地再现气流积分参数的变化。对于叶栅1损失系数计算值的绝对偏差不超过1%,气流出口角偏差不超过1°。对于叶栅2损失系数及出口气流角特性计算值也都在试验范围的边界内。
3 基础叶栅的流体计算分析
运用上述方法研究了某航空发动机单级高压涡轮工作叶片中截面叶型的特性。叶型几何参数见表1,初始和优化叶型对比如图6所示,计算状态为λ2is=0.90。研究了单级涡轮落压比由πT*=2.73提高到3.05时,在该涡轮动叶叶栅内增大压差的可能性。
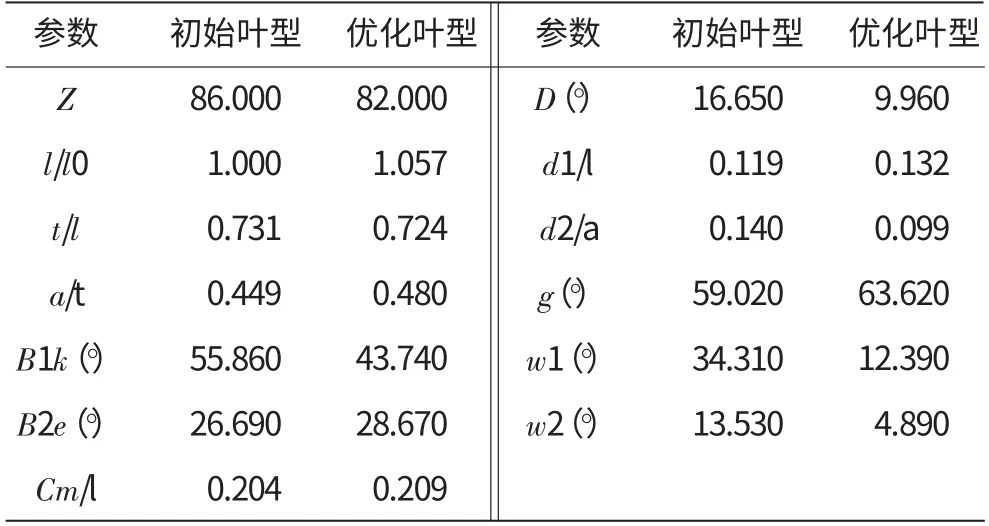
表1 叶型几何参数
λ2is=1.20时,叶栅等马赫数线对比如图7所示,叶栅尾缘绕流矢量如图8所示。从图8中可见,随着飞行高度的变化,当雷诺数减小时,叶背处斜激波后附面层出现局部分离流动,可能会发展为气流在斜切面上的明显分离流动,这必定伴随着损失的明显增加。由于叶背附面层与尾缘分离的掺混,会形成较大的尾迹流动。尾迹与叶栅内一系列压缩波及膨胀波的相互作用造成气流的能量损失进一步增加。
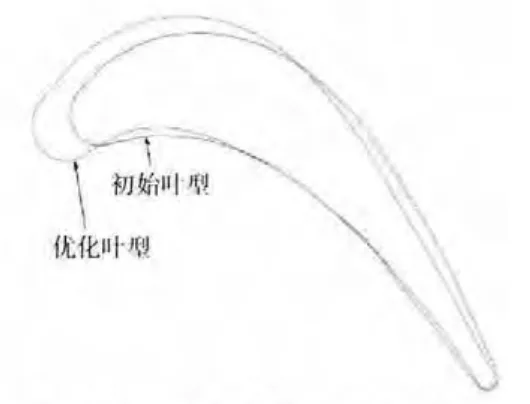
图6 初始和优化叶型对比
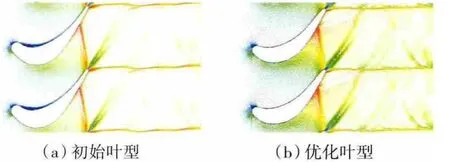
图7 λ2is=1.20叶栅等马赫数线对比
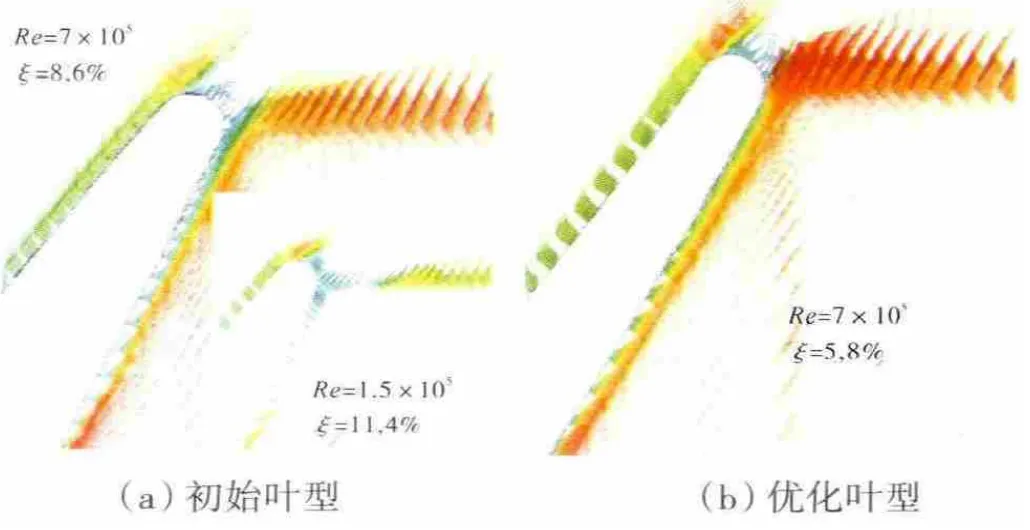
图8 λ2is=1.20叶栅尾缘绕流矢量
初始叶型和优化叶型的损失特性对比如图9所示。从图9中可见,初始叶型在这种流动特性下λ2is=1.20状态的损失比λ2is=0.90状态的高2倍。如果不进行叶型的改进设计而提高该涡轮膨胀比是不合理的,因此对涡轮工作叶片进行重新气动优化设计是非常有必要的。
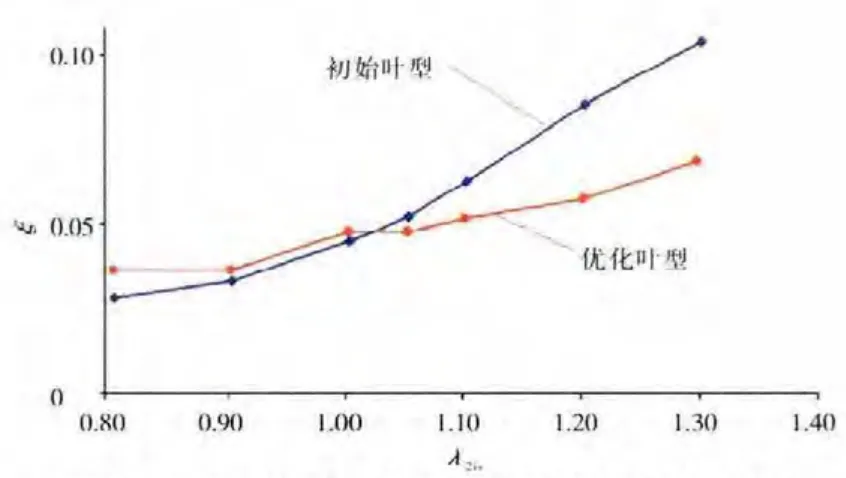
图9 初始叶型和优化叶型的损失特性对比
4 叶型气动优化结果
叶型的气动优化主要是指几何参数的变化。依照叶栅的损失水平和叶片数进行优化,来减轻质量及加工成本。使用2DFlowER黏性计算程序对重新设计的叶型方案进行分析。受冷却要求制约,新的叶型前缘较厚,尾缘较薄,有效出气角变化较小,进口构造角明显变小,尾缘楔角减小,尾缘弯折角变小,喉部后叶背型线曲率变小,喉部面积增大。
通过计算获得的损失系数与叶栅相对栅距的关系如图10所示。从图中可见,新的叶型相对栅距接近最佳值。叶型弦长相对于初始叶型长度增大的同时相对间距变化量较小,使叶栅稠度变小(叶片数量减少5%)但效率没有明显降低。
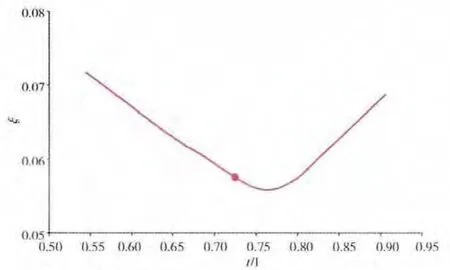
图10 损失系数与叶栅相对栅距的关系曲线
叶型表面等熵马赫数分布对比如图11所示。从图11中可见,叶型表面绕流特性的变化主要表现在载荷的重新分配,进、出口段的载荷减小了,型面中部的载荷增大了。
在亚声速绕流状态下,优化后叶型显然是小载荷的,该变化导致叶栅出口段亚声速气流的流动范围和强度增大,使得叶型损失相对于初始叶型有所增大,如图11(a)所示。
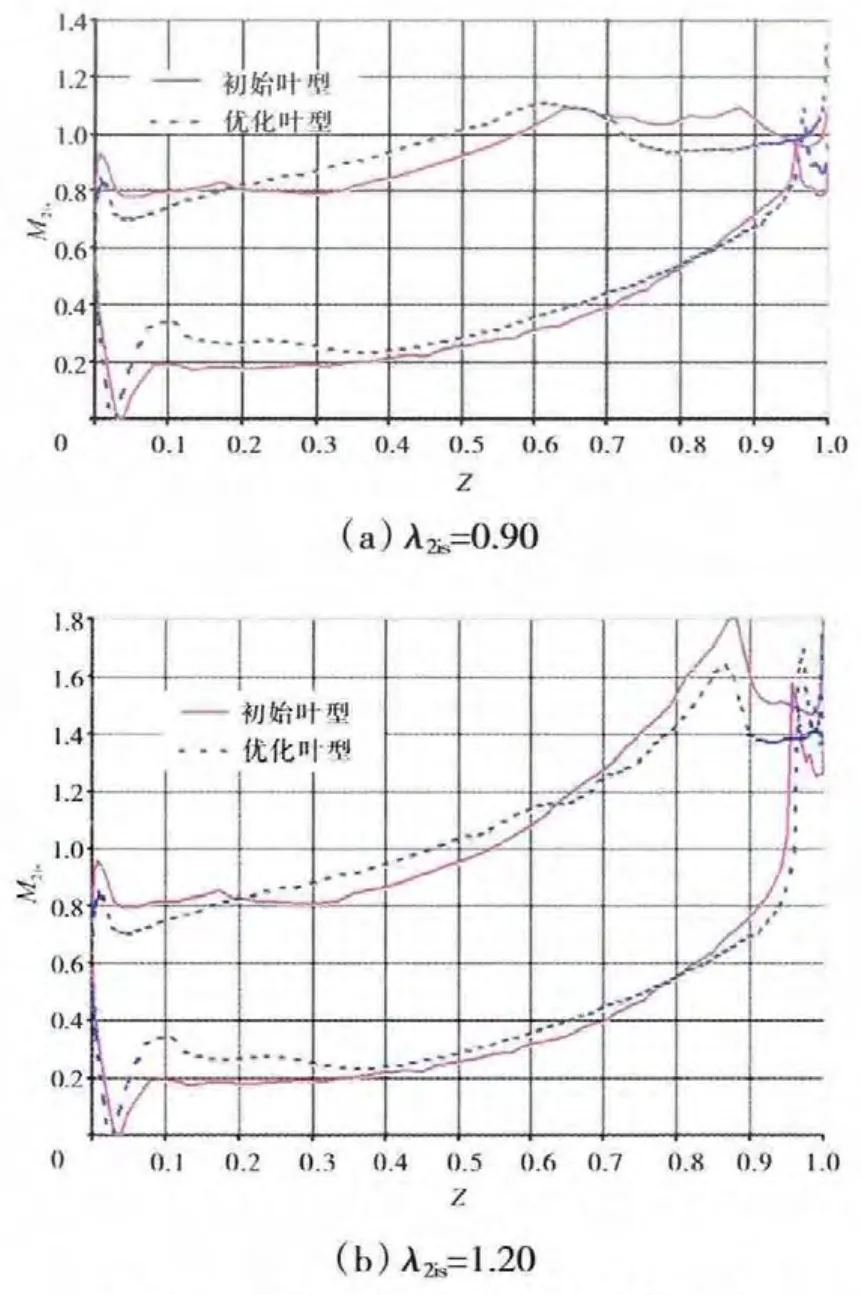
图11 叶型表面等熵马赫数分布对比
随着工作状态的提高,优化后叶型可以保证气流沿叶背更为均匀的加速,从而避免在斜激波后的尾缘处发生气流分离,减弱了尾迹流动。这种叶型修改的积极效果在于明显减小了损失系数(由8.6%减到5.8%),如图11(b)所示。
综上所述,新的叶型在所研究的整个工作状态范围内损失变化更为平缓。该叶型在亚临界或超临界压差下都具有较高的效率。另外,计算数据表明,优化后的叶型对于进一步提高工作状态具有一定的储备。
改进后的叶型的缺点是在叶盆侧的进口边还存在一定的分离流动,该分离区的形成需要进一步限制,便于冷却设计而采用的较厚的前缘厚度。
根据以上结果对叶型开展了进一步优化。前缘厚度增大2.5%,前缘楔角从12.4°增大到23°,在所研究的工况范围内基本上成功消除了气流分离(如图12所示),但叶型总效率的提高并不明显。主要原因是在叶型前缘气流速度相对较低,因此,能量损失总体水平比例不明显。另外,这种气动优化增大了2%以上的叶型截面面积,增加了叶片质量,所以,在目前这一阶段叶型不是最优的,但可以作为后续研究的对象。

图12 叶型面进口段重新造型消除分离区域
5 结果确认
在“前进”设计局开展了平面叶栅吹风试验,以对优化叶型的平面叶栅试验件气流参数的测量结果进行验证,如图13所示;叶栅的损失特性得到了验证,如图14所示。在所研究的换算速度范围内,测量的损失系数均未超过计算值,从而验证了该叶型具有较高的效率。
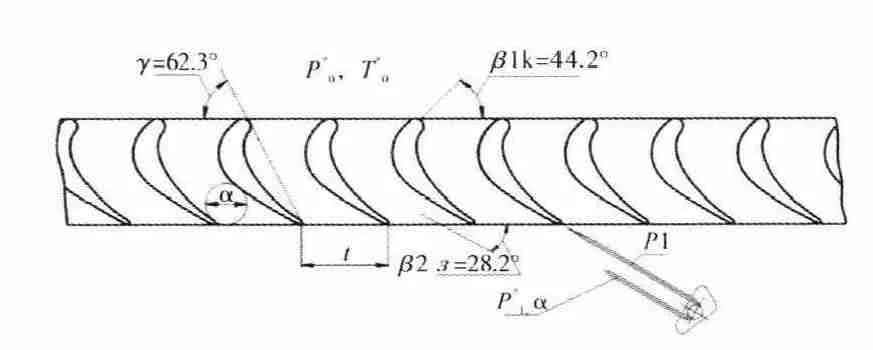
图13 平面叶栅试验件气流参数测量
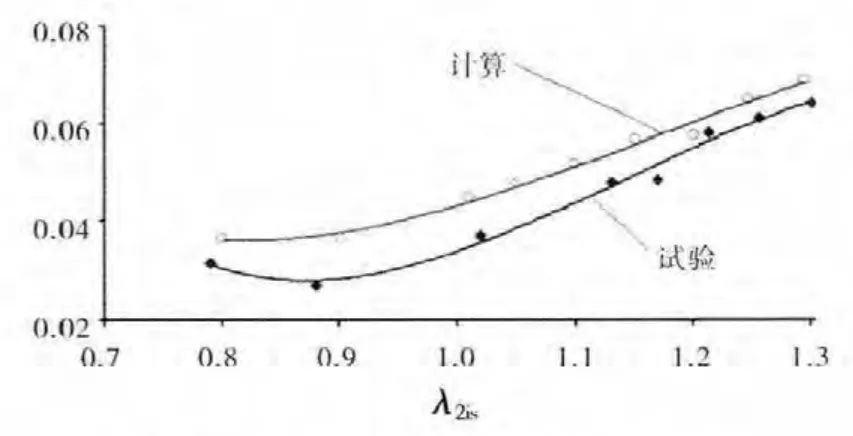
图14 优化叶栅的损失特性
6 结论
(1)提高部件气动负荷可以降低航空发动机的成本和结构质量。
(2)在设计高压涡轮叶型时应广泛运用现代数学研究方法,即可压气体黏性流计算方法。
(3)用FlowER程序对2维流体计算方法的校核表明,该方法计算的效率及其在工程上应用是可行的。
(4)使用燃气黏性流体2维计算方法对航空发动机高压涡轮工作叶片叶型进行了优化设计。经与初始叶型对比,优化叶型在各状态下损失特性变化更为平缓,并且在超临界状态时效率更高。与初始叶型相比,在λ2is=1.20状态下的损失减少了2.8%。
(5)通过平面叶栅吹风试验对叶型的优化计算结果做了验证。在各研究状态下测得的损失系数均未超出计算值。
致谢
向参与本研究工作的“伊夫琴科-前进”设计局试验研究部主任设计师U.A.法金先生表示感谢!
[1]Boiko A V,Govorushenko U N,Yershov C V,et al.Aerodynamic calculation and optimization design for the flow path of turbine machine[R].KHPI-2002-4-324.
[2] Yershov S V, Rusanov A V,Yershov S V. 3D gas flows solver complex for multi-rim turbomachines"FlowER" [R]. Ukraine:State Agency of Ukraine on Copyright and Related Rights,1996.
[3] Menter F R.Two-equation eddy viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(11):1299-1310.
[4] Sui L,Denton J.Sui L.Bottom pressure and losses in a group of four arrays of turbine blades[J].Modern Engineering,1989,(1):12-21.
[5] Haller B, Camus J. Haller B. Increase aerodynamic losses caused zavesnym cooled transonic turbine blades [J]. Energy Machine,1984(1):117-124.
[6]Kiock R,Lehtaus F,Baines N C,et al.The transonic flow through a plane turbine cascade as measured in four European wind tunnels[J].ASME,1986,108:277-284.
