博弈论科学文献的可视化分析

李 杰，吕鹏辉，郭晓宏

（1．首都经济贸易大学 安全与环境工程学院，北京 100070；2．武汉大学 信息管理学院，武汉 430072）

博弈思想的产生历史久远，通常认为可追溯到2 000多年前的我国古代文献记载的田忌赛马。但直至20世纪初，齐默罗（Zermelo）和波雷尔（Borel）对象棋博弈等问题的研究，才开启了博弈论系统性研究。博弈论的研究以数学、物理学、心理学等学科为依托基础，主要用以分析和解决经济学、管理学、社会学等方面的实际问题。目前，博弈论已经成为经济学研究的一个重要分支和前沿领域，同时也不断向其他研究领域在渗透。特别是1994年－2012年十八年间（1994，1996，2001，2002，2005，2007，2012）就先后有7届诺贝尔经济学奖授予了16位在博弈论研究方面的科学家。诺贝尔奖授予博弈论的研究学者充分说明了使用博弈论解决经济问题的有效性。科学知识图谱方法（或称信息可视化）的方法近年来随着计算机数据库技术和数据处理技术的发展已经具备对大量科学文献进行分析，从而提炼和分析科学的发展情况的水平。科学知识图谱是以显示科学知识发展进程与结构关系的一种可视化显示手段，是科学计量学最有前景的研究方向之一。就国内而言，各个领域的相关研究人员已经根据计算机可视化技术绘制成了科学学与管理学、现代工程科学技术以及科学技术研究等知识图谱，在很大程度上帮助所在领域研究人员梳理和明确了本学科的发展态势［1］。通过文献调研专门就博弈论相关的文献计量或指知识图谱工作再国内外都尚未开展。在此背景下，为了更加深入地认识博弈论的研究态势，本文运用了科学知识图谱的方法从博弈论研究国际力量的分布、博弈论研究的作者分析、博弈论研究关键词的热点探测和文献共被引等几个方面对博弈论的研究情况进行了分析和讨论。本文通过博弈论科学文献的可视化分析，以期对博弈论研究态势有一个全面的认识，并为相关研究人员提供研究参考。

一、数据与研究方法

在以往研究中使用专业的权威期刊能够很好地反映学科的研究现状及热点。鉴于此，本文通过web of science数据库检索到与博弈论直接相关且具有很强国际影响的专业期刊Games and Economic Behavior与International Journal of Game Theory。两种期刊从1996年被Web of Science收录至今（详细信息可参见表1）。其中International Journal of Game Theory 是被SCI与SSCI双收录的期刊［2，3］，以它们为研究对象可以反映博弈论研究的基本情况。

表1 博弈论国际期刊的基本信息

在Web of Science中分别以出版物名称＝（Games and Economic Behavior）与出版物名称＝（International Journal of Game Theory）进行检索，以文献类型＝（Article）为精炼依据进行精炼，剔除了Proceedings Paper，Biographical Item，Editorial Material，Book Review 等类型的文献。精炼后从Games and Economic Behavior共得到1 477条文献，从International Journal of Game Theory得到638条文献，将检索得到的文献以全记录形式导出（结果包含文章的基本信息及其参考文献）。

使用Hist Cite进行初步统计，得到的文献共包含2 115篇文献、2 061名作者和21 987条参考文献，以及2 407个关键词。将下载的数据使用Notepad＋＋做了相关处理后，导入文献可视化分析软件CiteSpace 3．5R3进行分析。CiteSpace由德雷克塞尔大学（美国费城）信息科学与技术学院陈超美教授研究开发于2004年9月，并在不断持续更新。CiteSpace是一款可用于识别学科前沿的演进路径及学科领域的经典基础文献的可视化分析软件。在CiteSpace II中是以节点和连线的方式来呈现分析结果，引文年代圆环代表这篇文章的引文历史；引文年轮的颜色代表相应的引文时间；一个年轮的厚度与某个时间分区内引文的数量成正比；节点中心旁的数字代表整个时间跨度内的被引次数，特别需要说明的是在做作者、机构以及国家的合作网络的知识图谱时，Freq指的是发文量。节点的类型可以根据需要进行选择，从而在题目、摘要中提取节点信息。

二、博弈论研究文献的时空分布

（1）时间与领域分布 图1表示了两种博弈论国际期刊的载文情况。作为刊载博弈论研究的期刊来讲，两者各有优势。近年来Games and Economic Behavior载文量有快速上升的趋势，而International journal of game theory载文量变化不太明显。相对而言International journal of game theory刊载的文章范围相对狭窄，稿源较为单一，且为季刊，因此载文量相对前者会较少。从本文的研究出发，总体上关于博弈论的研究论文数量呈上升趋势。经CiteSpace的category分析，所有文献在ISI的学科属性分布上属于Statistics ＆Probability Business ＆Economics，Social Sciences，Mathematics，Mathematical Methods In Social Sciences，Economics Business ＆Economics和Economics五大学科领域。

图1 博弈论研究的年度载文量

（2）空间地域分布和机构分布 博弈论的研究力量分布及其发文情况参见图2和图3。从图2的博弈论机构分布图上可以得到美国的西北大学（Northwestern University）、以色列的耶路撒冷希伯来大学（Hebrew University of Jerusalem）以及以色列的特拉维夫大学（Tel Aviv University）位于前三位。此外，荷兰的蒂尔堡大学（Tilburg Univ）、美国的纽约大学（NYU）、加州理工学院（Cal Tech）、哈佛大学（Harvard University）以及荷兰的马斯特里赫特大学（Maastricht University）也在博弈论研究方面表现出很强的优势。

图2 博弈论研究的机构发文量

图3显示了博弈论研究主要国家的分布。美国（USA）、以色列（Israel）、西班牙（Spain）、荷兰（Netherlands）、英国（England）、德国（Germany）、法国（French）和加拿大（Canada）的发文量均大于100篇，这与研究力量的机构国别分布具有很强的相关性。此外，通过对国家的中心性进行测度，德国（Ger－many）、荷兰（Netherlands）、加拿大（Canada）、澳大利亚（Australia）、美国（USA）以及西班牙（Spain）等国家有较强的中介中心性，反映了这些国家不仅在国际博弈论研究中有很强的优势，而且这些国家在参与国际间博弈论合作研究上有重要作用。我国（包含港、澳在内，也包括与国外研究机构合作的文章）的博弈论研究在这两种期刊上发文共计28篇，在合作对象上仅仅与荷兰、加拿大、韩国以及澳大利亚等几个国家有合作，因此我国在研究实力和参与国家间的合作程度上都存在不足，需要在今后的研究中主动寻求国际合作伙伴，大力提高自己的研究水平尤其是高水平博弈论的论文成果。

图3 博弈论的国家发文分布

三、国际论文的作者共被引分析

作者的共被引分析是指不同作者同时出现在施引文献中的现象。通过作者的共现分析可以得到博弈论研究领域有影响力的作者及其合作群体。对研究文献的作者共被引分析结果参见表2和图4。结合这些图表不难看出，这些作者都是在博弈论或者经济学研究中具有国际知名度的研究人员。

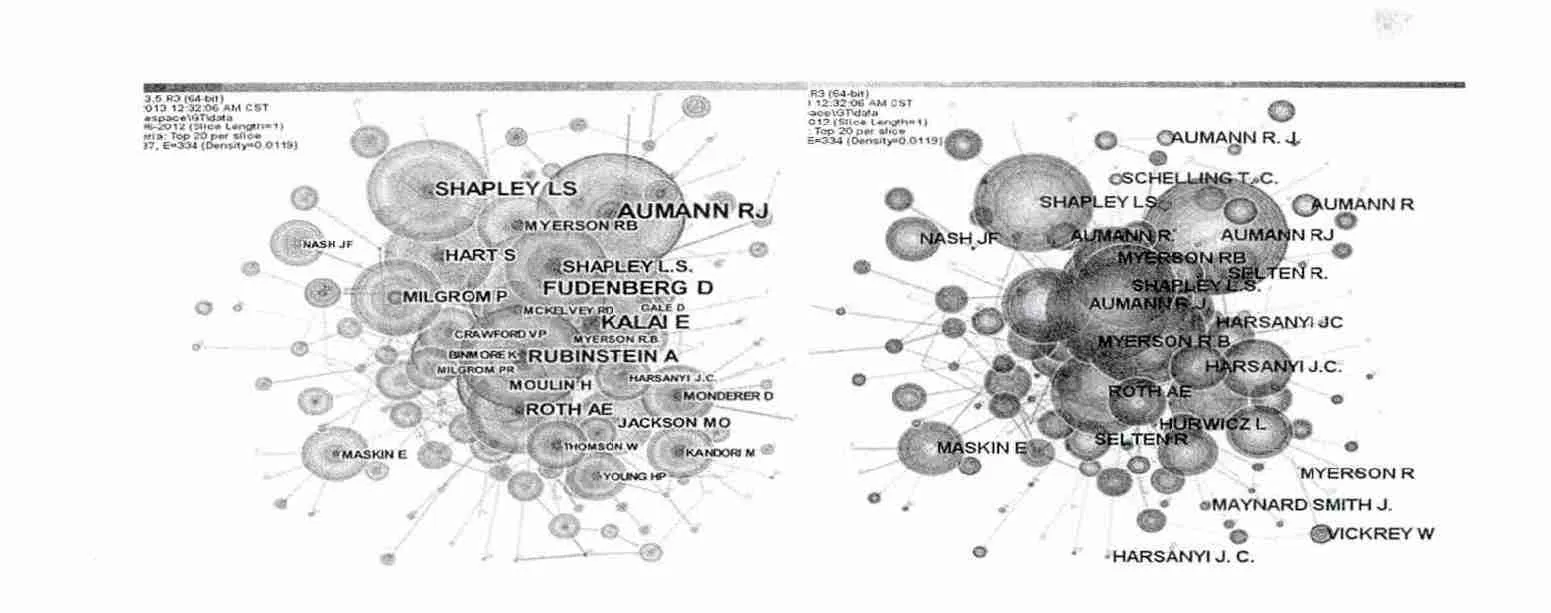
图4 作者的共被引网络

同时本文经过使用诺贝尔奖得主的姓名进行探测，其中不乏有多位诺贝尔奖获得者出现在网络中（图4右侧已标示）。其中色列耶路撒冷希伯来大学合理性研究中心教授、国际博弈论学会首任主席Robert J．Aumann的中心度和被引频次均为第一。他的主要成就表现在以下几个方面：一是第一个定义了博弈论中的相关均衡概念，这是一种非协作型博弈中的均衡，比经典纳什均衡更加灵活；二是交易者连续统市场经济模型；三是交互环境中代理人之间通识的数学公式表示；四是重复博弈的连续交互模型。而且他使用博弈论分析犹太法典中的塔木德难题，解决了长期悬而未决的遗产分割问题［4，5］。因此他也与Thomas C．Schelling一起分享了2005年诺贝尔经济学奖。此外Fudenberg D，Shapley LS和Kalai E等人在博弈论研究方面的文献也有很大影响。

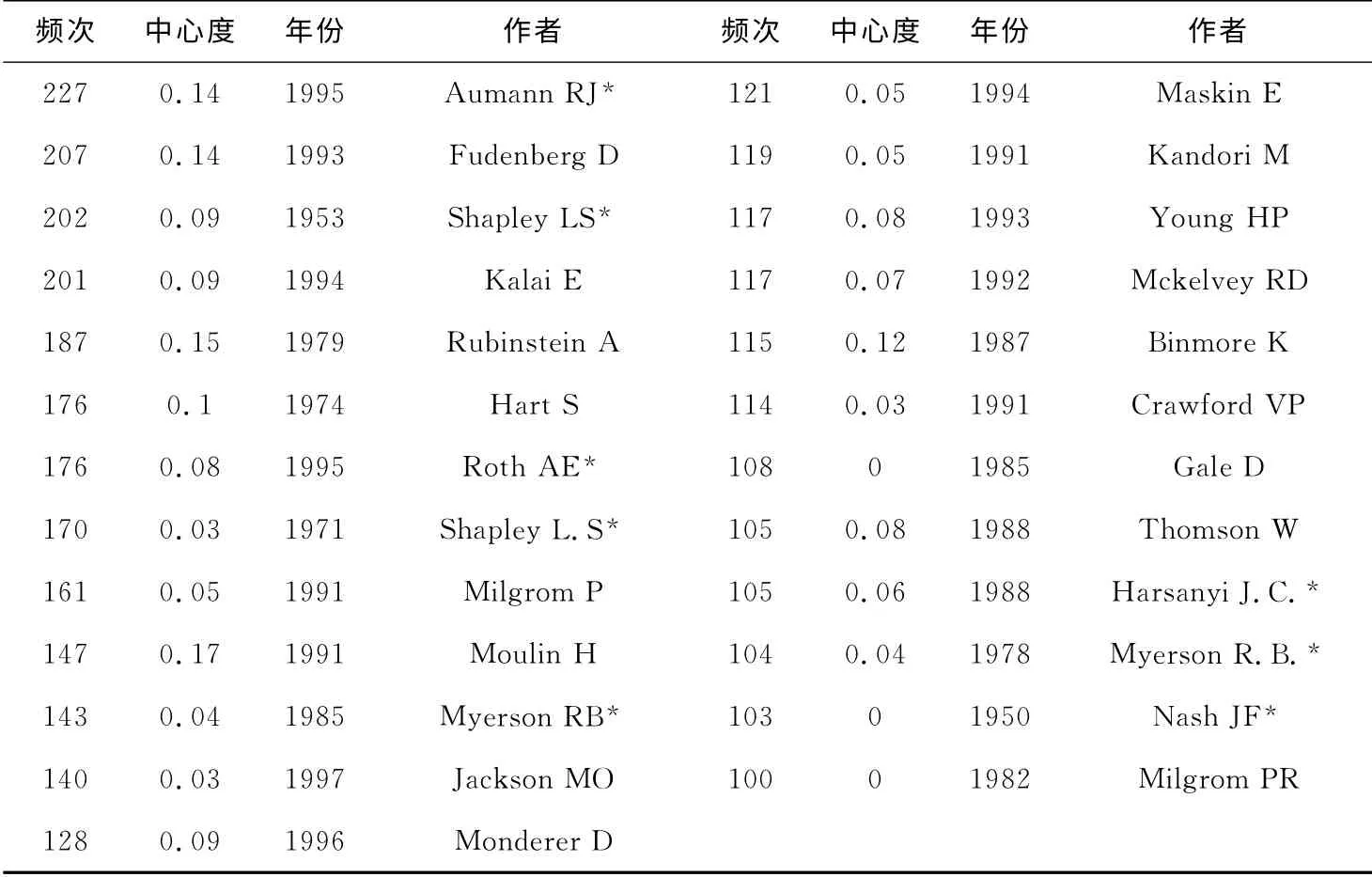
表2 作者被引频次排序（≥100）

四、研究热点与知识基础分析

（1）博弈论研究热点分析 关键词的共现网络分析是一种基于文本内容的分析方法，CiteSpace分析词汇共现是从施引文献中抽取高频关键词，抽取的高频关键词代表了这个领域的研究热点。共现次数是指从对象文件中抽取的关键词的出现次数，这在一定程度上可解释研究热点。此外，中心度是指在网络中具有关键作用的节点。这个指标反映了节点在整个网络中的“媒介”作用，即目标节点占据其他两个节点之间最短路径的能力，占据这些关键位置越多，那么其中心度就越大。

图5 博弈论研究的关键词共现网络

本文的主要分析指标为共现频次和单个节点的中心度，设定阈值为Top 50后，并运行计算生成了节点N＝255，连线E＝626的共现网络，共现网络参见图5，详细信息参见表3。图中最大的节点为博弈（Games），此外均衡（equilibrium）、模型（model）、信息（information）、核（core）等关键词也显著高于其他关键词，图5中的标签按照中心度对关键词进行了显示。可以看出，博弈（games）与核（core）的中心度都为0．18，居于首位。此外，纳什均衡（Nash－equilibrium，0．15）、模型（model，0．14）、稳定性（stability，0．14）、均衡（equilibrium，0．13）、信息（information，0．13）以及演化（evolution，0．11）等词汇具有高的中心度。

由于表3中筛选的是频次大于40的词汇，而共同知识（common knowledge，频次33，中心度0．07）作为博弈论研究的重要问题在图谱中进行了显示。核（Core）、纳什均衡（Nash－equilibrium）、均衡选择（equilibrium selection）、不完全信息（incomplete information）、重复博弈（repeated games）、夏普里值（Shapley value）等关键词不仅反映了博弈论研究的关注点，而且在一定程度上说明了博弈论的进展。如1952－1953年期间L．S Shapley 和D．B Gillies提出了核（core）作为合作博弈的一般解概念，此外L．S Shapley还提出了合作博弈的夏普里值（Shapley value）的概念［2］。

综合以上两方面的指标可以判断所选文献在研究时间内的热点及研究内容主要体现在博弈的均衡、信息以及稳定性等方面的研究。博弈（Games）作为最大的节点，有很高的频次和中心度，这反映了所选期刊和在其上刊载文章的主题。进一步的研究与其相连线的主要高频词还有Nash－equilibrium，evolution，stability，information，model，fairness，core，preference，Behavior，equilibrium selection以及existence等。这些词语与Games共同组成了博弈论研究关注的重点。此外，其他高频次和中心度的节点相互之间亦具有多条连线，进一步反映了本研究提取的关键词能代表博弈论研究的热点问题。

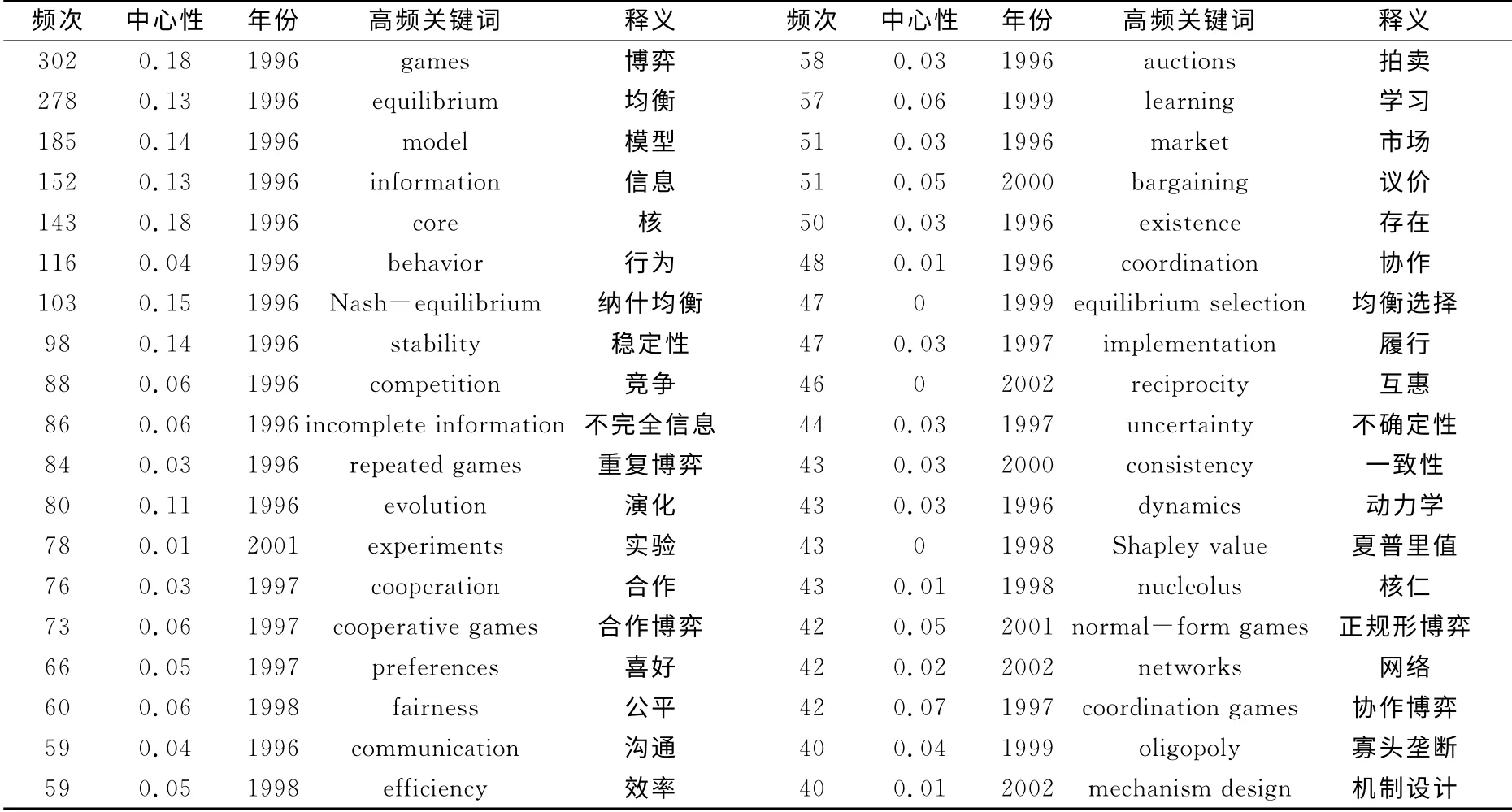
表3 博弈论研究关键词频次排序（≥40）

（2）博弈论的知识基础分析 知识基础是一个有利于进一步明晰研究前沿本质的概念，如果我们把研究前沿定义为一个研究领域的发展状况（如研究思路），那么研究前沿的引文就形成了相应的知识基础。陈超美教授将研究前沿的知识基础重新定义为研究前沿在文献中的引用轨迹［3］。

在CiteSpace中以共被引网络的形式呈现，并以中介中心性显示了重要文献，参见图6。通过进一步分析，具有重要影响的这些文献大多数是曾经因博弈论方面研究成就而获得诺贝尔经济学奖的经济学家。这些文献对博弈论的发展以及应用产生了重要影响，在此可以认为是这些文献组成了博弈论研究的知识基础。值得思考的是在节点搜索中未发现2001年诺贝尔经济学奖得主George A．Akerlof，A．Michael Spence和Joseph E．Stiglitz的文章，原因还需进一步探究。

由于全部标示诺贝尔奖获得者的文献较多，会引起图谱的不清。因此仅仅对2012年诺贝尔经济学奖得主，美国经济学家——哈佛大学教授埃尔文·罗斯（Alvin E．Roth）和加州大学洛杉矶分校教授罗伊德·沙普利（Lloyd S．Shapley）进行了标注，进一步的研究可参考标注以获取全文。此外，虽然共被引网络不能显示出研究前沿，但是它们显示了研究前沿的发展轨迹。比如在网络生成以后，点击“Cited Bursts”使得突显的文献加上了红点，这些文献是研究前沿的留下的痕迹。

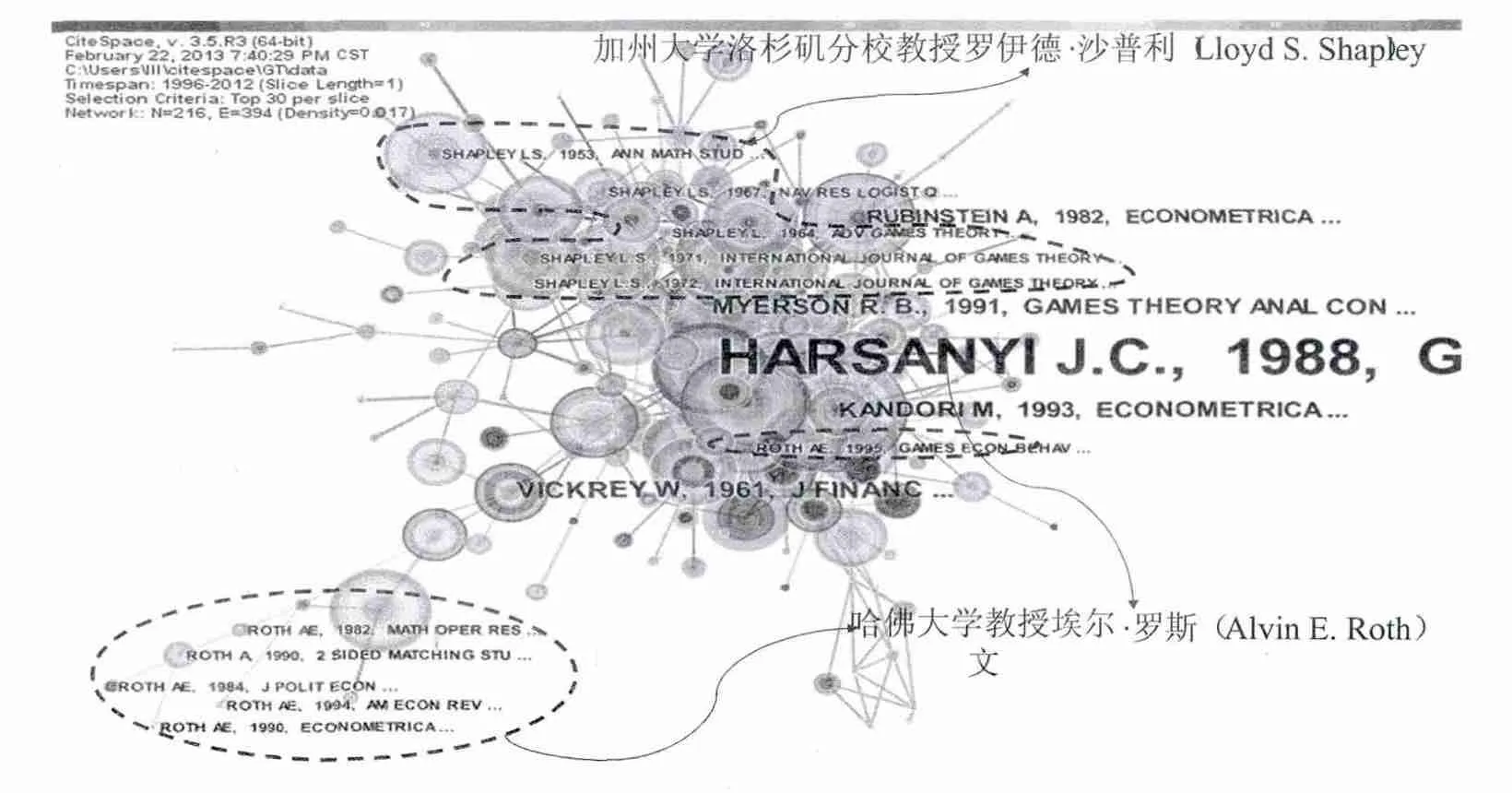
图6 博弈论研究的共被引知识图谱

为了更加深入地了解关键点文献的信息，本文对关键节点的文章进行了整理，如表4（中介中心度＞0．15），并对节点相关信息做进一步分析。

表4 共被引网络图谱关键节点信息

John C．Harsanyi（1920－2000）是美籍匈牙利人，主要贡献在于贝叶斯博弈（Bayesian games）——不完全信息博弈、功利主义伦理学（Utilitarian ethics）、均衡选择（Equilibrium selection）等方面。其生前工作对博弈论在经济学领域的应用有重要意义和影响。1994年他与John F．Nash JR．，Reinhard Selten共同获得诺贝尔经济学奖。博弈均衡选择的一般理论（A general theory of equilibrium selection in games）是其1988年与诺贝尔经济学得主塞尔腾（Reinhard Selten）的合著，是其重要研究贡献均衡选择（Equilibrium selection）的有机组成部分，该著作成为之后均衡选择理论研究的基础，为均衡选择理论的发展产生的深远影响。William Vickrey（1914－1996），加拿大人，就职于哥伦比亚大学，其主要学术贡献在于对维克里拍卖、收益等价定理以及拥挤定价的研究，他以其在不对称信息条件下的经济激励理论获得1996年诺贝尔经济学奖。Kandori，Michihiro毕业于斯坦福大学经济学，就职于日本东京大学经济研究科，主要研究微观经济理论和博弈论［9］。1993年发表于Econometrica的名著Learning，mutation，and long run equilibria in games（Google Scholar被引1 735次），很具参考价值。Ariel Rubinstein是一位研究博弈论的以色列经济学家，1972－1979年就读于耶路撒冷希伯来大学，2006年起任特拉维夫大学经济学院教授、纽约大学经济系教授，1982年他出版了“Perfect equilibrium in a bargaining model”，在Google Scholar被引4 241次（数据更新时间2013－02－24），其作品对讨价还价理论有重大贡献［10］。Roger Myerson（1951－），现就职于美国芝加哥大学，1976－2001年间在美国西北大学就职期，从事了机制设计方面的研究，并因此在2007年与Leonid Hurwicz，Eric S．Maskin获得诺贝尔经济学奖。本节点显示的是其于1991年发表的《选举制度的有效性，减少政府腐败：一个博弈论的分析》（Effectiveness of electoral systems for reducing government corruption：agame－theoretic analysis），是其重要的代表作之一。综上所述，这些重要文献反映和促进了博弈论的发展，对博弈论相关理论的发展具有重要基础作用。

五、结论与展望

通过对国际博弈论文献的分布、作者情况以及研究热点等方面的科学知识图谱分析，得到以下几点结论：第一，博弈论的研究从两大国际期刊综合载文反映出文献量有上升趋势，博弈论的研究主要集中在美国、以色列、荷兰、德国等国家。且在合作力度上，也主要集中在研究实力较强的国家之间。我国在参与国际博弈论研究上比较薄弱，表现在发文量在两个代表性的期刊上仅为28篇，且在国际合作中仅仅与4个左右的国家进行过合作。因此，为进一步提升研究实力和影响力需要积极参与国际间博弈论研究的合作以及出版更多的高质量博弈论研究成果。第二，作者共被引显示了一批在博弈论研究领域具有很大影响的学者，并独立显示了诺贝尔经济学奖获得者在网络中的位置，他们对博弈论在不同方面的进展发挥了深远的影响。第三，关键词共现网络得到了博弈论研究关键性词汇的出现频次以及在网络中的重要性。这些关键词是博弈论研究的基础词汇，也反映了博弈论研究的热点话题。在文献共现网络中得出了对博弈发展有长远影响的重要文献，这些文献组成了博弈论研究的知识基础，并不断在博弈论研究中发挥作用。最后，本文的数据仅仅来源于与博弈论直接相关的两本国际期刊，或存在一定的局限性，需在以后的研究中完善和修正。

［1］刘则渊，陈 悦，侯海燕．科学知识图谱方法与应用［M］．北京市：人民出版社，2008．

［2］谢识予．经济博弈论［M］．上海：复旦大学出版社，2007．

［3］Chen C．CiteSpace II：Detecting and visualizing emerging trends and transient patterns in scientific literature［J］．Journal of the American Society for information Science and Technology，2006，57（3）：359－377．

［4］Harsanyi J C，Selten R．A general theory of equilibrium selection in games［J］．MIT Press，1988．

［5］Vickrey W．On the prevention of gerrymandering［J］．Political Science Quarterly，1961，76（1）：105－110．

［6］Kandori M，Mailath G J，Rob R．Learning，mutation，and long run equilibria in games［J］．Econometrica：Journal of the Econometric Society，1993：29－56．

［7］Rubinstein A．Perfect equilibrium in a bargaining model［J］．Econometrica，1982，50（1）：97－109．

［8］Myerson，Roger B．Effectiveness of electoral systems for reducing government corruption：agame－theoretic analysis．Center for Mathematical Studies in Economics and Management Science，Northwestern University，1991．

［9］Graduate School of Economics，Faculty of Economics，the University of Tokyo［OL／EB］．（2014－01－02）［2013－02－23］．http：／／www．e．u－tokyo．ac．jp／fservice／faculty／kandori／kandori．e／kandori01．e．html．

［10］维基百科．阿里埃勒·鲁宾斯坦［OL／EB］．（2014－01－02）［2013－02－20］．http：／／zh．wikipedia．org／．