一种稳健的盲稀疏度压缩感知雷达目标参数估计方法

王超宇梅 湄朱晓华贺亚鹏李洪涛

①(南京理工大学电子工程与光电技术学院 南京 210094)②(中国空间技术研究院微波遥感与数传技术研究所 西安 710000)

1 引言

近年来，利用信号的稀疏性和可压缩特性进行信号检测与处理已成为信息论和信号处理领域的一项新兴技术，广泛应用于医疗成像、模式识别、图像处理、雷达成像以及无线通信等诸多领域[1]。文献[2,3]提出的压缩感知(Compressive Sensing, CS)理论指出，当信号稀疏或可压缩时，通过求解一个范数优化问题便可从少量测量值中以较高的概率重建原信号[4]。

实际中，感兴趣的目标仅占据少量的雷达分辨单元，照射区域内雷达回波信号是稀疏的[5]，因此CS在雷达信号处理领域中的应用也得到了广泛研究。然而，传统压缩感知雷达(Compressive Sensing Radar, CSR)未考虑发射波形[6]和系统模型失配误差[7]对目标参数估计精度的影响，对应的CSR感知矩阵相干系数[8](Coherence of the Sensing Matrix,CSM)较大，感知矩阵和目标信息矢量的匹配关系[9]不理想，导致目标参数估计精度不高。文献[10]较早地将波形优化技术应用于CSR系统中，提出一种基于CS的MIMO雷达CSM极小化的波形设计方法，改善了CSR目标参数提取的能力。文献[11]推导了CSM与信号模糊函数的关系，指出针状模糊函数的信号具有较小的CSM，具有较高的CSR多维参数联合分辨能力。然而，当系统模型存在失配误差时，利用文献[10]和文献[11]方法构造的感知矩阵与目标信息矢量的失配误差依然存在，目标参数估计误差较大的问题未得到根本改善。文献[12]讨论了1l范数优化算法在感知矩阵与目标信息矢量失配时稀疏信号重构误差的上界，分析了 CS中系统模型失配误差对目标信息估计精度的影响，结果表明，感知矩阵无法准确表示目标场景时，常见 CS算法对稀疏信号的重构性能劣化非常明显。文献[13]通过增加测量次数和稀疏基矩阵分辨力的方法，降低了系统模型失配时稀疏信号重构的误差，但随着稀疏基矩阵分辨力的提高，CSR系统的CSM也会随之变大，导致可检测目标个数下降以及噪声抑制能力减弱等问题。

本文针对感知矩阵和目标信息矢量失配时CSR距离-多普勒参数估计性能下降的问题，提出了一种稳健的盲稀疏度[14]CSR目标参数估计方法。首先建立了系统模型失配时的距离-多普勒2维参数稀疏感知模型；其次，考虑到CSR采用传统雷达发射波形时感知矩阵列相干系数较大的问题，推导了最小化CSM 的波形优化目标函数，并通过模拟退火[15](Simulated Annealing, SA)算法对以多相编码信号作为发射波形的目标函数进行优化求解；随后，提出一种新的盲稀疏度CSR算法，在多个快拍条件下通过发射波形，系统模型失配误差和目标信息矢量的相互迭代，逐步校正和优化对应感知矩阵，最终以较高精度重构距离-多普勒参数。本文方法克服了常见 CSR算法必须已知信号稀疏度先验信息的局限性，提高了系统模型失配误差存在时目标参数估计的精度，增强了CSR的战场环境适应能力。

2 CSR系统稀疏感知模型

2.1 距离-多普勒2维参数稀疏感知模型

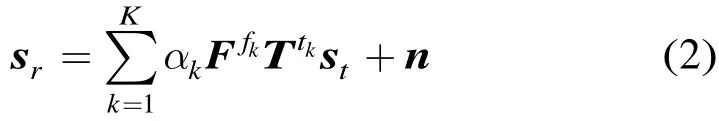
2.2 系统模型失配下的稀疏感知模型

一般情况下，CSR系统通过均匀量化相应参数获得感知矩阵，实现对目标区域的表示。然而现实中无法保证目标准确地出现在 CSR系统分辨单元的网格上，导致OTFB矩阵无法准确表示目标场景，引起感知矩阵和目标信息矢量的失配，极大影响了CSR目标参数估计的准确性和有效性。

由式(3)可知，当目标距离-多普勒参数与 CSR系统模型失配时，系统预设的与理想时延矩阵仅个别非零元素位置发生变化对系统模型影响不大；较理想频移矩阵忽略了由多普勒失配误差引起的频移项，对CSR系统模型影响较大。故假设照射区域内K个低速运动的点目标随机分布在距离分辨单元的网格上，但第k个点目标的速度与CSR系统预先设定的速度分辨单元网格失配，即。

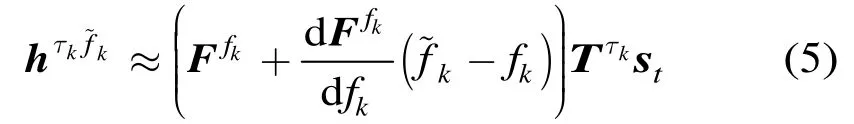
故不考虑信道干扰及接收机噪声的近似误差时，系统模型失配下的稀疏感知模型可表示为

3 CSR波形优化

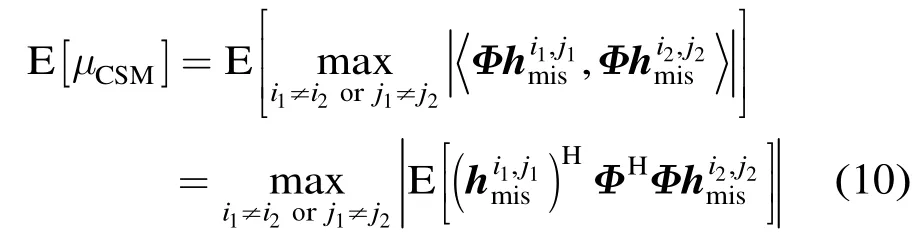
考虑到Φ为高斯随机矩阵，其元素,ijΦ服从均值为0，方差为1/L的独立同分布复高斯随机变量，容易推出矩阵中元素服从均值为，方差为的分布；服从均值为0，方差为的随机分布，由此式(10)可改写为

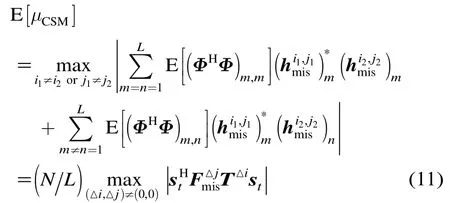
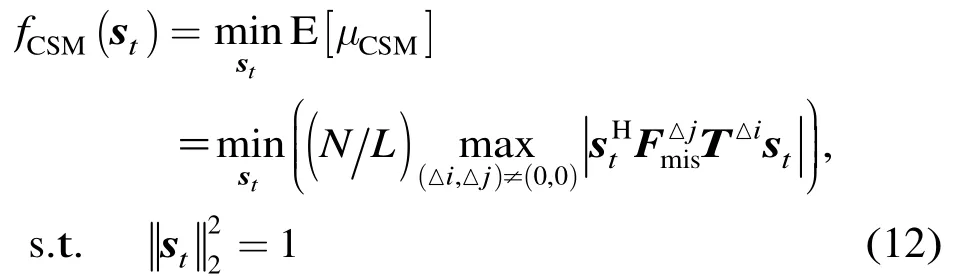
式(12)是典型的离散非线性多变量优化问题，目前解决此类优化问题的方法有神经网络算法，粒子群优化(PSO)算法和模拟退火(SA)算法等。其中，SA通过模拟物理力学系统降低系统内能时状态变迁的物理过程，优化求解复杂多变量的目标函数，较好地解决了寻求最优时陷入局部解的问题，在实际中得到了广泛应用。

为了充分利用发射机的发射功率，避免放大器非线性对发射波形的影响及昂贵放大器的使用，实际应用中发射波形多采用恒模信号，因此本文选取具有复杂相位结构，优良抗干扰和低截获概率特性的多相码信号作为发射波形，其复包络可表示为

步骤1 初始化：给定初始温度T，相位变化总个数P，码长L，随机产生初始相位编码信号s~；

4 系统模型失配时的盲稀疏度目标参数估计方法

根据上述分析可知，在感知矩阵和目标信息矢量匹配的条件下，优化式(12)得到的多相编码信号对应的感知矩阵非相干性能最优，能够保证CSR进行目标检测和参数估计的有效性。然而，当CSR系统感知矩阵与目标信息矢量失配时，该波形无法克服系统模型失配误差对目标参数估计精度的影响。同时，传统CSR算法优化求解欠定性方程组时未考虑系统模型失配误差的影响，无法保证目标参数估计的有效性和稳健性；并且传统CSR算法需要已知信号稀疏度K的先验信息[17]，严重制约了CSR系统在战场环境中的适用性。

针对上述问题，本文提出一种稳健的盲稀疏度CSR目标参数估计方法，具体步骤如下：

步骤2 波形优化：采用 SA算法优化式(12)获得对应发射波形，构造非相干性最优的感知矩阵lA；利用优化后的发射波形对 CSR感兴趣区域进行探测，令初始余量；

步骤4 识别：在感知矩阵lA各列中寻找与残差相关性最大的个列对应的序号，即，其中表示集合中个最大元素对应的序号由小到大排序后的集合；

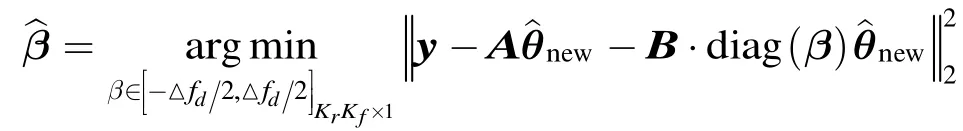
本文所提 CSR目标参数估计算法迭代过程主要由3部分组成。第1部分(步骤3~步骤7)为盲稀疏度CSR目标参数估计过程，该部分通过弱匹配原则和正则化准则分别对候选原子集进行扩充和筛选，提高候选原子集的准确率；随后，采用阶段转换的方式自适应地调整当前步长，在稀疏度先验信息未知的条件下使所选原子数目逐步逼近稀疏度，以重构出目标散射系数矢量。第2部分(步骤8)为系统模型的校正，该部分充分利用系统模型失配误差向量β的稀疏性，通过Lasso算法对其重构；随后，依据β的估计结果，对 CSR感兴趣区域的距离-多普勒参数进行校正，提高CSR系统模型对目标场景表示的准确度。第3部分(步骤2)，根据重新量化的CSR相关参数，采用波形优化的方法构建非相干性最优的感知矩阵；同时，利用对应发射波形探测CSR感兴趣的区域。最终，本文方法在多个快拍条件下迭代出较高精度的距离-多普勒参数。

5 仿真及结果分析

实验 1 距离-多普勒成像输出对比。假设在雷达探测环境中有5个随机分布在CSR分辨单元的目标，对应距离-多普勒分辨单元分别为，每个目标的散射系数服从均值为 0，方差为 5的复高斯分布，CSR回波信噪比为SNR 10 dB= 。图 1为CSR采用伪随机多项码信号作为发射波形，通过CoSaMP[12], OMP[1]以及 ROMP[6]等算法与本文方法进行距离-多普勒成像输出对比，其中“o”表示目标所在距离-多普勒分辨单元，“*”表示 CSR算法对目标所在距离-多普勒分辨单元的估计结果。

从图 1可以看出，当目标无法准确地出现在CSR预先设定的网格上时，系统预先构造的感知矩阵和目标散射系数矢量失配，使得CoSaMP, OMP以及 ROMP等算法在更新稀疏信号支撑集过程中出现识别错误，无法在有限次迭代过程中优化出合理的估计值，导致目标散射系数估计误差变大，距离-多普勒成像质量较低。相比而言，本文方法在未知信号稀疏度先验信息的条件下性能更优，得益于其利用多个快拍数据交替迭代发射波形，系统模型失配误差和目标散射系数矢量，逐步校正了CSR系统对感兴趣区域距离-多普勒参数的量化结果，改善了感知矩阵和目标散射系数矢量之间的匹配关系，提高了算法识别稀疏信号支撑集的准确性，使得本文方法能够以较高的精度估计所有目标，保证了C S R 系统参数估计的有效性和稳健性。

实验 2 目标散射系数估计RMSE分析。假设CSR感兴趣区域内距离-多普勒分辨单元和目标参数的设置均与实验1相同，回波信噪比变化范围为。图2给出了CoSaMP, OMP,ROMP和本文方法在不同信噪比条件下目标散射系数估计均方根误差的500次蒙特卡洛仿真实验结果对比。图3给出了不同信噪比条件下，本文方法对系统模型失配误差估计均方根误差的500次蒙特卡洛实验结果。

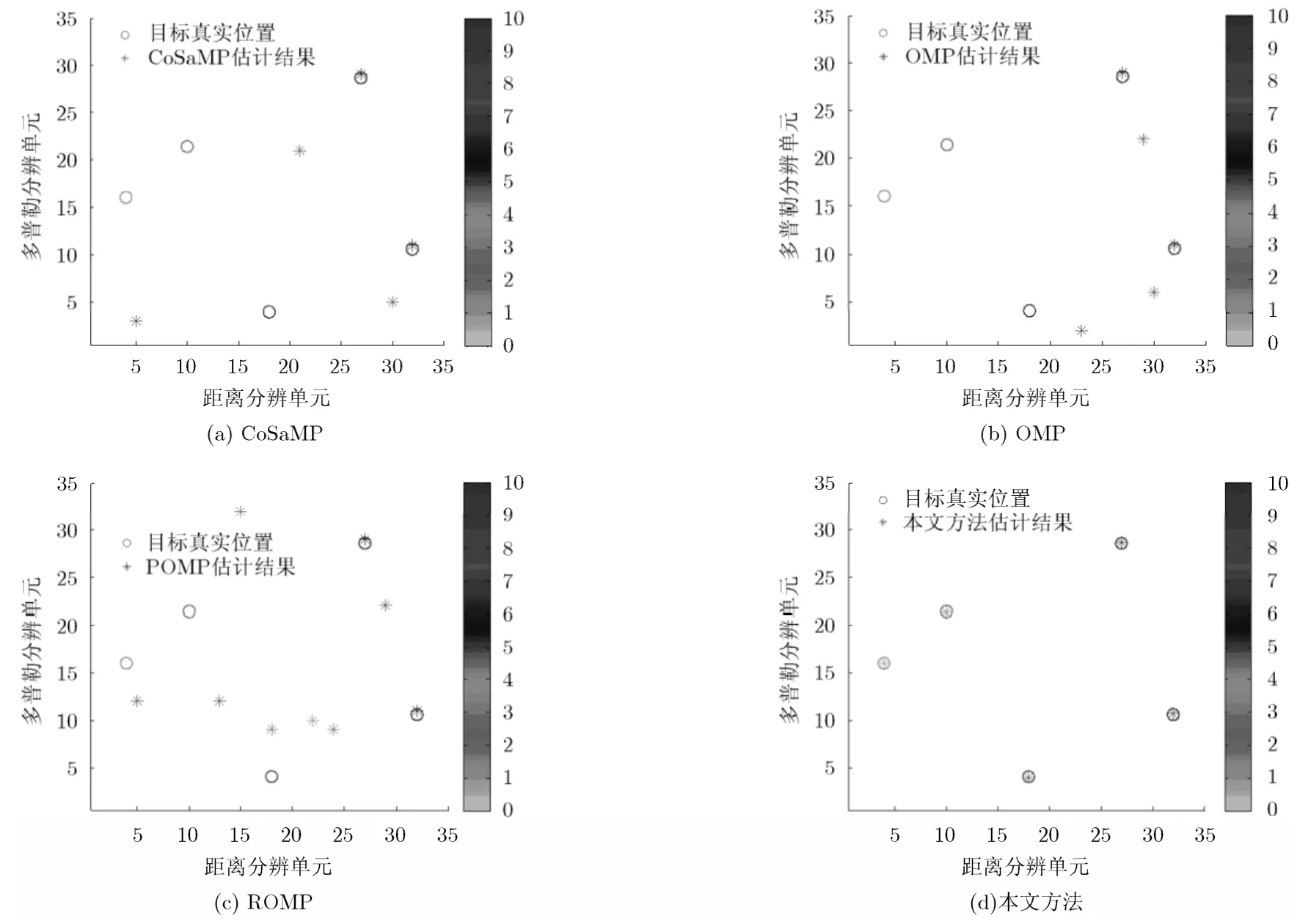
图1 各算法目标距离-多普勒成像输出结果对比

由图2可见，CoSaMP, OMP, ROMP等算法目标散射系数矢量估计误差较大，因为当系统预先设定的距离-多普勒分辨单元无法准确表示目标场景时，上述算法不具备系统模型失配误差的抑制能力，使得CSR对目标场景的适用性变差，导致对目标所在分辨单元位置的估计随信噪比的降低出错情况不断增加，严重影响了目标参数的估计精度。相比而言，本文方法迭代过程中以较高精度对系统模型失配误差进行了估计，并利用该结果逐步校正了CSR感兴趣区域中相关参数的量化结果，改善了感知矩阵和目标散射系数矢量的匹配关系；同时，通过波形优化方法保证了对应感知矩阵列之间的非相干性最优，提高了低信噪比条件下选取目标参数支撑集的准确性，故本文方法具有更高的目标散射系数估计精度，以及更好的稳健性。

实验 3 目标数量变化时目标散射系数估计RMSE分析。设CSR回波信噪比为SNR 6 dB= ，目标随机分布在CSR感兴趣区域内，其数量变化范围为[2,20]，其它参数设置同实验 1。图 4对比了CoSaMP, OMP, ROMP等算法与本文方法在目标数量不同时目标散射系数矢量估计均方根误差的500次蒙特卡洛实验结果。图5为目标数量不同时，本文方法对系统模型失配误差估计均方根误差的500蒙塔卡洛实验结果。

由图5可见，随着目标数量的增加，CoSaMP,OMP, ROMP等算法较本文方法对目标散射系数矢量的估计性能严重劣化。由于目标随机分布在感兴趣区域内，无法保证目标准确出现在CSR系统预先设定的距离-多普勒分辨单元网格上，使得随着目标数量的增加对应感知矩阵与目标散射系数矢量失配的概率不断上升，失配的程度不断加剧，然而上述算法不具备系统模型的校正能力，无法改善CSR系统模型对目标场景的适用性，导致目标信息估计误差随着目标数量的增加不断扩大；相比而言，虽然本文方法随目标数量的增加对应目标参数估计性能有所下降，但由于其在迭代过程中逐步对CSR系统模型进行校正和优化，使该模型对目标场景的适用性得到了改善，保证了本文方法目标参数估计的有效性和稳健性。

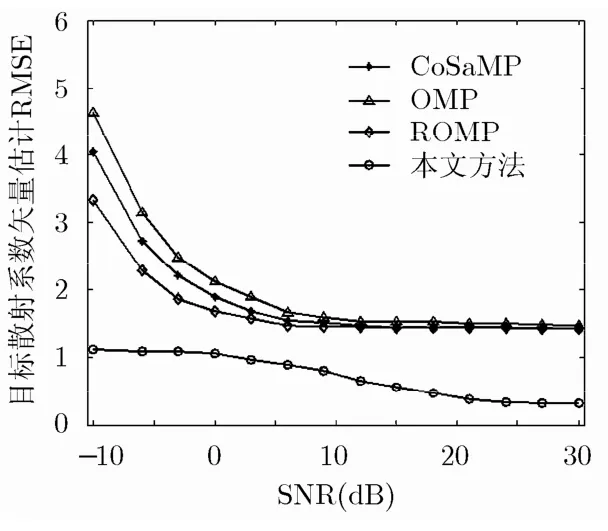
图2 不同信噪比时各算法目标散射系数估计RMSE曲线

图3 不同信噪比时感知矩阵 失配误差估计RMSE曲

图4 目标数量不同时各算法目标 散射系数估计RMSE曲线

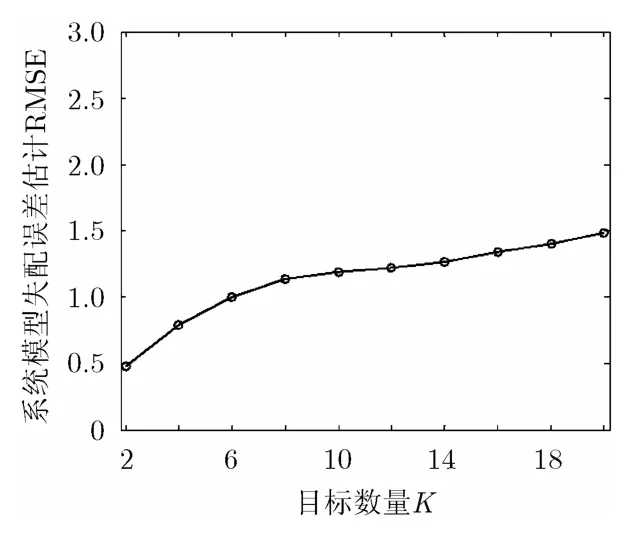
图5 目标数量不同时感知矩阵失配误差估计RMSE曲线

6 结论

通过校正和优化系统模型改善目标信息的估计性能是 CSR系统设计的一个重要方面，对于提高CSR在复杂工作环境中运行的有效性和稳健性有着重要的理论和实际意义。本文针对感知矩阵和目标信息矢量失配背景下距离-多普勒参数估计性能下降的问题，提出一种稳健的盲稀疏度CSR目标参数估计算法，显著降低了系统模型失配误差对CSR的影响。与传统CSR算法相比，本文方法改善了目标信息矢量估计性能，增强了CSR目标参数估计的稳健性和有效性。

[1] Li G, Zhu Z, Yang D, et al.. On projection matrix optimization for compressive sensing systems[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2887-2898.

[2] Julio M, Cuo S, Lawrence C, et al.. Task-driven adaptive statistical compressive sensing of Gaussian mixture models[J].IEEE Transactions on Signal Processing, 2013, 61(3):585-600.

[3] 武昕, 王岩飞, 刘畅. 基于压缩感知理论的随机噪声雷达目标检测算法研究[J]. 电子与信息学报, 2012, 34(7): 1609-1615.Wu Xin, Wang Yan-fei, and Liu Chang. A target detection algorithm based on compressive sensing for random noise radar[J]. Journal of Electronics ＆amp; Information Technology,2012, 34(7): 1609-1615.

[4] Julian W, Simon H, and Martin K. Analysis based blind compressive sensing[J]. IEEE Signal Processing Letters, 2013,20(5): 491-494.

[5] Miosso C, Borries R, and Pierluissi J. Compressive sensing with prior information requirements and probabilities of reconstruction in l1-minimization[J]. IEEE Transactions on Signal Processing, 2013, 61(9): 2150-2164.

[6] Tello A, Lopez D, and Mallorqui J. A novel strategy for radar imaging based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4285-4295.

[7] Matthew H and Thomas S. General deviants: an analysis of perturbations in compressed sensing[J]. IEEE Journal of Selected Topics in Signal Processing: Special Issue on Compressed Sensing, 2010, 4(2): 342-349.

[8] Liu Z, Wei X, and Li X. Aliasing-free moving target detection in random pulse repetition interval radar based on compressed sensing[J]. IEEE Sensor Journal, 2013, 13(7):2523-2534.

[9] Zhu H, Geert L, and Georgios G. Sparsity-cognizant total least-squares for perturbed compressive sampling[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2002-2016.

[10] Chen C and Vaidyanathan P. Compressed sensing in MIMO radar[C]. 2008 42nd Asilomar Conference on Signal, Systems and Computers, Piscataway, 2008: 41-44.

[11] Song X, Zhou S, and Willett P. The role of the ambiguity function in compressed sensing radar[C]. 2010 IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, 2010: 2758-2761.

[12] Chi Y, Louis S, Ali P, et al.. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2182-2195.

[13] Daniel C, Parastoo S, and Rodney K. Effects of basis-mismatch in compressive sampling of continuous sinusoidal signals[C]. Proceedings of the 2010 2nd International Conference on Future Computer and Communication, Canberra, 2010: 2739-2743.

[14] Gleichman S and Eldar Y. Blind compressed sensing[J]. IEEE Transactions on Information Theory, 2011, 57(10):6958-6975.

[15] Deng H. Synthesis of binary sequences with good autocorrelation and corsscorrelation properties by simulated annealing[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 98-107.

[16] Yao Y, Athina P, and Vincent P. Measurement matrix design for compressive sensing based MIMO radar[J]. IEEE Transactions on Signal Processing, 2011, 59(11): 5338-5352.

[17] Wu H and Wang S. Adaptive sparsity matching pursuit algorithm for sparse reconstruction[J]. IEEE Signal Processing Letters, 2012, 19(8): 471-474.