基于方位谱分析的斜视TOPS SAR子孔径成像方法

杨 军孙光才 吴玉峰 邢孟道

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

ScanSAR和TOPS SAR是实现宽测绘带的两种常见SAR成像模式。ScanSAR通过周期性地调整波束在俯仰维的指向来获得距离向宽测绘带，但是由于波束在方位维的不连续性使得图像在方位向存在明显的扇贝效应[1]。TOPS SAR通过在方位维的波束扫描来获得方位向宽测绘带，同时克服了ScanSAR模式存在的上述缺陷。由于 TOPS SAR的这些优点，该成像模式成为近几年的研究热点[26]-。2007年，TerraSAR-X系统进行了 TOPS SAR模式的数据录取并成功处理得到了聚焦图像及干涉结果[79]-，该模式也将成为Sentinel-1卫星的基本模式之一[10]。TOPS SAR由于波束指向的变化，导致扫描场景回波信号的方位带宽急剧增大，通常大于系统的脉冲重复频率，因此全孔径回波信号在方位频域是混叠的；另外在TOPS SAR模式下，扫描周期内场景的方位测绘带要远大于平台运行距离，因此距离徙动校正后的信号在方位时域是模糊的。上述问题都给TOPS SAR模式成像处理带来了困难。正侧视TOPS SAR模式只对雷达平台正侧方的区域进行扫描，限制了其应用前景。若雷达能工作在斜视模式，则可以实现更大范围的监视和快速重访，也可以提前发现目标，大大提高了雷达的灵活性和安全性，扩大了应用范围。斜视SAR特殊的成像几何特性决定了回波信号存在严重的距离徙动，这导致距离向和方位向的耦合严重。因此斜视TOPS SAR同时具有斜视模式距离向和方位向强耦合的特性及TOPS SAR方位模糊特性，这都增加了成像处理的难度。

从现有文献看，针对TOPS SAR成像方法的研究主要还集中于正侧视，归纳起来可以分为两类：子孔径成像方法及全孔径成像方法。在子孔径成像方法中，方位信号被分成多个子孔径信号，保证每个子孔径方位信号的带宽都小于系统脉冲重复频率，然后进行距离徙动校正及距离脉冲压缩，最后在方位时域拼接并进行聚焦处理[11]。全孔径算法首先进行方位向预处理，以获得无模糊的信号频谱，然后采用传统的 SAR成像算法进行距离徙动校正及距离脉冲压缩[1214]-。针对斜视TOPS SAR的成像算法研究较少，文献[15]中提出了一种全孔径的成像处理算法，通过方位预处理获得信号无模糊的 2维频谱；然后采用修正的线性变标算法进行距离徙动校正；最后在频域采用非线性变标算法及谱分析技术将目标聚焦在方位频域并进行几何形变校正。

本文提出一种斜视 TOPS SAR子孔径成像方法。首先对子测绘带回波数据进行子孔径划分并在时域适当进行扩展，获取子孔径回波信号无模糊的2维频谱后，采用修正的距离徙动算法对每个子孔径的数据进行距离徙动校正和距离脉冲压缩，最后在方位频域对子孔径信号进行拼接处理，获得全孔径信号无模糊的方位频谱，结合谱分析技术将信号聚焦在方位频域。相比文献[15]中的全孔径成像算法，本文提出的子孔径算法不需要进行几何形变校正，另外该算法中是以航向为坐标轴建立的直角坐标系，便于子测绘带图像拼接形成大场景图像。

2 斜视TOPS SAR成像几何及信号模型

图1所示为斜视TOPS SAR成像几何示意图，图中只画出了其中一个子测绘带。平台以速度v作匀速直线运动。O点为全孔径中心时刻雷达平台所处的位置，雷达与场景中心的距离为SR ，扫描周期的中间时刻波束中心斜视角为0θ。天线波束宽度为，子测绘带回波数据录取过程中雷达从M点运动到N点，相应的波束指向从1θ以旋转角速度ω匀速变化到2θ。以O点为坐标原点，雷达航向为横轴，建立如图1所示的直角坐标系，那么雷达的位置可以表示为，其中at为方位慢时间。由图1的几何关系可知，对于不同方位位置的点目标，其经历的波束扫描角度是不一样的，因此其方位频谱支撑区也是不一样的。图2为斜视TOPS SAR子测绘带中点目标方位信号的时频关系图，其中两条斜虚线的中间区域表示场景的时频分布区，粗实线为场景点目标的时频线。用iB表示瞬时带宽，脉冲重复频率PRF稍大于iB,aT为方位全孔径时间，aB为全孔径回波信号的方位带宽。从图2可以看出，点目标多普勒中心随方位位置变化，导致整个场景的方位带宽增加，因此子测绘带回波信号在方位频域是模糊的。对全孔径的数据进行适当分块，可以使子孔径数据在方位频域不模糊。

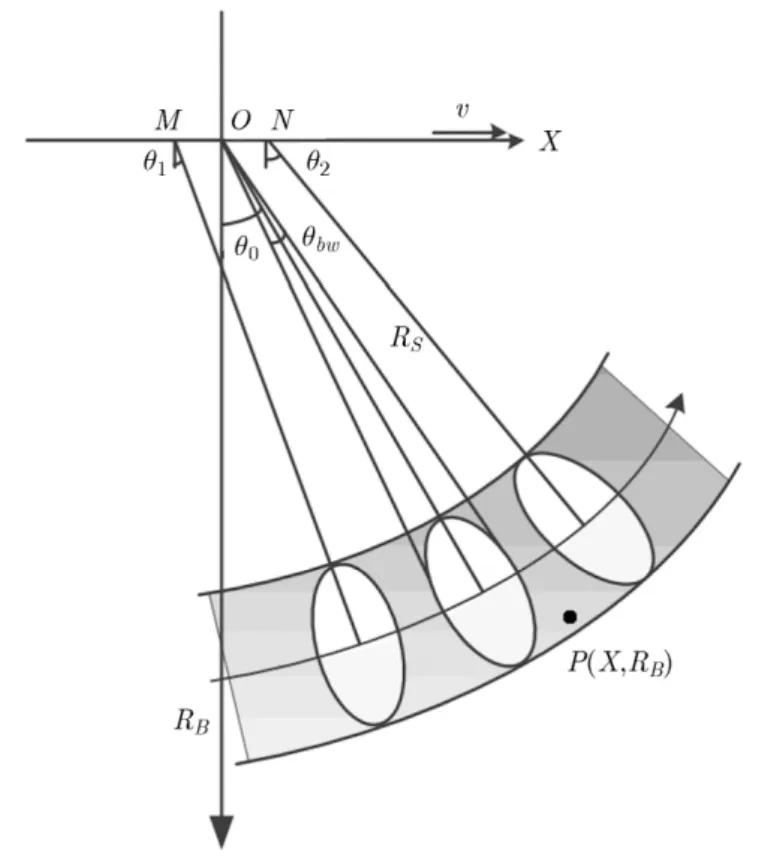
图1 斜视TOPS SAR成像几何示意图(单子测绘带)

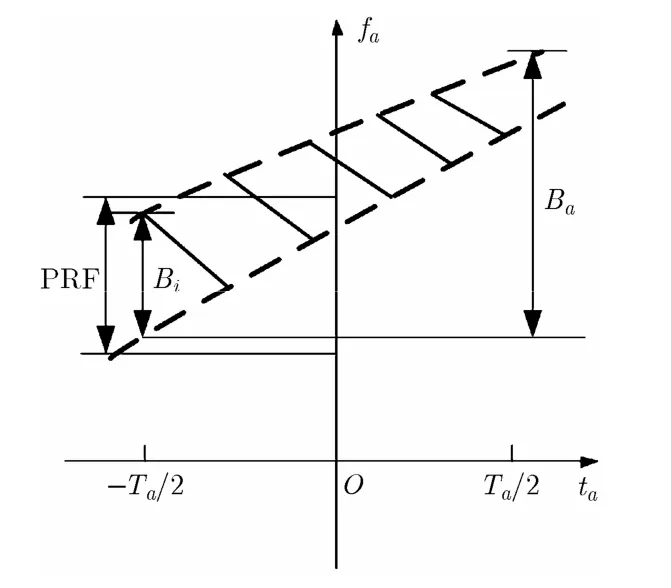
图2 斜视TOPS SAR点目标方位信号时频关系图

以子孔径中心时刻为坐标原点，以航向为X轴建立坐标系。对于子测绘带中的点目标，雷达发射线性调频信号，则其基带回波信号在距离频域可表示为

其中rf为距离频率，c为光速，γ为发射信号调频率，为雷达载频，为波束中心指向P点时的方位时刻。和分别表示线性调频信号的距离频域窗函数和方位时域窗函数，为瞬时斜距，可表示为

回波信号距离脉冲压缩后在2维波数域可以表示为

3 子孔径成像处理方法

本文讨论的斜视 TOPS SAR子孔径成像方法主要包括3个步骤：第1步是通过修正的RMA算法来实现距离徙动校正和距离脉冲压缩；第2步在方位频域实现子孔径数据的拼接获得全孔径信号无模糊的方位频谱；第3步结合SPECAN技术将点目标聚焦在方位频域。

3.1 距离徙动校正和距离脉冲压缩

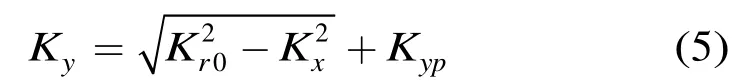
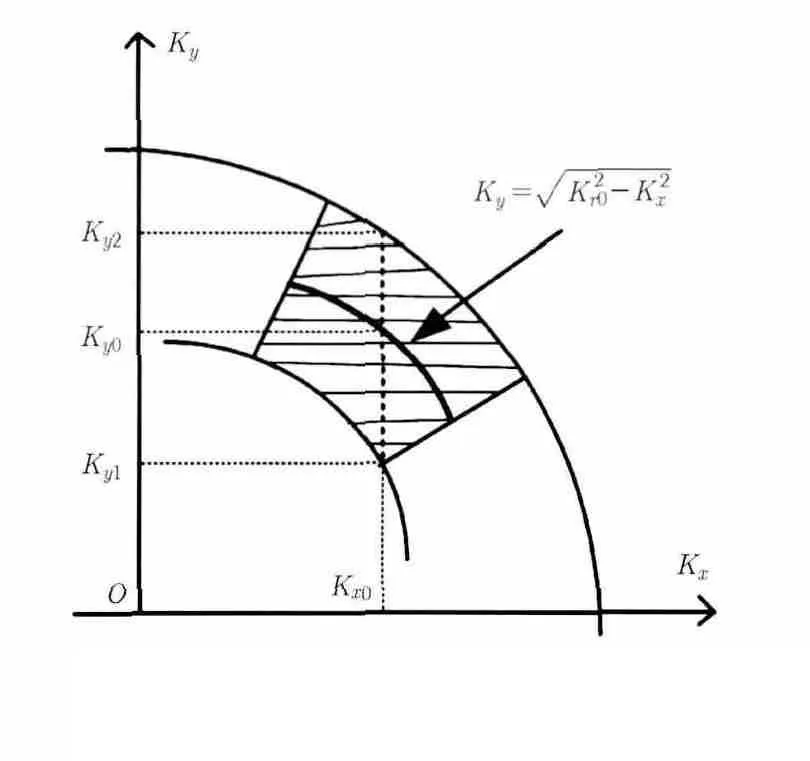
图3 斜视SAR的 K y - K x 2维波数谱

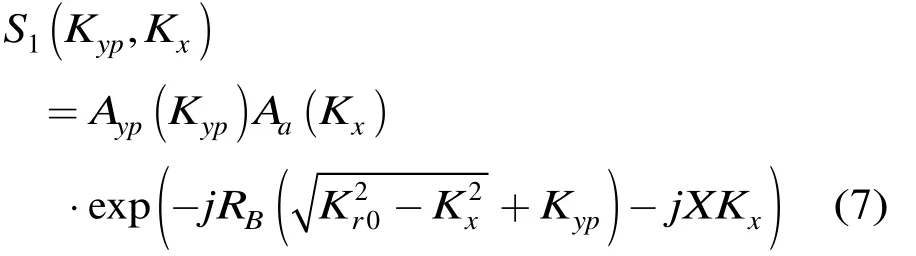
为了便于对方位信号进行分析，可以补偿式(8)中的双曲相位项，补偿函数及补偿后方位频域信号可以分别表示为

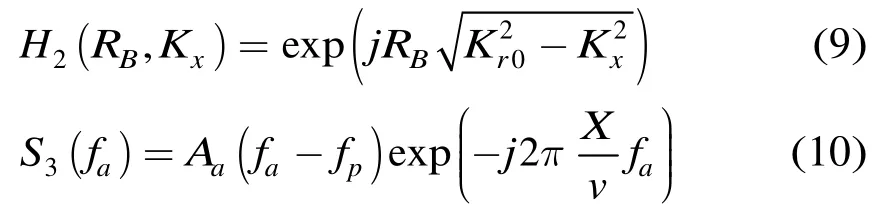
若根据子测绘带的方位幅宽将原始子孔径信号在时域进行扩展，可以使式(10)表示的方位信号在时域不混叠，直接进行逆傅里叶变换就可以实现点目标的聚焦。由于扫描场景的方位幅宽要远大于雷达平台运行距离，此时在时域扩展倍数太大，导致数据量急剧增加，增加了成像处理的时间。本文主要考虑如何在时域扩展倍数较小的情况下实现点目标方位聚焦。

3.2 子孔径数据拼接获取全孔径无模糊方位频谱

式(10)中表示的子孔径方位信号在时域是模糊的，但在频域是不模糊的。一次完整扫描周期中，波束中心斜视角逐渐增加，其对应的多普勒中心也逐渐增加，因此可以在方位频域进行子孔径数据拼接获取全孔径信号的方位频谱。

图4 点目标在不同坐标系中坐标转换示意图

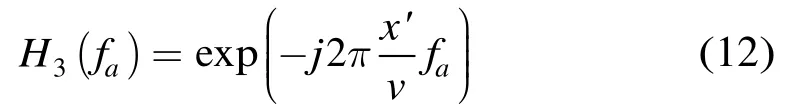
补偿后，各点目标的方位信号在不同坐标系中可以统一用式(10)表示，这样就可以在方位频域对各子孔径数据进行拼接，获取全孔径信号无模糊的方位频谱。

3.3 方位聚焦

图5为子测绘带点目标的方位信号时频关系变换示意图，粗实线表示的是各点目标的方位信号时频关系。图5中右边部分3个虚线框分别代表的是近距离单元、远距离单元及中心距离单元中各点目标用式(10)所示的方位信号时频关系。从图中可以看到场景方位幅宽对应时间远大于扫描周期，因此式(10)表示的全孔径方位信号在时域是模糊的，这增加了方位聚焦处理的难度。在获取全孔径信号的方位频谱后，本文采用SPECAN技术来实现点目标方位聚焦。

进行 SPECAN处理的核心是在时频平面内寻找合适的旋转曲线，然后在频域构造二次相位函数，对式(10)所示的方位信号在频域内进行调制，使调制后整个场景的方位信号时宽最小，且关于对称分布。下面讨论旋转曲线的具体获取方法。

旋转曲线在时频平面内可以表示为

或

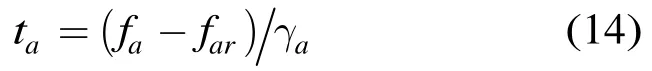
其中aγ为旋转曲线对应的调频率，为旋转曲线与轴的交点的频率坐标。旋转曲线的获取问题转换为参数及的求解问题。时频平面内的点用表示，本文中称为时频坐标点。在已知雷达工作参数情况下，可以计算得到各距离单元中点目标对应的时频坐标点，这些时频坐标点的集合可以用表示，集合中时频坐标点所描绘的图形的边沿点集合用表示，此时参数及的求解问题可以表示为

图5 子测绘带各距离单元点目标的方位信号时频关系变换示意图

式(10)所示方位信号与式(16)相乘，得到

式(17)所示方位信号在时域不再混叠，信号变换到方位时域可以写为

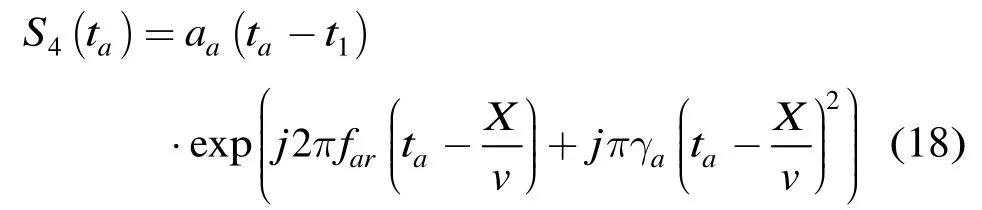
此时各点目标的时频关系有所变化，如图5中标①的箭头所示，由竖直线变为斜线。然后利用方位去斜(Deramp)操作补偿式(18)中的二次项，将点目标聚焦在方位频域。去斜曲线如图5所示，其在时频平面内可以表示为

将式(18)与式(20)相乘，并将结果变换到方位频域，可以得到

其中pB为点目标的方位信号带宽，此时信号聚焦在方位频域，点目标的时频关系变换图如图5中标②的箭头所示，由斜线变换到水平线。为了使算法具有保相性，利用构造相位补偿函数

可以得到最终成像结果。若方位分辨率和距离分辨率相差较大时，可以做多视处理。

4 成像算法流程

斜视 TOPS SAR子孔径成像算法流程如图 6所示。算法主要由4部分组成：首先由雷达工作参数计算等相关参数，并对子测绘带回波数据进行分块，若大于子孔径时宽，需要将子孔径数据在方位时域进行适当扩展；对传统RMA算法进行修正，在距离波数域进行sinc插值完成距离徙动校正，并补偿与距离相关的双曲相位项，简化方位信号处理难度；对子孔径数据进行线性相位补偿，在方位频域进行子孔径拼接获取全孔径无模糊的方位频域信号；然后在方位频域采用谱分析技术和方位去斜技术将点目标聚焦在方位频域；若方位分辨率和距离分辨率相差较大时，需要进行多视处理。

5 仿真实验

为了验证本文提出的斜视 TOPS SAR子孔径成像方法，本节给出了仿真试验结果。仿真参数见表1，仿真场景为9×11的矩形点阵，均匀分布在[12 km~20 km]×[8 km~15 km] (沿航向×垂直航向)的范围内，在图1建立的直角坐标系中的点目标位置如图7所示。对于斜视TOPS模式，只有部分点目标在子测绘带内，图中实线框大致标示了成像子测绘带。

通过对表1参数的计算可知，方位带宽为6012 Hz，远大于PRF，子测绘带全孔径方位信号在频域是模糊的。通过在方位维将原始数据适当分块，使得子孔径数据在方位频域不模糊。子孔径数据通过修正的RMA算法进行距离徙动校正和距离脉冲压缩后，在方位频域进行拼接，拼接结果如图 8所示，从图中可以看到，各点目标的距离徙动得到良好校正。由雷达的工作参数，可以计算得到。实际操作时，将子孔径数据扩展到了4 s。采用本文方法的成像结果如图9所示。图中水平方向为方位向，垂直方向为距离向，图像上端表示场景近端。图9(a)为成像结果，图9(b), 9(c), 9(d)分别对应子测绘带中A, B, C 3点的等高线图。表2给出了上述3点的成像性能分析结果，其中PSLR为峰值旁瓣比，ISLR为积分旁瓣比，可见点目标均得到了良好的聚焦，成像效果较为理想。从成像结果可以看出，A, B, C 3点的方位分辨率依次降低，这是由于随着扫描角度的增大，3点对应的方位带宽依次减小所致。

表1 仿真参数

图6 斜视TOPS SAR子孔径成像算法流程

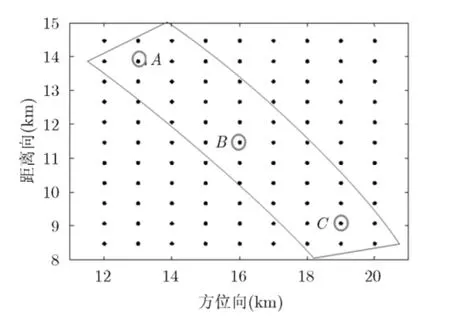
图7 仿真场景点目标分布

图8 距离脉冲压缩后全孔径方位频域信号

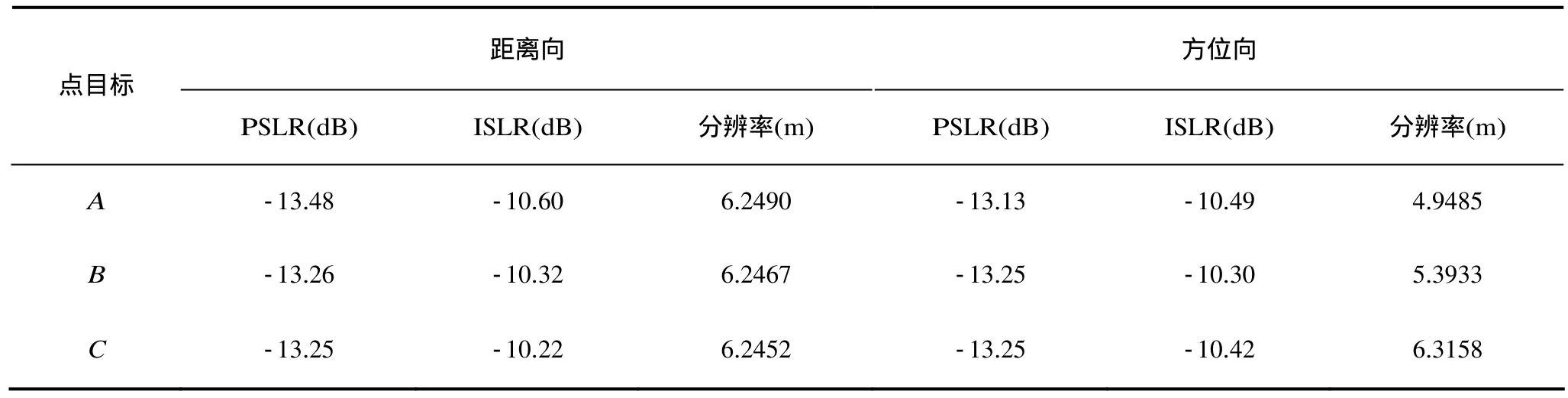
表2 成像性能分析

图9 仿真实验成像结果

6 结论

斜视 TOPS SAR由于同时存在距离向与方位向的强耦合性及方位频谱模糊问题，给成像带来了困难。本文提出了一种子孔径斜视TOPS SAR成像处理算法。对全孔径数据进行适当分块并在时域进行适当扩展，获得子孔径信号无模糊的2维频谱；然后在2维波数域采用修正的RMA算法完成距离徙动校正和距离脉冲压缩，并在方位频域进行子孔径拼接获取全孔径信号无模糊的方位频谱；此时全孔径信号在方位时域是模糊的，通过采用谱分析技术将点目标聚焦在方位频域。本文方法聚焦得到的图像不存在方位形变，不需要进行几何形变校正，另外本文中是以航向为坐标轴建立直角坐标系，利于大场景图像的拼接。仿真实验结果验证了本文方法的可行性。

[1] 徐伟, 邓云凯. 基于二维Chirp-Z变换的星载TOPSAR成像算法[J]. 电子与信息学报, 2011, 33(11): 2679-2685.Xu Wei and Deng Yun-kai. Imaging algorithm of spaceborne TOPSAR data based on two-dimension Chirp-Z transform[J].Journal of Electronics ＆amp; Information Technology, 2011,33(11): 2679-2685.

[2] Francesco D and Andrea M. TOPSAR: terrain observation by progressive scans[J]. IEEE Transactions on Geoscience Remote Sensing, 2006, 44(9): 2352-2360.

[3] Wollstadt S, Prats P, Bachmann M, et al.. Scalloping correction in TOPS imaging mode SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 614-618.[4] Xu Wei, Deng Yun-kai, Feng Fan, et al.. TOPS mode raw data generation from wide-beam SAR imaging modes[J].IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):720-724.

[5] Prats P, Scheiber R, Marotti L, et al.. TOPS interferometry with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3179-3188.

[6] Rodon J R, Broquetas A, Arbesú J M G, et al..Signal-to-noise ratio equalization for TOPSAR mode using a nonuniform steering rate[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 199-203.

[7] Meta A, Prats P, Steinbrecher U, et al.. First TOPSAR image and interferometry results with TerraSAR-X[C]. Proceedings of Fringe Workshop, Frascati, Italy, 2007: 1-8.

[8] Meta A, Mittermayer J, Prats P, et al.. TOPS imaging with TerraSAR-X: mode design and performance analysis[J]. IEEE Transactions on Geoscience Remote Sensing, 2010, 48(2):759-769.

[9] Marotti L, Prats P, Scheiber R, et al.. Differential SAR interferometry with TerraSAR-X TOPS data: Mexico City subsidence results[C]. EUSAR 2012, Nuremberg, Germany,2012: 677-680.

[10] Evert A, Malcolm D, Nicolas F, et al.. Sentinel-1 ESA’s new European radar observatory[C]. EUSAR 2008,Friedrichshafen, Germany, 2008: 179-182.

[11] Prats P, Scheiber R, Mittermayer J, et al.. Processing of sliding spotlight and TOPS SAR data using baseband azimuth scaling[J]. IEEE Transactions on Geoscience Remote Sensing, 2010, 48(2): 770-780.

[12] Sun Guang-cai, Xing Meng-dao, Wang Yong, et al.. Sliding spotlight and TOPS SAR data processing without subaperture[J]. IEEE Geoscience and Remote Sensing Letters,2011, 8(6): 1036-1040.

[13] Engen G and Larsen Y. Efficient full aperture processing of TOPS mode data using the moving band chirp z-transform[J]. IEEE Transactions on Geoscience and Remote Sensing,2011, 49(10): 3688-3693.

[14] Xu Wei, Huang Ping-ping, Deng Yun-kai, et al.. An efficient approach with scaling factors for TOPS-mode SAR data focusing[J]. IEEE Geoscience and Remote Sensing Letters,2011, 8(5): 929-933.

[15] 杨军, 吴玉峰, 孙光才, 等. 基于方位 FNCS的斜视 TOPS SAR成像方法[J]. 系统工程与电子技术, 2012, 34(11): 86-92.Yang Jun, Wu Yu-feng, Sun Guang-cai, et al.. Squint TOPS SAR imaging method based on azimuth FNCS[J]. Systems Engineering and Electronics, 2012, 34(11): 86-92.