Alpha稳定分布噪声下时频重叠信号的载波频率估计方法

李兵兵 马洪帅 刘明骞

(西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安 710071)

1 引言

随着通信技术的发展，电磁环境变得日益复杂，通信领域中的时频重叠信号越来越多，如相邻卫星靠得过近会形成邻星信号干扰，信号日益密集会造成同频信号重叠，这类信号一方面极大地影响了系统的接收性能，另一方面导致传统的单信号处理方法不再适应，因此迫切需要研究有效的处理方法。时频重叠信号的载波频率估计是时频重叠信号处理中的重要一环，既可以作为盲分离算法初始值设置的依据，又可以预估盲分离效果。传统时频重叠信号的载波频率估计是假设背景噪声服从高斯分布，但在实际的无线通信系统中往往存在一些非高斯分布的噪声，这些噪声具有显著尖峰脉冲状波形和较厚概率密度函数拖尾。文献[1-3]在充分研究各种随机过程模型后，发现Alpha稳定分布模型是描述这类随机信号的一种更有效的噪声模型。因此，研究在Alpha稳定分布噪声下时频重叠信号的载波频率估计方法具有实际的工程意义。

目前，针对时频重叠信号的载波频率估计方法研究较少，文献[4]提出一种基于四阶循环累积量的时频重叠信号载波频率估计方法，但是该方法受重叠信号分量的类型及个数的限制。文献[5]利用循环谱包络对未经成形滤波的双BPSK重叠信号的载波频率进行了估计，但是该方法受重叠信号分量的类型及成形滤波的影响较大。文献[6]提出了一种利用能量中心的频谱细化方法估计重叠信号的载波频率，但是该方法在低信噪比条件下载频估计精度较差，且限定了信号分量的调制类型而缺乏普适性。此外，上述载波频率估计方法仅适用于高斯噪声环境，而在Alpha稳定分布噪声下均失效。

针对以上问题，本文提出一种基于广义四阶循环累积量的时频重叠信号载波频率估计方法，该方法利用广义四阶循环累积量的幅度谱的循环频率与重叠信号的载波频率相对应以及循环频率处存在离散谱线的特性，通过检测离散谱线的位置所对应的循环频率估计出重叠信号各个信号分量的载波频率。仿真结果表明，当混合信噪比大于等于0 dB时，该载波频率估计方法具有良好的性能。可见，在Alpha稳定分布噪声下，该估计方法是有效可行的。

2 信号和噪声模型

Alpha稳定分布噪声下时频重叠信号的模型表示为

表示信号分量的相位， ()n t为加性的标准Alpha稳定分布噪声。

Alpha稳定分布是唯一能满足广义中心极限定理的分布，因Alpha稳定分布不具备统一闭式的概率密度函数，通常情况下用特征函数对其进行描述[79]-：

3 时频重叠信号的载波频率估计方法

3.1 广义四阶循环累积量

四阶循环累积量是利用信号的循环平稳特性进行信号参数估计的一种有效方法，但当噪声模型为Alpha稳定分布时，由于其不具有α阶及以上各阶统计量[10]而失效，则对应的参数估计方法也将失效。由于Alpha稳定噪声不存在二阶及二阶以上的统计量，为了对Alpha稳定噪声进行处理，使其具有平稳遍历特性和有限值的二阶矩以及四阶矩，因此本文提出广义循环矩和广义四阶循环累积量的概念，具体定义如下：

定义1 广义循环矩

定义2 广义四阶循环累积量

定义2中的广义四阶循环累积量和传统的四阶循环统计量具有相同的循环频率[11]。

结合定义1和定义2，式(4)可表达为

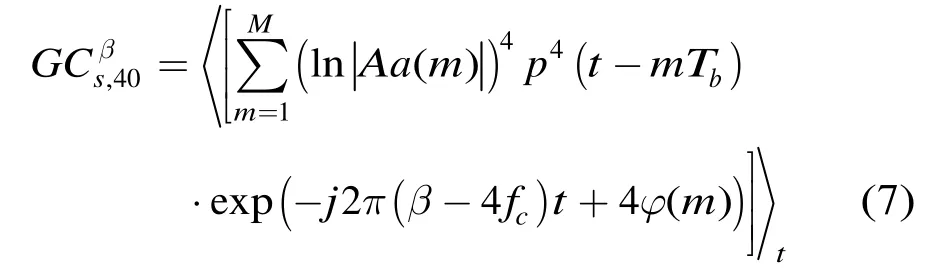
3.2 载波频率估计方法

针对QPSK, 16QAM, 64QAM任意两两组合的重叠信号，其广义四阶循环累积量的幅度谱为

离散谱线的检测方法具体描述如下[12]：假设表示接收重叠信号的广义四阶循环累积量的幅度谱，0f表示出现最大值的频点，用与平均值的比值表示0f处幅度谱的突出程度，并且当该比值大于某一阈值δ时认为0f位置出现离散谱线。由于频率分辨率的原因，广义四阶循环累积量幅度谱上显示的离散谱线通常不是一根而是靠在一起的多根谱线的集合，为了抑制这些谱线对下次求最大值的影响，需要在判决后将在0f附近一个小区间内的谱线值置零，其中。

综上所述，本文提出的Alpha稳定分布噪声下时频重叠信号的载波频率估计方法的具体步骤如下：

步骤 2 根据上述的离散谱线检测方法，检测出最高离散谱线，将其所在的位置记为1P，并将其邻域区间的谱线值置零；

步骤 3 当重叠信号的k个信号分量的载波频率各不相同时，重复步骤2，并根据信号分量个数k依次可得到，则这些位置所对应的循环频率值即为各个信号分量的载波频率值。

4 载波频率估计方法的渐近性分析

本文的载波频率估计是针对标准Alpha稳定分布噪声环境下的时频重叠信号，噪声以及各个信号分量间是彼此相互独立的。在此以时频重叠双信号为例分析本文载频估计方法的渐近性。

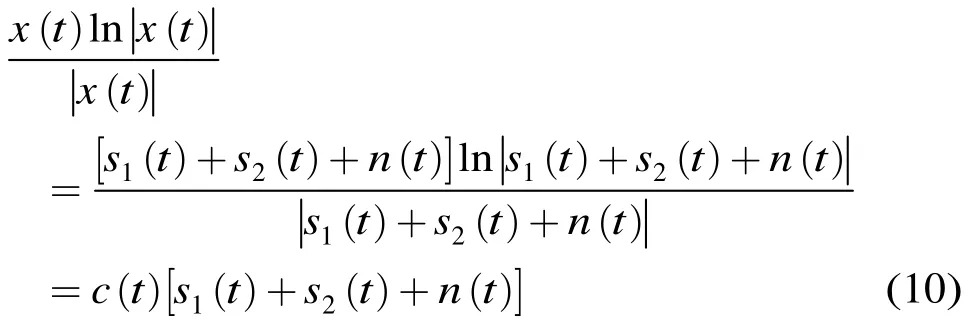
结合定义1和定义2，对式(4)中的广义四阶循环矩部分的分析如下：

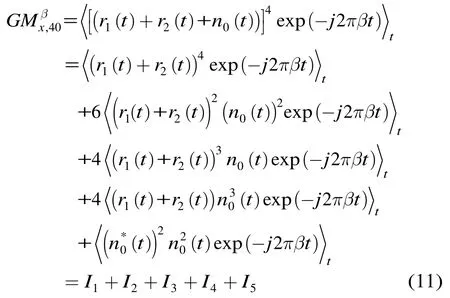
其中1I为信号项，5I为噪声项。

对于信号项1I的分析如下：

结合定义1和定义2，对式(4)中的广义二阶循环矩部分的分析如下：

其中7L为多项交叉项，由文献[14]可知的速率消失，同理可得和均以的速率消失。由于7L中项较多，在此仅以其中一项为例进行说明：的循环频率不同，而且在其非循环频率处的值为0，则以的速率消失，同理分析可知以的速率消失。

结合以上分析，式(4)可表示如下：

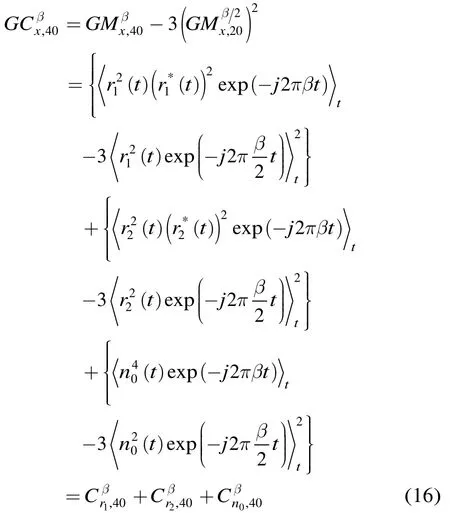
对于式(16)中的噪声项分析如下，Alpha稳定分布噪声的主要表现是短时大幅度脉冲，这也是Alpha稳定分布噪声对有用信号的主要干扰，此时，由此可以作如式(17)的近似：

由文献[15, 16]可知，非线性变换后的Alpha稳定分布噪声具有有限值的四阶矩和二阶矩，并且该噪声为平稳遍历过程，可具体表示为

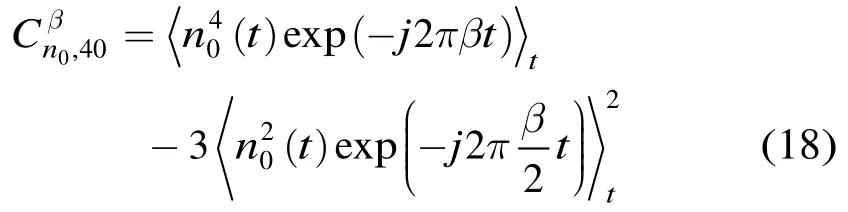
5 仿真结果及分析

为了验证本文估计方法的有效性，进行MATLAB仿真实验。本文采用时频重叠信号模型，噪声为加性标准S Sα分布噪声，其中混合信噪比定义为[11]

实验 1 为了测试混合信噪比对时频重叠信号载波频率估计性能的影响，对 QPSK, 16QAM,64QAM 信号任意两两组合的重叠情况进行仿真，Alpha稳定噪声的特征指数设为1.5。任意两个信号的参数设置如下：载波频率为=2.7 kHz与，码元速率为=1.2 kBaud与=1.6 kBaud，采样频率=19.2 kHz，数据长度为25600，信号分量功率比分别为1:1，其仿真结果如图1所示。

从图1中可以看出，对于双信号重叠的情况，当混合信噪比大于等于0 dB时，载波频率的估计正确率可达到98%以上。由此可以说明，本文所提出的时频重叠信号的载波频率估计方法是有效可行的。

实验 2 为了测试时频重叠信号分量的功率比对载波频率估计性能的影响，对QPSK, 16QAM，64QAM信号的任意两两组合，其中任意两个信号的参数设置如下：载波频率为=3.1 kHz与=3.3 kHz，码元速率为=1.2 kBaud与=1.6 kBaud，即频谱重叠率为100%，采样频率=19.2 kHz，数据长度为25600，信号分量功率比分别为1:1.5，其仿真结果如图2所示。

通过图1和图2可以看出，当信号分量的功率差别逐渐增大时，载波频率估计性能有所下降，这是因为信号分量功率差别的增大会引起信号分量的广义四阶循环累积量的差别增大。由此可以说明，信号分量的功率比也是影响本文方法估计性能的关键因素之一。

实验 3 为了测试频谱重叠率对时频重叠信号载波频率估计的影响，对QPSK, 16QAM, 64QAM信号任意两两组合的重叠情况，Alpha稳定噪声的特征指数为1.5，混合信噪比为0 dB。任意两个信号的参数设置如下：码元速率为=1.2 kBaud与，采样频率，数据长度=3.3 kHz组合，为25600，载波频率为=1.9 kHz与=2.2 kHz与=3.3 kHz组合，=2.5 kHz与=3.3 kHz组合，=2.8 kHz与=3.3 kHz组合，=3.1 kHz与=3.3 kHz组合，则对应的频谱重叠率分别为0%, 25%, 50%, 75%, 100%，其仿真结果如图3所示。

从图3中可以看出，随着频谱重叠率的增加，本文方法的估计正确率略有下降，但是其性能下降不大，在频谱重叠率为100%时，重叠双信号的载波频率估计正确率均在 93.4%以上，由此可以说明本文方法对频谱重叠率具有良好的稳健性。

实验4 为了对比本文方法与传统的基于四阶循环累积量的时频重叠信号载波频率估计性能，其中信噪比定义为：为重叠信号的功率，N为高斯白噪声功率。对 QPSK, 16QAM,64QAM信号的任意两两组合，其中任意两个信号的参数设置如下：载波频率为=2.7 kHz与=3.3 kHz，码元速率为=1.2 kBaud与=1.6 kBaud，采样频率=19.2 kHz，数据长度为25600，其仿真结果如图4所示。

从图4中可以看出，当加载的噪声为高斯噪声时，本文方法与传统的基于四阶循环累积量的估计方法的性能相当。传统的基于四阶循环累积量的估计方法需要进行次复数乘法和次复数加法，而本文方法的计算复杂度与其为同一数量级，仅多需要进行2N次复数乘法。由此可以说明，本文方法也可以适用于高斯环境。

图1 不同混合信噪比下重叠双信号的载波频率估计性能

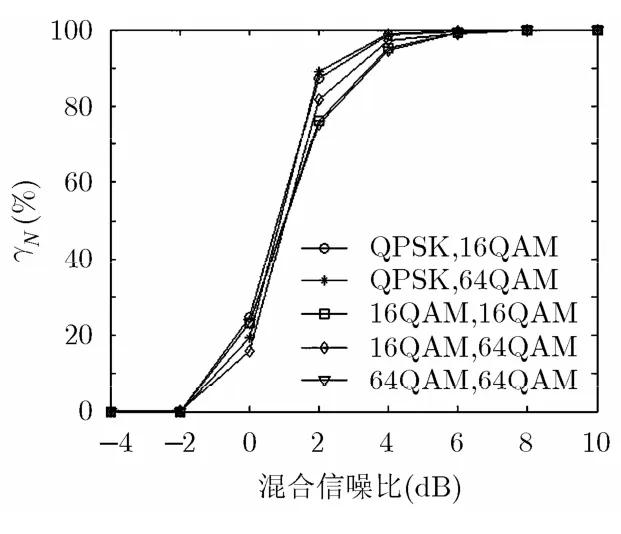
图2 分量功率比为1:1.5时 载波频率的估计性能

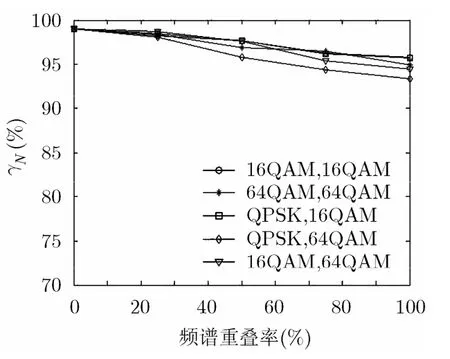
图3 不同频谱重叠率下重叠双 信号的载波频率估计性能

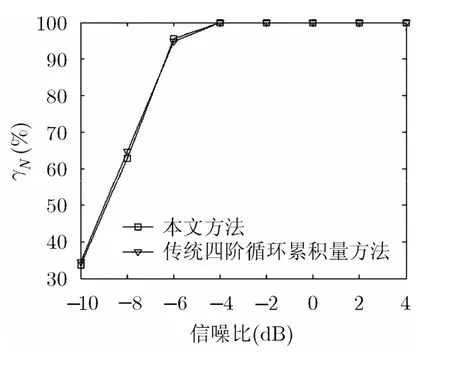
图4 高斯噪声下重叠信号的载波频率估计性能的对比

6 结束语

在Alpha稳定分布噪声情况下，本文提出了一种基于广义四阶循环累积量的时频重叠信号载波频率估计方法。该方法提出了时频重叠信号广义四阶循环累积量的定义，然后利用广义四阶循环累积量幅度谱的循环频率与重叠信号的载波频率相对应以及循环频率处存在离散谱线的特性估计出重叠信号的载波频率，并通过理论分析说明了该估计方法是渐近无偏和一致的。仿真结果表明，该方法不仅在考虑滚降滤波以及不同频谱重叠率的情况下具有良好的估计性能，而且在噪声特征指数变化的情况下该方法也均有较高的估计正确率。由此说明，在Alpha稳定分布噪声下，该方法具有良好的稳健性。

[1] Chavali V G , Da S, and Claudio R. Detection of digital amplitude-phase modulated signals in symmetric alpha-stable noise[J]. IEEE Transactions on Communications,2012, 60(11): 3365-3375.

[2] Mahmood A, Chitre M, and Armand M A. PSK communication with pass-band additive symmetric alpha-stable noise[J]. IEEE Transactions on Communications,2012, 60(10): 2990-3000.

[3] 刘晔, 黄芝平, 刘纯武. Alpha稳定分布混响建模及信号检测[J]. 国防科技大学学报, 2012, 34(4): 148-152.Liu Ye, Huang Zhi-ping, and Liu Chun-wu. Reverberation modeling and signal detection based on alpha stable distribution[J]. Journal of National University of Defense Technology, 2012, 34(4): 148-152.

[4] 王青红, 彭华, 王彬, 等. 基于循环累积量的共信道多信号检测和信号源个数估计算法[J]. 信息工程大学学报, 2012, 13(2):184-188.Wang Qing-hong, Peng Hua, Wang Bin, et al.. Detection and source estimation algorithm for co-channel multi-signals based on cyclic cumulants[J]. Journal of Information Engineering University, 2012, 13(2): 184-188.

[5] 于宁宇, 马红光, 石荣, 等. 基于循环谱包络的共信道多信号参数估计[J]. 西南交通大学学报, 2011, 64(6): 904-909.Yu Ning-yu, Ma Hong-guang, Shi Rong, et al.. Parameter estimation of co-channel multi-signals based on cyclic spectrum amplitude[J]. Journal of Southwest Jiaotong University, 2011, 64(6): 904-909.

[6] 朱波. 基于小波的单通道时频重叠信号参数分析与实现研究[D]. [硕士论文], 电子科技大学, 2011.Zhu Bo. Wavelet-based analysis and implementation of parameters for co-channel time-frequency overlapped signals[D]. [Master dissertation], University of Electronic Science and Technology of China, 2011.

[7] 刘明骞, 李兵兵, 曹超凤. 非高斯噪声下数字调制信号识别方法[J]. 电子与信息学报, 2013, 35(1): 85-91.Liu Ming-qian, Li Bing-bing, and Cao Chao-feng.Recognition method of digital modulation signals in non-gauss noise[J]. Journal of Electronics ＆amp; Information Technology, 2013, 35(1): 85-91.

[8] 王亢，徐志江，孟利民. 对称alpha 稳定分布的两段曲线逼近算法[J]. 通信学报, 2013, 34(1): 178-184.Wang Kang, Xu Zhi-jiang, and Meng Li-min. Approximation algorithm to symmetric alpha stable distribution with bi-region curve model[J]. Journal on Communications, 2013,34(1): 178-184.

[9] Xu Zhi-jiang, Wang Kang, and Wu Yuan. Minimumerror-based approximation model for symmetric alpha stable distribution[J]. Circuits, Systems ＆amp; Signal Processing, 2012,31(6): 2195-2204.

[10] Ángel N V and Jerónimo A G. Combination of recursive least-norm algorithms for robust adaptive filtering in alpha-stable noise[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1478-1482.

[11] 赵春晖, 杨伟超, 马爽. 基于广义二阶循环统计量的通信信号调制识别研究[J]. 通信学报, 2011, 32(1): 144-150.Zhao Chun-hui, Yang Wei-chao, and Ma Shuang. Research on communication signal modulation recognition based on the generalized second-order cyclic statistics[J]. Journal on Communications, 2011, 32(1): 144-150.

[12] 万坚, 涂世龙, 廖灿辉, 等. 通信混合信号盲分离理论与技术[M]. 北京: 国防工业出版社, 2012: 151-154.Wan Jian, Tu Shi-long, Liao Can-hui, et al.. Theory and Technology on Blind Source Separation of Communication Signals[M]. Beijing: National Defence Industry Press, 2012:151-154.

[13] Szabó Z, Póczos B, and Lrincz A. Separation theorem for independent subspace analysis and its consequences[J].Pattern Recognition, 2012, 45(4): 1782-1791.

[14] 于宏毅, 保铮. 平稳过程循环相关处理的有限数据消失特性[J]. 西安电子科技大学学报, 1999, 26(2): 133-136.Yu Hong-yi and Bao Zheng. Vanishing characteristics of stationary processes processed by cyclic correlation[J].Journal of Xidian University, 1999, 26(2): 133-136.

[15] Ma Xin-yu and Nikias C L. Parameter estimation and blind channel identification in impulsive signal environments[J].IEEE Transactions on Signal Processing, 1995, 43(12):2884-2897.

[16] Li Hua-liang, Li Xi-lin, Matthew A, et al.. A class of adaptive algorithms based on entropy estimation achieving CRLB for linear non-gaussian filtering[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 2049-2055.