基于应变速率循环法的TA15钛合金超塑性本构方程

谭丽琴， 王高潮， 甘雯晴， 熊 城

(南昌航空大学 航空制造工程学院，南昌330063)

在热变形过程中，材料本构方程反映了材料的流变应力与变形温度、应变速率和应变等热力学参数之间的依赖关系，在先进的塑性成形理论与技术研究发展中发挥着不可替代的作用。先进钛合金因具有密度低、比强度高、耐蚀性好等优良性能在航空工业领域获得广泛使用。先进钛合金的大量使用是新一代飞机和新型发动机先进性的显著标志之一［1］。TA15 钛合金因具有良好的热稳定性和焊接性能以及较好的工艺塑性而在航空领域得以应用［2］。合金主要应用于飞机结构件及发动机上，还能用来制造飞机隔框、壁板等工作温度较高、受力较复杂的重要结构件。近几年国内外对于钛合金超塑性的研究主要集中在α +β 两相区钛合金上［3，4］，对α 和近α 型钛合金的研究较少。目前，一些学者对该合金热变形行为的组织和性能进行了初步研究［5，6］，但是对热变形本构方程的研究较少。如何建立适用TA15 钛合金热变形的本构方程也是材料塑性成形前沿领域迫切需要研究解决的重要课题。

一般情况下，求解TA15 钛合金本构方程需要不同温度、不同应变速率下的组合实验［7～16］，而应变速率循环法通过一次拉伸试验便可获得完整的实验数据，跨越了应变速率区域的几个数量级。与普通方法相比，应变速率循环法能更高效，更快捷地构建超塑性本构方程。本工作采用应变速率循环法构建TA15 钛合金的超塑性本构关系，进行误差分析，运用国产1stopt 软件进行二元非线性回归，修正本构方程，保证其具有足够的精度，为TA15 钛合金超塑成形工艺过程的数值模拟提供了基础数据。

1 实验材料与方法

实验材料为TA15 钛合金，合金名义成分为Ti-6Al-2Zr-1Mo-1V，相变点在980 ～990℃之间，TA15钛合金由北京航空材料研究院提供，原始组织中初生α 相呈长条状，数量相对较多，β 相相对较少，平均晶粒尺寸约为25μm，见图1。

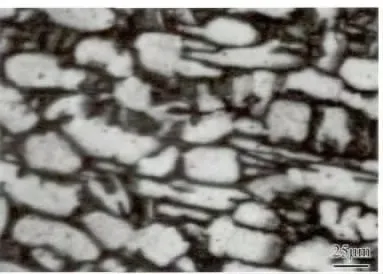
图1 TA15 原始试样显微组织Fig.1 Origin sample microstructure of TA15

应变速率循环法是使应变速率在一定范围内以一定规律往复循环变化进行拉伸试验的方法［3］。在开始阶段以初速率V0，时间T0进行初运行，以保证应变速率循环在塑性变形阶段进行，初运行结束后以最大应变速率开始运行，每隔相等的时间间隔，以Δ减小，运行半周期至最小应变速率，到达最小应变速率后，每隔相等的时间间隔，又以Δ增大，运行半周期至最大应变速率，就这样往复循环进行试验直到试样拉断。

参数设置，初始速率V0为0.8mm/min，初始运行位移为0.05mm，时间间隔为2s，循环半周期时间为5min，分别在850℃，900℃，950℃条件下，5 ×10－6～5 ×10－4s－1的应变速率范围内进行应变速率循环法超塑性拉伸试验。

2 结果与分析

2.1 应变速率循环法拉伸试验结果与分析

应变速率循环法超塑拉伸试验结果如图2 所示。在850℃时，伸长率达到614%，在950℃时，伸长率达到158%，在900℃时，合金的超塑性最佳，伸长率达到846%。

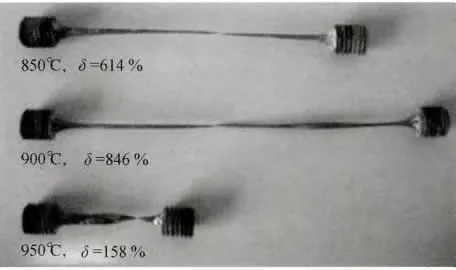
图2 超塑拉伸试验结果Fig.2 The samples before and after superplastic tensile test

图3 为应力与时间的关系曲线，可以看出:随着变形温度的升高，材料的流动应力逐渐降低，并且在不同的温度范围内表现出不同的流动特性，在850℃时，应变速率的变化导致流动应力变化最为剧烈，因为温度过低会导致材料变形难，变形需要更大的应力，而且软化机制的作用也不大。而在950℃时，应变速率的变化导致流动应力变化则较为平缓，这是因为随着变形温度的升高，材料的热激活作用增强，原子平均动能增大，晶体产生滑移的临界分切应力减小，从而减小了对材料位错运动和晶面间滑移的阻碍，并且，随着温度的升高，动态回复和动态再结晶也更容易进行，使得位错密度下降，抵消了塑性变形造成的加工硬化，促使材料流变应力减小。

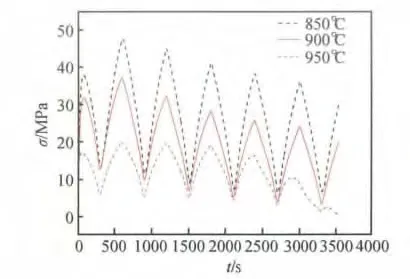
图3 应力-时间关系曲线Fig.3 Relationships between stress and time

2.2 本构方程的建立

以图4 所示900℃温度下的应力-应变曲线为例，由于在刚开始变形时不太稳定以及在后期变形失稳应力下降迅速，容易导致数据失真，因此，本工作在求取超塑性本构方程时，只取每一温度下的第4 或5 周期的应变速率上升阶段的数据进行计算，从而保证所求本构方程的准确性与真实性。

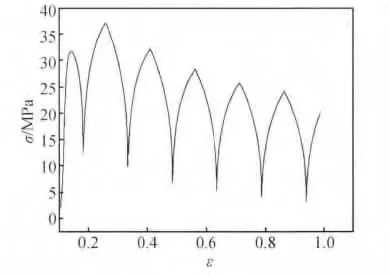
图4 900℃下的应力-应变曲线Fig.4 Relationship between stress and strain at 900℃

本工作采用Arrhenius 模型建立本构方程，并应用origin 数据处理软件进行数据回归与拟合分析。Arrhenius 模型表示材料的本构关系有以下三种形式:

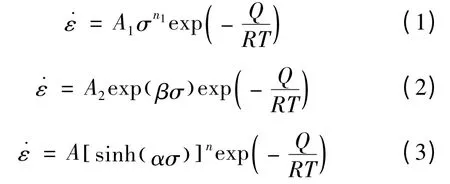
由于本实验都是在相变点以下进行的，且变形温度相差仅为50℃，影响不大，故认为激活能Q 在该变形温度附近的小范围内是固定不变的。即可对式(1)、(2)和(3)两边取对数，得:

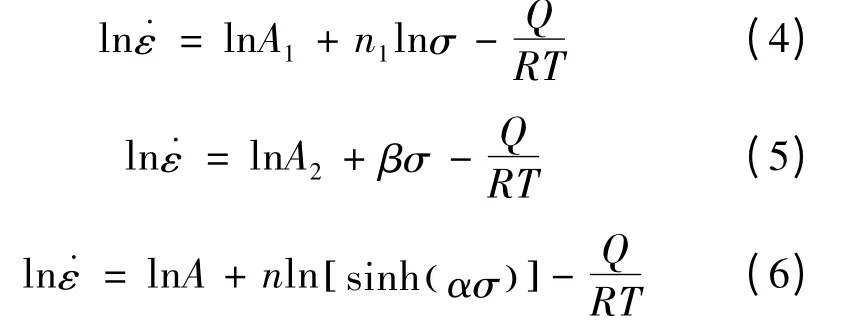
通过对实验数据的计算与处理，可绘出ln ˙εlnσ，ln ˙ε-σ 的关系曲线(图5，图6)并进行线性回归。

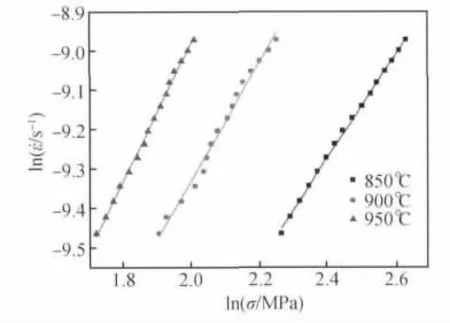
图5 应变速率与对数应力之间的关系Fig.5 Relationship between strain rate and logarithmic stress

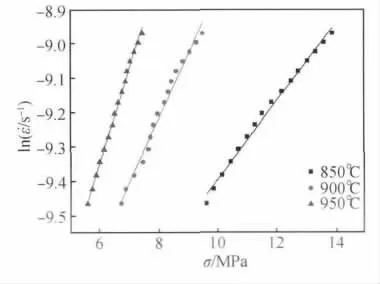
图6 应变速率与应力之间的关系Fig.6 Relationship between strain rate and stress

式(4)称为幂函数型方程，对流动应力较低的材料适用;式(5)称为指数型方程，对流动应力较高的材料适用;式(6)称为双曲正弦型方程，对这两类材料均有较好的适用性。根据参考文献［17］、［18］可知，双曲正弦型Arrhenius 方程中的α 值可由β 与n1的比值获得。从式(4)和(5)看出，ln ˙ε－lnσ 和ln ˙ε－σ 的斜率分别近似表示n1和β，拟合出来的结果如图5 和图6 所示，三组数据取平均值后，n1=1.53507 ，β = 0.19127 ，对应的由式(6)变形得:

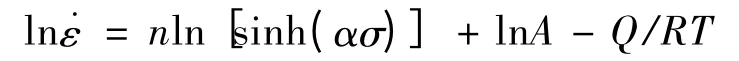
其中，

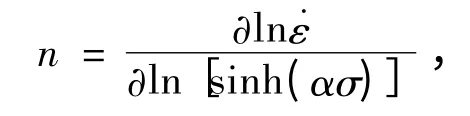
由式(6)另外变形得:

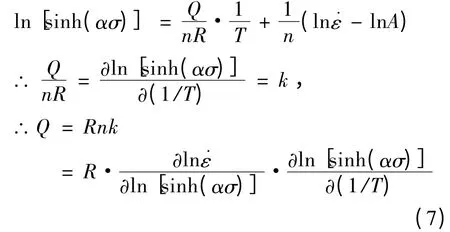
式中，R 是气体常数，为8.314J·mol－1·K－1，图7和图8 中的斜率即式(7)中的n 和k 的值，拟合得n= 1.14257，k = 22.8167 ，代入式(7)可以得出Q =8.314 ×1.14257 × 22.8167 = 216.743 kJ/mol。热激活能反映合金热变形过程中回复和再结晶进行的难易程度。本研究中求得的热激活能Q =216.743 kJ/mol，大于纯α 钛的自扩散激活能204kJ/mol，也大于纯β钛的自扩散激活能161kJ/mol。初步认为TA15 钛合金的热变形与动态再结晶有关。TA15试样的金相组织如图9 所示，从图中看出该组织为等轴组织，α 相含量偏少，并隐约含有少量的次生α相，可以看到原始的β 晶粒已经完全消失，晶界附近和晶内α 相之间的差别消失，白亮的α 条分布较均匀。黑色部分均为β 相，说明发生了α→β 转变，同时部分转变了的β 相发生了再结晶。与图1 的原始组织相比，图9 中的晶粒尺寸整体上更为细小，同时还可以观察到，个别晶粒发生合并长大，在其周围发现了刚刚形核的更为细小的晶粒。

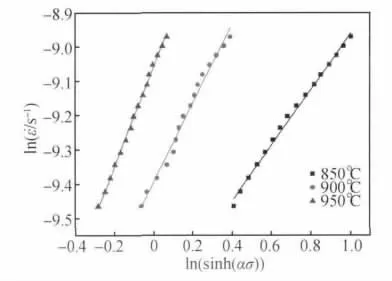
图7 ln［sinh(ασ)］与ln 之间的关系Fig.7 Relationship between ln and ln［sinh(ασ)］

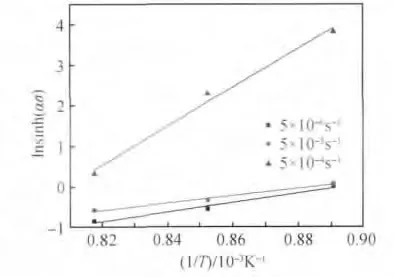
图8 ln［sinh(ασ)］与1/T 之间的关系Fig.8 Relationship between 1/T and ln［sinh(ασ)］

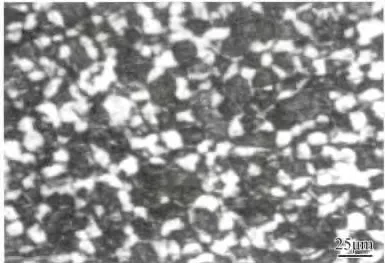
图9 TA15 试样金相组织Fig.9 Microstructure of TA15

由式(6)及图7 可知，ln［sinh(ασ)］－ln拟合后的直线截距，即为ln(A)－Q/RT 的值，将Q，R，T 相应的值代入即可求得不同条件下的lnA 的值，即:

取平均值A =5.62 ×1013，直线的斜率为n 的值，取平均值算得n=1.14257。

将求得的Q，n，A，α 等材料参数代入式(3)中，得到TA15 钛合金在850 ～950℃范围内超塑性变形时的本构方程:

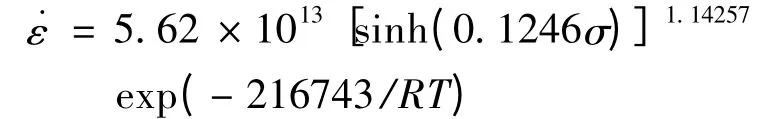
2.3 本构方程的修正

由于Arrhenius 型双曲正弦方程可以表示为σ= f(˙ε，T)，则将本构方程表示如下式:

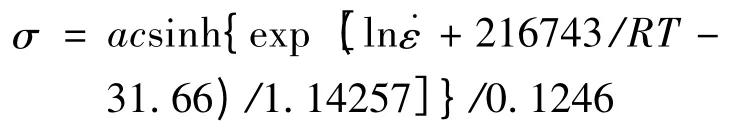
通过计算，在用于构建本构方程的实验数据点中，误差小于15% 的实验数据点占总数据点的70%，误差小于10%的实验数据点占总数据点的49%。图10 为所构建本构方程的误差精度效果图，图中两条直线组成的楔形带为满足相对误差小于和等于15%的误差带，中间一条直线上的点是实验值与计算值相等的点。从图10 可以看出，相当一部分点落在15%的误差带外。

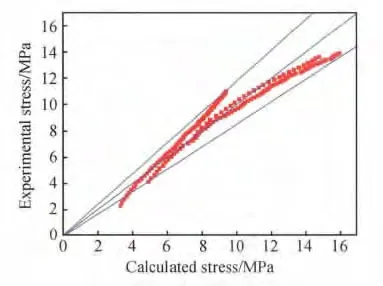
图10 计算应力与实验应力分散图Fig.10 The calculated stress with the experimental stress scatter diagram

以上分析表明，所构建本构方程的精度不足，需对现有的本构方程加以修正。

通过非线性曲线拟合，综合优化分析计算软件1stopt 来对现有的本构方程进行修正。修正设置如下:以本构方程右边的量即Q，n，A，α 和ln的调节值以及常数等六个量为参数，以ln和T 为自变量，把实验所得σ实作为因变量，优化算法为麦夸特法(Levenberg-Marquardt)+通用全局优化法，通过程序中非线性回归，得出六个参数的数值，可使本构关系得到修正，修正后的方程如下所示:

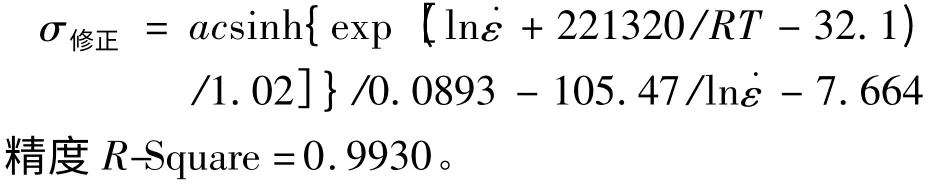
图11 为利用1stopt 软件进行非线性回归拟合后的双线图，其中，蓝颜色的曲线表示σ实曲线，红颜色的曲线表示σ修正曲线，红颜色曲线与蓝颜色曲线的偏差即表示σ修正与σ实的偏差。

通过计算，在用于构建本构方程的实验数据点中，误差小于15% 的实验数据点占总数据点的96.6%，误差小于10%的实验数据点占总数据点的94.2%。图12 为修正本构方程后的误差精度效果图，图中两条直线组成的楔形带为满足相对误差小于和等于15%的误差带，中间一条直线上的点是实验值与计算值相等的点。从图12 可以看出，所有的点几乎都落在15%的误差带内。以上检验表明，修正的本构方程的精度很高。

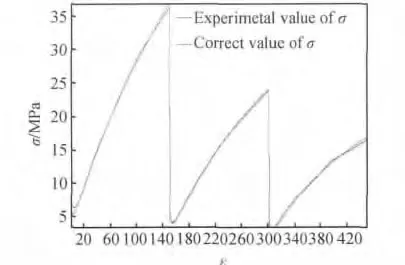
图11 实验数据的拟合双线图Fig.11 Double figure of fitting the experimental data

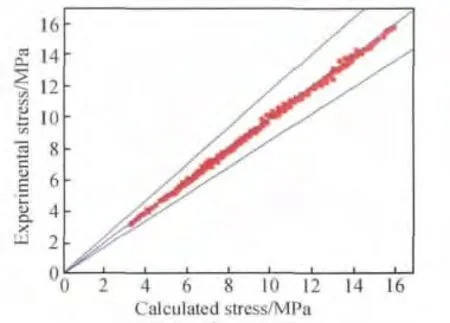
图12 修正后计算应力与实验应力散点图Fig.12 The calculated stress with the experimental stress scatter diagram after correction

图13 为不同温度下按本研究所构建的本构方程求出的流动应力与实验值的比较图。从图13 可以看出根据本研究所构建的本构方程计算所得的流动应力值与实验数据吻合程度较好。以上的误差分析表明，构建的TA15 合金的本构方程有很好的精度，可作为有限元模拟的本构方程。

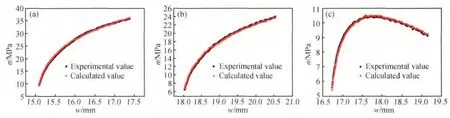
图13 不同温度下流动应力计算值与实验值比较Fig.13 The flow stress calculation value and experimental value comparison in different temperatures(a)850℃;(b)900℃;(c)950℃

3 结 论

(1)TA15 钛合金的流动应力对变形温度较为敏感，随着温度的升高，峰值应力呈逐渐减小的趋势，软化机制作用愈发明显。

(2)TA15 钛合金在900℃附近的超塑性较好，应用应变速率循环法进行拉伸试验，伸长率达到了846%。

(3)在对拉伸实验数据分析的基础上，计算出TA15 钛合金动态再结晶激活能Q ＞纯α 钛的自扩散激活能，结合金相组织分析得出TA15 钛合金热变形发生了动态再结晶;采用Arrhenius 模型建立本构方程，应用origin 数据处理软件进行数据分析，求得TA15 在850 ～950℃范围内超塑性变形的本构方程。

(4)在利用经典模型Arrhenius 方程建出本构关系后，把ln及温度T 作为自变量，把实验所得σ实作为因变量，通过1stopt 软件非线性回归拟合便可使本构关系得到修正，修正后本构的精度可达99.3%，最终得到的流动应力值与实验数据吻合程度也较好。

［1］朱知寿. 我国航空用钛合金技术研究现状及发展［J］.航空材料学报，2014，34(4):44 －50.(ZHU Z S. Recent research and development of titanium alloys for aviation application in China［J］. Journal of Aeronautical Materials，2014，34(4):44 －50.)

［2］申发兰，TA15 钛合金高温变形规律研究［D］. 南京:南京航空航天大学，2013.(SHEN F L，Study on Hot Deformation Rule of TA15 Titanium Alloy［D］.Nan Jing:University of Nan Jing Aeronautics and Astronautics，2013.)

［3］陈洋，裴传虎，李臻熙，等. α +β 钛合金在高应变率下得动态力学性能［J］. 航空材料学报，2013，33(6):8 －12.(CHEN Y，PEI C H，LI Z X，et al. The dynamic mechanical properties of α + β titanium alloys at high strain rates［J］. Journal of Aeronautical Materials，2013，33(6):8 －12.)

［4］曾立英，赵永庆，李丹柯，等.热处理对一种两相钛合金超塑性及组织的影响［J］. 西安工业学院学报，2005，25(4):374 －380.(ZENG L Y，ZHAO Y Q，LI D K，et al. Effect of heat treatment on two-phase titanium alloy superplasticity and organizations［J］. Xi'an Polytechnic University，2005，25(4):374 －380.)

［5］FAN X G，YANG H，GAO P F，et al. Prediction of constitutive behavior and microstructure evolution in hot deformation of TA15 titanium alloy［J］. Materials ＆ Design，2013，51:34 －42.

［6］郭萍，赵永庆，洪权，等.加工工艺对TA15 合金组织和性能的影响［J］.材料热处理学报，2013，34(1):49 －52.(GUO P，ZHAO Y Q，HONG Q，et al. Effects of processing on the microstructure and properties of TA15 alloy［J］.Materials and Heat Treatment，2013，34(1):49 －52.)

［7］于兰兰，毛小南，李辉.温度对TA15 损伤容限型钛合金疲劳裂纹扩展行为的影响［J］.稀有金属快报，2007，26(12):20 －23.(YU L L，MAO X N，LI H. Effects of temperature on fatigue crack growth behavior of TA15 damage tolerance limit type titanium alloys［J］. Rare Letters，2007，26(12):20 －23.)

［8］WANG G C，FU M W，DONG H B，et al. Superplasticity deformation of Ti-6Al-2Zr-1Mo-1V induced by the cyclic change of strain-rate and MaxmSPD［J］. Journal of Alloys and Compounds，2010，491:213 －217.

［9］WANG G C，FU M W，CAO C X，et al. Study on the maximum m superplasticity deformation of Ti-6. 5Al-3.5 Mo-1.5Zr-0. 3Si alloy［J］. Materials Science and Engineering A，2009，513:32 －41.

［10］BALASUBRAHMANYAM V V，PRASAD Y V R K. Deformation behavior of beta titanium alloy Ti-10V-4.5Fe-1.5Al in hot upset forging［J］. Materials Science and Engineering:A，2002，336:150 －158.

［11］ZHANG Y S，SUN Y. Investigation on Constitutive Equations for TA15 during hot working［J］. Applied Mechanics and Materials，2012，184:1492 －1496.

［12］李成铭，李萍，赵蒙，等. TA15 钛合金高温压缩变形行为与组织研究［J］. 航空材料学报，2013，33(3):25 －29.(LI C M，LI P，ZHAO M，et al. Behavior and organization Studies of TA15 titanium alloy during hot compression deformation［J］. Journal of Aeronautical Materials，2013，33(3):25 －29.)

［13］沈昌武，杨合，孙志超，等. 基于BP 神经网络的TA15钛合金本构关系建立［J］. 塑性工程学报，2007，14(4):101 －104.(CHEN C W，YANG H，SUN Z C，et al. Established constitutive relationship of TA15 titanium based on BP neural network［J］. Journal of Plasticity Engineering，2007，14(4):101 －104.)

［14］QUAN G Z，TONG Y，ZHANG Y W，et al. Constitutive Relationship of TA15 Alloy and its Application in the Hammer Forging Process Simulation［J］. Advanced Materials Research，2010，102:516 －520.

［15］梁业，郭鸿镇，刘鸣，等. TA15 合金高温本构方程的研究［J］. 塑性工程学报，2008，15(4):150 －154.(LIANG Y，GUO H Z，LIU M，et al. Research on constitutive equation of TA15 alloy in high temperature ［J］.Plasticity Engineering，2008，15(4):150 －154.)

［16］徐文臣，单德彬，李春峰，等. TA15 钛合金的动态热压缩行为及其机理研究［J］. 航空材料学报，2005，25(4):10 －19.(XU W C，SHAN D B，LI C F，et al. Dynamic thermal compression behavior and mechanism of TA15 titanium［J］. Journal of Aeronautical Materials，2005，25(4):10－19.)

［17］CAI J，LI F G，LIU T Y，et al. Constitutive equations for elevated temperature flow stress of Ti-6Al-4V alloy considering the effect of strain［J］. Materials and Design，2011，32:1144 －1151.

［18］张小刚，潘清林，梁文杰，等.01570 铝合金热压缩变形的流变应力本构方程［J］. 锻压技术，2009，34(1):139－142.(ZHANG X G，PAN Q L，LIANG W J，et al. Constitutive equation of flow stress for 01570 aluminum alloy during hot compression deformation［J］. Forging Technology，2009，34(1):139 －142.)