基于疲劳裂纹萌生机理的铝合金疲劳寿命可靠性评估方法
2014-11-16谭晓明张丹峰陈跃良
谭晓明, 张丹峰, 陈跃良, 金 平
(海军航空工程学院,山东 青岛266041)
铝合金由于具有密度低、比强度和断裂韧度高、塑性和加工性能好等一系列优点,一直是飞机结构的主体材料。疲劳断裂是飞机铝合金结构的主要失效形式,对使用寿命和可靠性构成严重威胁。
近年来,国内外学者针对航空铝合金的疲劳裂纹萌生与扩展机理开展了大量研究,这些研究主要是基于材料微观结构的疲劳性能表征的研究,目前已成为航空界研究的热点方向之一[1,2],研究结果表明,在循环载荷作用下材料疲劳裂纹一般在其初始不连续状态[1,3~8]或者微观非均质[9~12]处萌生,如第二相、夹杂、微孔和晶界等。研究结果表明,对于内部有微孔的铸造铝合金,疲劳裂纹一般萌生于微孔[1];对于无微孔的铝合金轧制板材,疲劳裂纹一般萌生于尺寸较大的第二相[6,8,11,14];对于材料内部无尺寸较大的微观非均质,疲劳裂纹一般萌生于晶粒[1],具体材料的疲劳裂纹萌生机理取决于材料厚度、热处理状态、表面处理工艺和加载的应力水平等。可见,材料微观结构与疲劳机制、疲劳行为有着直接的关系,材料分散性直接导致疲劳寿命的分散性。
但是,到目前为止,这些研究工作都尚未建立材料微观结构-疲劳裂纹萌生机理-疲劳寿命分散性三者之间的对应关系模型。因此,为提高疲劳寿命预测精度,有必要基于裂纹萌生微观机理进行寿命评估研究。本工作以新型铝合金2B06 为研究对象,通过研究材料微观结构对疲劳裂纹萌生的作用机制,运用概率断裂力学,获得微观结构尺寸分布规律与概率疲劳寿命的对应关系。
1 疲劳试验
试验材料为2B06 铝合金薄板材料,其化学成分如表1 所示。

表1 2B06 铝合金化学成分(质量分数/%)Table 1 Chemical composition of 2B06 aluminum alloy (mass fraction/%)
疲劳试验件外形与尺寸如图1 所示,试验件表面打磨光滑至镜面。
借助Material Testing System 810 液压伺服疲劳试验机,针对如图1 所示的4 组2B06 试验件分别进行应力比0. 06,不同载荷峰值σmax= 282MPa,250MPa,240MPa,220MPa 的等幅疲劳试验,每级应力水平试验件数量为15 件。
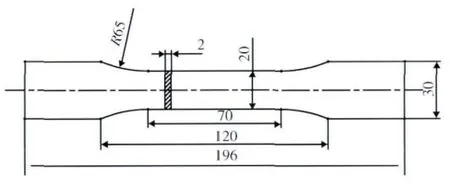
图1 试件外形与尺寸(单位:mm)Fig.1 Specimen dimension and configuration (unit:mm)
2 材料微观结构几何尺寸分布规律
经分析知该新型铝合金主要有两种第二相,即θ 相和S 相,如图2 所示。JSM-6700F 场发射扫描电镜对ST 平面第二相进行能谱分析,如图3 所示。根据2000 系列航空铝合金的微观组织特征,通过能谱分析可知,2B06 铝合金θ 相在金相图(图2)中为黑色圆形,在扫描电镜下(图3)为亮白色,化学组成为CuAl2;S 相在金相图(图2)中为灰色片状,在扫描电镜下(图3)为暗灰色,化学组成为Al2CuMg。

图2 2B06 铝合金金相组织结构Fig.2 Microstructure of 2B06 aluminum alloy
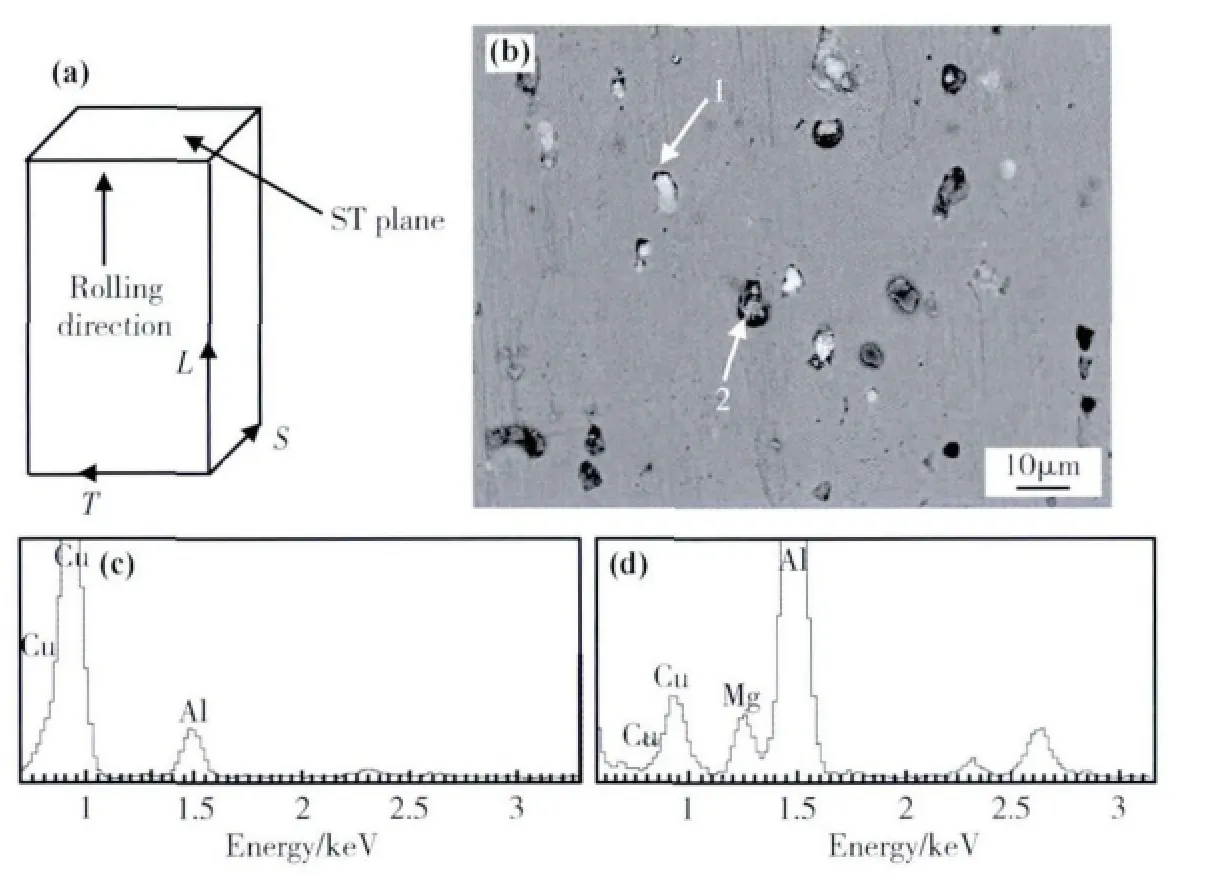
图3 2B06 铝合金材料微观结构能谱分析 (a)ST 平面示意图;(b)2B06 铝合金微观结构图;(c)图b 中的1 点;(d)图b 中的2 点Fig.3 Energy dispersive spectroscopy analysis of 2B06 aluminum alloy (a)ST plan;(b)2B06 aluminum alloy micro structure;(c)region 1 in (b);(d)region 2 in (b)
通过KH-7700 测量软件分别测得θ 相的直径(样本数量为216个)、S 相的长度和宽度(样本数量为152个),分别采用正态、对数正态、Weibull、Logistic 和Gumbel 分布对测量数据进行检验,结果表明这些尺寸参数的最佳分布形式为对数正态分布。
经数据拟合分析得到θ 相直径(d)、S 相宽度(a)和长度(2c)的概率密度函数分别见式(1)、式(2)和式(3),概率分布拟合曲线分别见图4、图5 和图6。
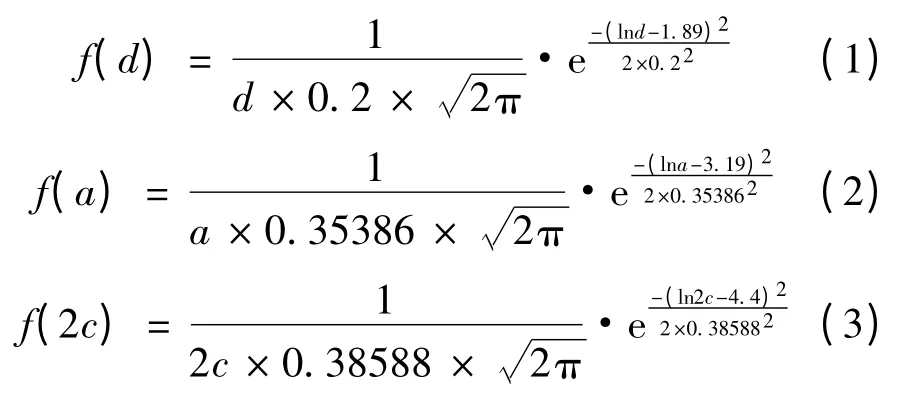
3 疲劳裂纹萌生机理
借助扫描电镜对该型铝合金光滑试件的疲劳断口分析可知,除少部分疲劳裂纹萌生于表面加工缺陷外,疲劳裂纹大部分萌生于尺寸较大的S 相,如图7 为萌生疲劳裂纹的S 相尺寸测量的示意图,通过对萌生疲劳裂纹的S 相宽度的统计分析,得到其分布规律,见式(4)。


图4 θ 相直径d 概率密度函数拟合曲线Fig.4 Probability distribution function of θ phase diameter

图6 S 相晶粒长度(2c)概率分布拟合曲线Fig.6 Probability distribution function of S phase length

图7 疲劳断口形貌Fig.7 Macro morphology fatigue fracture
4 基于裂纹萌生微观机理的疲劳寿命理论模型及验证
4.1 理论模型
根据扫描电镜断口分析获得的2B06 铝合金疲劳裂纹萌生机理,可将第二相当量化为半椭圆表面裂纹,宽度为2c,深度为a,如图8 所示。

图8 第二相与裂纹的理论模型示意图Fig.8 Theoretical model for second phase and fatigue crack
文献[14,15 ~17]假设疲劳裂纹萌生于某个S相是随机的,基于铝合金裂纹萌生微观机制建立疲劳寿命理论模型,全寿命NT的表达式如下
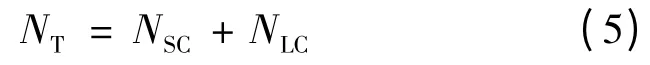
式(5)中NSC为短裂纹扩展寿命,即萌生于材料微观结构(S 相)的短裂纹到长裂纹之前的扩展寿命;NLC为长裂纹扩展寿命。裂纹扩展速率采用Walker 公式,经积分后分别得到NSC和NLC的数学表达式[18~22],式(5)可变换为

式(6)中a0即为材料S 相尺寸,根据式(1)和式(2)取值;CSC和CLC分别为短裂纹和长裂纹扩展系数,服从对数正态分布[18~22];ath为短裂纹与长裂纹之间的临界长度,参考文献[23]确定ath的取值范围为0.5 ~1mm 之间,服从对数正态分布。
4.2 试验验证
根据式(2)和式(3)表示的第二相尺寸分布规律,运用Monte Carlo 方法对疲劳寿命进行理论分析,结果见表2 和图9。经分析知,萌生疲劳裂纹的第二相的平均宽度(2c)为81.4μm,深度(a)为24.3μm。从表2 和图9 可以看出,理论计算寿命均值与试验寿命均值比较吻合,最大误差为8.5%;同级应力水平,理论计算寿命最小值均比试验寿命最小值小,理论计算寿命最大值均比试验寿命最大值大,分析其原因是由于仿真抽样的理论计算寿命数据量比试验寿命数据量大得多,理论计算寿命更能反映母体的分布特征。从表2 可知,理论计算寿命最小值与试验寿命最小值误差大于中值对应的误差,而理论计算寿命最大值与试验寿命最大值两者误差较大,最大到达了88%,分析其原因是由于理论计算寿命的样本远大于试验寿命的样本。

表2 理论计算结果与疲劳试验结果对比情况Table 2 Contrast between calculated life and fatigue testing life
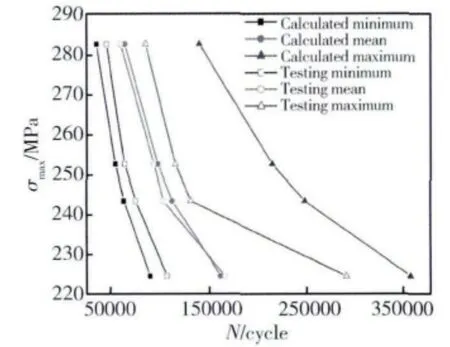
图9 理论计算寿命与试验寿命对比分析Fig.9 Comparison between calculated life and fatigue testing life
根据文献[24]知,对于任意可靠度p 对应的试验寿命计算公式为

当置信度γ = 95%,可靠度p 分别取90%,95%,99%和99.9%,根据本章所建立的理论计算模型计算疲劳寿命,结果列入表3 ~表6,根据式(5)分别计算试验寿命,结果也列入表3 ~表6 中。
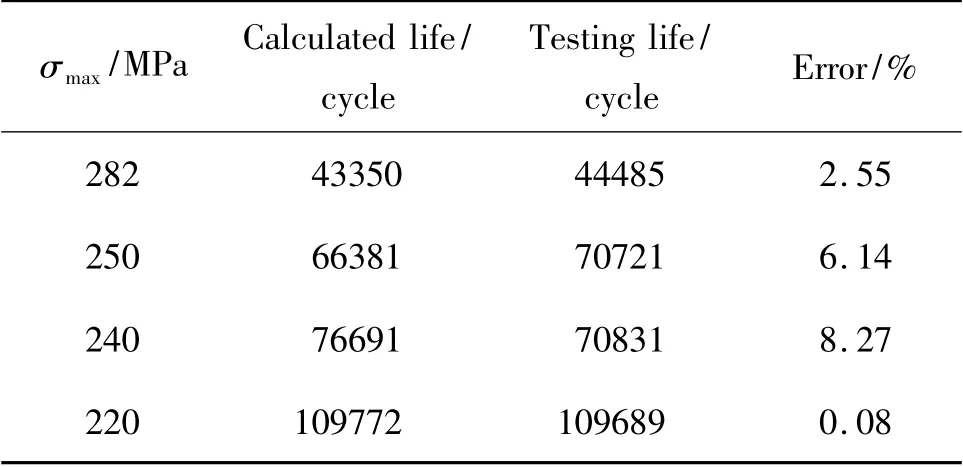
表3 可靠度为90%时理论计算寿命与试验寿命的对比情况Table 3 Comparison between calculated life and testing life for reliability being 90%

表4 可靠度为95%时理论计算寿命与试验寿命的对比情况Table 4 Comparison between calculated life and testing life for reliability being 95%
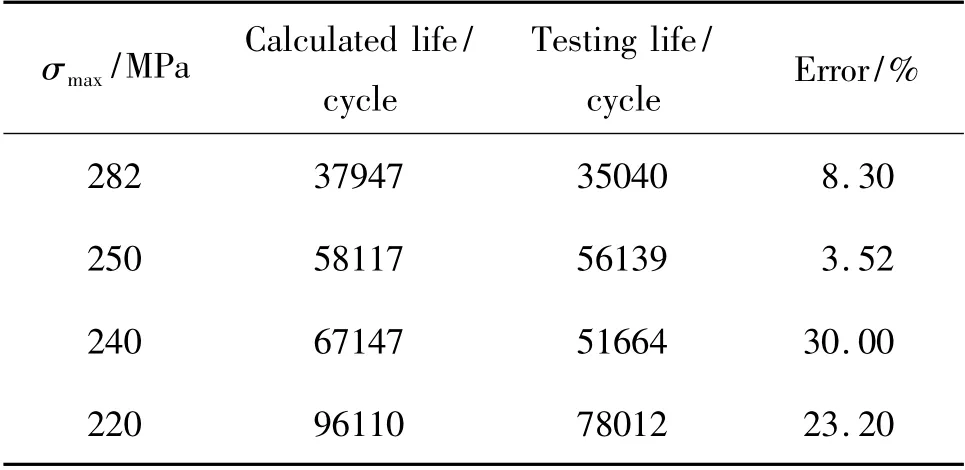
表5 可靠度为99%时理论计算寿命与试验寿命的对比情况Table 5 Comparison between calculated life and testing life for reliability being 99%

表6 可靠度为99.9%时理论计算寿命与试验寿命的对比情况Table 6 Comparison between calculated life and testing life for reliability being 99.9%
从表3 ~表6 得知,当可靠度较低时(可靠度为50%,90%和95%),理论计算寿命与试验寿命误差较小,比较接近;当可靠度较高时(可靠度为99%和99.9%),两者差别较大,理论计算寿命均大于试验寿命,如当可靠度为99.9%,应力水平为240MPa、应力比为0.2 时,理论计算寿命为试验寿命1.5 倍,随着可靠度增大,理论计算寿命与试验寿命的误差增大,如表6 所示最大误差达到56.01%,分析其原因可能是受到试验样本限制的原因。
5 结论
(1)对于2B06 铝合金光滑轧制薄板材料,疲劳裂纹一般在尺寸较大的S 相(Al2CuMg)处萌生,θ相和S 相尺寸均服从对数正态分布。
(2)通过验证知,可将萌生疲劳裂纹的S 相当量化为半椭圆表面裂纹,其平均宽度为81.4μm,平均深度为24.3μm,分析得到S 相深度的累积分布函数
(3)提出的基于疲劳微观机制的疲劳寿命可靠性评估方法能较好地模拟试验件疲劳寿命随机性,经试验验证该评估方法是合理可行的。
[1]蔡彪,郑子樵,廖忠全,等. 航空铝合金耐疲劳损伤特征微结构研究现状[J].材料导报,2010,24(9):134 -138.(CAI B,ZHENG Z Q,LIAO Z Q,et al. The microstructure properties affecting the fatigue performance in aluminum alloy for aviation industry[J]. Materials Review,2010,24(9):134 -138.)
[2]TAN X M,ZHANG D F. Research on initial discontinuity state of an advanced aluminum alloy rolling thin plate[C]// International Conference on Manufacturing Science and Engineering,Zhuhai,Guangdong,China,26 -28 December,2009.
[3]LIAO M,MERATI A. Statistical analysis of the initial discontinuity state (IDS)data of 2024-T3 aluminum alloy[C]//Canadian Aeronautics and Space Institute 50th AGM and Conference 16th Aerospace Structures and Materials Symposium Montréal,28 -30 April,2003.
[4]MERTATI A,EASTAUGH G. Determination of fatigue related discontinuity state of 7000 series of aerospace aluminum alloys[J]. Engineering Failure Analysis,2007,14:673 -685.
[5]LAZ P J,CRAIG B A,HILLBERRY B M. A probabilistic total fatigue life model incorporating material inhomogeneities,stress level and fracture mechanics[J]. International Journal of Fatigue,2001,23:S119 -S127.
[6]PAYNE J,WELSH G,CHRIST R J. Observations of fatigue crack initiation in 7075-T651[J]. International Journal of Fatigue,2010,32:247 -255.
[7]LU Y,GHARGHOURI M,TAHER F,et al. Numerical study of the casting features on the fracture and debonding of Mg17Al12in AM60B Mg alloy under high cycle fatigue condition[J]. Materials and Design,2009,30:1994 -2005.
[8]HARLOW D G,WANG M Z,WEI R P. Statistical analysis of constituent particles in 7075-T6 aluminum alloy[J].Metallurgical and Materials Transactions:A,2006,37:3367 -3373.
[9]GERHART S. Reliability-statistical methods in fracture and fatigue[J]. Engineering Fracture Mechanics,2007,74:2917 -2918.
[10]MERATI A. A study of nucleation and fatigue behavior of an aerospace aluminum alloy 2024-T3[J]. International Journal of Fatigue,2005,27:33 -44.
[11]MERTI A,EASTAUGH G. Determination of fatigue related discontinuity state of 7000 series of aerospace aluminum alloys[J]. Engineering Failure Analysis,2007,14:673 -685.
[12]LIAO M. Probabilistic modeling of fatigue related microstructural parameters in aluminum alloys[J]. Engineering Fracture Mechanics,2009,76:668 -680.
[13]CAPPELLI M D,CARLSON R L,KARDOMATEAS G A.The transition between small and long fatigue crack behavior and its relation to microstructure[J]. International Journal of Fatigue,2008,30:1473 -1478.
[14]丁传富,刘建中,吴学仁. TC4 钛合金和7475 铝合金的长裂纹和小裂纹扩展特性的研究[J]. 航空材料学报,2005,25(6):11 -17.(DING C F,LIU J Z,WU X R. An investigation of small crack and long crack propagation behavior in titanium alloy TC4 and aluminum alloy 7475-T7351[J].Journal of Aeronautical Materials,2005,25(6):11 -17.)
[15]HARLOW D G,NARDIELLO J,PAYNE J. The effect of constituent particles in aluminum alloys on fatigue damage evolution:statistical observations[J].International Journal of Fatigue,2010,32:505 -511.
[16]CAPPELLI M D,CARLSON R L,KARDOMATEAS G A.The transition between small and long fatigue crack behavior and its relation to microstructure[J].International Journal of Fatigue,2008,30:1473 -1478.
[17]WEILAND H,NARDIELLO J,ZAEFFERER S,et al.Microstructural aspects of crack nucleation during cyclic loading of AA7075-T651[J]. Engineering Fracture Mechanics,2009,76:709 -714.
[18]TAN X M,CHEN Y L,JIN P. Corrosion fatigue life prediction of aircraft structure based on fuzzy reliability approach[J].Chinese Journal of Aeronautics,2005,18(4):346 -351.
[19]TAN X M,CHEN Y L,JIN P. Prediction approach for corrosion fatigue life of aircraft structure based on probabilistic fracture mechanics[J]. Key Engineering Material,2006,324/325:943 -946.
[20]JIN P,TAN X M,CHEN Y L. Reliability approach and experimental validation for fatigue life prediction of aircraft structure under corrosion environment[C]// LI S C,WANG Y J,HUANG P. Progress in Safety Science and Technology,Beijing:Science Press,2006:2402 -2406.
[21]PAN S,SANKARAN M. Damage tolerance approach for probabilistic pitting corrosion fatigue life prediction[J].Engineering Fracture Mechanics,2001,68:1493 -1507.
[22]HARLOW D G,WEI R P. A Probability model for the growth of corrosion pits in aluminum alloys induced by constituent particles[J]. Engineering Fracture Mechanics,1998,59(3):305 -325.
[23]DOLLEY E J,WEI R P. Importance of chemically shortcrack-growth on fatigue life[C]// 2nd Joint NASA/FAA/DoD Conference on Aging Aircraft,Williamsburg,VA,1998:679 -687.
[24]HB/Z112 -86,材料疲劳试验统计分析方法[S].
