55%Al-Zn合金熔体结构的从头算研究

邢文国， 孟宪兴， 冯维春， 张长桥

(1. 山东省生物化学工程重点实验室，济南250014;2. 山东大学 化学与化工学院，济南250061)

钢铁表面热镀耐蚀金属镀层，是其防止大气腐蚀的主要方法之一［1］。钢铁表面热镀耐蚀金属物理机制的研究成为实验和理论工作者共同关注的问题。较早发展和应用起来的是热镀纯锌镀层，但其耐蚀性能有限。热镀铝镀层的耐蚀效果明显优于热镀锌，但由于铝的熔点较高，化学活性大，铝液与钢铁表面浸润性差，而使得镀层质量和结构控制不够稳定。最近几年发展起来的热镀铝锌合金，综合了纯锌、纯铝镀层各自的特点，具有良好的耐腐蚀性和较好的阴极保护性能，镀层质量易于控制，镀层结构稳定。目前，研究和发展较快的有5%Al－Zn 的Galfan 和55%Al－Zn 的Galva1um 合金镀层［2～9］。尤其是后者，在工业大气中其耐蚀性比纯锌镀层优良得多，与纯铝镀层相近。

实验发现5%Al－Zn 和55%Al－Zn 合金镀层可以产生较好的耐蚀性，但是铝含量对Al－Zn 合金耐蚀性能的影响不遵从线性规律。目前对这一问题的物理机制并不清楚，其难点在于该合金的高温熔体结构以及冷却过程直接影响最终耐蚀效果，因此深入了解该合金熔体的结构及电子结构，以此为基础进一步研究冷凝过程中其结构的变化规律，对于材料的成分设计和寻找最佳工艺条件以获得更好的耐蚀性能有着非常重要的实际意义。实验上可以使用X 射线衍射或中子散射等技术得到合金熔体的结构参数，但很难给出熔体局域结构细节的描述。另外，由于合金熔体温度较高，实验难度比较大。

第一性原理分子动力学模拟方法可以给出熔体结构的描述。相对于经典的分子动力学，该方法的优点在于不需要任何调整参数，并对电子结构进行优化，原子间的相互作用对化学环境的依赖性不强，可以给出原子成键的变化对熔体局域结构的影响，现已成为了解熔体微观结构信息的主要手段之一，并取得了一系列进展［10～12］。

本工作采用第一性原理分子动力学模拟方法对高温55%Al－Zn 合金熔体进行了研究。给出了熔体的结构和动力学性质，为进一步研究其冷却过程变化规律，从而更有效地确定加工工艺，提供理论基础。

1 计算方法

计算使用VASP 程序包(vienna ab initio simulation program)［13］，采用了Wang 和Perdew［14］发展的广义的共轭梯度近似方法(generalized conjugate gradient approximation，GGA)描述电子交换－相关能，使用Vanderbilt 型超软赝势描述电子与离子间的相互作用［15］。在分子动力学模拟过程中，对每一构型都进行了电子结构的优化。模拟过程使用了正则系综并采用Nosé 热浴法来控制系统的温度［16］。

较之传统分子动力学模型，从头算分子动力学模型计算量更大，目前计算体系多数在100 粒子左右。但是，由于从头算动力学方法考虑了体系的电子结构，所得结果更可靠［17，18］。在55%Al－Zn 合金熔体结构的计算中，使用含有80个原子的立方晶胞模拟熔体结构(包含60个Al 原子和20个Zn 原子)，温度取为恒定的923K。并采用实验密度，取变量点描述布里渊区。电子波函数向平面波展开，截断能为250eV。用Verlet 算法求解离子的运动方程并取时间步长为3fs。平衡后，感兴趣的物理量取自9ps 的统计平均值。同时，为验证结果的正确性，也采用同样的方法计算了Al 和Zn 熔体的结构参数，并与实验结果进行了比较。

2 结构分析方法

在液态结构的分子动力学模拟研究中，各种物理量取系综统计平均值。

2.1 结构因子

在计算中，取液态合金的偏结构因子为:

粒子的位置r 由从头算分子动力学模拟得到;Nα是第α 种成分原子的数目;括号［…］代表对系综和时间求平均。

2.2 双体相关函数

在多元液体中以α 粒子为中心在r 处发现β 粒子的数密度为:

式中，Nα为第α 种成分的原子数。gαβ(r)即为偏双体相关函数(partial pair correlation function)。

2.3 均方位移和速度自相关函数

分子动力学计算中原子不停地移动。以rαi(t)表示t 时刻第i个α 种粒子的位置，则粒子位移平方的平均值称为均方位移(mean square displacement，MSD)为:

均方位移与原子扩散系数符合爱因斯坦扩散定律［19］:

以Vα(t)表示t 时刻第α 种粒子的速度，则粒子的速度自相关函数(velocity autocorrelation function，VACF)定义为［20］:

与之相应的光谱密度由下式给出［21］:

3 结果与讨论

3.1 熔体结构因子计算值与实验结果的比较

55%Al－Zn 合金熔体结构因子在实验上采用X射线衍射测得。图1 为55%Al－Zn 合金熔体结构因子的计算值与实验结果的比较，从图中可以看出这两种方法得到的结果符合较好。由此可见，从头算分子动力学方法对熔体结构的描述是合理的。

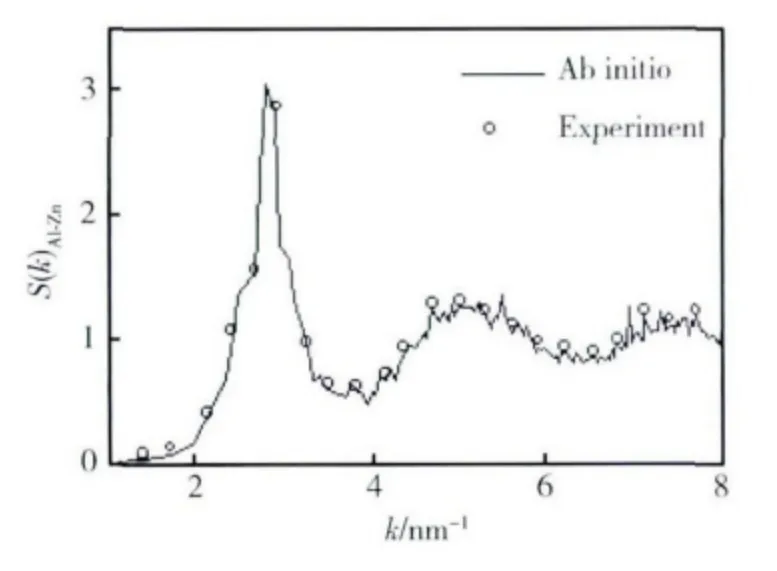
图1 55%Al－Zn 合金熔体结构因子的计算值与实验值Fig.1 The comparison of structure factor of 55% Al－Zn melt between experimental value and calculated value

3.2 55%Al-Zn 合金熔体的结构因子

计算得到的55%Al－Zn 合金熔体的三个偏结构因子分别见图2，由图2 可以看出，偏结构因子SAl－Zn(k)与SAl－Al(k)几乎重合，表明Al 原子的分布在加入Zn 原子后变化不大。由图2 可知，与偏结构因子SAl－Zn(k)相比，SZn－Zn(k)的第二峰变得非常平坦，表明Zn 原子基本上是随机分布的。

3.3 55%Al-Zn 合金熔体的偏双体分布函数

图3 给出计算得到的55%Al－Zn 合金熔体的三个偏双体分布函数，三个偏双体分布函数第一峰的位置差别不大，在55%Al－Zn 合金熔体gZn－Zn(r)的第二峰消失，表明Zn－Zn 间的相关性发生明显改变，而Al－Al 间的相关性变化不大，与55%Al－Zn 合金熔体的双体分布函数几乎重合。

由偏双体分布函数可计算原子配位数:

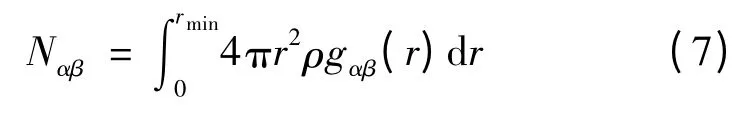
图2 55%Al－Zn 合金熔体中结构因子Fig.2 The calculated structure factor of 55% Al－Zn alloy melt

计算中取截断距离rmin为0.36nm，Al 熔体的配位数为10.10，Zn 熔体的配位数为10.61。Al－Zn 熔体中Al－Al，Al－Zn 和Zn－Zn 的配位数见表1。

表1 Al－Zn 熔体中原子配位数Table 1 The atom coordination number of Al－Zn alloy melt

由表1 可以看出，Al－Zn 熔体中Al－Al 配位数与Al－Zn 配位数的比大约为3∶1，与熔体中原子含量的比值基本一致。这表明Zn 原子在Al－Zn 熔体中第一配位层内是按无规密堆分布的。再考虑到gZn－Zn(r)除存在第一峰外，其他峰几乎观察不到，可以认为Zn 原子在熔体中是均匀分布的。

3.4 原子扩散系数

原子在熔体中的扩散运动可通过研究原子的运动而得到。熔体中原子运动的均方位移见图4。由式(5)得到的原子扩散系数见表2。Al 熔体的原子扩散系数缺乏实验数据，本次研究的计算值与Protopapas 等人的理论预测值符合得较好［22］。Zn 熔体扩散系数的计算值与实验值基本一致［23］。

图4 Al－Zn 熔体中原子的均方位移Fig.4 The mean square displacement of Al atom and Zn atom in Al－Zn alloy melt

表2 Al，Zn 和55%Al－Zn 熔体中原子的扩散系数Table 2 The atom diffusion coefficient of Al，Zn，and Al－Zn alloy melt

3.5 原子速度自相关函数和光谱密度

原子在熔体中的扩散运动也可由速度自相关函数来表示。Al－Zn 熔体中原子的速度自相关函数见图5。与Zn 原子相比Al 原子的速度自相关函数表现为明显的第一谷，这表明周围原子对Al 原子运动的阻碍作用比较强。这一方面与Al 原子的质量较小有关，另一方面是由于Zn 原子的原子半径较小。

由速度自相关函数的傅里叶变换可得到原子运动的光谱密度函数，结果见图6。由光谱密度函数可观测原子运动的频率，图6 中显示出原子Al 和Zn 在熔体中的“阻碍移动”，“阻碍移动”的意义为在熔体中原子的移动受到周围原子的阻碍，结果类似于在一区间中来回移动。由图6 可知，Al 原子光谱密度函数的峰值位于6THz 左右，远大于Zn 原子的2THz，这也说明Al 原子周围的第一近邻Zn 原子形成的笼体对Al 原子运动的阻碍作用较强，同时也说明Al 和Zn 原子间有较强的相互作用。

图5 55%Al－Zn 熔体中原子速度自相关函数Fig.5 The velocity autocorrelation function of the atom in 55% Al－Zn alloy

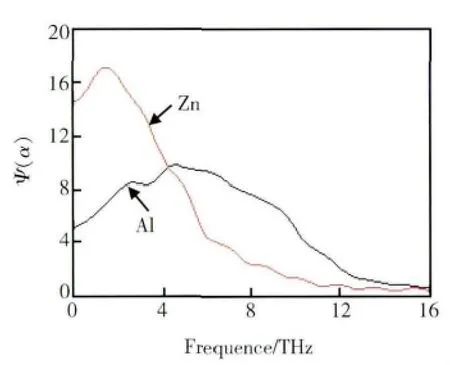
图6 55%Al－Zn 熔体中原子光谱密度函数Fig.6 The spectral concentration function of the atom in 55% Al－Zn alloy

4 结论

(1)采用第一性原理分子动力学模拟方法研究高温55%Al－Zn 合金熔体的结构和动力学性质，熔体结构中Al 原子的分布在加入Zn 原子后无明显变化，而Zn 原子的分布是随机均匀的。

(2)熔体中Al－Al 配位数与Al－Zn 配位数的比大约为3∶1，与熔体中原子含量的比值基本一致。

(3)熔体中Al 原子周围的第一近邻原子形成的笼体对Al 原子运动的阻碍作用较强。

［1］EGGELER G，AUER W，KAESCHE H. On the influence of silicon on the growth of the alloy layer during hot dip aluminizing［J］. Journal of Materials Science，1986，21(9):3348 －3350.

［2］SIMPSON T C. Accelerated corrosion test for aluminumzinc alloy coatings［J］. Corrosion，1993，49(7):550 －560.

［3］BARNARD N C，BROWN S G R. Modelling the relationship between microstructure of galfan－type coated steel and cut－edge corrosion resistance incorporating diffusion of multiple species［J］. Corrosion Science，2008，50(10):2846－2857.

［4］FELIU S，BARRANCO V. Study of degradation mechanisms of a protective lacquer film formulated with phosphating reagents applied on galvanised steel，galvanneal and galfan in exposure to UV/condensation test［J］. Surface ＆Coatings Technology，2004，182(2/3):251 －260.

［5］FELIU S，BARRANCO V. Effect of the incorporation of chromating reagents in an acrylic lacquer applied on galvanised steel，galvanneal and galfan during the UVCON test［J］. Surface ＆ Coatings Technology，2004，182(2/3):318 －328.

［6］PUOMI P，FAGERHOLM H M，SOPANEN A. Parameters affecting long－term performance of painted galvanised steels［J］. Anti－Corrosion Methods and Materials，2001，48(3):160 －171.

［7］CONI N，GIPIELA M L，D'OLIECEIRA A S C M. Study of the mechanical properties of the hot dip galvanized steel and galvalume［J］. Journal of The Brazilian Society of Mechanical Sciences and Engineering，2009，31(4):319 －326.

［8］YANG D，CHEN J S，HAN Q. Effects of lanthanum addition on corrosion resistance of hot－dipped galvalume coating［J］. Journal of Rare Earths，2009，27(1):114 －118.

［9］LIVATYLI H，DUGGAL N，AHMETOGLU M A. Investigation of crack formation on the galvalume coating of roll formed roof panels［J］. Journal of Materials Processing Technology，2000，98(1):53 －61.

［10］GU T，QIN J，XU C，et al. An structural，bonding，and dynamical properties of liquid Fe－Si alloys:ab initiomolecular－dynamics simulation［J］. Phys Rev:B，2004，70(14):144204 －144210.

［11］GU T，BIAN X，QIN J，et al. Ab initio molecular dynamics simulations of liquid structure change with temperature for a GaSb alloy［J］. Phys Rev:B，2004，70(24):245214 －245220.

［12］GU T，BIAN X，QIN J，et al. Ab initio molecular－dynamics simulations of liquid GaSb and InSb［J］. Phys Rev:B，2005，71(10):104206 －104213.

［13］KRESSE G，FURTHMÜLLER J. Efficiency of ab－initio total energy calculations for metals and semiconductors using a plane－wave basis set［J］. Comput Mater Sci，1996，6(1):15 －50.

［14］WANG Y，PERDEW J P. Correlation hole of the spin－polarized electron gas，with exact small－wave－vector and high－density scaling［J］. Phys Rev:B，1991，44(24):13298 －13307.

［15］VANDERBILT D. Soft self－consistent pseudopotentials in a generalized eigenvalue formalism［J］. Phys Rev:B，1990，41(11):7892 －7895.

［16］NOSÉ S. A unified formulation of the constant temperature molecular dynamics methods［J］. Chem Phys，1984，81(1):511 －519.

［17］CAR R，PARRINLLO M. Structural，dynamical，and electronic properties of amorphous silicon:an ab initio molecular－dynamics study［J］.Phys Rev Lett，1988，60(3):204 －207.

［18］SENDA Y，SHIMOJO F，HOSHINO K. The ionic structure and the electronic states of liquid Li－Pb alloys obtained from ab initiomolecular dynamics simulations［J］. J Phys:Condens Matter，2000，12(28):6101 －6112.

［19］MARK A，DANE M，HOYT J，et al. Embedded－atommethod study of structural，thermodynamic，and atomictransport properties of liquid Ni－Al alloys［J］. Phys Rev:B，1999，59(22):14271 －14281.

［20］JEROME J E，WILLIAM W W. Molecular－dynamics calculations of the velocity－autocorrelation function:methods，hard－disk results［J］. Phys Rev:A，1982，26(3):1648－1675.

［21］谷廷坤. 合金熔体局域结构的实验及从头算研究［D］.山东:山东大学 材料科学与工程学院，2005.

［22］PROTOPAPAS P，PARLEE N A D. Theory of transport in liquid metals :Ⅲ:calculation of shear viscosity coefficients of binary alloys［J］. Chemical Physics，1975，11(1):201 －215.

［23］NACHTRIEB N H，FRAGA E，WAHL C. Self－diffusion of liquid zinc［J］. J Phys Chem，1963，67(11):2353 －2355.