基于可靠度与可观度的量测优化配置研究

卢志刚 赵 号 刘雪迎 程慧琳 田莎莎

（1. 燕山大学电力电子节能与传动控制河北省重点实验室 秦皇岛 066004 2. 国网冀北电力有限公司秦皇岛供电公司 秦皇岛 066004 3. 国网石家庄供电公司 石家庄 050000）

1 引言

系统的可观测性、数值稳定性与精确的估计结果是实时状态估计软件充分发挥作用的重要保证。然而，随着电网发展和电力市场的推进，电力系统运行的复杂程度日益增大，经常会遇到一个或几个节点数据完全缺失的情况[1]，造成状态估计软件不能很好地发挥作用。因此，如何优化量测配置，改善现有量测系统，如何合理规划设计未来电网的量测系统，使系统在节点量测信息不完整的情况下可观且具有良好的数值稳定性与估计精度，具有重要的理论和应用研究价值。

目前，关于量测配置方案所采用的方法有遗传算法[2]、模拟退火法[3]、禁忌搜索算法[4]和粒子群算法[5]等，这些算法保证所有母线均可观测且配置数目最小。文献[6-8]考虑到电力网络在拓扑结构发生变化的情况下某些关键线路失去可观测性的严重情况，提出N-1情况下的优化配置方法。但是这些方法均没有考虑装置故障的情况下，造成节点数据完全丢失影响系统可观测性的问题。另外，通信通道的故障也会造成节点信息的丢失，影响系统的可观测性。然而，实际应用中发现即使系统可观，状态估计仍会出现不收敛、收敛结果不理想等情况。系统的可观测性反映的仅仅是系统输出估计状态量的可能性，未能反映系统状态变量估计精度和速度。文献[9]以提高状态估计精度为目标确立配置方案，该文以排列各个母线及其相邻母线状态估计误差的协方差矩阵元素之和作为增加量测配置的依据。

论文引入节点电气介数[10,11]定义和可靠性损失指标；提出可观度的概念并介绍了相应的指标；研究了量测系统优化配置和规划方案；通过算例仿真及结果分析总结本文工作及存在问题。

2 可靠度

2.1 电气介数

“电气介数”被用于关键线路与节点的识别，原因是：“电气介数”能反映出具有较高介数的节点或支路，在网络中承担着较多的信息或物质交换工作，并为大多数信息或物质流量所通过，故其故障对网络的功能必然产生重大影响，因此电气介数很关键。该方法基于电路方程，克服了加权介数模型假设母线间潮流只沿最短路径流动的不足，能有效反映各“发电-负荷”节点对线路与节点的真实利用情况，其物理背景更符合电力系统特点且可考虑不同发电容量及负荷水平的影响。

节点n的电气介数（electric betweenness）Be(n)定义为

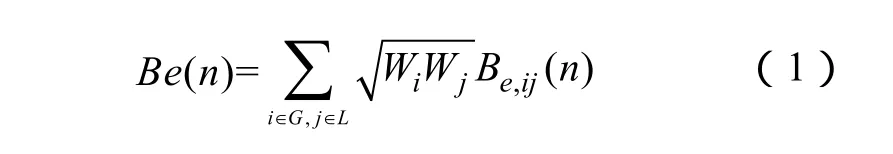
式中，G为发电节点集合；L为负荷节点集合，(i,j)为所有“发电-负荷”节点对；Wi为发电节点的权重，取发电机额定容量或是实际出力；Wj为负荷节点的权重，取实际或峰值负荷；Be,ij(n)为(i,j)间加上单位注入电流元后在节点上产生的电气介数，其表达式为

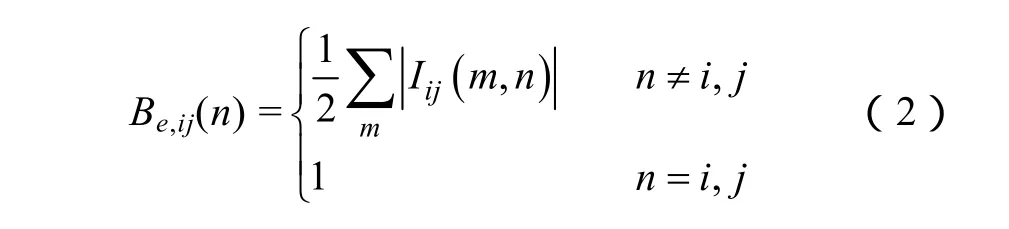
式中，Iij(m,n)为在(i,j)间加上单位注入电流元后在线路(m,n)上引起的电流；m为所有与n有支路直接相连的节点。

式（1）和式（2）中求取 Be(n)的关键是计算Iij(m,n)。为减少计算量，设该系统共有N+1个节点且最后一个为参考节点，则其降阶导纳矩阵为 Y(N×N)。设节点i和参考节点间添加的单位注入电流元为ei，则其在支路上(m,n)上引起的电流为

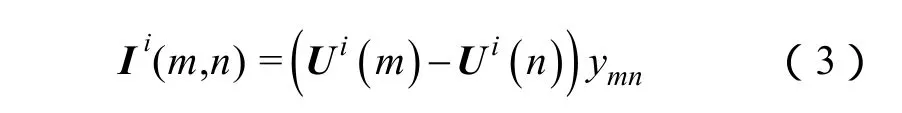
式中，Ui为ei在各节点上所引起的电压组成的向量，并满足 YUi=ei；Ui(m)和 Ui(n)为其在节点 m和 n上的分量；ymn为支路(m,n)的导纳。

若设节点 i和节点 j之间添加的单位注入电流元为eij，则有eij=ei-ej同时根据线性电路的可加性，可得出

Iij(m,n)= Ii(m)-Ij(n) （4）

即 eij在支路(m,n)上所引起的电流等于 ei和 ej在该支路上分别引起的电流的线性和。

故根据式（1）～式（4）计算出节点电气介数，数值越大证明其越关键。结合“一半一半”原则[12]，将节点分为关键节点与一般节点，前50%为关键节点，其余为一般节点。

2.2 可靠性损失指标

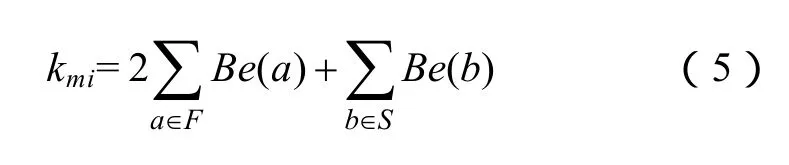
定义1：N个节点中任意一个节点完全丢失数据时，不可观测节点的电气介数加权和表示配置方案在该情况下的可靠性损失指标：式中，kmi为在m配置方案下第i个节点完全丢失数据时的可靠性损失指标，表示节点 i对系统可靠性影响的程度，kmi数值越大，对系统可靠性影响越大；F为关键节点集合；S为一般节点集合；Be(a)、Be(b)为不可观测节点的电气介数。

定义2：m配置方案下，所有节点的可靠性损失指标的均值表示系统的可靠度：

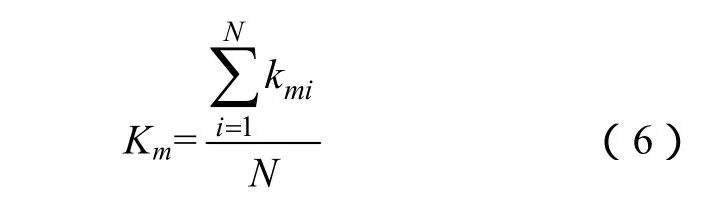
式中，N为系统节点数；Km表示在m配置方案下，任意一个节点完全丢失数据时，系统不可观测的程度，对于同一系统，Km值越小，证明量测配置越好，当Km=0时，系统完全可观，不存在不可观测节点，配置方案良好，无需进行可靠度改进。

3 可观度

可测性的理论和方法具有二值性，即可观或者不可观，系统的可观测性反映的仅仅是系统输出估计状态量的可能性，未能反映系统状态变量估计精度和速度，故需要量化系统的可测性，对系统的可观测程度做出判断。

定义3：系统的可观测程度称为可观度。本文分别应用不同的可观度指标来反应状态估计的精度与速度。

3.1 可观度指标η1

用加权最小二乘法进行状态估计计算，其状态量的估计误差为[13]

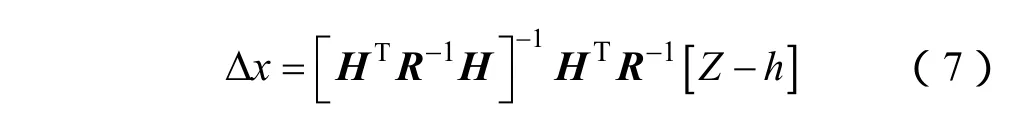
AX=C （8）

状态估计的精度一般反应在估计误差方差阵上，其对角元素表示量测系统可能达到的精度，令

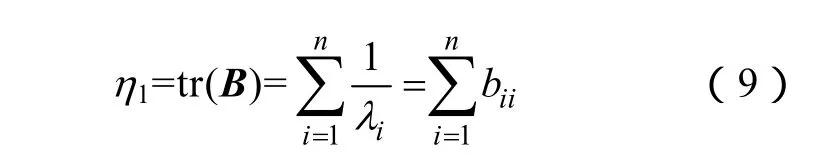
式中，λi是 A 的实特征值，λ1≤λ2≤…≤λn；bii是B的对角元；n=2N-1，N是系统的节点数，η1是可观度的精度指标。

对式（9）进行灵敏度分析：η1的最敏感元与估计误差方差阵的最大对角元maxbii相对应。因而在maxbii对应的节点上增加量测，可以最大限度地降低η1，提高估计精度。某个量测对η1的影响不仅取决于该量测的精度，还取决于网络结构和参数[9]；故根据的排名以及各自所对应的节点增加量测配置，节点排名越靠前对η1的影响越大。

3.2 可观度指标η2

信息矩阵A的谱条件数为

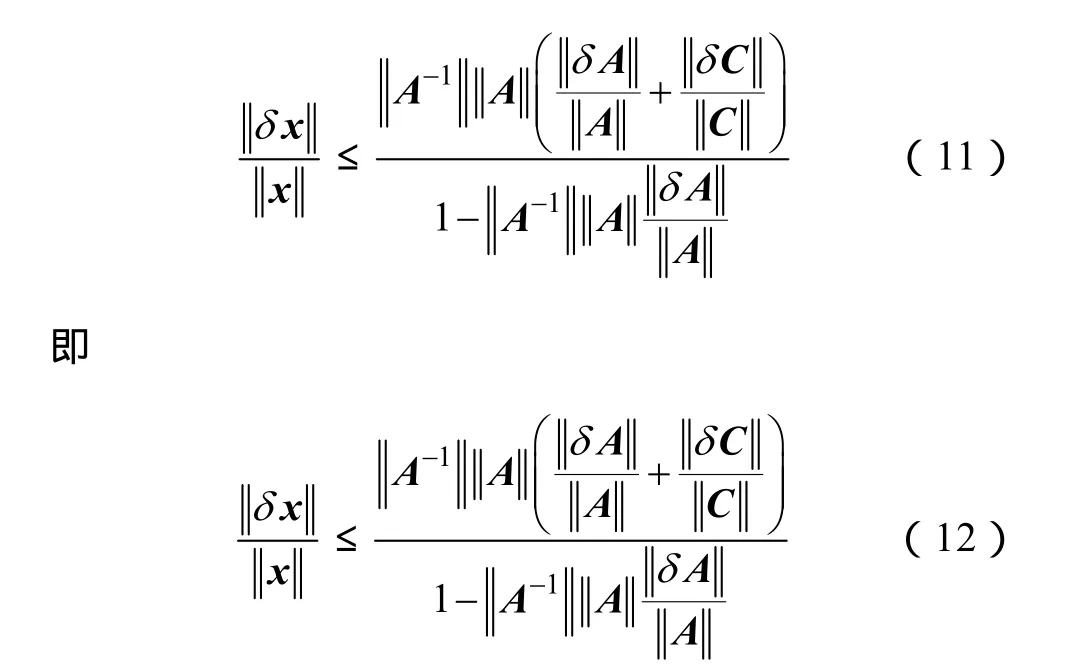
分析式（7），设存在扰动δA，相应地自由矢量C的扰动为δC，解X的扰动为δC，根据文献[14]的式（6）和式（7）可以得到

另外，通过大量的仿真数据与实际工程实践发现，条件数的大小在一定程度上反映了计算速度，条件数小的计算速度比较快，如图1所示，纵轴为计算收敛需要的迭代次数，反应计算速度；横轴为条件数的大小。

结合上述分析，本文将信息矩阵A的谱条件数作为可观度的数值稳定性与速度指标

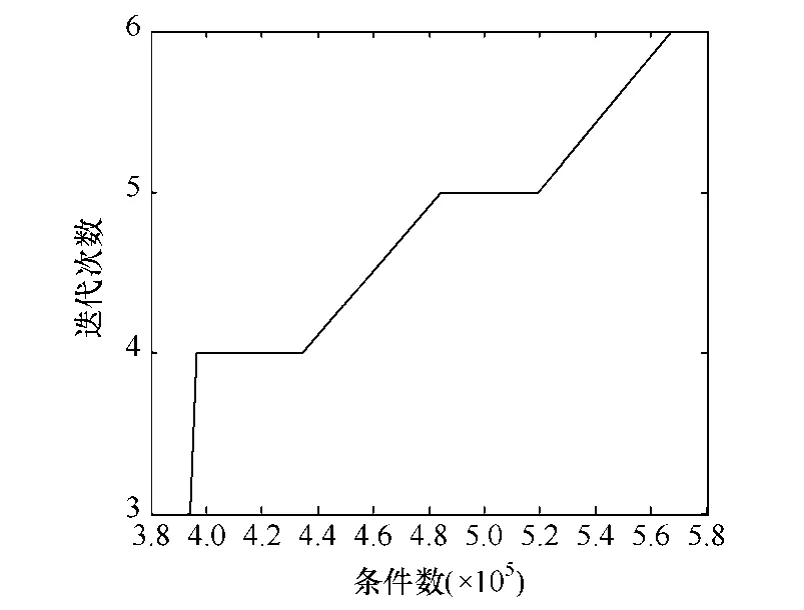
图1 IEEE 14系统的条件数与迭代次数关系图Fig.1 The relational graph of condition number and iterations in IEEE 14 bus system

对式（13）进行灵敏度分析，发现η2的最敏感元与η1最敏感元相同。

4 量侧配置

4.1 量测系统配置优化

对于已配置的量测系统，本文量测优化配置方法步骤如下：

（1）读入原始配置（m=0）数据。

（2）分别进行 N个节点丢失数据实验，依据文献[15]提出的基于量测函数向量线性相关性的可观测性分析数值算法确定每次丢失数据时的不可观测节点，并由式（5）、式（6）计算可靠性损失指标kmi与可靠度Km；确定m配置下的排名及其各自所对应的节点，即可得到各个节点的排名。

（3）判定Km是否为零，若为零，则满足可靠度要求；否则，对量测配置进行改善：根据步骤（2）中不可观测节点与节点排名确定增加量测配置的节点（排名靠前的节点优先配置）；改善完成后，至m=m+1，返回步骤（2），直至Km=0结束可靠度的优化。

（4）可靠度满足要求后，进行可观度优化，至n=0。

（5）分别由式（9）、式（13）计算可观度精度指标η1n与数值稳定性指标η2n。

（6）依据节点排名，对量测配置进行改善：排名靠前的节点优先增加量测配置；改善完成后，至n=n+1，返回步骤（5），当Δη1＜ε1，Δη2＜ε2时，结束可观度的优化。具体优化流程图如图2所示。

图2 量测配置优化流程图Fig.2 Flow chart of measurement configuration optimization

优化配置原则：对于待优化节点 a，增加注入量测或支路量测，优先增加注入量测；增加支路量测时，除去a对端已配置的支路外，所有与a相连的支路均配置。

4.2 量测系统配置规划

对于未配置的量测系统，首先，本文采用注入量测与电压量测，保证在正常情况下，系统可观；在此基础上，增加支路量测，保证任意一个节点完全丢失数据时，系统仍旧完全可观，此量测配置达到可靠性的要求；最后，在此基础上，进行可观度的优化，找到η1与η2最大敏感元所对应的节点，在该节点所连支路侧增加量测配置。

（1）配置N-1个节点注入基量测[15]与参考节点电压Vs，正常情况下，系统满足可观测性的约束条件。

（2）增加支路量测配置，保证任意一个节点完全丢失数据时，系统完全可观。增加的原则：丢失数据实验中kmi取值大的节点优先配置，当kmi=0，Km=0时，停止增加支路量测，m量测配置下满足本文可靠性要求。

按照本文所提方法对量测系统进行配置规划，以较少的量测获得较高的估计精度与数值稳定性且缩短计算时间，并满足可靠性要求。

5 算例仿真

本文采用IEEE 14与IEEE 39节点系统作为测试系统。以IEEE 14系统为例，说明具体的配置过程，以节点1为平衡节点，以潮流计算结果作为系统的运行条件。

5.1 量测系统配置优化

按照 3.1节所述优化步骤，首先，在初始量测配置（m=0）下进行可靠度改善，初始配置见表1。对每个节点 i分别进行丢失数据实验，每次实验不可观测节点为：i、11、14，并由式（5）、式（6）计算k0i与K0，m=0时的节点排名为：12、11、14、13、6、8、3、10、9、7、4、2、1、5，其中节点11、12并列第一；所以在节点 11、14同时增加注入量测配置Q11与P14，实验发现此配置下（m=1）所有节点均可观测，且k1i=0，K1=0，优化结束。实验过程中发现当仅在节点11增加量测配置时，每次丢失数据实验不可观测节点为：i、14；当仅在节点14增加量测配置时，每次丢失数据不可观测节点为：i、11；所以在节点 11、14同时增加量测配置没有造成资源浪费，保证了经济上的最优；具体优化过程数据见表2与表3。

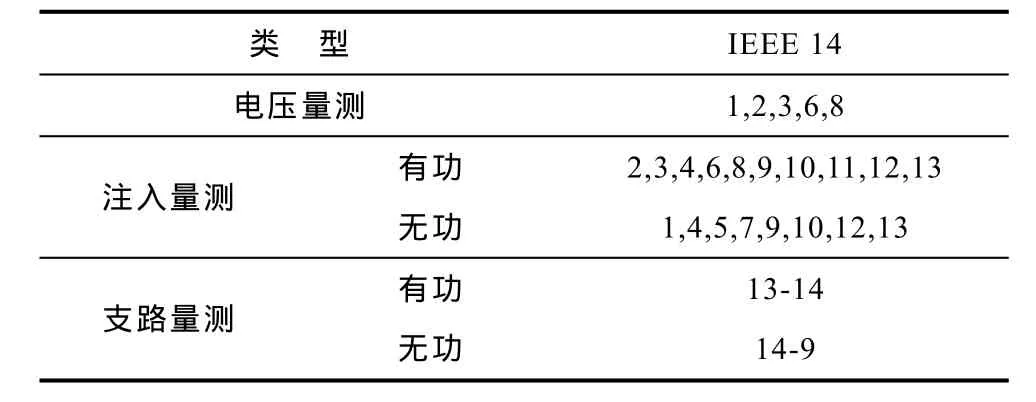
表1 IEEE 14节点系统的量测初始配置Tab.1 The initial measurement configuration of IEEE 14 bus system

表2 IEEE 14节点系统丢失数据实验结果Tab.2 Missing data experimental results of IEEE 14 bus system

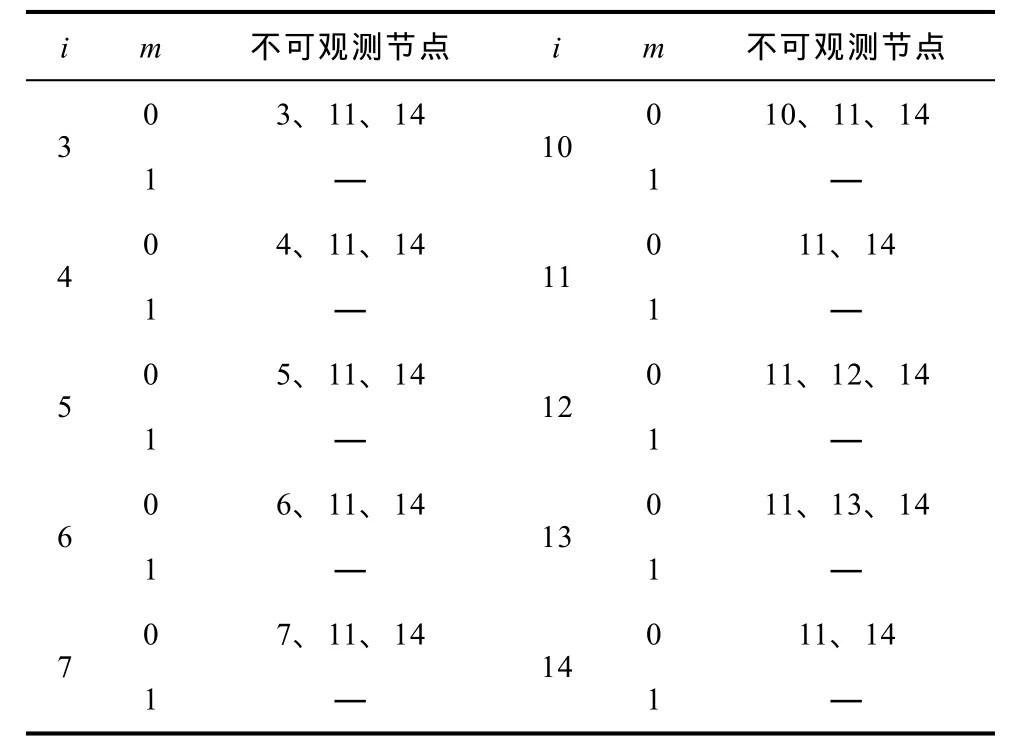
（续）

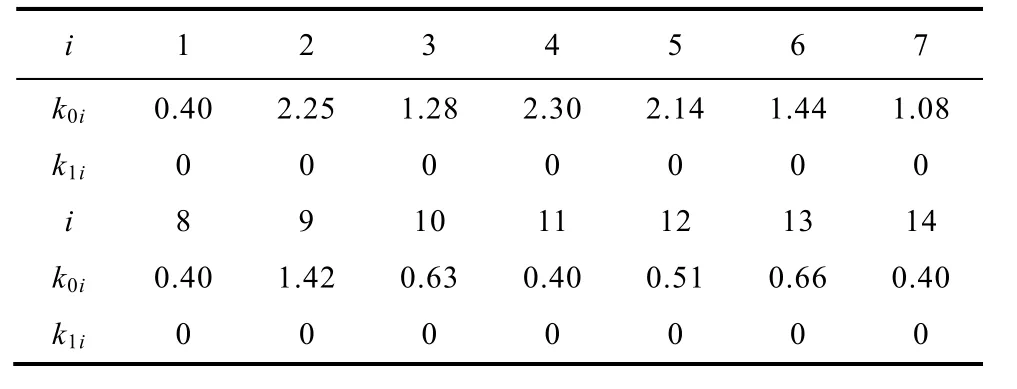
表3 IEEE 14节点系统kmi的改善记录Tab.3 The improved record of kmi in IEEE 14 bus system

其次，在可靠度优化完成后的量测配置下进行可观度优化。n=0（m=1）时的节点排名为：8、6、3、12、13、11、14、10、9、7、2、1、4、5。按照上述顺序按照配置原则依次增加量测，图4与图 5分别展现了IEEE 14节点系统的精度指标与数值稳定性指标的改善过程。由图4与图5可见第4次与第3次的改善效果相差甚微，所以依次在节点8、6、3安装量测配置（Q8,Q6,Q3）即完成η1与η2的优化，可观度得到最大限度的改善，使系统具有精确的估计结果与良好的数值稳定性。

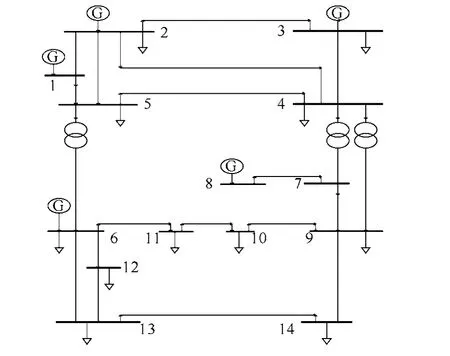
图3 IEEE 14节点系统Fig.3 IEEE 14 bus system

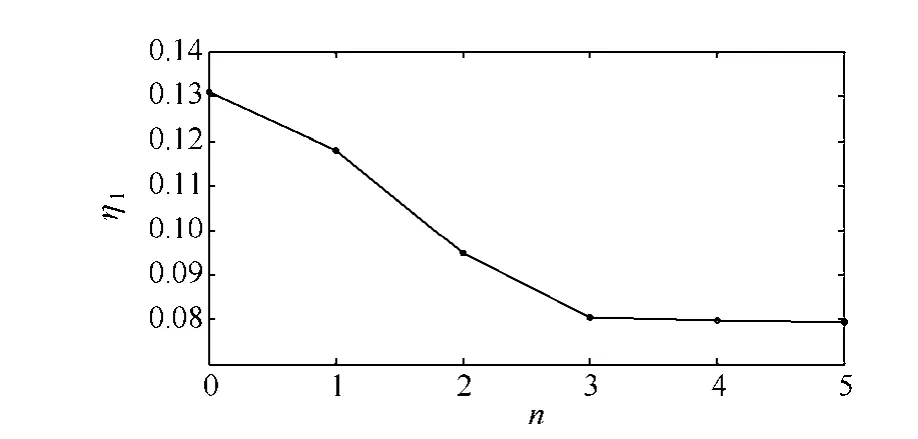
图4 IEEE 14节点系统η1改善过程Fig.4 The improvement process of η1 in IEEE 14 bus system

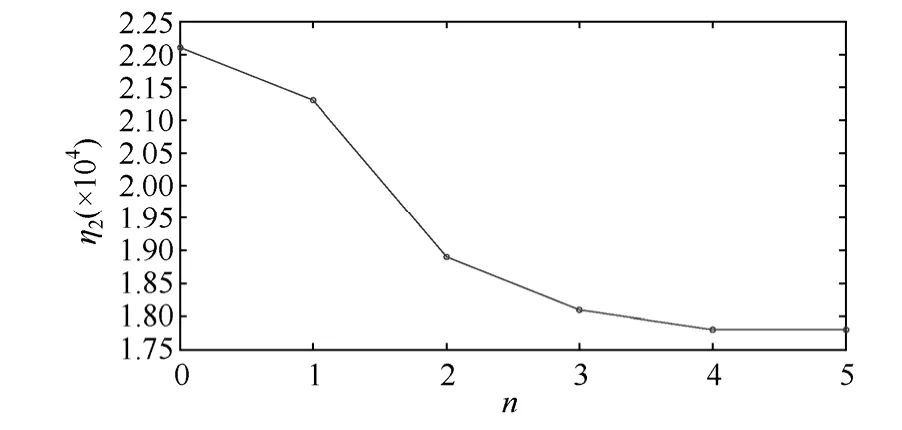
图5 IEEE 14节点系统η2改善过程Fig.5 The improvement process of η2 in IEEE 14 bus system

综合上述仿真分析，对IEEE 14系统初始量测配置进行改善，在节点11、14增加量测，完成可靠度的改善，保证任意一个节点完全丢失数据时系统仍旧完全可观测；在此基础上，在节点8、6、3增加量测，完成可观度改善，使状态估计的精度、速度与数值稳定性均得了最大限度的改善。

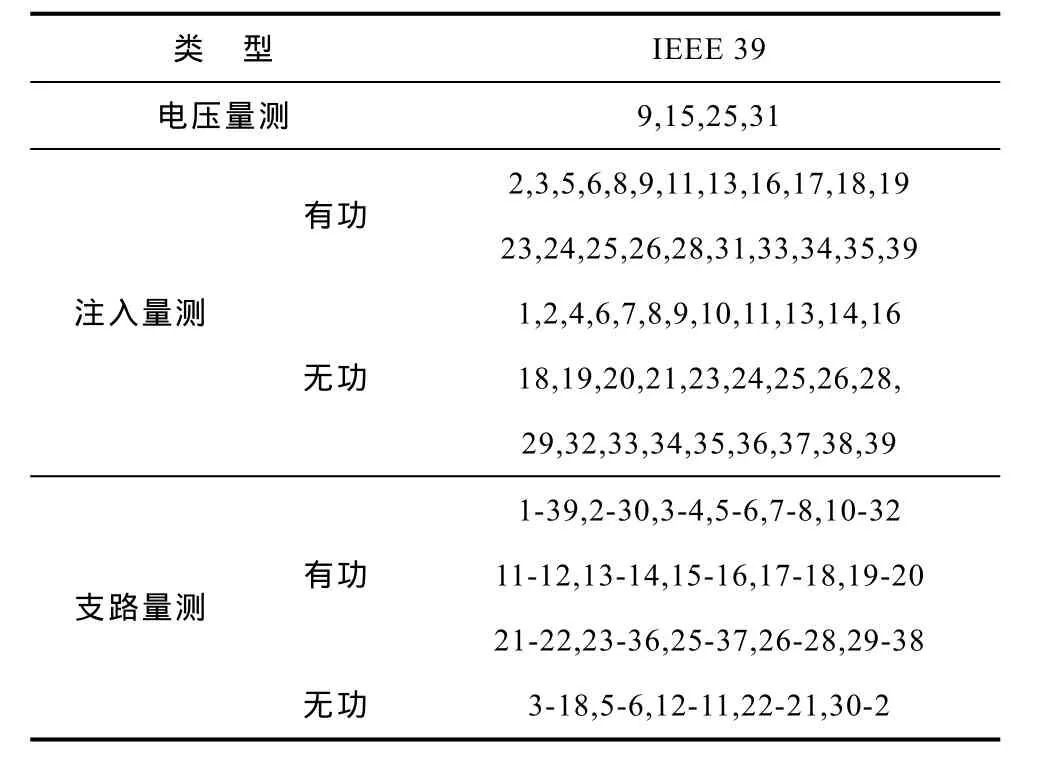
表4 IEEE 39节点系统的量测初始配置Tab.4 The initial measurement configuration of IEEE 39 bus system

IEEE 39节点系统初始量测配置（m=0）见表4，此量测系统详尽的改善过程不再赘述，在m=0时，增加量测P32与Q30；m=1，增加量测P10与P14；m=2时，增加量测Q12。此时，kmi=0，Km=0，系统的可靠度优化结束。表 5列出了 IEEE14、39节点系统在可靠度改善过程中K的变化。

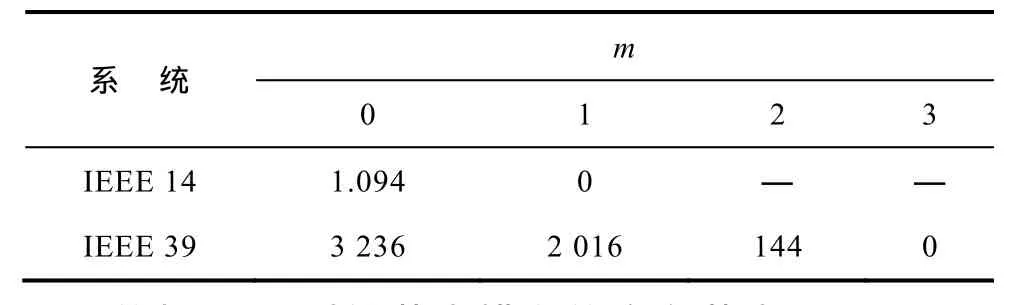
表5 IEEE 14/39节点系统K的改善记录Tab.5 The improved record of K in IEEE 14/39 bus system

依据m=3时的节点排名依次在节点28、3、38增加量测配置（P28*,Q3,P38），图 6与图7分别展现了IEEE 39节点系统的精度指标与数值稳定性指标的改善过程。由图6与图7可见第2次与第3次的改善效果相差甚微，因此，在节点28、3增加量测配置即可。

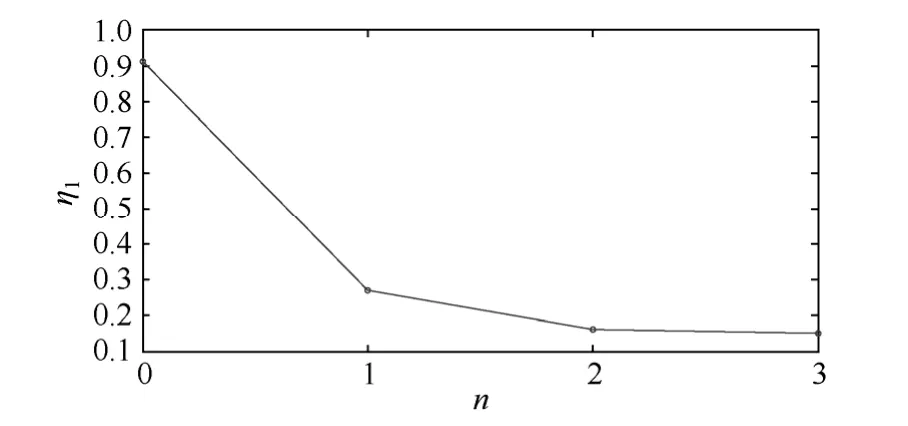
图6 IEEE 39节点系统η1改善过程Fig.6 The improvement process of η1 in IEEE 39 bus system

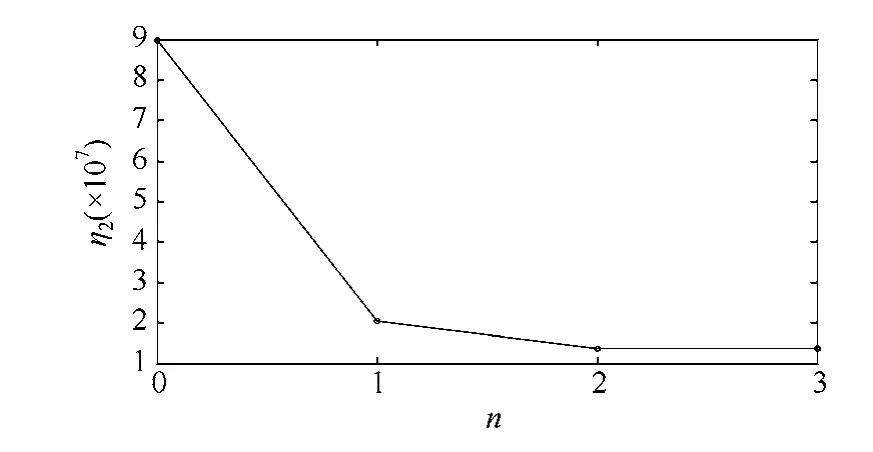
图7 IEEE 39节点系统η2改善过程Fig.7 The improvement process of η2 in IEEE 39 bus system

综上所述，在节点 3、10、12、14、28、30、32增加量测配置，即可完成系统可靠度与可观度的改善。

5.2 量测系统配置规划

按照3.2节所述配置步骤，首先，在节点2～14配置节点注入基量测，同时配置参考节点电压V1；在此量测配置（m=0）下，进行N次丢失数据实验，每次试验不可观测节点为 i，各个节点可靠性损失指标的排序为：4、2、5、6、9、3、7、1、13、10、11、14、12、8；其次，在节点 4侧配置支路量测（m=1），重复上述实验，可知k1,4≠0且与节点4相连的节点中节点2的电气介数最大，故在节点2处配置支路量测（m=2），此时 k2i=0，K2=0，完成可靠度配置；最后，依据最终可靠度配置（n=0(m=2)）下的的节点排名顺序：6、14、3、12、13、11、9、10、7、8、4、5、2、1依次配置支路量测，由图1可知，在节点 6配置（n=1）即可完成可观度的配置，最终配置后的可观测情况见表 2。在配置过程中有功无功量测同时配置。表6记录了IEEE 14节点系统在配置过程中η1与η2的变化情况。IEEE 14/39节点系统最终量测配置见表7。

表6 IEEE 14节点系统配置过程中η1与η2变化记录Tab.6 The record of η1 and η2 in IEEE 14 bus system during measurement configuration process

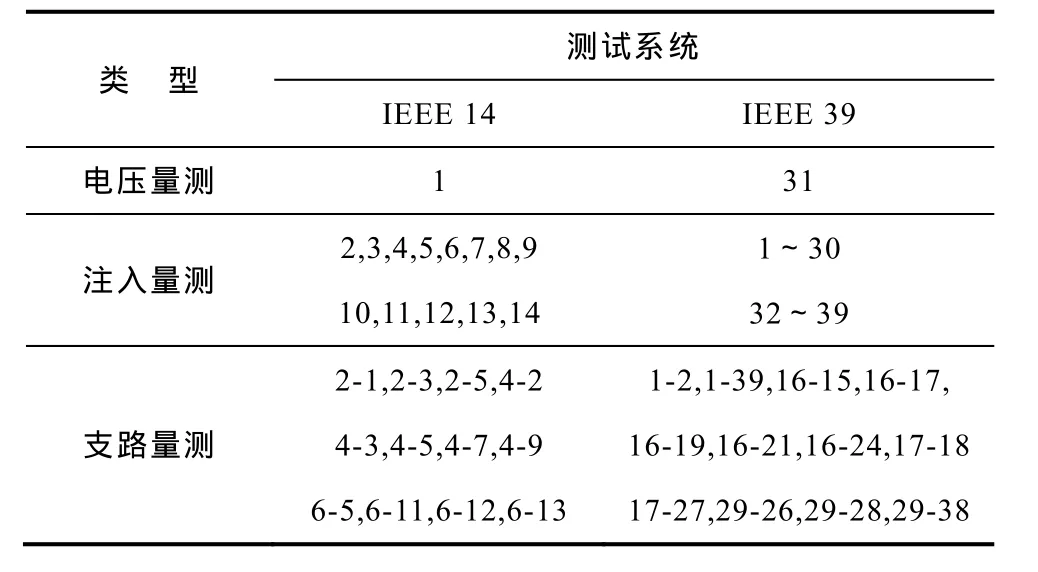
表7 IEEE14/39节点系统最终量测配置Tab.7 The last measurement configuration in IEEE14/39 bus system

6 结论

本文提出了可靠度和可观度概念，并在此基础上设计了一种量测系统优化与配置的方法，算例仿真结果表明：该方法在测量系统配置优化方面不仅能够保证系统在任意一个节点完全丢失数据的情况下仍旧完全可观，而且还可以保证良好的数值稳定性与精确的估计结果；测量系统配置规划可以有效提高系统的可靠度和可观度。考虑到实际电网数据量大、结构复杂等原因，在进一步研究中将用实际算例进行测试，以使得本方法得到实际应用。

[1] 卢志刚, 李爽. 厂站量测信息不完整时的全网理论线损计算[J]. 电网技术, 2007, 31(16): 83-87.Lu Zhigang, Li Shuang. Theoretical network loss calculation of whole power system under incomplete injected measured data of partial plants and substations[J]. Power System Technology, 2007, 31(16): 83-87.

[2] Milosevic B, Begovic M. Nondominated sorting genetic algorithm for optimal phasor measurement placement[J]. IEEE Transactions on Power Systems,2003, 18(1): 69-75.

[3] Nuqui R F, Phadke A G. Phasor measurement unit placement techniques for complete and incomplete observablity[J]. IEEE Transactions on Power Delivery,2005, 20(4), 2381-2388.

[4] 彭疆南, 孙元章, 王海风. 考虑系统完全可观测性的 PMU最优配置方法[J]. 电力系统自动化. 2003,27(4): 10-16.Peng Jiangnan, Sun Yuanzhang, Wang Haifeng. An optimal PMU placement algorithm for full network observability[J]. Automation of Electric Power Systems,2003, 27(4): 10-16.

[5] 李川江, 邱国跃. 基于改进粒子群算法的PMU装置数量增加过程中的最优配置方法[J]. 继电器, 2006,34(12): 52-56, 68.Li Chuanjiang, Qiu Guoyue. Optimal placement algorithm of PMU based on enhanced particle swarm optimization during the increase of PMUs[J]. Relay,2006, 34(12): 52-56, 68.

[6] Denegri G B, Invernizzi M, Milano F. A security oriented approach to PMU positioning for advanced monitoring of a transmission grid[C]. International Conference on Power System Technology, Kunming,China, 2002.

[7] 刘新东, 江全元, 曹一家. N-1条件下不失去可观测性的 PMU优化配置方法[J]. 中国电机工程学报,2009, 29(10): 47-51.Liu Xindong, Jiang Quanyuan, Cao Yijia. Optimal PMU placement to guarantee observability under N-1 condition[J]. Proceedings of the CSEE, 2009, 29(10):47-51.

[8] 陈刚, 唐毅, 张继红, 等. 基于田口法考虑N-1情况下的PMU优化配置方法[J]. 电力系统自动化, 2010,34(13): 28-32.Chen Gang, Tang Yi, Zhang Jihong, et al. Optimal PMU placement based on taguchi method considering N-1 condition[J]. Automation of Electric Power Systems, 2010, 34(13): 28-32.

[9] 王克英, 穆钢, 陈学允. 计及PMU的状态估计精度分析及配置研究[J]. 中国电机工程学报, 2001,21(8): 29-33.Wang Keying, Mu Gang, Chen Xueyun. Precision improvement and PMU placement studies on state estimation of a hybrid measurement system with PMUS[J]. Proceedings of the CSEE, 2001, 21(8):29-33.

[10] 徐林, 王秀丽, 王锡凡. 电气介数及其在电力系统关键线路识别中的应用[J]. 中国电机工程学报,2010, 30(1): 33-39.Xu Lin, Wang Xiuli, Wang Xifan. Electric betweenness and its application in vulnerable line identification in power system[J]. Proceedings of the CSEE, 2001,21(8): 29-33.

[11] 徐林, 王秀丽, 王锡凡. 基于电气介数的电网连锁故障传播机制与积极防御[J]. 中国电机工程学报,2010, 30(13): 61-68.Xu Lin, Wang Xiuli, Wang Xifan. Cascading failure mechanism in power grid based on electric betweenness and active defence[J]. Proceedings of the CSEE, 2010,30(13): 61-68.

[12] Taguchi G, Chowdhury S, Taguchi S. Robust engineering[M]. New York, NY, USA: McGraw-Hill, 2000.

[13] 于尔铿. 电力系统状态估计[M]. 北京: 水利电力出版社, 1985.

[14] 李庆阳, 王能超, 易大义. 数值分析[M]. 北京: 华中理工大学出版社, 2000.

[15] 卢志刚, 张宗伟. 基于量测函数向量线性相关的网络可观测性分析[J]. 电网技术, 2007, 31(17): 51-55.Lu Zhigang, Zhang Zongwei. Network observability analysis based on linear dependence between measurement function vectors[J]. Power System Technology,2007, 31(17): 51-55.