矩形截面大偏心受压构件对称配筋与非对称配筋钢筋用量对比的分析研究

谢立安

（山西省交通科学研究院 桥梁工程防灾减灾山西省重点实验室黄土地区公路建设与养护技术交通行业重点实验室，山西 太原 030006）

0 引言

矩形截面大偏心受压构件配筋设计分为非对称配筋设计和对称配筋设计两种情况。若受压构件两侧钢筋面积As≠A's时，则称为非对称配筋；若受压构件两侧钢筋面积As=A's、抗拉抗压强度fy=f'y且as=a′s时，则称为对称配筋[1-2]。采用非对称配筋可节约钢筋用量，但施工不便；实际工程设计中，若受压构件可能承受正负两方向弯矩，或为使构造简单及便于施工时，常采用对称配筋[1-2]。然而对称配筋钢筋总用量始终不少于非对称配筋，但具体增加量均未提及。为此，本文运用具体算例、直观分析和理论分析，得出矩形截面大偏心受压构件对称配筋相对于非对称配筋时受压钢筋A's增加量、受拉钢筋As增加量和钢筋总用量A's+As增加量的计算公式，以及钢筋增加量与轴向压力N和初始偏心距ei的相关关系，研究成果可为工程设计人员提供参考依据。

1 具体算例

某矩形截面大偏心受压构件，截面尺寸为b×h=400 mm×600 mm，混凝土强度等级为C30混凝土（fc=14.3 N/mm2，α1=1.0），纵向钢筋为 HRB400 级钢筋（fy=f'y=360 N/mm2，ξb=0.518），受拉和受压钢筋合力点至混凝土近表面距离为as=a's=400 mm，截面有效高度h0=560 mm，控制截面上轴向压力设计值N从N=250 kN逐级增大到N=1 500 kN，初始偏心距ei从ei=0.4h0逐级增大到ei=1.5 h0，现求解对称配筋相对于非对称配筋时受压钢筋A's增加量、受拉钢筋As增加量及钢筋总用量A's+As增加量。结果如表1～表3所示。

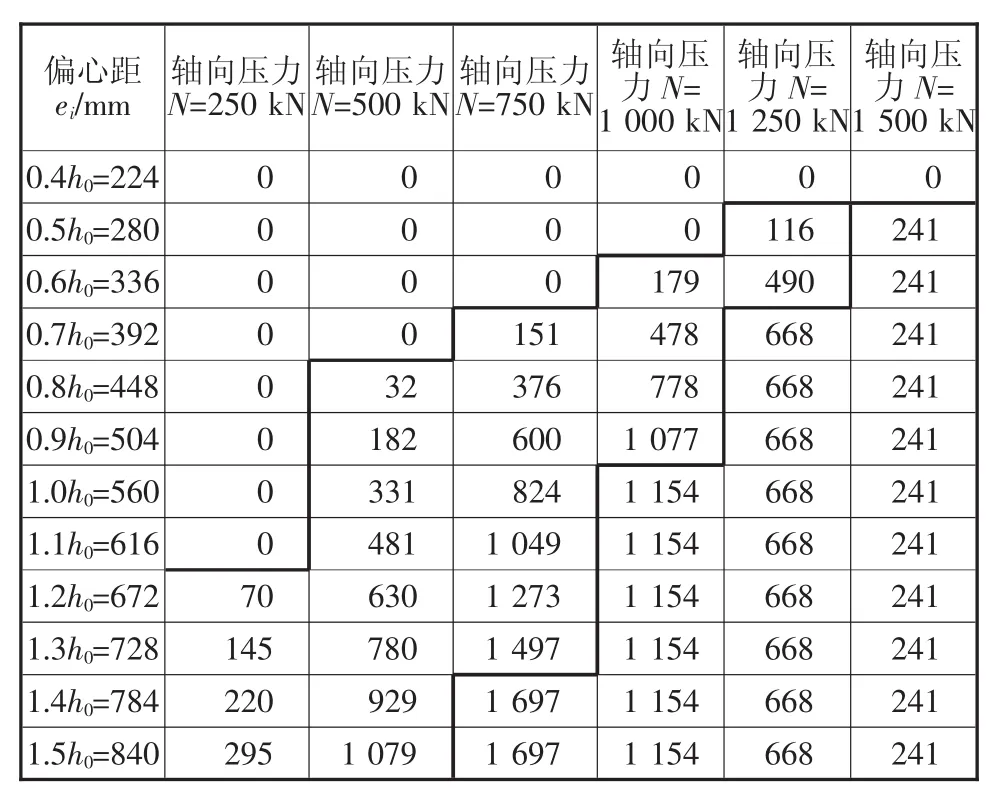
表1 对称配筋相对于非对称配筋时受压钢筋As’增加量结果表

表2 对称配筋相对于非对称配筋时受拉钢筋As增加量结果表

2.表1～表3中间区为非对称配筋受压钢筋A′s计算结果小于最小配筋面积，但非对称配筋受拉钢筋As和对称配筋受压钢筋A′s及受拉钢筋As计算结果均大于最小配筋面积的区域。

3.表1～表3右下区为非对称配筋和对称配筋受压钢筋A′s及受拉钢筋As计算结果均大于最小配筋面积的区域。

4.表3中百分比为对称配筋相对于非对称配筋时钢筋总用量增加的百分比。

由表1～表3可得，对称配筋相对于非对称配筋时受压钢筋增加量、受拉钢筋增加量及钢筋总用量增加量与轴向压力和初始偏心距的相关关系，如图1～图3所示。

图1 对称配筋相对于非对称配筋时受压钢筋As’增加量图

图2 对称配筋相对于非对称配筋时受拉钢筋As增加量图

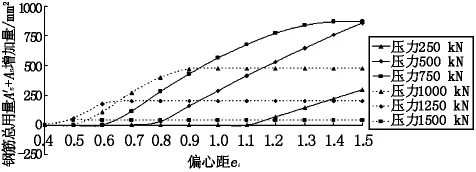
图3 对称配筋相对于非对称配筋时钢筋总用量 As’+As增加量图

由表1～表3和图1～图3可得：

a）当初始偏心距ei较小时，对称配筋和非对称配筋受压钢筋A's及受拉钢筋As的计算结果均小于最小配筋面积，因此均应取最小配筋面积。此时对称配筋和非对称配筋受压钢筋A's及受拉钢筋As用量相等，钢筋总用量A's+As也相等。

b）当初始偏心距ei稍大时，对称配筋受压钢筋A's的计算结果开始大于最小配筋面积，而非对称配筋受压钢筋A's的计算结果依然小于最小配筋面积，应取最小配筋面积；对称配筋和非对称配筋受拉钢筋As的计算结果同时大于最小配筋面积，但对称配筋受拉钢筋As用量相对于非对称配筋受拉钢筋As用量增长较慢。此时对称配筋受压钢筋A's用量开始大于非对称配筋受压钢筋A's用量，对称配筋受拉钢筋As用量开始小于非对称配筋受拉钢筋As用量，对称配筋钢筋总用量A's+As开始大于非对称配筋钢筋总用量A's+As。

c）当初始偏心距ei继续增大时，非对称配筋受压钢筋A's的计算结果也开始大于最小配筋面积，此时对称配筋受压钢筋A's用量始终大于非对称配筋受压钢筋A's用量，对称配筋受拉钢筋As用量始终小于非对称配筋受拉钢筋As用量，对称配筋钢筋总用量A's+As始终大于非对称配筋钢筋总用量A's+As。然而当对称配筋和非对称配筋受压钢筋及A's受拉钢筋As的计算结果均大于最小配筋面积时，对称配筋相对于非对称配筋时受压钢筋A's增加量、受拉钢筋As减少量和钢筋总用量A's+As增加量均为定值，且均与初始偏心距ei无关，但随轴向压力N的增大而减小。

d）当轴向压力N和初始偏心距ei均较小时（表3左上区），对称配筋和非对称配筋钢筋总用量A's+As相等；当轴向压力N较小且初始偏心距ei较大或轴向压力N较大且初始偏心距ei较小时（表3中间区），对称配筋相对于非对称配筋时钢筋总用量A's+As增加的百分比随初始偏心距ei的增大而增大，最大为38%；当轴向压力N和初始偏心距ei均较大时（表3右下区），对称配筋相对于非对称配筋时钢筋总用量A's+As增加的百分比均随轴向压力N和初始偏心距ei的增大而减小，最大为25%，最小趋于0%。因此实际工程设计中，当轴向压力N和初始偏心距ei均较小或较大时，为计算和施工方便并适当增加结构的安全性，非对称配筋完全可以按对称配筋来进行设计。

2 直观分析

对于受压钢筋A's，由于非对称配筋相对于对称配筋时更充分利用了混凝土的承载力（表现为受压钢筋A's求解公式中取x=ξbh0作为设计补充条件），即对称配筋相对于非对称配筋时受压区混凝土高度减小，致使对称配筋相对于非对称配筋时受压区混凝土承担了较小的轴向压力，因此在承受相同轴向压力N时，对称配筋相对于非对称配筋时受压钢筋A's用量增加。

对于受拉钢筋As，由于非对称配筋相对于对称配筋时更充分利用了混凝土的承载力（表现为受压钢筋A's求解公式中取x=ξbh0作为设计补充条件），即对称配筋相对于非对称配筋时受压区混凝土高度减小，致使对称配筋相对于非对称配筋时受拉钢筋内力臂（即受拉钢筋合力点至受压区混凝土和受压钢筋合力点的距离）增加，因此在承受相同弯矩Ne时，对称配筋相对于非对称配筋时受拉钢筋As用量减小。

3 理论分析

在满足矩形截面大偏心受压构件配筋设计基本公式适用条件下，对称配筋相对于非对称配筋时受压钢筋A's增加量、受拉钢筋As增加量和钢筋总用量A's+As增加量可表达为：

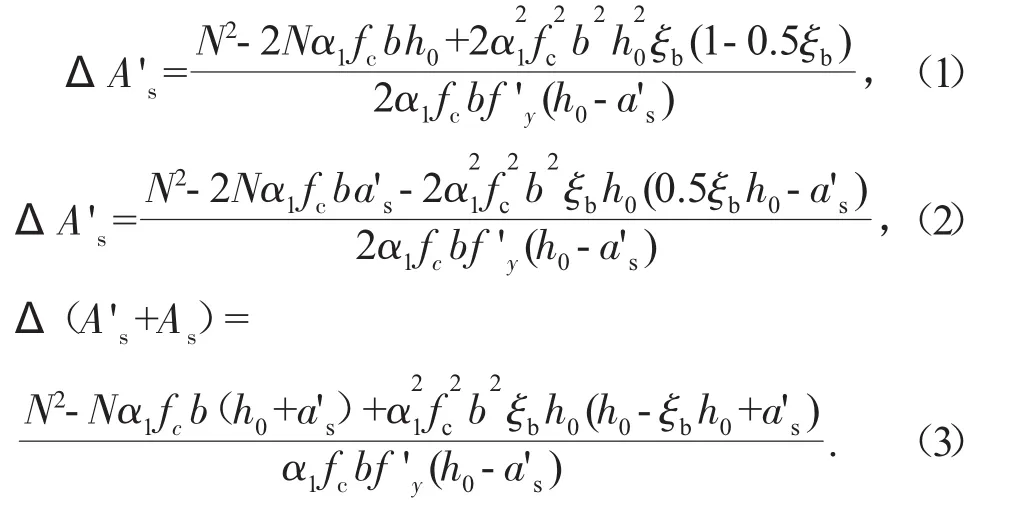
由公式（1）、公式（2）和公式（3）可以看出，受压钢筋A's增加量、受拉钢筋As增加量和钢筋总用量A's+As增加量均与轴向压力N呈二次抛物线函数关系，而均与初始偏心距ei无关，表明在满足矩形截面大偏心受压构件配筋设计基本公式适用条件且轴向压力N不变的情况下，受压钢筋A's增加量、受拉钢筋As增加量和钢筋总用量A's+As增加量均为定值，且均与初始偏心距ei无关，这与表1～表3的计算结果及图1～图3的显示结果完全一致。

将上述具体算例的数据代入公式（1）、公式（2）和公式（3），在满足矩形截面大偏心受压构件配筋设计基本公式适用条件下，取轴向压力设计值N从N=750 kN逐级增大到N=1 500 kN，可得对称配筋相对于非对称配筋时受压钢筋增加量A's受拉钢筋As增加量和钢筋总用量A's+As增加量如表4所示。

表4 对称配筋相对于非对称配筋时钢筋增加量结果表

由表4可得，在满足矩形截面大偏心受压构件配筋设计基本公式适用条件下，公式（1）、公式（2）和公式（3）的计算结果与表1～表3的计算结果非常吻合，为此，公式（1）、公式（2）和公式（3）可作为矩形截面大偏心受压构件对称配筋相对于非对称配筋时受压钢筋A's增加量、受拉钢筋As增加量和钢筋总用量A's+A's增加量的计算公式。

4 结论

a）在满足矩形截面大偏心受压构件配筋设计基本公式适用条件下，对称配筋相对于非对称配筋时受压钢筋增加量、受拉钢筋增加量和钢筋总用量增加量的计算公式如公式（1）、公式（2）和公式（3）所示，且受压钢筋增加量、受拉钢筋增加量和钢筋总用量增加量均与轴向压力呈二次抛物线函数关系，而均与初始偏心距无关。

b）当受压钢筋面积和受拉钢筋面积均大于最小配筋面积时，若轴向压力不变，则对称配筋相对于非对称配筋时受压钢筋增加量、受拉钢筋增加量和钢筋总用量增加量均为定值，且均与初始偏心距无关；当偏心距较大且不变时，对称配筋相对于非对称配筋时受压钢筋增加量、受拉钢筋增加量和钢筋总用量增加量均随轴向压力的增大而减小。

c）相同条件下，对称配筋钢筋总用量始终不少于非对称配筋钢筋总用量。当轴向压力和初始偏心距均较小时，对称配筋和非对称配筋钢筋总用量相等；当轴向压力较小且初始偏心距较大或轴向压力较大且初始偏心距较小时，钢筋总用量增加量最大为38%；当轴向压力和初始偏心距均较大时，钢筋总用量增加量最大为25%，最小趋于0%。因此实际工程设计中，当轴向压力和初始偏心距均较小或较大时，为计算和施工方便并适当增加结构的安全性，非对称配筋完全可以按对称配筋来进行设计。