一种基于锥优化的DG优化配置快速计算方法

赵金利 于莹莹 李 鹏 孙充勃 张 楠 郭小龙 张 飞

（1. 天津大学智能电网教育部重点实验室 天津 300072 2. 广东电网公司 广州 510000）

1 引言

在能源需求与环境保护的双重压力下，学术界和工业界已将更多希望寄托于分布式发电相关的研究与解决方案[1]。随着相关政策的推出、实施以及技术水平的不断进步，分布式发电技术目前已得到广泛应用。然而，分布式电源类型丰富、形式多样（如风力发电、光伏发电、燃料电池、微型燃气轮机和内燃机等[2-4]），且其运行特性依据其结构组成、控制模式和技术特点而不同。因此，分布式电源的并网运行对配电系统的安全性、供电可靠性、经济性及电能质量等具有重要影响，而这与分布式电源的接入位置和容量配置紧密相关[4,5]。因此，对分布式电源进行合理的规划，不仅能充分发挥分布式电源的作用和经济效益，还可有效减少分布式电源接入所带来的问题和风险。

分布式电源优化配置问题是指在满足给定的投资及系统运行等约束条件下，对DG的选址和容量进行优化，使其效益最大化。国内外学者从不同角度对DG优化配置问题的计算模型和求解方法进行了研究。文献[6]利用电压灵敏度方法选择DG接入位置，提出一种DG优化配置方法来提高电压稳定域，并考虑了负荷和DG的随机特性。文献[7]以系统无功损耗最小为目标，采用粒子群算法对DG进行优化配置来增强系统的带载能力，提高系统电压稳定性。文献[8]利用蒙特卡罗法考虑负荷和DG的随机特性，力图实现DG接入给供电公司和客户带来的效益最大化。

DG优化问题求解的速度和准确度是目前的研究重点之一。求解算法分为数学微分优化技术[6]、启发式算法[10]、人工智能优化方法[12]等。数学微分优化技术一般仅能实现单个分布式电源的优化配置，启发式算法及人工智能优化方法需调用大量潮流结果来验证DG配置方案的合理性[10-14]，尤其当配电网规模较大时，其计算压力将更为突出，并且解的最优性往往取决于初始点和控制参数的选择。为此，本文选取锥优化方法来求解DG优化配置问题。该方法可实现优化问题和潮流计算问题的统一求解，大大提高了计算速度，且利用严格的数学理论进行建模，保证了解的最优性。

本文首先从分布式电源优化配置的基本模型出发，考虑了配电系统自身的运行要求和分布式电源的接入限制等约束。然后，以锥优化的标准形式为指导，通过变量替换和形式变换实现了优化配置模型向锥约束的转化，建立了分布式电源优化定容的锥优化模型。最后，在IEEE 33节点算例上，分别针对不同的DG接入情况，对锥优化模型转化方法的正确性和计算效率进行测试，并与模式搜索法（Pattern Search，PS）和模拟退火法（Simulated Annealing，SA）进行比较，同时对优化结果进行分析。

2 分布式电源优化定容问题

本文基于现有的DG优化配置模型[6-14,18-21]，从配电系统经济运行的角度出发，建立相应的数学模型。

2.1 目标函数

分布式电源优化配置问题通常根据不同的应用背景选取相应的目标函数，如系统有功损耗最小[9]、系统无功损耗最小[7]、提高电压稳定裕度[6]、环境效益最大等[4]，由于网络损耗的改善情况能有效反应DG安装前后的节能效益和能源利用率，可更好的与电力系统运行的经济性联系起来，因此本文选取系统有功损耗最小化为目标函数，可表示为

式中，n为系统节点数；Pi为节点i处注入的有功功率之和，可用式（2）表示。

2.2 约束条件

约束条件包括系统潮流约束、运行电压水平约束、支路电流限制、DG容量约束、渗透率约束、DG无功出力限制及功率因数限制[6-14,18-21]，具体公式如下。

系统潮流约束

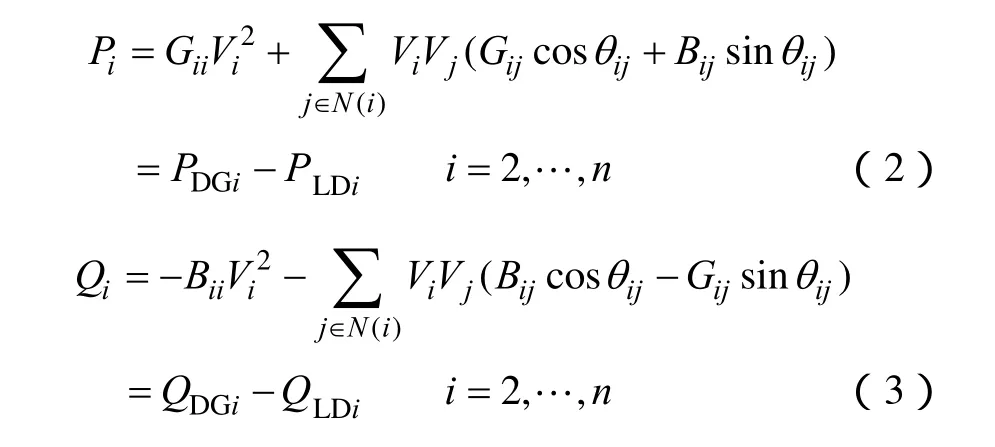
运行电压水平约束

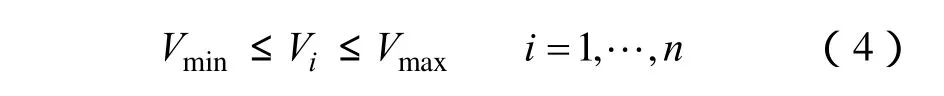
支路电流限制

式中，N(i)为节点i的相邻节点的集合；Vi、Vj、θij分别为节点 i、j的电压幅值和相角差；Gii、Bii、Gij、Bij分别为节点导纳矩阵中的自电导、自电纳、互电导和互电纳；PDGi、PLDi分别为节点i上分布式电源注入的有功功率、负荷注入的有功功率；Qi为节点i处注入的无功功率之和；QDGi、QLDi分别为节点 i上分布式电源注入的无功功率、负荷注入的无功功率；Vmax、Vmin分别为系统i电压幅值的上、下限；Iij为支路ij的电流幅值；Iijmax为支路ij的电流幅值上限；SDGimax为节点 i处分布式电源接入容量的上限；λ为渗透率水平系数；SLD为系统总负荷；pfDGi为节点 i处分布式电源的功率因数；pfmax、pfmin分别为系统中各分布式电源功率因数的上、下限。

式（1）～式（9）构成了以分布式电源出力PDGi、QDGi为决策变量的DG优化定容问题的基本模型。

3 锥优化算法的应用

锥优化是线性优化的一种推广[15]，因凸锥所具有的优美的几何结构和特殊的处理方式，使其不仅能在有效时间内实现问题的求解，还能保证所求解的最优性。在电力系统领域中，锥优化已成功应用于传统配网重构[16]及系统运行状态[17]的求解等。

在传统DG优化配置求解方法中，数学微分优化技术的计算量较小，但一般仅能实现单个DG的优化配置。启发式算法和人工智能算法主要通过调用潮流结果来反复修正DG的接入容量，往往需要足够多的计算次数才能寻得较好的解[10]。与之相比，锥优化算法在求解DG优化配置问题时，能够同时满足快速收敛和最优求解的要求。

3.1 锥优化的标准形式

锥优化是线性空间中凸锥上的数学规划，它是线性规划与非线性规划的推广。锥优化问题可描述为在有限个非空尖凸锥的笛卡尔乘积与仿射子空间的交集上求一个线性目标函数最小的问题，即在非空尖凸锥导入偏序下，线性等式、线性不等式约束条件下的线性目标函数的问题，其标准形式如下

min{cTx|Ax=b, x≥K0} （10）

式中，K为有限个非空尖凸锥的笛卡尔乘积，一般用旋转锥表示，如式（12）；x为n维决策变量。

锥优化方法对优化问题的数学模型有严格要求，锥优化的目标函数必须是决策变量x的线性函数，且其可行域由线性等式/不等式约束和非线性二阶锥或旋转锥不等式约束构成，第一项 Ax=b表示线性约束，第二项x≥K0表示非线性约束。

3.2 锥模型的转化

3.2.1 基本约束条件的锥转化

上述分布式电源优化定容模型属于非线性规划，应用锥优化算法进行求解时，需根据锥优化的标准形式对模型做相应的变换处理，使之满足对于线性目标函数和凸锥搜索空间的要求。首先，根据式（2）的数学描述，通过变量替换的方式实现目标函数（1）的线性化，即利用 Xi、Yij、Zij将优化定容模型中 Vi、Vj、θij乘积的非线性形式进行变量替换[16]

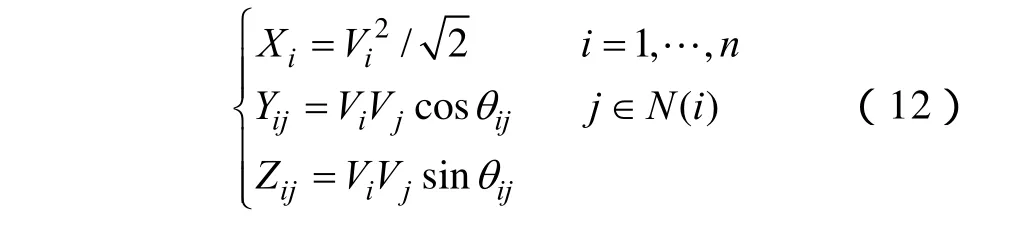
变量替换后，非线性目标函数（1）变换为如式（13）所示的线性形式。

与此同时，含 Vi、Vj、θij的约束条件（2）～（5）相应地变换为

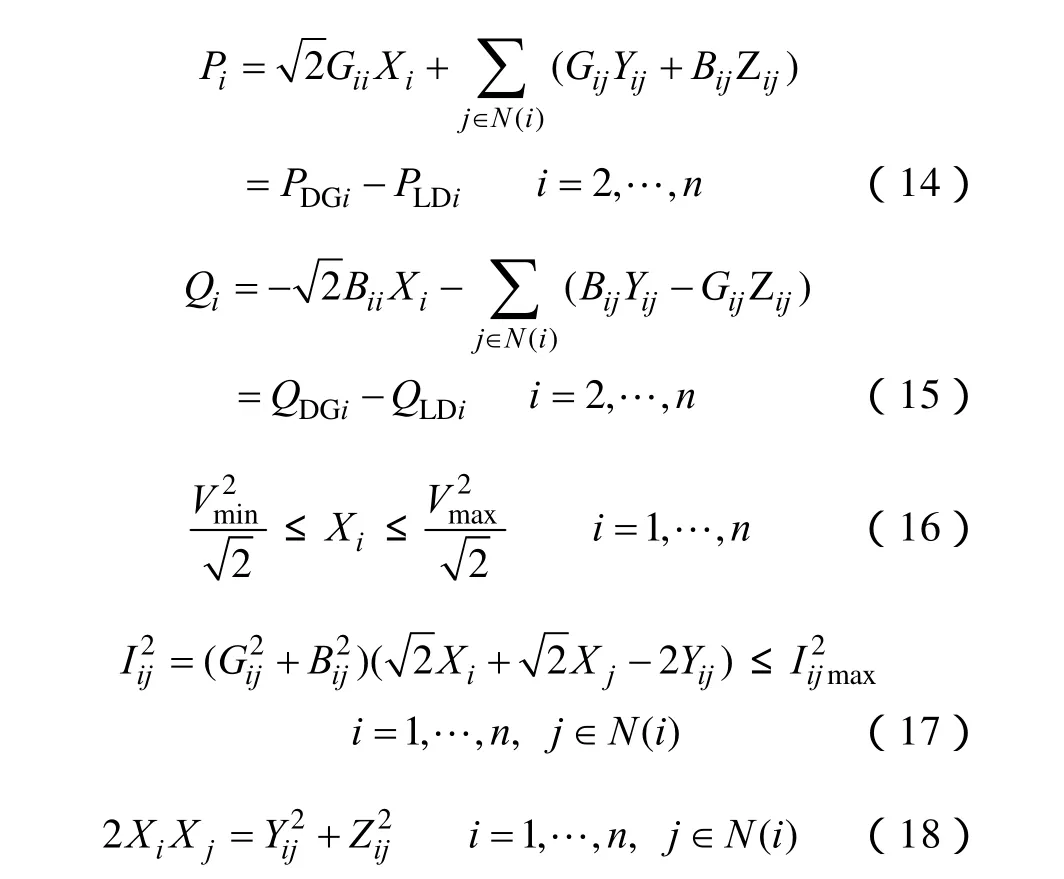
由式（12）可发现，替换后的变量自然满足式（18）的等式约束，式（13）～式（17）所形成的约束条件与原问题的等价。其中，式（13）满足锥优化方法对目标函数的线性要求，式（14）～式（17）满足线性约束条件的要求。式（18）刚好可使得电压决策变量构成旋转锥的笛卡尔乘积形式，满足搜索空间在凸锥的范围内。对此模型，在采用较成熟的求解工具进行求解时，需将式（18）修改为

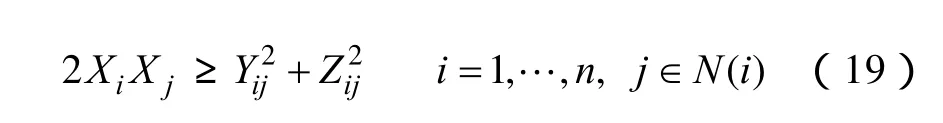
这一处理虽扩大了解的搜索空间，但并不改变解的最优性。这一点可在后续的优化结果中得到验证。

3.2.2 DG约束条件的锥转化

基本约束条件的锥转化方法[16]仅对系统运行约束中的电压变量Vi、Vj和θij的线性变换进行阐述说明，而未涉及分布式电源自身运行约束的转换。因此，本文还需对只含决策变量PDGi、QDGi的分布式电源约束条件进行锥转化。

通过观察可知，式（6）为非线性不等式约束，既不满足锥优化模型对于线性约束的要求，也不满足旋转锥的约束形式。因此，本文提出分布式电源接入容量约束的锥转换公式

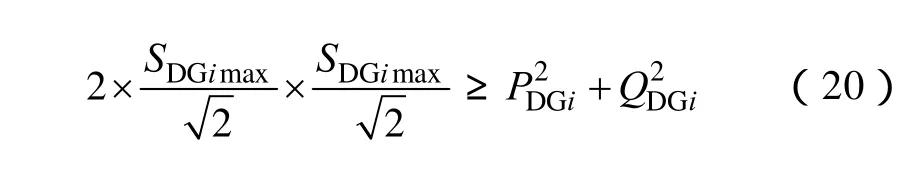
式（20）不仅与式（6）等价，且刚好可使得决策变量PDGi、QDGi构成旋转锥的笛卡尔乘积形式，满足搜索空间在凸锥的范围内。而式（7）～式（9）为线性等式/不等式约束，满足锥优化算法中对线性约束条件的要求，无需进行转化。

因此，式（7）～式（9）及式（12）～式（20）从经济运行的角度出发，综合考虑分布式电源无功输 出 特 性 ， 构 成 了 以 Xi、Xj、 Yij、Zij、PDGi、QDGi为决策变量的分布式电源优化配置的锥优化模型。

4 分析与验证

本文采用Mosek数学工具在IEEE 33节点算例上对上述锥优化模型转换方法的有效性进行测试验证，如下图所示。首先，针对锥优化算法求解潮流的正确性进行验证；然后，对不同 DG接入情况下的锥优化算法的寻优能力及收敛特性进行测试并与 PS、SA算法进行对比。最后，基于网损灵敏度方法[21]进行选址，分析了不同渗透率、不同功率因数下的DG配置方案对配电系统经济运行的优化作用。

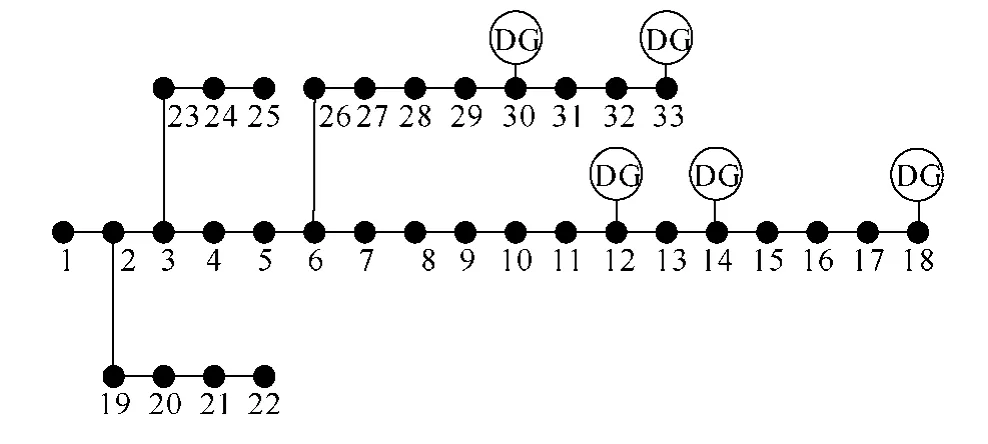
图 IEEE 33配电系统结构图Fig. The structure of IEEE 33 case

4.1 锥优化算法验证

锥优化算法可在优化分布式电源容量的同时对系统的潮流状态进行求解。为验证锥优化算法求解潮流的正确性，采用美国电科院（EPRI）研发的配电网仿真平台OpenDSS作为检验标准，将二者的潮流计算结果进行对比，具体数据详见表1。

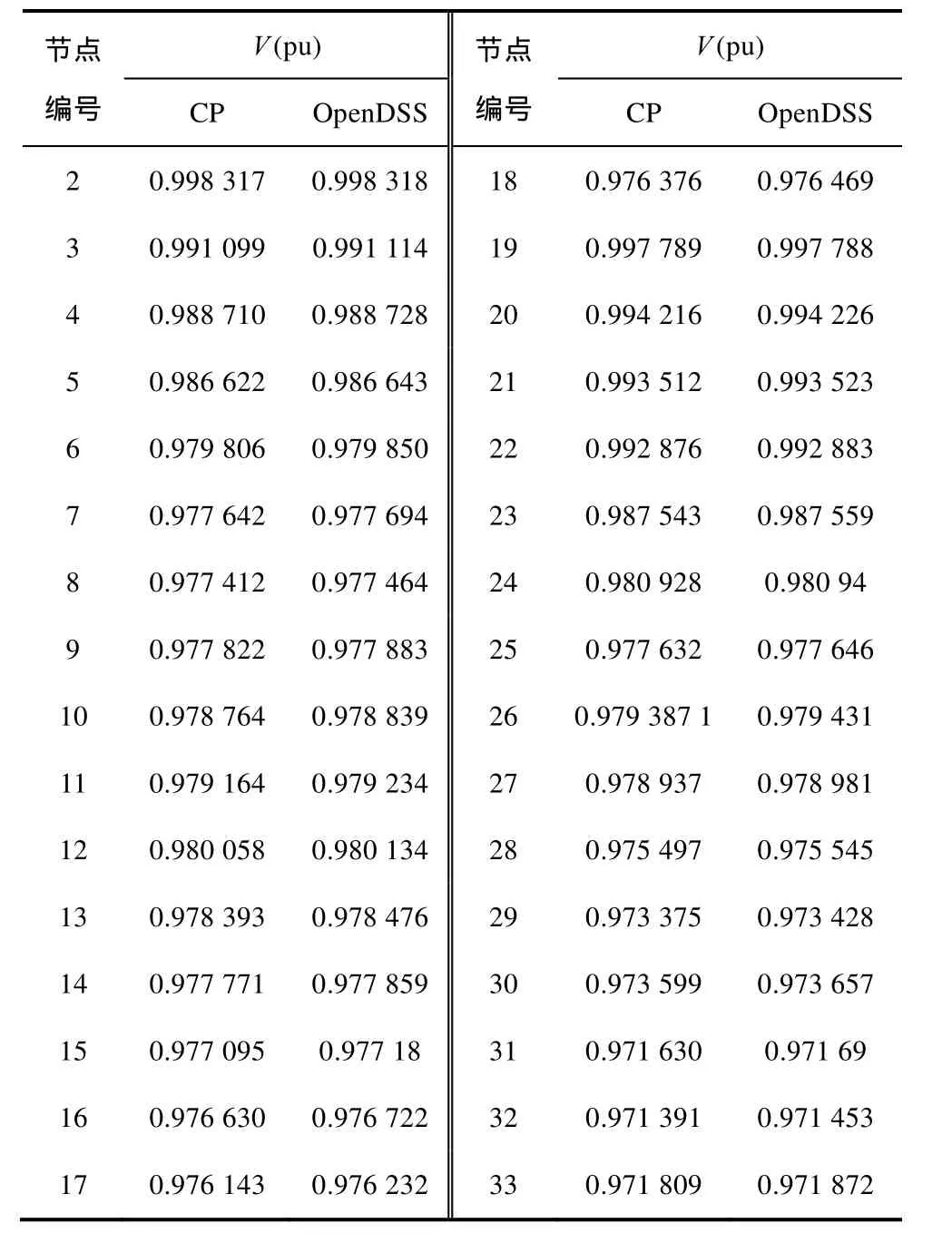
表1 锥优化算法与OpenDSS的潮流结果对比Tab.1 Comparison of power flow results between CP algorithm and OpenDSS

由表1可知，二者的电压计算结果十分相近，最大偏差量为 0.000 93。可见，锥优化算法能够精确地实现潮流求解，而潮流结果的一致性也验证了将式（18）扩大为式（19）并未改变原问题的解。另外，与OpenDSS相比CP算法的电压计算结果略低，这并非二者进行潮流计算的收敛精度不同，而是仿真工具内置的数值计算精度不同，在数据写入读出过程中小数位的取舍所致。所以，在计算需要各节点电压、支路电流不断加和的参量（如网损）时，二者的计算结果则会因为单个小偏差的逐渐累积体现为更大的偏差。

在优化搜索方面，锥优化算法通过对优化模型进行线性化处理，将决策变量的搜索空间限制为凸锥，以大幅度缩减寻优范围来提高优化效率。为进一步验证上述锥转化模型的正确性及锥优化算法的高效性，将 CP与模式搜索法及模拟退火法进行比较（二者均采用OpenDSS计算潮流），随机选取分布式电源的接入位置，针对不同的DG个数及渗透率水平分别对3种算法进行100次测试，统计结果详见表2。

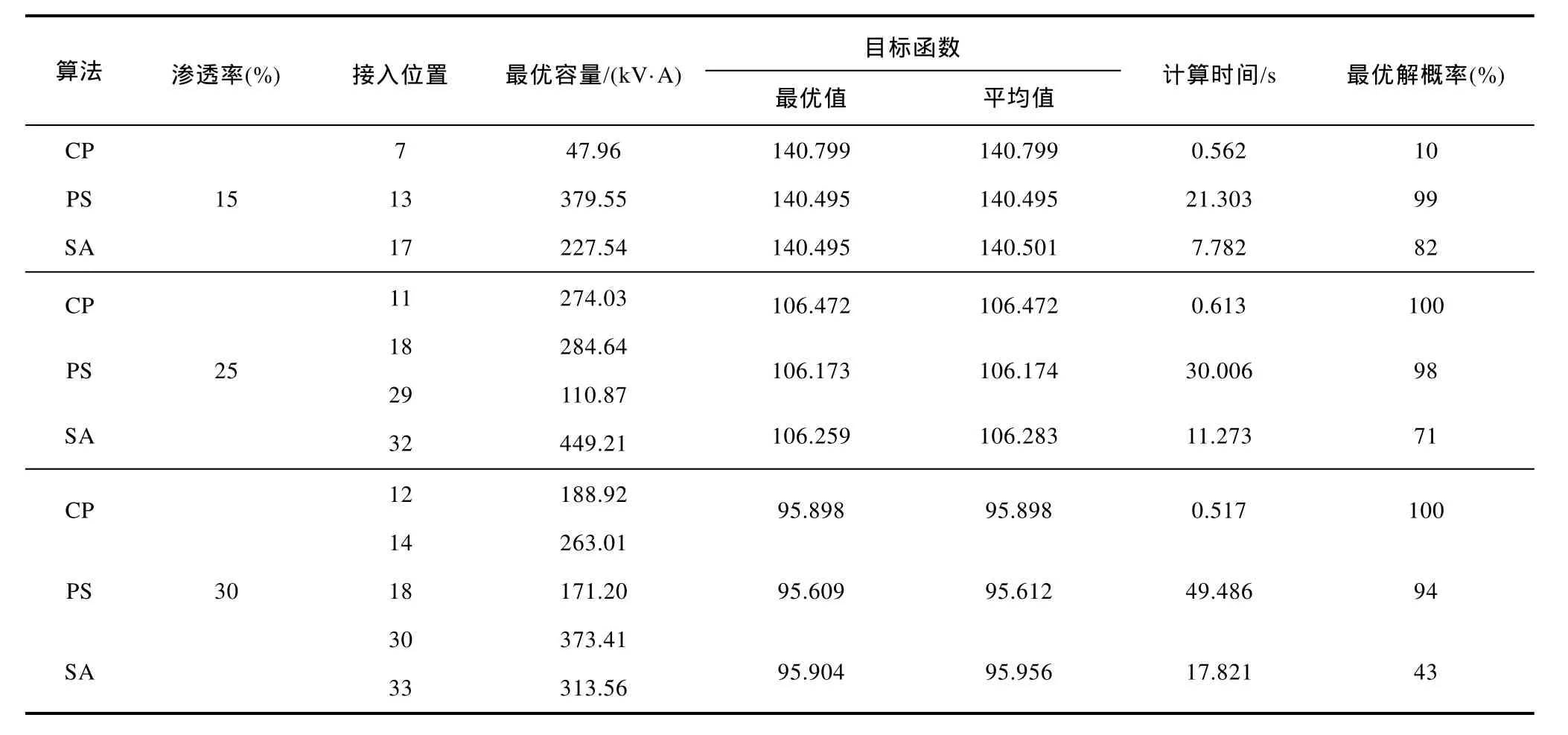
表2 锥优化算法收敛特性测试结果Tab.2 Comparison of convergence for the CP, PS and SA algorithm

表2所示测试结果表明，与模式搜索法及模拟退火法相比，锥优化算法大幅度提高了搜索过程的求解速度，并且在解的最优性上具有很强的稳定性。

首先，最优解概率统计结果显示不同DG接入情况下，CP算法的全局寻优概率均为100%，PS、SA算法的寻优能力则随决策变量的增多而有所降低，且 SA的不确定性尤为显著，然而，二者目标函数的最优值和平均值相差甚小，可见此两种算法虽然不能保证解的最优性，但其优化所得的次优解足以接近最优解。由此可知，锥优化算法通过对原优化问题的锥转化，避免了SA、PS算法陷入局部极值的情况，能够保证解的全局最优性。其次，计算时间统计结果显示，CP算法的运行时间均在 1s以内，计算时间不随决策变量的增多而急剧增长，而 PS、SA算法的计算时间则随优化维数的升高而增长，其中 PS算法运行时间的增长更为突出。可见，对于大规模系统进行优化求解时，PS、SA的计算量问题将使其可实现性受到制约，与之相反，PC计算速度的高效性将更加明显。最后，PS、SA算法的最优性、求解效率和收敛特性往往取决于初始可行解、控制量的选择，应用前需根据大量测试经验来设置相应参数，即一旦问题规模有所改变控制量就需重新选取，而CP算法则无此问题。因此，锥优化算法在计算速度、收敛特性及全局最优性上显出极大优势。需要注意，PS和SA的最优目标函数值虽小于锥优化方法，但这并非 CP算法未搜索到最优方案，而是由数学仿真工具内置数值计算精度所致，三者的最优结果实则是一致的。

综上所述，将锥优化算法应用于分布式电源优化配置问题中，不仅能实现问题的快速、有效求解，还能保证所求解的最优性。

4.2 优化结果分析

根据目标函数值信息采用网损灵敏度分析法[21]进行选址，选取12、14、18、30、33为DG的接入节点，将不同DG接入渗透率水平、不同功率因数下的目标函数值进行对比，结果见表3。

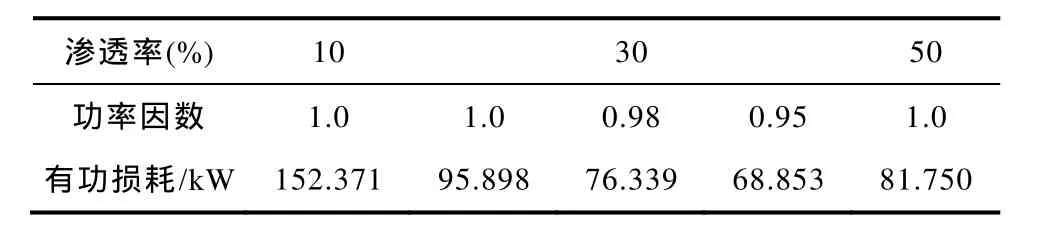
表3 不同渗透率、不同功率因数下的系统有功损耗Tab.3 Comparison of loss under different scenarios

由表3所示的有功损耗对比结果可见，在保证系统安全可靠运行的前提下，分布式电源的降损作用随渗透率的增大而愈加显著。并且，相对于增加有功渗透率接入水平，通过调节分布式电源的无功出力对系统的降损效果更为显著。因此，在DG优化定容问题上，应综合考虑分布式电源的无功输出特性，将无功出力同样作为优化对象，在促进系统经济高效运行的同时进一步发挥了 DG的潜在效益。另一方面，上述优化结果也一并验证了通过锥优化方法所转化的DG优化定容模型的合理性和有效性。

5 结论

随着电力产业日臻朝着环境友好、可持续发展的方向迈进，加速绿色分布式能源的大规模并网应用将成为发展趋势。分布式电源数量的急剧增加使其优化规划问题的维数迅速扩大，因而计算量随之呈现爆炸式增长。因此，快速、准确、高效的优化算法将是分布式电源优化配置的研究重点之一。为此，本文应用锥优化方法对分布式电源优化配置问题进行求解。与传统的智能化算法相比，锥优化方法通过对模型的转化和统一求解，既可实现多个分布式电源的同时优化，又可避免大量的迭代计算和繁琐的测试，极大地提高了计算效率，并能保证解的全局最优性。由于其兼并快速收敛和最优求解的特性，锥优化方法也将为大规模配电网的综合规划优化、运行管理优化以及经济环保效益优化等问题的求解提供一个强有力的支持工具。

[1] 王成山, 李鹏. 分布式发电、微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2): 10-14.Wang Chengshan, Li Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[2] 邓威, 李欣然, 李培强. 基于互补的间歇性分布式电源在配电网中的优化配置[J]. 电工技术学报,2013, 28(6): 216-225.Deng Wei, Li Xinran, Li Peiqiang. Optimization allocation of distributed generations embedded in distribution network[J]. Power System Protection and Control, 2013, 28(6): 216-225.

[3] Abdi Sh, Afshar K. Application of IPSO-Monte Carlo for optimal distributed generation allocation and sizing[J]. International Journal of Electrical Power & Energy Systems, 2013, 44(1): 786-797.

[4] 邓威, 李欣然, 刘志勇, 等. 考虑无功补偿影响因素 的间歇性分布式电源综合优化配置[J]. 中国电机工程学报, 2012, 32(10): 80-88.Deng Wei, Li Xinran, Liu Zhiyong, et al. Comprehensive optimal allocation of intermittent distributed generation considering reactive power compensation[J].Proceedings of the CSEE, 2012, 32(10): 80-88.

[5] 裴玮, 盛鹍, 孔力, 等. 分布式电源对配网供电电压质量的影响与改善[J]. 中国电机工程学报, 2008,28(13): 152-157.Pei Wei, Sheng Kun, Kong Li, et al. Impact and improvement of distributed generation on distribution network voltage quality[J]. Proceedings of the CSEE,2008, 28(13): 152-157.

[6] AlAbri R S, El-Saadany E F, Atwa Y M. Optimal placement and sizing method to improve the voltage stability margin in a distribution system using distributed generation[J]．IEEE Transactions on Power Systems, 2013, 28(1): 326-334.

[7] Hien N C, Mithulananthan N, Bansal R C. Location and sizing of distributed generation units for loadabilty enhancement in primary feeder[J]. Electrical Power Energy and Systems, 2013, 7(4): 797-806.

[8] Shaaban M F, Atwa Y M, El-Saadany E F. DG allocation for benefit maximization in distribution networks[J]. IEEE Transactions on Power Systems,2013, 28(2): 639-649.

[9] Acharya N, Mahat P, Mithulananthan N. An analytical approach for DG allocation in primary distribution network[J]. Electrical Power Energy and Systems,2006, 28(10): 669-678.

[10] AlHajri M. Sizing and placement of distributed generation in electrical distribution systems using conventional and heuristic optimization methods[D].Halifax, Nova Scotia: Dalhousie University, 2009.

[11] 麻秀范, 崔换君. 改进遗传算法在含分布式电源的配电网规划中的应用[J]. 电工技术学报, 2011,26(3): 175-181.Ma Xiufan, Cui Huanjun. An improved genetic algorithm for distribution network planningwith distributed generation[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 175-181.

[12] 于青, 刘刚, 刘自发, 等. 基于量子微分进化算法的分布式电源多目标优化规划[J]. 电力系统保护与控制, 2013, 41(14): 66-72.Yu Qing, Liu Gang, Liu Zifa, et al. Multi-objective optimal planning of distributed generation based on quantum differential evolution algorithm[J]. Power System Protection and Control, 2013, 41(14): 66-72.[13] Pandi V R, Zeineldin H H, Xiao W. Determining optimal location and size of distributed generation resources considering harmonic and protection coordina-tion limits[J]. IEEE Transactions on Power Systems,2013, 28(2): 1245-1254.

[14] Afzalan M, Taghikhani M A, Sedighizadeh M. Optimal DG placement and sizing with PSO & HBMO algorithms in radial distribution networks[C]. 2012 Proceedings of 17th Electrical Power Distribution Networks Conference, 2012: 1-6.

[15] Andersen E D, Roos C, Terlaky T. On implement a primal-dual interior point methods for conic quadratic optimization[J]. Mathematical Programming, 2003,95(2): 249-277.

[16] Jabr R A, Singh R, Bikash C P. Minimum loss network reconfiguration using mixed-integer convex programming[J]. IEEE Transaction on Power Systems,2012, 27(2): 1106-1115.

[17] Jabr R A. Radial distribution load flow using conic programming[J]. IEEE Transactions on Power Systems,2006, 21(3): 1458-1459.

[18] 朱勇, 杨京燕, 张冬清. 基于有功网损最优的分布式电源规划[J]. 电力系统保护与控制, 2011, 39(21):12-16.Zhu Yong, Yang Jingyan, Zhang Dongqing. Planning of distributed generation based on optimal real power losses[J]. Power System Protection and Control, 2011,39(21): 12-16.

[19] Elnashar M M, El-Shatshat R, Salama M A. Optimum siting and sizing of a large distributed generator in a mesh connected system[J]. Electrical Power Energy and Systems, 2010, 80(6): 690-697.

[20] 任洪伟, 韩丛英, 裴玮, 等. 基于多目标优化模型的分布式电源选址方案研究[J]. 电力系统保护与控制, 2013, 41(24): 64-69.Ren Hongwei, Han Congying, Pei Wei, et al. Research on distributed generation locating based on multiobjective optimization model[J]. Power System Protection and Control, 2013, 41(24): 64-69.

[21] Khatod D K, Pant V, Sharma J. Evolutionary programming based optimal placement of renewable distributed generators[J]. IEEE Transactions on Power Systems,2013, 28(2): 683-695.