一种有效的被动传感器固定辐射源定位技术*
2014-11-09俞建国邓志安
俞建国, 姚 璐, 黄 强, 邓志安
(1南京电子技术研究所 南京 210039 2江苏省新闻出版学校 南京 210012 3大连海事大学 大连 116026)
引 言
在大多声纳和电子支援ESM(Electronic Support Measure)系统中,利用被动测量角度对辐射源进行定位应用非常普遍。辐射源的位置可以通过空间不同排列的平台测量信息估计出来,平台之间可利用冗余信息互补更好地完成任务。许多成熟方法[1~3]已应用于多平台的辐射源定位场景中,但它们大多没有考虑时空对准的问题,而这在实际应用中是一个复杂的过程。大多情况下,某个时刻不同平台之间的距离要远大于同一个平台相邻时刻的距离,那些成熟的批处理算法,如总体最小二乘算法[4]和奇异值分解算法[5],在单平台的辐射源定位场景中性能往往不尽如人意。近年来,许多学者转向研究单平台的辐射源定位,并取得了一系列的研究结果[6~8]。这些技术大致可以分为以下两类。一类是迭代技术,以扩展卡尔曼滤波EKF(Extended Kalman Filter)、无迹卡尔曼滤波UKF(Unscented Kalman Filter)和粒子滤波PF(Particle Filter)等非线性滤波方法为代表[9,10],这类方法需要传感器测量误差的先验信息,并且通常需要较为准确的到达时间 TOA(Time of Arrival)、到达时差 TDOA(Time Difference of Arrival)[6,7,11,12]、相位差PD(Phase Difference)、到达频差 FDOA(Frequency Difference of Arrival)[7,13]测量值中的一种或者多种。另一类是批处理方法,以最小二乘 LS(Least Square)[4]、最大似然估计 MLE(Maximum Likelihood Estimation)[14]为代表,这类方法以较大的计算量为代价获得较高的定位精度。然而,辐射源定位还存在着一些难点需要进一步探讨。首先,很多情况下传感器测量先验信息并不能真实反映实测数据的误差水平,这会导致结果不可靠,甚至会产生滤波发散;其次,批处理所需的较大计算量对于实时系统的应用是个挑战,并且它不能提供类似误差协方差的指标对定位精度进行评价。鉴于以上原因,在实时系统中利用单平台对辐射源的定位还未得到很好的解决。本文考虑一种更为普遍的定位场景,即单个ESM通过自身的运动,获得轨迹不同时刻测量方位角,进而提取辐射源的位置信息。为此,本文提出了一种基于网格搜索最大后验准则GSMAP(Grid Search Maximum a Posteriori)的辐射源定位算法。该算法利用当前时刻所有的测量角度以及传感器平台的位置,计算综合代价函数,并在上一时刻更新位置周围搜索最合适的位置作为辐射源位置。
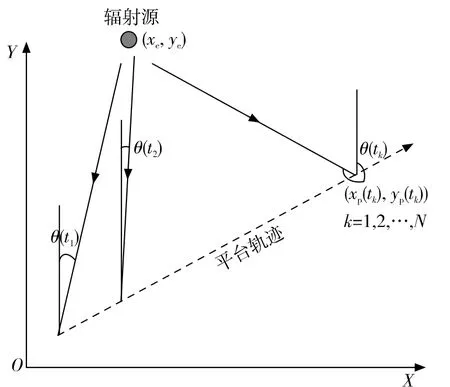
图1 平台轨迹与辐射源的几何关系(北偏东)
1 辐射源定位模型
1.1 辐射源定位描述
假设ESM只能获得带随机误差的方位角,并且研究的范围限制在辐射源和传感器平台处于同一平面内。假设在采样时刻 {tk},k=1,2,…,N,给定平台的位置 xp(tk)、yp(tk)和速度vx(tk)、vy(tk),以及相应的tk时刻从未知位置(xe,ye)的辐射源获得的测量方位角,通过上述信息我们最终要对辐射源位置进行估计。图1所示为平台轨迹与辐射源的几何关系,这里我们采用北偏东参考方向,其它参考方向可进行相应的转换,在此不多阐述。由此,tk时刻获得的方位角可表述为
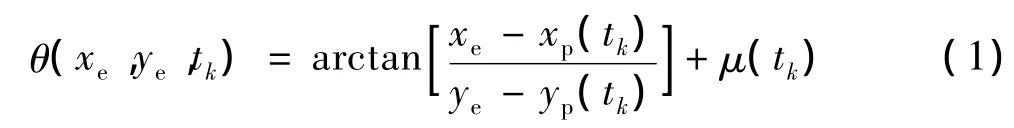
式(1)中,μ(tk)代表tk时刻测量噪声,通常被认为具有已知的先验信息。然而,实测数据往往与先验的统计信息不相符。本文中我们将θ(xe,ye,tk)简写为θ(tk)。从式(1)很明显可看出,θ(tk)的精度取决于测量噪声以及平台轨迹与辐射源之间的几何关系。可观测性反映定位精度与平台轨迹和辐射源几何形状之间的关系,Fisher信息阵和Cramer-Rao界则是评价可观测性的有效准则,但在本文中我们侧重研究的是在某一特定场景下的定位技术。
1.2 实际测量误差
正如前面所述,实测数据中的测量误差往往与先验统计信息不相符。针对该问题,许多学者做了大量的研究,预期获得实测数据的误差分布和水平。然而测量误差与天气、环境、操作员等均密切相关,即使在完全相同的条件下,不同时间获得的测量误差统计结果差异巨大,鲜有公开发表有效的研究结果。图2给出两个不同场景的实测数据的测量误差。
从图2可知,难以采用单一的模型去准确地描述真实测量误差。此外,不同场景的测量误差几乎完全不同,即使在同一个场景,不同时间段的测量误差水平也随着时间在不断变化。因此,对于大多数实测数据,先验的测量误差统计信息往往是不准确的。
2 辐射源定位算法
正如引言所述,本文着重研究单个ESM通过自身的运动,获得轨迹不同时刻测量方位角,进而提取辐射源的位置信息。由于不同时刻ESM获得的角度相差很小,传统的LS方法系数矩阵的条件数过大,导致非线性估计失效。而MLE则需要准确的传感器测量误差先验统计信息,否则似然函数建立不准确。因此本文将研究不依赖于传感器测量先验信息的批处理定位算法。
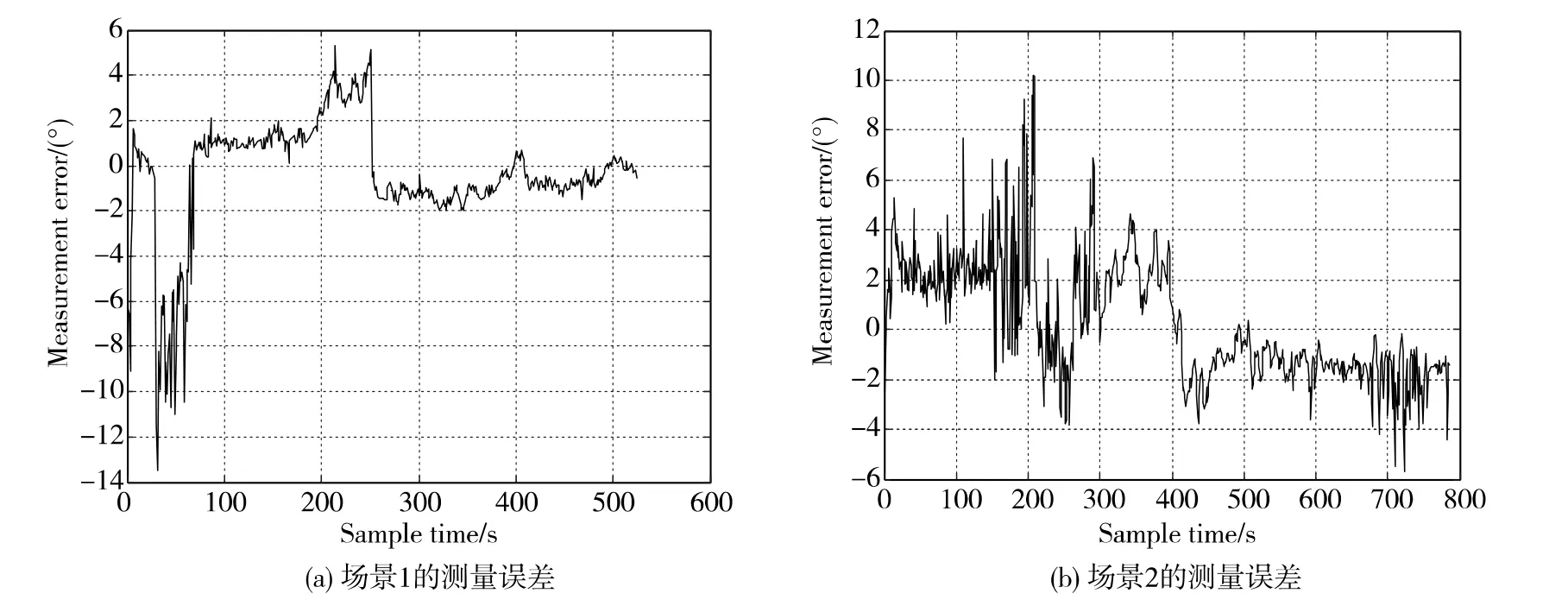
图2 实测数据的测量误差
2.1 网格搜索最大后验准则算法
本文所提出的GSMAP批处理方法的中心思想描述如下:在关注的监视区域中,通过平台和所估计辐射源的位置计算一组后验方位角,同时搜索辐射源位置,使得该位置获得的后验方位角最接近测量方位角。图3为GSMAP的示意图。对于每个采样时刻tk,仅有一个测量值θ(tk),但有M2个后验方位角,表述为η(tk,l),l=1,2,…,M2,M为网格搜索深度,L为网格搜索步进。^X(tk-1)为tk-1时刻辐射源的估计位置,而˜X(tk,l)为tk时刻辐射源的第l个候选位置。
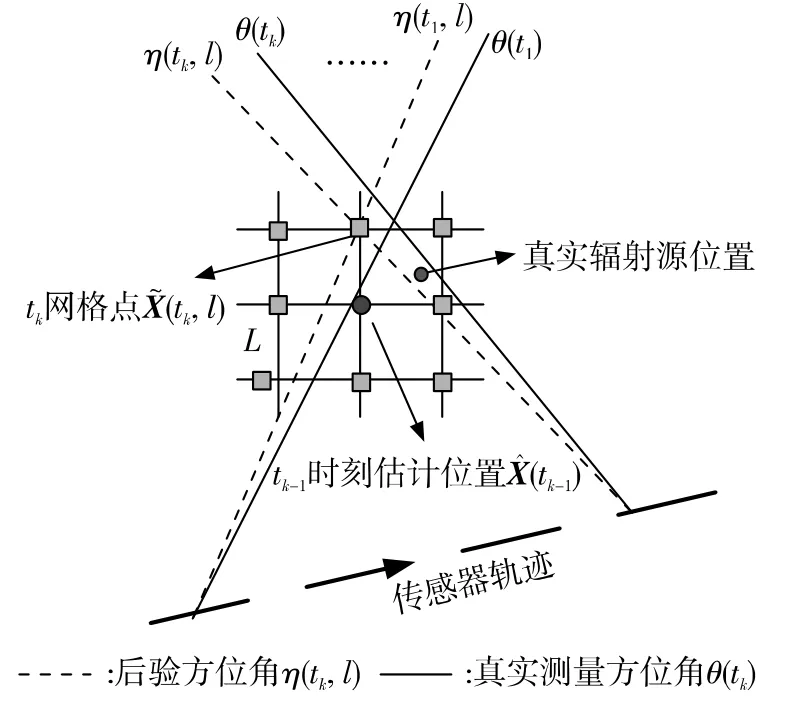
图3 GSMAP示意图
2.2 GSMAP算法描述
下面我们给出tk时刻的GSMAP简要过程描述。
①获取初始定位。通过对初始的一些方位角进行交叉定位获得初始状态,表示为Xinitial=[x0,y0]T。
②划分网格点。在 ^X(tk-1)附近划分M2个网格点(包括它本身),这样就可以得到tk时刻辐射源M2个候选位置,表示为{(tk,l)},l=1,2,…,M2。
③计算后验方位角。利用tk时刻平台的位置以及辐射源候选点位置,可以得到tk时刻全部候选点的后验方位角
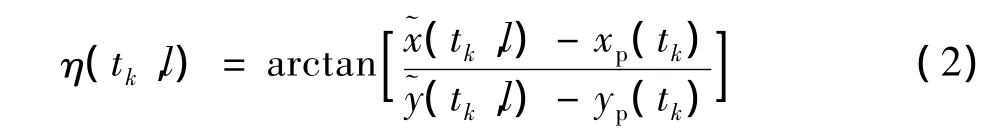
这里,l=1,2,…,M2,k=1,2…,N,N 表示测量数据个数。
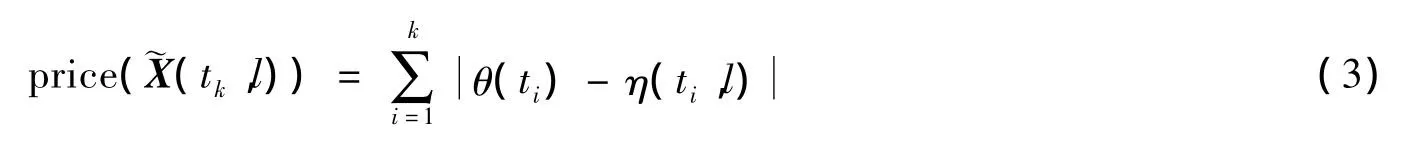
⑤最优搜索。我们从这M个候选网格点中寻找代价函数最小的候选点,作为tk时刻辐射源的最优位置,表达式如下
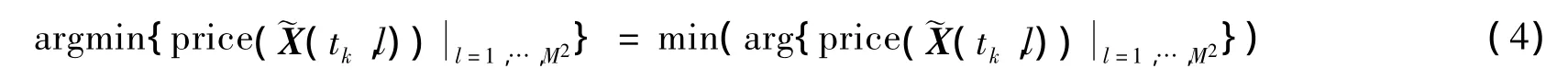
满足式(4)的候选点将作为tk时刻最优的辐射源位置赋值给(tk)。
3 结果与分析
本节中,为验证本文所提出的GSMAP定位算法的性能,设计了相应的仿真场景,并在同等条件下比较了EKF和UKF等典型非线性滤波方法的跟踪效果,从而验证了本文所提出的GSMAP算法的优越性。仿真中GSMAP算法的搜索步长为200m,搜索深度为5。
3.1 测量误差已知的仿真结果
在测量误差服从高斯分布且标准差已知的前提下,比较传统EKF、UKF和GSMAP的性能。
目标位于原点中心,载机起始位置为[-50km,-89km],沿着正北方向以200m/s的速度运动,持续时间300s,采样周期为1s,传感器测角误差为1°。图4为传感器与目标的二维场景图,图5为对应的测量方位角。
共进行50次蒙特卡洛仿真,图6比较了不同算法的定位性能,图7为图6的局部放大图。从图5可知,测量方位角抖动程度比较平稳,且服从标准差为1°的高斯分布。分析图6和图7可知,在该仿真场景中,EKF和UKF的定位均方根误差几乎完全一致,UKF定位精度仅比EKF高出不超过10m。这也从侧面说明了迭代滤波算法只利用最近的测量值对状态进行更新,在较短时间内估计精度提升很有限。而GSMAP在获得初始位置(30个方位角)后,迅速逼近辐射源真实位置,在第100s定位误差大约为5km,而EKF和UKF达到此精度需要230s,最终GSMAP定位误差为560m,而EKF和UKF的定位精度约为2km。
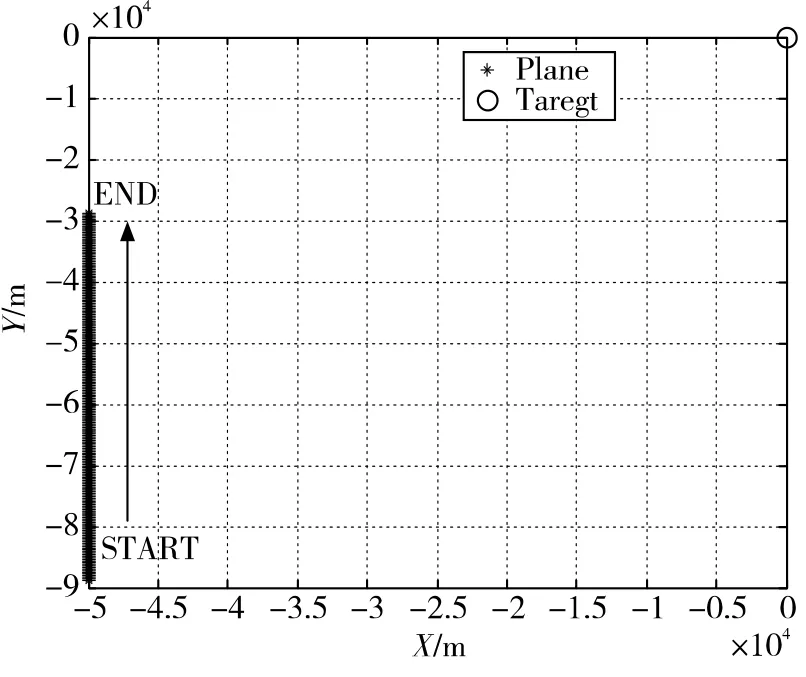
图4 传感器与目标二维场景图
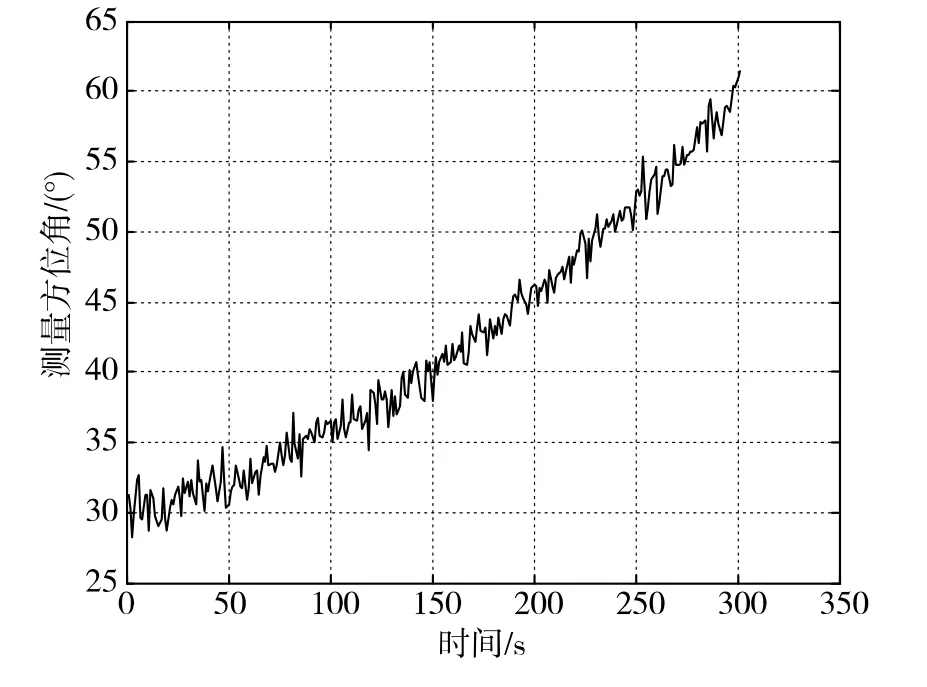
图5 已知测量误差测量方位角
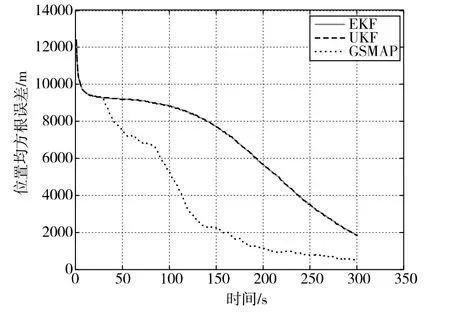
图6 不同算法定位性能比较
当然,GSMAP的高精度定位结果是建立在相对较大的运算量基础上的,该算法第k时刻定位需要计算k·M2个后验角度。但在实际应用场景中,由于受到载机飞行包线以及天线方向性的影响,ESM获得的有效数据往往较短,因此本文所提算法具有较强的实用性。针对大数据量的特定辐射源定位场景,目前正在进一步研究数据稀释以及加窗的方法来提高实时性。
3.2 测量误差未知的仿真结果
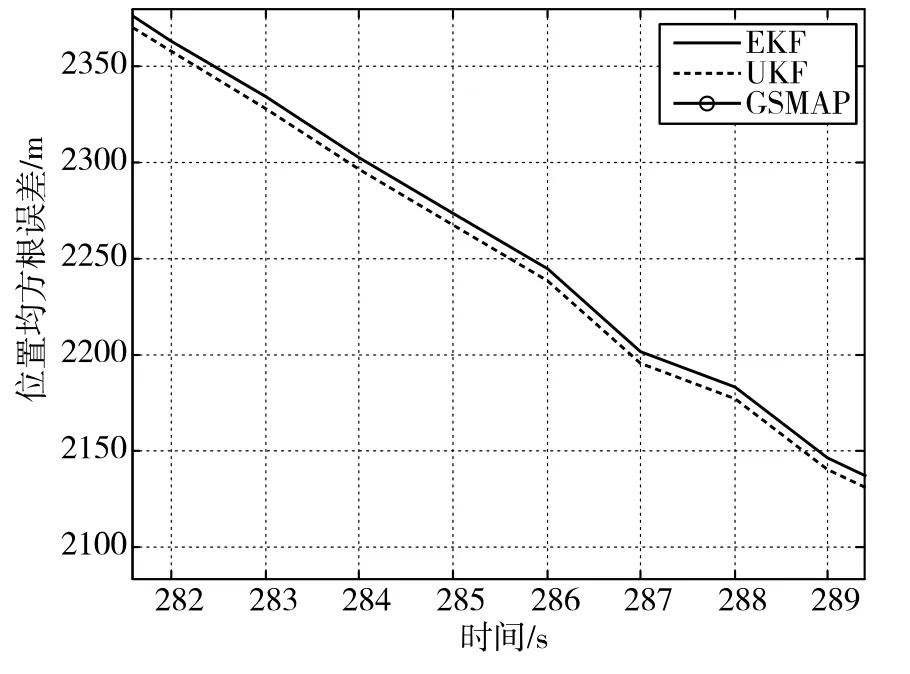
图7 不同算法定位性能比较(局部放大)
正如前面所述,传感器真实的测量误差往往是未知的或者不准确的,本节将验证GSMAP在测量误差未知时的定位性能。仿真场景与3.1节完全一致,传感器测量误差在1°~3°之间随机变化。图8为测量误差未知时的测量方位角,图9为50次蒙特卡洛仿真得到的不同算法的定位性能比较。对比图8和图5,最明显的区别是图8的方位角抖动是时变的,而非平稳过程。从图9可知,当测量误差未知时,EKF和UKF采用的测量误差协方差与真实测量误差失配,导致跟踪性能下降,即定位误差达到5km需要280s,最终定位精度为4km。而GSMAP因为采用批处理的方式,对单次测量误差不敏感,所以定位误差和收敛速度与测量误差已知时相比并没有多大的区别,仅在150s~250s期间角度抖动最为厉害时刻,其定位误差稍有增加,但当角度抖动减弱后,GSMAP定位误差迅速下降。最终GSMAP算法定位误差为712m,远远优于EKF和UKF的3.98km。
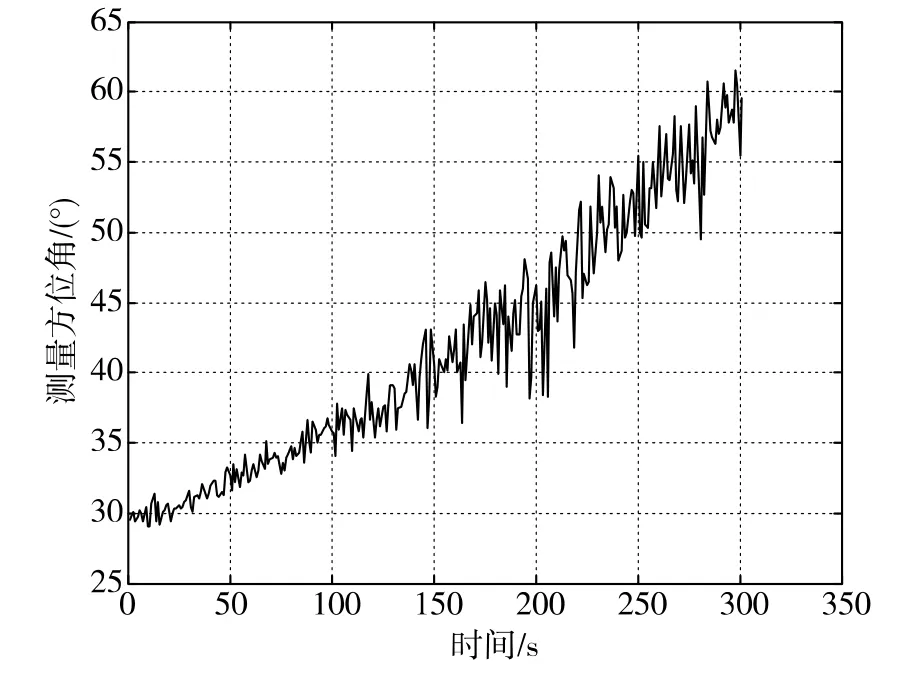
图8 测量误差未知时的测量方位角
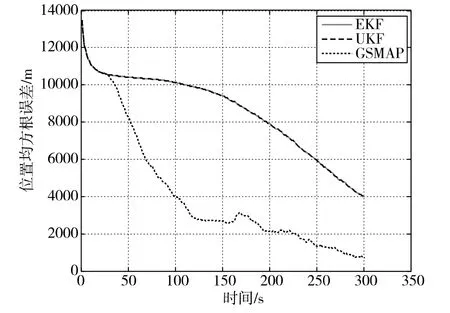
图9 测量误差未知时不同算法定位性能比较
4 结束语
针对传感器测量误差先验信息未知的情况,本文提出了一种有效的被动传感器辐射源定位算法,它采用当前时刻所有测量方位角以及传感器平台位置构造代价函数,通过搜索候选网格点综合代价函数最小的位置确定当前时刻辐射源的最优位置。仿真实验证明,本文所提出的GSMAP算法无论在定位精度还是收敛速度上,远优于传统的非线性估计方法,同时该算法无需准确的测量误差先验信息,具有较强的鲁棒性。本文所提方法能为工程上的辐射源定位提供一种可用、有效的工具。
[1]Kreucher C,Shapo B.Multitarget Detection and Tracking Using Multisensor Passive Acoustic Data[J].IEEE Journal of Oceanic Engineering,2011,36(2):205 ~218.
[2]Adrian N B,Pubudu N P.Localization of Emitters via the Intersection of Bearing Lines:a Ghost Elimination Approach[J].IEEE Transactions on Vehicular Technology,2007,56(5):3106 ~3110.
[3]Zhou Li,Li Lingyun,He You.New Multi-layer Data Correlation Algorithm for Multi-passive-sensor Location System[J].Journal of Systems Engineering and Electronics,2007,18(4):667 ~672.
[4]Hmam H,Dogancay K.Passive Localization of Scanning Emitters[J].IEEE Trans.on Aerospace and Electronic Systems,2010,46(2):944 ~951.
[5]T.Patrik Nordberg,Ivar Gustafsson.Using QR Factorization and SVD to Solve Input Estimation Problems in Structural Dynamics[J].Computer Methods in Applied Mechanics and Engineering,2006,195(44-47):5891 ~5908.
[6]Okello N,Fletcher F,Musicki D,Ristic B.Comparison of Recursive Algorithms for Emitter Localisation Using TDOA Measurements from a Pair of UAVs [J].IEEE Trans.on Aerospace and Electronic Systems,2011,47(3):1723~1732.
[7]Yeredor A,Angel E.Joint TDOA and FDOA Estimation:A Conditional Bound and Its Use for Optimally Weighted Localization [J].IEEE Trans.on Signal Processing,2011,59(4):1612 ~1623.
[8]Becker K.Passive Localization of Frequency-agile Radars from Angle and Frequency Measurements[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(4):1129 ~1144.
[9]Rui Liyang,Xu Zhen.A Fast Global Node Selection Algorithm for Bearings-only Target Localization [J].Chinese Journal of Aeronautics,2008,21(1):61~70.
[10]Zhang Hongjian,Jing Zhongliang,Hu Shiqiang.Localization of Multiple Emitters Based on the Sequential PHD Filter[J].Signal Processing,2010,90(1):34 ~43.
[11]Shen Junyang,Molisch A F,Salmi J.Accurate Passive Location Estimation Using TOA Measurements[J].IEEE Transactions on Wireless Communications,2012,11(6):2182 ~2192.
[12]Liu Congfeng,Yang Jie,Wang Fengshuai.Joint TDOA and AOA Location Algorithm [J].Journal of Systems Engineering and Electronics,2013,24(2):183 ~188.
[13]Musicki D,Kaune R,Koch W.Mobile Emitter Geolocation and Tracking Using TDOA and FDOA Measurements[J].IEEE Trans.on Signal Processing,2010,58(3):1863 ~1874.
[14]Doganay K.Online Optimization of Receiver Trajectories for Scan-based Emitter Localization [J].IEEE Trans.on Aerospace and Electronic Systems,2007,43(3):1117 ~1125.
