无人机自组网分布式时间同步方案研究

侯延顺， 孙甲琦， 王晓波， 龚少华

(1北京遥测技术研究所 北京 100076 2酒泉卫星发射中心 北京 100162)

引 言

网络时间同步是无人机自组网中的一项关键技术，是完成多址接入、功率控制、同步跳频、数据聚合等功能的核心技术和前提。目前，自组网中采用的同步技术主要有以下几种[1～6]:①各节点分别采用高精度的时钟;②利用GPS时标作为时间基准;③采用临时群首作为时间主控节点来实现网络的同步;④自组织网络的分布式同步技术。方式①在具体实现时成本很高;方式②依赖于GPS时标信号;方式③依赖主控节点，且远端节点的同步精度受累积误差的影响较大;方式④分布式同步技术凭借组网速度快、抗毁性强、适于节点的快速移动等特点成为国内外研究的热点[1～3，7～11]。本文提出一种分布式时间同步方案，并针对该方案应用于无人机自组网中的关键问题提出了解决方法。

1 分布式时间同步方案介绍

分布式时间同步方案分为双向时间信息交互和本地时间调整两部分。

1.1 双向时间信息交互

每隔一个同步周期，网络中各节点均与其所有的邻居节点进行双向时间信息交互，以计算其和邻居节点的时间偏差。同步周期的长短根据晶振的稳定度和同步精度要求来确定。

图1展示了一对相邻节点a和b之间进行双向时间信息交互的工作过程。在ta时刻，节点a发送时间交互分组，并把发送时刻ta写在分组内;节点b在tba时刻收到来自节点a的分组，并在tb时刻进行回复，同时把tba和tb写在分组内;回复的报文在tab时刻到达节点a。这四个时间存在着如下关系:

其中，td为单向传播时延(假定节点静止)，tΔ为两个时钟之间的相对偏差。

根据式(1)，可以求出传播时延和时钟偏差:

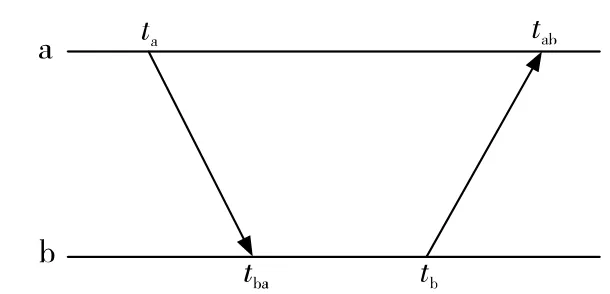
图1 双向时间信息交互过程

需要注意的是，节点b是无法直接获得tab的，但可以按照节点相对距离不变、往返时延相同的情况进行估算。

1.2 本地时间调整

完成双向时间信息交互以后，各节点获得了其与所有邻居节点的时间偏差，进而用加权平均算法计算出一个时间调整量，用来调整本地时间。

本地时间调整算法示意图如图2所示。在第n个时间调整周期，节点5通过双向时间信息交互获得了自身和其邻居节点的时间偏差Δt53(n)、Δt56(n)和Δt59(n)，节点5用这些时间偏差计算出自己的时间调整量

其中，w53、w56、w59是节点5对各邻居节点随机生成的加权系数，满足w53+w56+w59=1。

节点5对本地时间进行调整:

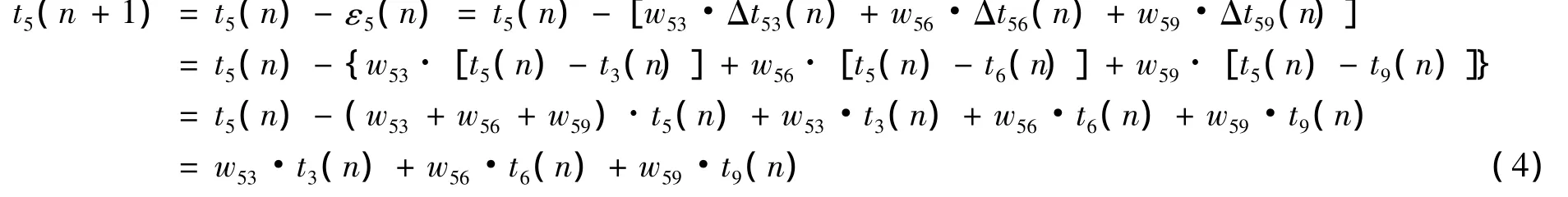
其他节点也做类似的处理。这样，经过若干次的迭代运算，全网时间趋于一致。

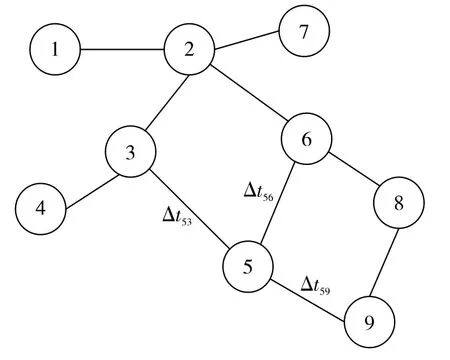
图2 本地时间调整算法示意图

2 分布式时间同步方案中的关键问题

2.1 收敛性问题

由于方案是分布式进行的，没有中心节点的控制，全网时间的同步需要借助具有良好收敛性的时间调整算法来实现，当网络为多跳网络时，这个问题尤为复杂。文献[7]通过图论的方法证明了加权平均算法在静止全连通网络中的收敛性，下面进一步证明该算法在动态、多跳、全连通网络中的收敛性。

符号含义如下:N表示网络中节点个数;ni表示各节点，i∈{1，2，…，N};ti(n)表示第i个节点在第n个同步周期的时间;Ai表示第i个节点的一跳邻居节点构成的集合;Aij表示Ai中同时与节点i和节点j互为邻居节点的集合，其中j为i的邻居节点;wij表示节点i在计算时间调整量时对相邻节点j的加权。

对于一次时间调整:

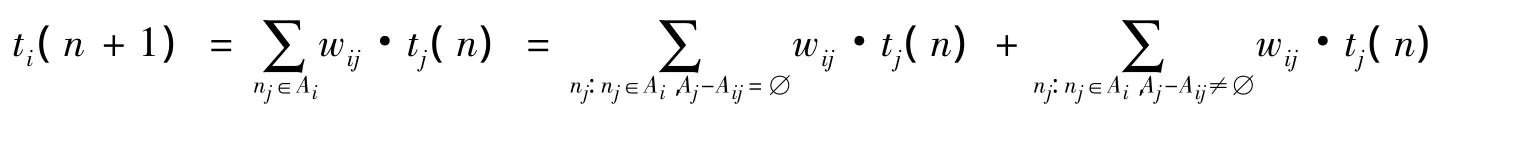
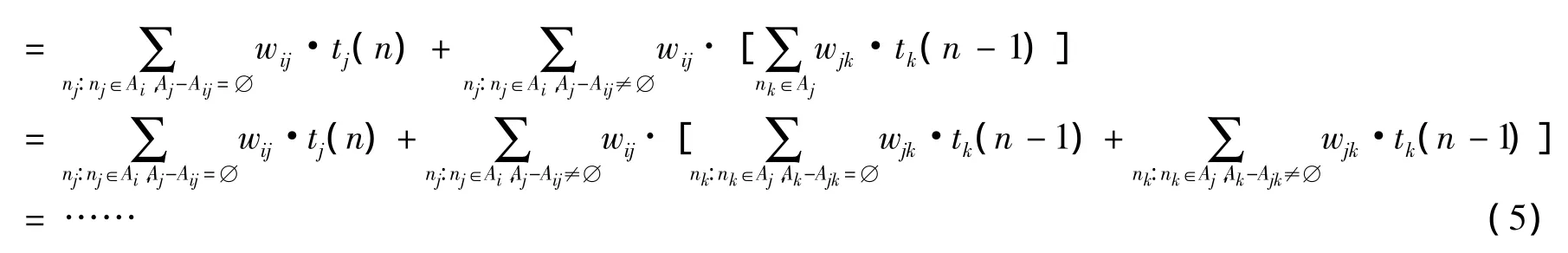
式(5)不断展开，直到遍历网络中的所有节点，此时

令 a(n)=min{ti(n)，i∈{1，2，…，N}}，b(n)=max{ti(n)，i∈{1，2，…，N}}，显然a(n)≤b(n)，经过加权平均后，得到

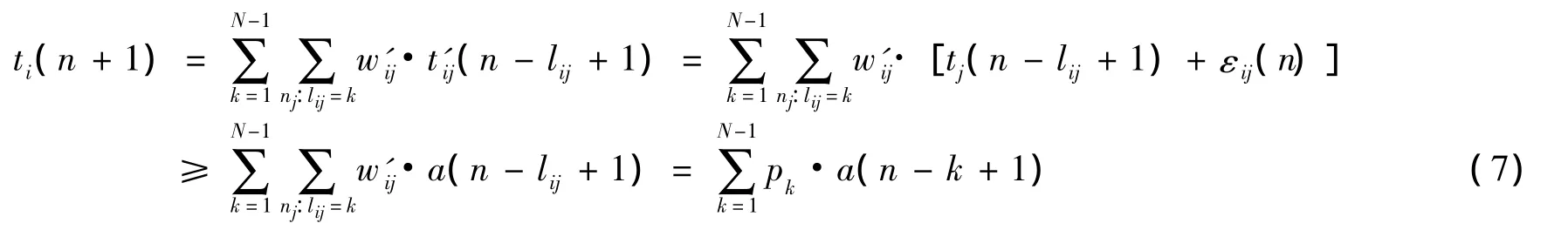
其中，pk是最小跳数为k的各个w'ij组合后得到的系数，。为了保证该式成立，必须限定εij(n)的范围，关于该范围的讨论将在下文进行。

式(7)对所有i成立，包括ti(n+1)的最小值a(n+1)，因此

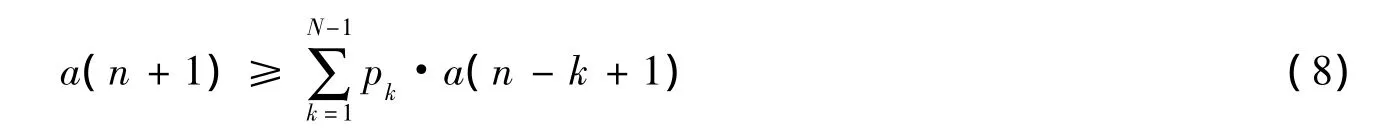
很明显，只有当数列a(n)为一递增数列时，式(8)才能对所有的系数pk成立。这说明，随着迭代次数的增加，所有节点时间的最小值在逐渐增大。

同理，可以证明，随着迭代次数的增加，节点时间的最大值在逐渐减小。

由于a(n)和b(n)都是有界序列，故当n→∞时，a(n)和b(n)都趋于它们的极限。下面证明这两个数列的极限是一致的。

设在n+1时刻，全网时间最小的节点为r，在n-lrq+1时刻，全网时间最大的节点为q，则有

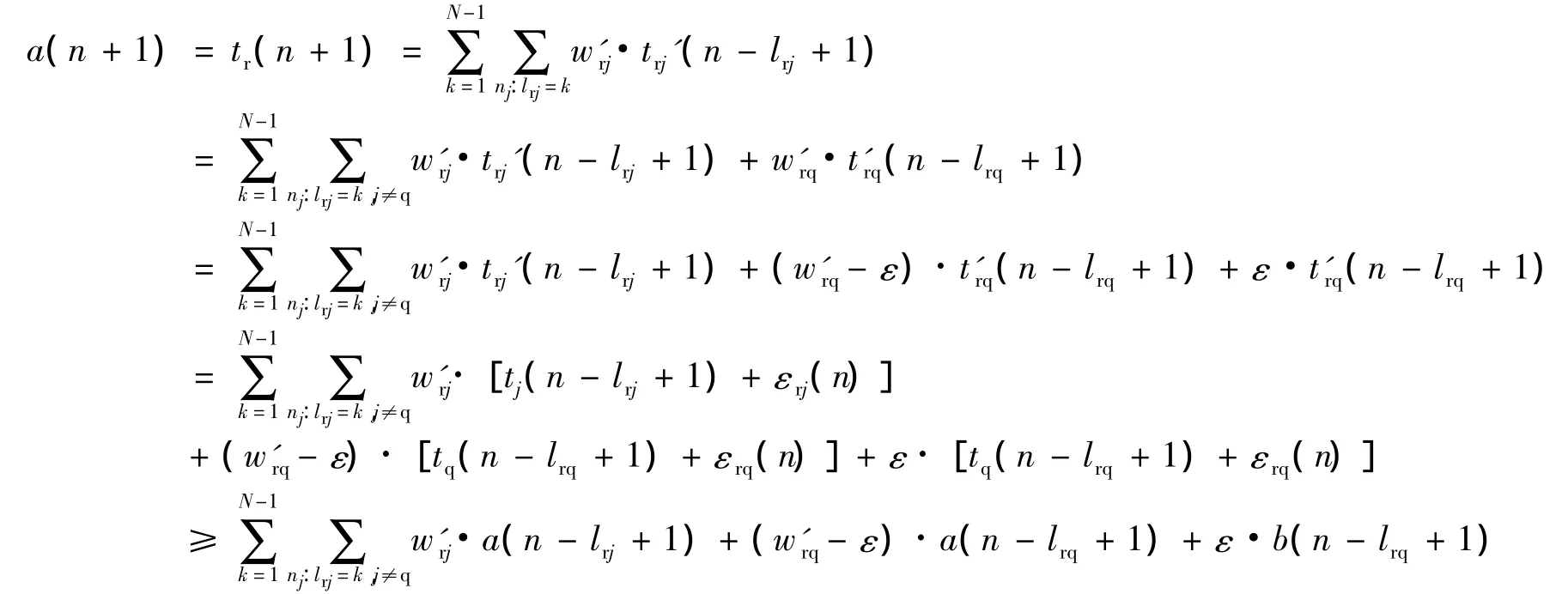
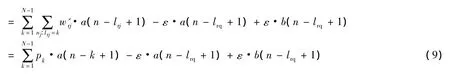
同理，设在n+1时刻，全网时间最大的节点为s，在n-lsp+1时刻，全网时间最小的节点为p，经过类似的推导，可以得到:

将式(9)、式(10)相减，得到:

很明显，只有当数列b(n)-a(n)为一递减数列时，式(11)才对所有pk成立。因此，当n→∞时，b(n)-a(n)趋于0，即a(n)和b(n)趋于同一极限，全网节点能够趋于一致。

2.2 节点移动的影响

在上述收敛性证明里面，我们引入了一个偏差εij(n)，该偏差主要是由节点移动导致的往返时延不一致引起的，只有将其限定在一定范围内，才能保证该方案在无人机自组网这种动态、多跳网络中的收敛性。节点的高速移动除了造成往返时延不一致以外，还会改变拓扑结构，必须对其进行评估和消除[11]。

2.2.1 往返时延不一致

双向时间信息交互主要目的是在测量节点间时钟相对偏差的同时，测量并消除传播时延，其测量方法如图1和式(1)、式(2)所示。然而，上述测量传播时延和时钟偏差的方法是在节点相对距离不变、往返时延相同的前提下得到的，当节点移动导致相对距离变化时，用该方法测得的传播时延和时钟偏差将存在误差。也就是说，由于节点的移动，节点a在ta时刻的位置和节点b在tba时刻的位置之间的相对距离，与节点b在tb时刻的位置和节点a在tab时刻的位置之间的相对距离可能不同，即往返时延td0≠td1，图1中的时间关系应修正为

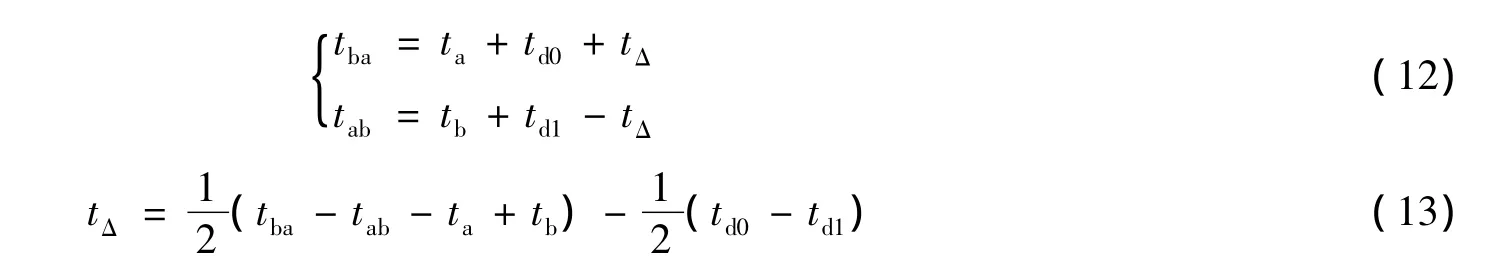
此时，若按照td0=td1的方式计算时钟偏差，就造成了误差。为了保证收敛性和同步精度，必须将该误差限定在一定范围内。

由于节点移动速度与无线电波速度相差甚远，在分组空中传播过程中节点的移动可以忽略不计，因此往返时延的不一致主要取决于一个节点从收到邻居发送的时间交互分组到其回复的时间，记此时间长度为tpw。下面研究在给定的节点移动速度和同步精度要求下tpw的上限。在相同的时间内，两个节点的运动方向相反时，距离变化最大，因此在下面的讨论中，假设一对节点在进行时间信息交互的过程中，始终保持运动方向相反。

如图3，两个节点运动方向相反，节点A在某个时刻发送时间交互分组，节点B收到以后，经过tpw后回复。设节点运动速度为v，则在tpw内由节点移动导致的往返时延之差为

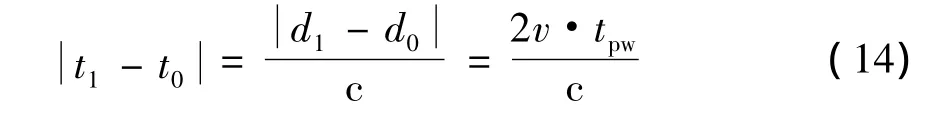
式中，c为光速。时钟偏差的计算误差为

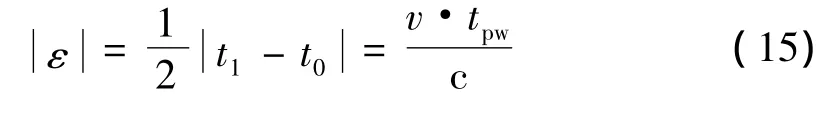
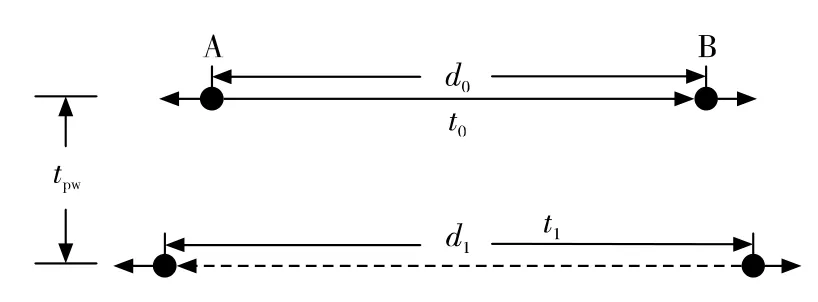
图3 tpw内节点的运动

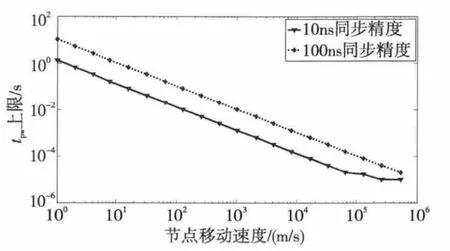
图4 tpw与节点移动速度的关系

据此，通过仿真得到了同步精度分别为100ns和10ns时，在保证完成时钟同步的条件下，tpw与节点移动速度的关系，如图4所示。图4中，横坐标代表节点的移动速度;纵坐标代表在相应的移动速度下，为了保证100ns和10ns的同步精度，tpw所能取的最大值;两个坐标均取对数。

在这里，假设有10个节点，各节点保存一个时钟向量，用以记录各节点的时钟;同时假设其他时延已得到合理消除，把节点移动导致的时钟相对偏差的计算误差计入节点

保存的时钟向量，使用加权平均法进行迭代运算;若在一定的迭代运算后，各节点时钟偏差小于同步精度要求，认为能够完成同步，此时倍增tpw，直到无法完成同步。

表1列出了图4中的一些典型值。

从表1中可以看到:①节点移动速度越快，tpw所允许的上限值越小，两者呈反比关系;②尽管节点处于高速移动之中，节点在收到时间交互分组后，仍然可以经过一段相对较长的时间，再进行回复，并保证时间同步的实现。这对无人机自组网的时间同步是非常重要的，因为无人机的数传速率有限，发送和接收时间交互分组的时间相对较长，节点在该时间内的移动会造成往返时延之差较大，引起同步误差。但是，从本小节的分析可以知道，只要将tpw限定在一个相对充裕的范围内，就不会影响时间同步的实现。

2.2.2 拓扑结构的改变

节点移动造成的另一个影响就是网络拓扑结构的改变，可分为以下两种情况:①一次时间信息交互完成以后，网络拓扑结构发生改变，此时各节点的邻居节点数目和组成发生改变，需要重新为各邻居节点分配加权系数;②在时间信息交互过程中网络拓扑结构发生改变，即节点A向节点B发送时间交互分组后，A和B之间的链路突然中断，B对A的回复无法到达A。

为此，本文采用随机生成加权系数的方式，只要每个节点都根据成功完成时间信息交互的邻居节点来随机生成加权系数并保证其和为1，就可以在一次交互后经过若干次迭代运算达到同步，而不受拓扑结构改变的影响。

表1 tpw与节点移动速度的关系

2.3 方案对时间记录误差的容忍度

在时间分组的交互过程中，对每个分组发送时间、接收时间的记录，都受到接收处理时延时间记录误差的影响。如图1，节点记录的时间ta、tb、tab、tba并非真正的分组发送和到达时间，而是在真实时间的基础上加上时间记录误差(包括硬件反应时间、接收处理时间和不稳定性等)。这样，由这几个时间计算得来的td、tΔ存在误差。下面研究该同步方案对时间记录误差的容忍程度。

假设各节点采用相同硬件记录时间分组交互时间，时间记录误差服从均值为0、方差为σ2的正态分布[12];完成粗同步的节点时钟偏差在350μs之内均匀。在同步过程中加入时间记录误差，并逐渐增大σ2，直到无法完成同步，得到不同同步精度要求下所允许的σ2的上限，如图5所示。从图5中可以看出，同步精度要求越高，对时间记录稳定度的要求就越高，当同步精度要求为10ns时，σ所允许的最大值为0.456μs;而当同步精度要求为100ns时，σ所允许的最大值可以达到4.390μs。当前，硬件的精度和稳定度已经达到了很高的水平，保证了该方案的可实现性。

2.4 时间同步速度

图6展示了完成粗同步的节点时间偏差在350μs之内均匀分布时，使用本文方案完成10ns和100ns精度的时间同步所需要的迭代运算次数。可以看到，在一次时间信息交互以后，经过很少的几次迭代，就能完成较高精度的时间同步;参与交互的节点数目越多，完成同步所需的迭代运算次数越少。

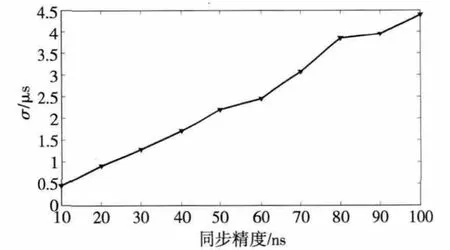
图5 方案对时间记录误差的容忍度

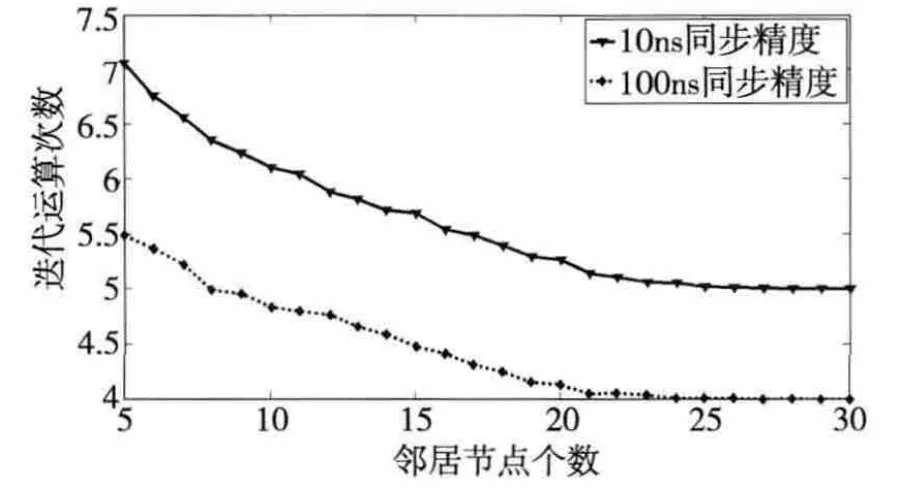
图6 时间同步速度

3 结束语

通过对动态、多跳网络的收敛性、节点移动的影响、时间记录误差容忍度等关键问题的详细研究探讨，并结合分析和仿真，证明本文提出的分布式时间同步方案可以用于无人机空中自组网，并能在较小的运算量条件下达到较高的同步精度。

[1]王 波，叶晓慧，赵玉亭，严雪丽.自组织网络时钟同步研究综述[J].计算机科学，2010，37(5):30～34.

[2]徐 倩，陈彦辉.自组织跳频组网网络同步技术研究[J].电子元器件应用，2007，9(5):56～58.

[3]董 超，田 畅，倪明放.Ad hoc网络时钟同步研究[J].通信学报，2006，27(9):110～117.

[4]胡志坚，张承学，杜志伟.基于 GPS的同步时钟的研制及其应用[J].小型微型计算机系统，2005，26(8):1433～1435.

[5]秦明伟，姚远程，李 云.网络时延测量中的时间同步系统应用研究[J].通信技术，2008，41(8):149～153.

[6]聂玉婷，高仲合.单向时延测量中的时间同步问题[J].通信技术，2009，42(10):125～127.

[7]杨 琦，石江宏，陈辉煌.无线自组织网络分布式时隙同步算法[J].系统工程与电子技术，2011，33(4):889～894.

[8]徐明霞，赵民建，董 芳，等.基于内部参数解析的Ad Hoc网络时隙同步[J].浙江大学学报(工学版)，2005，39(6):901～905.

[9]Schenato L，Gamba G.A Distributed Consensus Protoco for Clock Synchronization in Wireless Sensor Network[C].Proc.of 46th IEEE Conference on Decision and Control，2007:2289 ～2294.

[10]刘庆刚，李大双，朱家成.多跳TDMA组网同步的分布式控制方法[J].通信技术，2012，45(5):26～29.

[11]Gabriel A Puerta，Edgar A Aguerri.Effects of Topology and Mobility in Bio-inspired Synchronization of Mobile Ad Hoc Networks[C].IEEE Latin-American Conference on Communications，2010.

[12]燕洪成.传感器网络时间同步技术研究[D].中北大学，2011.