椭球转动惯量的计算及温度对其的影响

王 曈,程 钊,王 慧

(电子科技大学a.计算机科学与工程学院,b.物理电子学院,四川成都 611731)

椭球转动惯量的计算及温度对其的影响

王 曈a,程 钊a,王 慧b

(电子科技大学a.计算机科学与工程学院,b.物理电子学院,四川成都 611731)

利用微积分的基本知识,在推导出椭球体转动惯量的基础上,给出温度对椭球体转动惯量的影响.认为在一般情况下温度对一般类刚体材料的密度影响极小,可以忽略,在计算时可以考虑使用与温度无关的函数来表示密度,但在应用到工业等项目时,则需要考虑与其具体环境的变化相适应来选取函数计算.

微积分;转动惯量;椭球体;材料力学;温度

在《大学物理》中,讨论刚体绕定轴转动时,会引入转动惯量这一物理学名词.通常,一般教科书会列出几种常见刚体的转动惯量,再给出均质细杆、圆盘、圆环等的转动惯量推导的例题,球体的转动惯量基本不在推导范围之内[1].圆盘、圆环属于二维,球体属于三维,后者的推导较前者难度高了一个数量级,用微积分解决这一问题,是把数学知识用到物理中的具体过程.基于球体,椭球体转动惯量的推导尽管存在一些难度,还是可推出的.但在公式中,很明显可以得出,物体度量的密度函数对转动惯量有着影响,由此联想到温度对一般的材料有着影响这一事实,即温度对物体的密度函数有着影响[2].本文基于球体对椭球体转动惯量进行计算,并就温度对其产生的影响进行论述.

1 椭球体转动惯量的计算

这里引用广义的球坐标系进行计算[3].

为方便计算,直观理解,用Matlab对椭球体进行仿真如图1所示,对球坐标进行如下说明:

球坐标的定义采用通用的物理学定义,约定φ为天顶角,θ为方位角,l为原点到所在点的距离,同时采用坐标变换以方便计算.

将温度确定,得到在温度函数为常数T时的椭球密度函数为f(l,φ,θ,T)

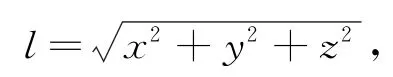
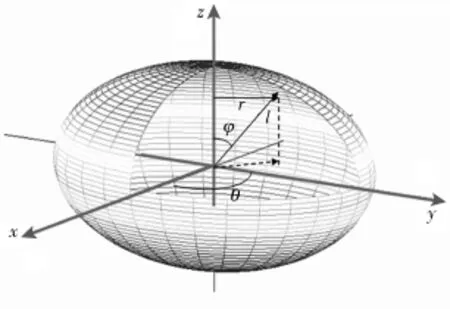
图1 椭球体展示图Fig.1 Ellipsoid show figure

对椭球方程在直角坐标系的表达式(为了方便书写,采用x′,y′,z′代替x,y,z)进行以下坐标变化:

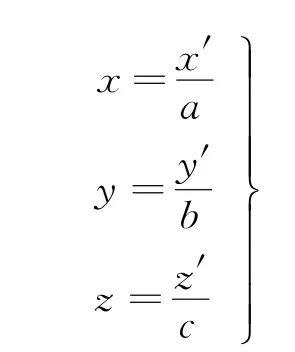
得到方程:

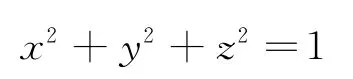
转动惯量的计算公式:

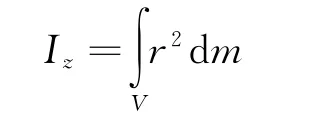
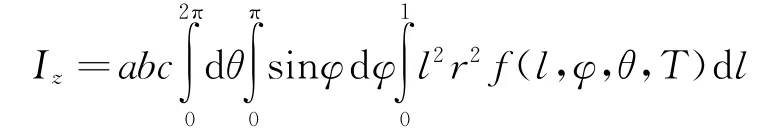
将直角坐标中转轴的长度化为球坐标下的表达形式:

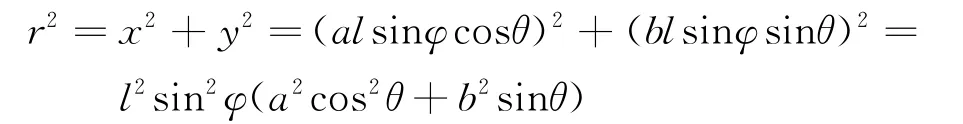
代入上式:

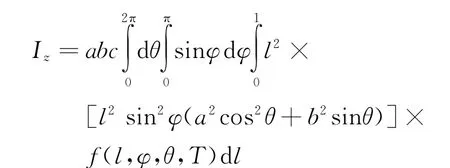
式中,关于质量与体积微元的关系:

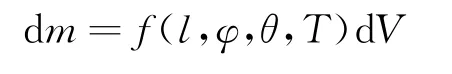
坐标变化(利用雅克比行列式):

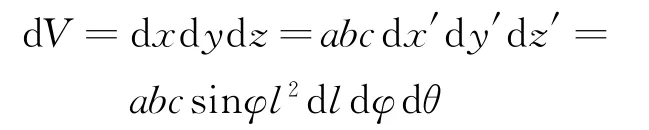
代入后得到如下表达式:

化简得:

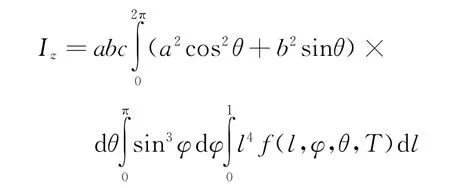
当密度恒为常数D时有:

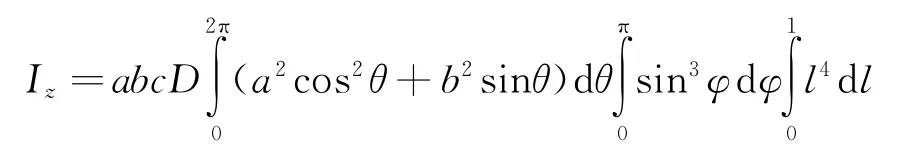
由微积分知识可得:

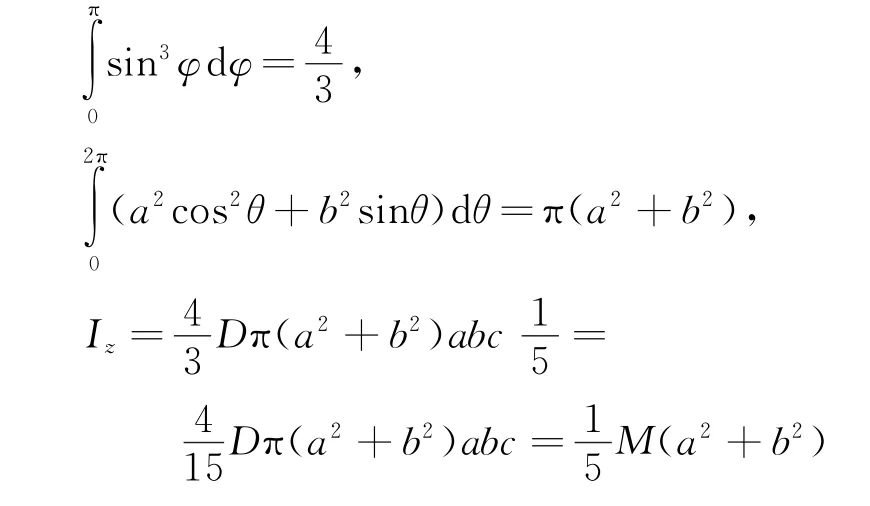
2 温度对材料密度D的影响

做初步讨论时,为了简化模型,认为椭球体上质量分布均匀,材料密度D为常数.温度及压力对固体密度有着一定的影响.此时在变化的环境中,椭球由刚体变成类刚体,在计算时应该考虑温度t对其影响.

图2为不同温度下没有施加振动时固体密度与压力曲线[45].从40℃时固体的密度比室温时提高很多,随着温度的升高,固体密度增大更快,当温度接近熔点时,只需较小的压力就能使固体的密度迅速升高至接近其真实密度.可见,温度升高物体更容易变形.由于这种影响,在旋转的过程中,椭球体的转动惯量会随之变化,整个椭球的形状发生改变,导致质量分布发生改变,此时,ρ也将变成温度、压强、角速度的函数ρ(t,p,ω),此时,刚体的转动惯量不再是常数,而是随着角速度ω变化的函数.

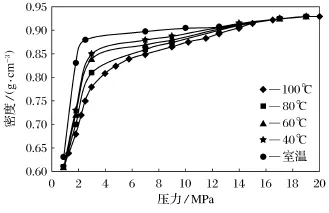
图2 不同温度下没有施加振动时固体密度与压力曲线Fig.2 Solid density and pressure curve in different temperatures without applying vibration

3 结 论

用广义球面坐标变换的方法对椭球体绕对称轴旋转的转动惯量进行了计算,改进了以往求其转动惯量的方法,避免了繁琐复杂的积分过程,用其本质解决了这一个问题.这种方法简单、实用,在工程实际中有很重要的应用价值.

温度对材料的影响大部分集中在常温或稍低于、高于室温的温度下,压力对材料的影响在0～8 MPa时变化明显.在一般情况下,我们所处的温度对一般类刚体材料的密度影响极小,可以忽略,所以在计算的时候可以考虑使用与温度无关的函数来表示密度.但在应用到工业等项目时,则需要考虑与其具体环境的变化相适应来选取函数计算,并结合其他因素如湿度、震动等其他相关因素.只有在考虑到各种情况下的实际物体的物理性质,并对其做出定量分析,才能使其理论具有存在的意义.

[1]滕保华,廖旭.大学物理学:上[M].北京:科学出版社, 2010:95113. (Teng Baohua,Liao Xu.University Physics:Vol.1[M]. Beijing:Science Press,2010:95113.)

[2]纳什.静力学与材料力学[M].北京:科学出版社,2002: 142 152. (Nash W.Statics and the Mechanics of Materials[M]. Beijing:Science Press,2002:142152.)

[3]赵新闻,杨兵初,黄生祥.椭球转动惯量的计算[J].物理与工程,2007,17(2):28 30. (Zhao Xinwen,Yang Bingchu,Huang Shengxiang. Calculation of the Rotary Inertia of Ellipsoid[J].Physics and Engineering,2007,17(2):2830.)

[4]徐芝纶.弹性力学[M].北京:高等教育出版社,2007:221241. (Xu Zhilun.Elastic Mechanics[M].Beijing:Higher Education Press,2007:221241.)

[5] 石宝山,瞿金平,周南桥,等.温度和振动力场对聚合物固体物料压实密度的影响[J].工程塑料应用,2006,34(7): 2831. (Shi Baoshan,Qu Jinping,Zhou Nanqiao,et al.Effect of Vibration Field and Temperature on Density of Polymer Solid Granules[J].Engineering Plastics Applications, 2006,34(7):2831.)

【责任编辑:王 颖】

Calculation of Rotary Inertia of Ellipsoid and Influence of Temperature

Wang Tonga,Cheng Zhaoa,Wang Huib
(a.School of Computer Science&Engineering,b.School of Physical Electronics,University of Electronic Science and Technology of China,Chengdu 611731,China)

Using the basic knowledge of differential and integral calculus,the moment of inertia of ellipsoid is deduced,and the influence of temperature on it is given.It is considered that the temperature on the general effect of the density of rigid material is minimal and it can be neglected; functions which are independent of temperature can be used to represent the density in calculating. However,when applied to industrial and other projects,when selecting function,whether it can adapt to specific changes in the environment need to be considered.

differential and integral calculus;moment of inertia;ellipsoid;mechanics of materials; temperature

2095-5456(2014)01-0084-03

O 313.3

A

2013 11 18

王 曈(1994),女(满族),辽宁沈阳人,电子科技大学学生;王 慧(1963),女,四川成都人,电子科技大学副教授.