雷诺数对后向台阶剪切层转捩特性的影响

周 宁

(北京航空航天大学 教育部流体力学重点实验室，北京100091)

迮 程

(中国空间技术研究院，北京100081)

潘 翀*

(北京航空航天大学 教育部流体力学重点实验室，北京100091)

流动的分离和再附普遍存在于航空航天、流体机械等实际工程中，是一类具有重要学术意义和应用价值的流动现象.二维后向台阶具有最简单的几何外形，但同时包含了分离再附流动的所有重要特征和细节，因此常被作为研究分离再附流动的理想简化模型.一般而言，流动的分离可分为两种[1]:由逆压梯度驱动产生的分离和由几何形状突变产生的分离.后向台阶流动属于后者，边界层在台阶角点处分离，在台阶下游形成自由剪切层.小雷诺数下，边界层在分离时维持层流状态，上方主流区和下方静止流区间的较大速度梯度使得剪切层对特定小扰动线性失稳，这一不稳定性属于对流不稳定性的范畴[2－3]，扰动在自由剪切层中沿流向增长，使得自由剪切层逐渐向湍流状态过渡，同时卷出离散的大尺度展向涡，称为层流分离剪切层转捩[4－5].

后向台阶流动常被用于研究湍流分离—再附[6－7]及其引起的传质、传热[8]和压力脉动[9－10]问题，各种分离流动控制技术也主要应用在湍流分离—再附问题上[11].相比之下，后向台阶层流分离剪切层研究[12－13]中的旋涡结构[14－15]不可忽视，与之相关的转捩问题的研究相对较少，且主要集中在理论研究方面.传统的线性稳定性分析可以用来解决剪切层开始失稳的临界雷诺数问题[3，16]，近年来也开始使用非模态稳定性分析和瞬态增长理论来预测扰动在剪切层中的非正则增长[2].最近，Schäfer等使用直接数值模拟(DNS，Direct Numerical Simulation)对转捩剪切层的拍动特性进行了详细研究[17]，他们发现剪切层和再附点的拍动源于自由剪切层中的大尺度旋涡与回流区中回流旋涡的涡－涡相互作用.这种从涡演化角度出发的研究方法为研究剪切层的转捩特性和机制提供了新的思路.基于此，本文将以实验方式研究二维后向台阶分离流动的转捩特性，主要研究雷诺数的变化对转捩剪切层中扰动早期放大以及旋涡结构演化的影响，并初步探讨转捩点位置随雷诺数变化的规律.

1 实验设备及方法

1.1 实验装置

本实验在北京航空航天大学回流式有机玻璃水槽中进行.水槽实验段尺寸为4 800 mm×600 mm×600 mm(长×宽×高).水槽侧壁为有机玻璃，顶部不封顶，从侧向进行观测和拍摄.采用垂直布置的伺服电机作为水循环动力，可实现水流流速从0～200 mm/s范围内连续调节.实验段流场品质良好、流动均匀，实验段湍流度Tu约为0.8%，实验平均水温25℃，对应黏度系数 ν=0.893 mm2/s.实验模型为外流式后向台阶，如图1所示，台阶前缘为长短轴比8∶1的椭圆.台阶前缘距后缘800 mm.实验所用台阶高度分别为30，20，10 mm.台阶的最小展高比达到20，可以认为几何形状满足二维要求，同时坐标系定义如图1所示，流动显示所在平面与台阶后缘上角点相交处定义为原点，流向为x向，壁面外法向为y向.

图1 实验模型示意图

1.2 测量显示技术

使用二维时间连续PIV系统对后向台阶流动的侧视(x－y)平面进行速度场测量.功率2 W的连续激光器输出激光片光照亮台阶中轴面，使用高速CCD相机记录粒子图像，CCD相机分辨率为640像素 ×480像素，对应视野范围80 mm×60 mm，使用2台CCD相机沿流向并排布置同步测量，以扩大视野范围.粒子为空心玻璃微珠，粒径约20μm，在粒子图像上的平均成像直径大于2像素.通过改变自由来流速度U∞和台阶高度H来改变雷诺数ReH.对于每一个ReH，以100Hz的采样频率采样3次，每次连续采样1万帧粒子图像，对应的总采样时间为300 s.粒子图像对的时间间隔为10ms，粒子在图像上的最大位移不超过7像素.使用多重网格迭代变形算法[18]解析粒子图像对，最终查询窗口是16像素×16像素，重叠率75%，得到的速度场的空间分辨率是0.5 mm/像素.本实验测速的不确定度约为1%，由此计算脉动速度强度(速度的二阶统计量)的不确定度约为5% ～8%.考虑到本实验自由来流速度(U∞=40～85mm/s)较低以及自由剪切层的高能频率集中在低频区范围，PIV的采样频率(100Hz)足够解析自由剪切层中的动力学特征，同时采样样本足够多，能够获得收敛的流场脉动强度特性.

2 实验结果及分析

2.1 时均流线及剪切层发展

图2给出的是雷诺数ReH=2844时的时均流向速度分布图.连接流场中时均速度为零(=0)的点得到零线，时均速度为零的点的高度随流向位置增加不断下降.零线即为剪切层上方主流区和下方诱导区的分界线.连接每一流向位置的最大负涡量zmax出现位置得到最大剪切线.随流向位置的增长，平均涡量的展向分量z的集中性越来越差，沿展向逐渐扩张，并且向壁面靠近.涡量的这种发展趋势可以用剪切层的厚度发展来刻画.剪切层的厚度沿程逐渐增加，剪切层向壁面弯曲[13].仿照半射流宽度的定义，定义涡量为当地流向位置处50%zmax的位置为剪切层的上下边界，如图2中粉色线所示.

图2 流场速度示意图ReH=2844

在时均化后的流场中时均回流涡顺时针旋转，出现在一次回流区[19]，位于最大剪切线下方.上游出现二次回流区，表现为逆时针方向旋转的二次分离涡，尺度明显较小.分离剪切层的再附位置xre可以根据零线与下壁面的交点确定.另外，二次分离区与一次回流区的分界点为二次分离点，二次分离点流向位置xss由当地流线的拓扑形态来确定.

为了分析不同雷诺数下的流场形态，图3中绘制出4个不同雷诺数下时均流线图，可以看到不同流场的二维后向台阶下游时均流场具有的不同结构特征.当到达台阶之前，流线平行于壁面，经过台阶之后，上游来流的流线逐渐向下壁面靠近，而在下壁面和上游来流流线之间会存在分离泡和回流区.具体来看，当ReH=2844时，可以清晰地观察到顺时针旋转的分离泡和靠近台阶尺度较小的逆时针旋转的二次回流区.当 ReH=2392时，依然能够很清晰地看到顺时针旋转的分离泡和逆时针旋转的二次涡，并且在二者之间存在着三次分离区.此外，可以定性地观察到再附点的位置xre随着雷诺数的减小而后移.当ReH=1790时，一次分离泡很明显，而二次涡尺度减小，再附点位置xre继续后移.而二次分离点的位置xss变化与之不同，随ReH的增大表现为先后移再前移的趋势.另外，当ReH=1 032时，相较于以上雷诺数出现了很大的不同，分离泡延展至台阶和下游很远，形状非常狭长，二次回流区已经观察不到，同时再附点xre大大后移.受篇幅限制，其他雷诺数下的流线图不再给出.

图3 不同雷诺数下时均流线图

2.2 再附点和二次分离点

上游来流在台阶角点处发生分离脱离壁面，经过一段时间后会重新再附到下游壁面.后向台阶是由几何形状产生的强制分离，分离点固定即为台阶角点.而另外一个特征点再附点的位置不固定，而且会随雷诺数而改变.关于再附点的位置定义在之前的研究中出现了许多种方法.本文中将零线与下壁面的交点确定为再附点的位置xre.定义分离泡和二次回流区的分界点为二次分离点，二次分离点在壁面的位置为xss.

通过对18个不同工况下再附点的位置变化，发现无论是台阶高度还是上游来流速度均会对再附点的位置产生影响.图4中黑色线为再附点的位置xre随雷诺数ReH的变化规律.可以看到随雷诺数的增大，再附点的位置xre逐渐前移，并且前移的幅度逐渐减小，而当雷诺数大于2 500之后，再附点的位置达到饱和，稳定在4.7左右.图中还画出了二次分离点的位置xss随雷诺数ReH的变化，随雷诺数的增长，二次分离点的位置xss先后移再前移，且在ReH=1790左右，二次分离点的位置xss达到最大值.

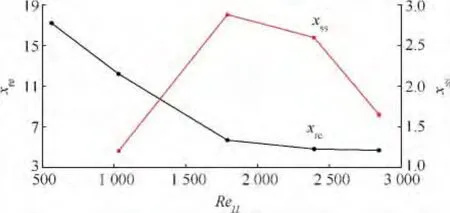
图4 再附点位置xre和二次分离点位置xss随雷诺数的变化

2.3 扰动增长

脉动特性为后向台阶流动具备的重要特性，不同的流动结构将对脉动量产生不同的影响.对脉动量的分析将能更好地帮助理解流场中扰动发展的情况和剪切层转捩的特点.文献[20]通过直接数值模拟对后向台阶流动的扰动增长进行了详尽的研究，是本文研究的基础.

扰动的发展在到达相应再附点之前呈增大的趋势，到达再附点之后开始下降.相关文献指出，在K－H(Kelvin－Helmholtz)不稳定机制的作用下，扰动增长的早期阶段呈现典型的指数增长趋势，在对数坐标下可以应用直线斜率拟合来计算扰动的增长，而后期则表现为非线性增长，两者之间分界点即为线性增长的结束点.本文将针对之前获得的在多个雷诺数下由二维时间解析PIV测量得到的平面速度场的数据库进行深入分析，研究分离剪切层在转捩过程中的扰动放大问题.本文的重点是在二维后向台阶流动中分析无量纲化后的湍流度Tu和雷诺应力分量随流向的发展特点.

上式兼顾了流向/法向脉动分量，但限于二维测速技术，没有考虑展向脉动分量.为了衡量剪切层内的总体扰动水平，引入剪切层内的当地平均值:

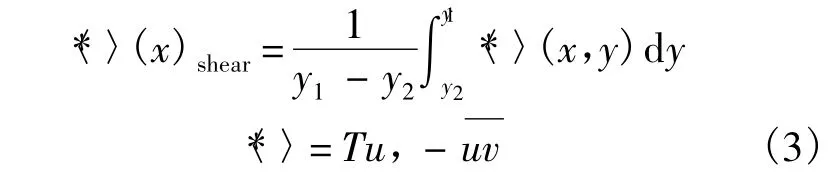
从定量分析角度来说，对于一段已知指数增长的散点，可以采取拟合的方法，拟合公式为y=ceax+b.已知扰动初期为指数增长，因此在对数坐标下将表现为线性增长.图5对应于雷诺数为ReH=2844时湍流度增长拟合曲线通过拟合得到的直线，直线的斜率即为湍流度指数增长的空间放大率.

图5 湍流度发展情况，ReH=2844

在对18个工况下的扰动情况分别进行拟合后，得到不同流速不同台阶高度所对应的湍流度和雷诺应力的初始指数增长的空间增长率随雷诺数的变化如图6所示.湍流度增长率随雷诺数的增大表现为先增大后稳定的趋势:当雷诺数从500开始增加到2500左右，湍流度的初始放大率变化非常大，表现为显著提高，即说明在此区间湍流度的增长对雷诺数非常敏感，而当雷诺数大于2500后，湍流度的增长趋于稳定.

与湍流度增长变化类似，绘制出雷诺应力分量的空间增长率随雷诺数的变化如图7所示，随雷诺数的增大，雷诺应力的空间增长率一直保持着对雷诺数ReH的敏感性，随之不断增大.

图6 湍流度空间增长率随雷诺数的变化

图7 雷诺应力空间增长率随雷诺数变化

2.4 转捩点位置

本文主要以实验方法研究雷诺数是对后向台阶流动分离剪切层转捩位置的影响.分离后的层流剪切层往往经过K－H不稳定性演化阶段发展为湍流状态.在雷诺数较小的情况下，剪切层再附到壁面之后转捩为湍流状态，随雷诺数的增大，转捩过程将提前到再附之前发生.在本文雷诺数研究范围内，转捩均在再附之前发生.在本实验中，上游来流为层流，而在后向台阶下游中会转捩为湍流，因此转捩在何处发生，即转捩点的流向位置xtr的研究显得非常必要.Lian和Shyy研究低雷诺数翼型背风面分离泡时指出，可以将无量纲雷诺切应力超过10－3的位置认为是转捩开始点[20]，Burgmann 和 Schröder还提出另一种转捩开始点的判别准则，将无量纲雷诺切应力开始脱离线性增长的位置作为转捩开始点[21].

根据上述两种方法，对每个雷诺数下的转捩点位置xtr均作出统计，结论如图8所示，可以看出，虽然两种方法计算得到的转捩点位置xtr的具体数值有差别，但是二者随雷诺数的变化趋势一致，随雷诺数的增大，转捩点的位置xtr逐渐前移，并且当雷诺数大于2 500后，转捩点的位置xtr稳定在0.8左右.这与再附点xre的变化规律相吻合.这也与之前的研究结果相吻合[3，16].

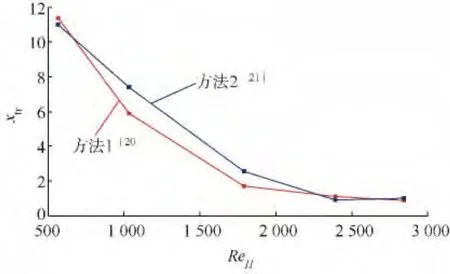
图8 转捩点位置随雷诺数的变化

考虑到再附点xre也和ReH呈现出类似的负相关特征，单纯使用xtr并不能量度转捩开始点在整个脱体流区中的相对位置，因此使用无量纲参数xre/xtr，它间接描述了转捩前流区在整个脱体流区中的比例.如图9所示，图中黑色方块为根据上述方法1计算所得到的转捩点位置，红色空心圈为计算得到的xre/xtr，红色虚线为对无量纲参数xre/xtr随雷诺数ReH变化的拟合直线.可以发现，xre/xtr随ReH线性增加，说明转捩开始点在自由剪切层中的相对位置与雷诺数呈严格的反比函数关系，也就是说，随ReH的增大，转捩开始点前移的幅度要大于再附点的前移幅度.

图9 转捩开始点位置xtr与xre/xtr随雷诺数的变化

3 结论

本文运用粒子图像测速技术，根据二维时间解析PIV测量得到的流动速度场进行的对流动时均性和脉动性，对比不同雷诺数下的流场形态差异以及讨论相同雷诺数下流场参数特征两种手段，得到的具体结论如下:

1)在本文的雷诺数研究范围内，再附点的位置xre随雷诺数的增大而前移，并逐渐稳定在4.7左右.二次分离点xss随雷诺数的增大表现为先后移再前移.

2)扰动的发展在到达相应再附点之前呈增大的趋势，湍流度Tu和雷诺应力分量的初期增长基本遵循y=ceax+b.同时发现，湍流度Tu和雷诺应力分量的空间增长率均整体呈现随雷诺数增大而增大的基本趋势.

3)在本文工况范围内，当雷诺数较小时转捩开始点位置xtr对雷诺数非常敏感，随雷诺数的变化较大;当雷诺数大于2500后，雷诺数变化的影响达到饱和，转捩点位置xtr稳定在0.8左右.同时，再附点位置与转捩点位置之比xre/xtr随雷诺数呈线性增长，说明转捩开始点在自由剪切层中的相对位置与雷诺数呈严格的反比函数关系.即随雷诺数增大，转捩点的相对位置随之提前.

References)

[1]Simpson R L.Turbulent boundary－layer separation[J].Annual Review of Fluid Mechanics，1989，21(1):205 －232

[2]Blackburn H M，Barkley D，Sherwin S J.Convective instability and transient growth in flow over a backward－facing step[J].Journal of Fluid Mechanics，2008，603:271 －304

[3]Kaiktsis L，Karniadakis G E，Orszag S A.Unsteadiness and convective instabilities in two－dimensional flow over a backward－facing step[J].Journal of Fluid Mechanics，1996，321:157 －187

[4]Armaly B F，Durst F，Pereira J C F，et al.Experimental and theoretical investigation of backward－facing step[J].Journal of Fluid Mechanics，1983，127:473 －496

[5]Sinha S N，Gupta A K，Oberai M N.Laminar sepaprating flow over backsteps and cavities，part I:backsteps[R].AIAA Journal，1981，19(12):1527 －1530

[6]Le H，Moin P，Kim J.Direct numerical simulation of turbulent flow over a backward－facing step[J].Journal of Fluid Mechanics，1997，330:349 －374

[7]王晋军，连淇祥.后向台阶湍流边界层分离、再附及发展[J].航空学报，1994，15(4):393 －398

Wang Jinjun，Lian Qixiang.Turbulent boundary layer separation，reattachment and redevelopment over a backward－facing step[J].Acta Aeronautica et Astronautica Sinica，1994，15(4):393－398(in Chinese)

[8]Mehrez Z，Bouterra M，El Cafsi A，et al.The influence of the periodic disturbance on the local heat transfer in separated and reattached flow[J].Heat and Mass Transfer，2009，46(1):107 －112

[9]Chun S，Liu Y Z，Sung H J.Wall pressure fluctuations of a turbulent separated and reattaching flow affected by an unsteady wake[J].Experiments in Fluids，2004，37(4):531 －546

[10]Liu Y Z，Kang W N，Sung H J.Assessment of the organization of a turbulent separated and reattaching flow by measuring wall pressure fluctuations[J].Experiments in Fluids，2005，38(4):485－493

[11]Chun K B，Sung H J.Control of turbulent separated flow over a backward－facing step by local forcing[J].Experiments in Fluids，1996，21(6):417 －426

[12]王晋军，连淇祥.后向台阶层流边界层分离实验研究[J].北京航空航天大学学报，1993，19(1):52－56

Wang Jinjun，Lian Qixiang.An experimental investigation on laminar boundary layer separation over a backward－facing step[J].Journal of Beijing University of Aeronautics and Astronautics，1993，19(1):52 － 56(in Chinese)

[13]兰世隆，王晋军.后向台阶层流分离剪切层特性研究[J].北京航空航天大学学报，1996，22(5):581－584

Lan Shilong，Wang Jinjun.The characteristics of separated shear layer in a backward－facing step laminar flow[J].Journal of Beijing University of Aeronautics and Astronautics，1996，22(5):581－584(in Chinese)

[14]齐鄂荣，黄明海，李炜，等.应用PIV进行二维后向台阶流流动特性的研究(1):二维后向台阶流的旋涡结构的研究[J].水动力学研究与进展:A 辑，2004，19(4):525－532

Qi Erong，Huang Minghai，Li Wei，et al.Investigation of vortex structure of the 2D backward facing step flow via PIV[J].Journal of Hydrodynamics，2004，19(4):525 －532(in Chinese)

[15]齐鄂荣，黄明海，李炜，等.二维后向台阶流流动特性的实验研究[J].实验力学，2006，21(2):225－232

Qi Erong，Huang Minghai，Li Wei，et al.An experimental study on the 2D time－average flow over a backward facing step via PIV[J].Journal of Experimental Mechanics，2006，21(2):225－232(in Chinese)

[16]Fortin A，Jardak M，Gervais J J，et al.Localization of Hopf bifurcations in fluid flow problems[J].International Journal for Numerical Methods in Fluids，1997，24(11):1185 －1210

[17]Schäfer F，Breuer M，Durst F.The dynamics of the transitional flow over a backward－facing step[J].Journal of Fluid Mechanics，2009，623:85 －119

[18]Scarano F，Riethmuller M L.Advances in iterative multigrid PIV image processing[J].Experiments in Fluids，2000，29(1):51－60

[19]Boiko A，Dovgal A，Hein S，et al.Particle image velocimetry of a low－Reynolds－number separation bubble[J].Experiments in Fluids，2011，50(1):13 － 21

[20]Lian Y S，Shyy W.Laminar－turbulent transition of a low Reynolds number rigid or flexible airfoil[R].AIAA Journal，2007，45(7):1501－1513

[21]Burgmann S，Schröder W.Investigation of the vortex induced unsteadiness of a separation bubble via time－resolved and scanning PIV measurements[J].Experiments in Fluids，2008，45(4):675－691