利用非等距灰色理论方法判定失效机理一致性
2014-11-05李晓钢王亚辉
李晓钢 王亚辉
(北京航空航天大学 可靠性与系统工程学院,北京100191)
随着科学技术的发展,高可靠、长寿命产品越来越多,这使得加速试验技术越来越受到重视.加速试验通过提高应力水平快速激发产品缺陷、加速产品失效过程,以在较短时间内得到产品的失效或退化信息,并结合加速方程,通过高应力下产品的寿命和可靠性,外推正常应力下产品的寿命和可靠性.为了保证这种推断结果的准确性,产品在正常应力和加速应力下必须具有相同的失效机理[1-4].因此,对加速试验失效机理一致性的研究是很有必要的.
目前,国内外判定加速试验失效机理一致性的方法主要分为2大类:第1类是在试验完成之后,基于数据处理和试验观察的方法进行失效机理的一致性检验.主要包括:基于加速模型参数不变的方法[5-6]、基于统计的方法[7-8]及基于试验观察的方法[9].这些方法的缺点是:均为加速试验做完之后的验证,无法在加速试验之前进行识别从而指导加速试验设计.第2类是在加速试验之前,根据强化试验、预试验等数据对失效机理的边界条件进行确定.文献[10-11]提出了利用灰色理论来确定产品失效机理一致性边界条件的方法,根据强化试验或预试验的数据,结合灰色理论的预测方法,给出了失效机理一致性判定的方法和流程,进而指导加速试验的设计.但是,该方法也有缺点,即必须规定用于灰色理论模型的建模数据是等间距的.由于在强化试验或预试验中进行步进试验时,采用等步长的施加应力,若取的步长稍大,会影响预测结果的精度,不能准确地找到产品失效机理突变点;取的步长过小,会使试验的时间及费用增加.因此,利用灰色理论来确定产品失效机理一致性边界条件时,采用等间距的预试验数据是不合适的.
对产品进行加速试验时,初始施加应力阶段是不会改变产品的失效机理的,因此,在进行预试验时,要先预估一下可能的失效机理突变点,开始可以适当地扩大施加应力的间距,随着施加应力的变大再缩小间距,这样可以获得更多的高应力下产品的退化或失效信息,以便准确地识别失效机理边界条件.本文提出了基于非等间距GM(1,1)模型的失效机理一致性识别方法,建立非等间距的GM(1,1)预测模型,并和等维新息模型结合,计算模型的残差,依据残差的突变确定失效机理的变化点.
本文分别以某型号光电编码器和加速度计为例,设计对比试验,对非等间距的GM(1,1)预测模型和等间距的预测模型进行对比分析,发现在170℃时,光电编码器的失效机理已经发生改变;在105℃时,加速度计的失效机理已经发生变化,表明用非等间距预试验数据更加合理.根据相对误差的大小,证明了非等间距GM(1,1)灰色理论一致性检验的精度较高.
1 理论分析
1.1 基于非等间距GM(1,1)的灰色预测模型
GM(1,1)模型是灰色理论的一个重要分支,是最常用的一种定量灰色预测.设预试验中得到的性能退化序列为
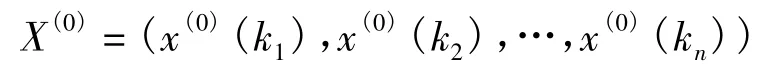
相邻分量之间的间距为
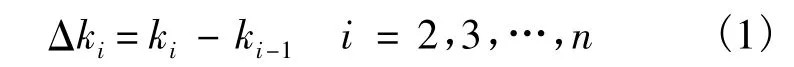
若Δki为常数,则称序列X(0)为等间距序列;若Δki是一个变化的值,则称X(0)为非等间距序列.
对X(0)进行一阶累加生成,将原始序列的第1个数据作为生成列的第1个数据,将原始序列的第2个数据加到原始序列的第1个数据上,其和作为生成列的第2个数据,将原始序列的第3个数据加到生成列的第2个数据上,其和作为生成列的第3个数据,按此规则进行下去,便可得到生成列[12]:
由一阶生成模块X(1)建立一阶线性微分方程模型为
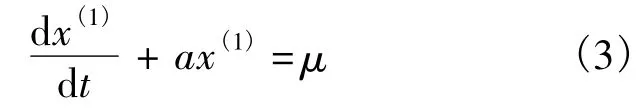
式中,a为发展灰数,反映了性能退化序列X(0)和一阶累加性能退化序列X(1)的发展趋势;μ为内生控制灰数,反映了数据间的变化关系.
灰色微分方程为

式中 z(1)(ki+1)为 X(1)在[ki,ki+1]上的背景值.
因为方程(3)的解为指数形式,所以利用指数曲线近似法,可以构造出背景值z(1)(ki+1),具体证明方法可以参考文献[13].

对式(4)用矩阵形式表示:

应用最小二乘法求解待估参数,即
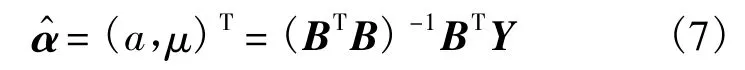
根据参数a和μ的估计值,可以求方程(3)的离散解,即时间响应函数.可求出一阶累加性能退化序列X(1)的预测模型为

对式(8)进行累减还原,可得到原始性能退化序列的预测模型为

1.2 等维新息灰色预测模型[14]
等维新息灰色预测模型是一种对传统灰色GM(1,1)预测模型的改进.在灰色系统中,后期观测数据与前期观测数据存在着密切的关系,且距某观测时刻越近的前期观测数据,所包含的预测新息越多.在用等维新息结合灰色GM(1,1)模型预测时,先用灰色GM(1,1)模型预测一个值,将其补充到已知数据之后,去掉最老的一个数据,保持数列等维,再建立灰色GM(1,1)模型预测下一个值,将其结果补充到数列之后,去掉最老的一个数据,依次建模.等维新息预测效果比较好,因为每次换入的是系统的实际数据,用实际数据来调整模型.
在预测前,必须确定模型的维度,为使模型精度达到最高,可选维度一般为4~11维,最佳维度的选择可以通过数值试验来确定,即分别选用各个维度对各个点进行预测,然后与各个点的实际值进行比较,相对误差最小的就是要选择的最佳维度.
1.3 模型的残差、相对误差
根据建立的预测模型,对各个点的值进行预测,结合预测值和实际观测值计算残差和相对误差.灰色GM(1,1)模型的残差和相对误差的计算公式[7]如下.
残差:

相对误差:

1.4 基于非等距灰色理论的一致性判定方法
利用非等间距的灰色GM(1,1)模型,对预试验数据进行预测,将各个点的预测值和观察值进行比较,计算残差,观察残差是否发生显著变化,若在某点发生显著变化,说明产品的发展趋势在该点发生了改变,产品已经发生了质的变化,也就可认为此时产品的失效机理发生了变化.同时,还可以计算出预测点的相对误差,根据相对误差的大小确定模型的精度.
2 应用实例
实例1 在与某单位合作开展某型号卫星天线驱动机构上的光电编码器的寿命和可靠性研究中,为了能够准确地评估其可靠性寿命,在加速试验之前,首先要对光电编码器进行预试验,然后利用非等间距灰色GM(1,1)模型对预试验数据进行处理、预测,找到失效机理一致性的边界条件.为了证明本文提出的基于非等间距GM(1,1)模型失效机理一致性判定方法的有效性,设计了对比试验,具体如下.
分别对m,n两组样品进行高温步进试验,以光敏三极管的信号幅值为测试的性能参数.
m组以等步长进行高温步进试验,具体施加温度应力为:95,105,115,125,135,145,155,165,175,185℃.
n组以不等步长进行高温步进试验,具体施加温度应力为:95,125,145,155,160,165,170,175,180,185℃.
试验开始前,常温下测量样品的性能参数,作为试验中比较基准.试验过程中每一步长停留时间为1 h,前10 min内为保温阶段,后50 min初始和末端各测量一次性能参数.预试验的数据如表1所示.

表1 光电编码器两组预试验数据
根据等维新息模型,通过数值试验,选择最佳维度为4,利用等间距灰色GM(1,1)模型和非等间距灰色GM(1,1)模型对预试验数据进行建模,计算出发展灰数a和内生控制灰数μ,如表2所示.两组预试验对应的信号幅值预测值、残差及相对误差如表3、表4所示.作出两组预试验残差值的曲线图,如图1、图2所示.

表2 两组试验各数据段的发展灰数和内生控制灰数
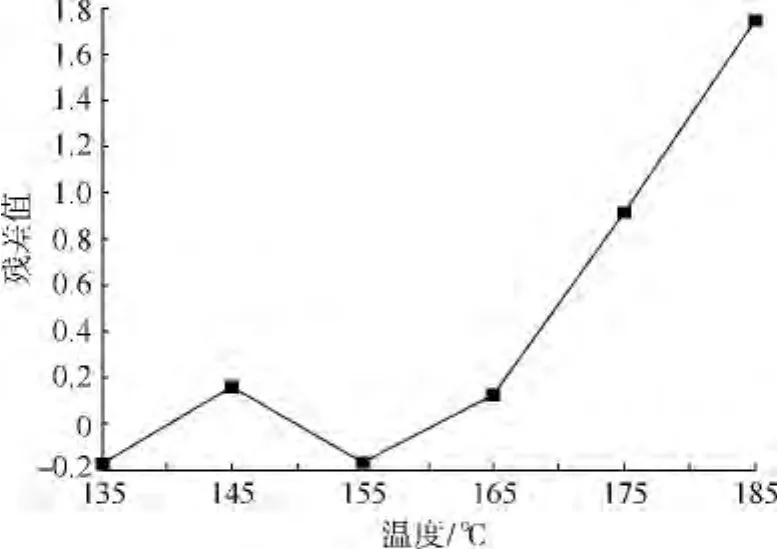
图1 m组各温度应力下的残差值
从图1中可以看出,残差值在175℃时发生了显著的变化,可以确定当温度达到175℃时,产品的失效机理发生了变化.

图2 n组各温度应力下的残差值
从图 2中可以看出,残差值在 160,165,170℃时是不断下降的,但是,在160,165℃时,残差值还在0附近,当温度升高到170℃时,残差值明显偏离了零,且随着温度的升高残差值与零的偏移距离还在增大,所以可以确定产品在170℃时,产品的失效机理已经发生了变化.
对两组预试验在165,175,185℃的相对误差进行对比分析,表明利用非等间距灰色GM(1,1)预测的相对误差比利用等间距灰色GM(1,1)预测的相对误差小,所以,基于非等间距GM(1,1)模型的失效机理一致性识别方法精度较高.
实例2 以某装备惯性导航系统中的加速度计为例,设计对比的预试验,分别以等间距的灰色GM(1,1)模型和非等间距的灰色GM(1,1)模型对预试验数据进行加速失效机理一致性的判定.
对加速度计进行高温步进应力试验,起始温度为50℃,分k,l两组进行,一组以等步长进行,另一组以非等步长进行.在实验过程中,每一步停留1 h,以确保加速度计的温度达到热平衡后对其进行功能测试,测试参数主要是标度因数K1和零偏K0.以零偏K0为例进行失效机理的一致性判定,具体的对比预试验温度应力如表5所示.

表5 加速度计的两组预试验 ℃
根据等维新息模型,通过数值试验,选择最佳维度为4,利用等间距灰色GM(1,1)模型和非等间距灰色GM(1,1)模型对预试验数据进行建模,计算出零偏发展灰数a,如表6所示.两组预试验对应的信号幅值预测值、残差及相对误差如表7、表8所示.作出两组预试验残差值的曲线图,如图3、图4所示.

表6 K0各数据段的发展灰数

表7 k组K0的预测值、观测值、残差及相对误差

表8 l组K0的预测值、观测值、残差及相对误差

图3 k组各温度应力下的残差值
从图3中可以看出,K0的残差值在第6个点发生了显著的变化,因此可以认为K0的发展趋势在第6个点发生了突变,第6个点对应的温度是110℃,即失效机理在110℃的时候发生了变化.
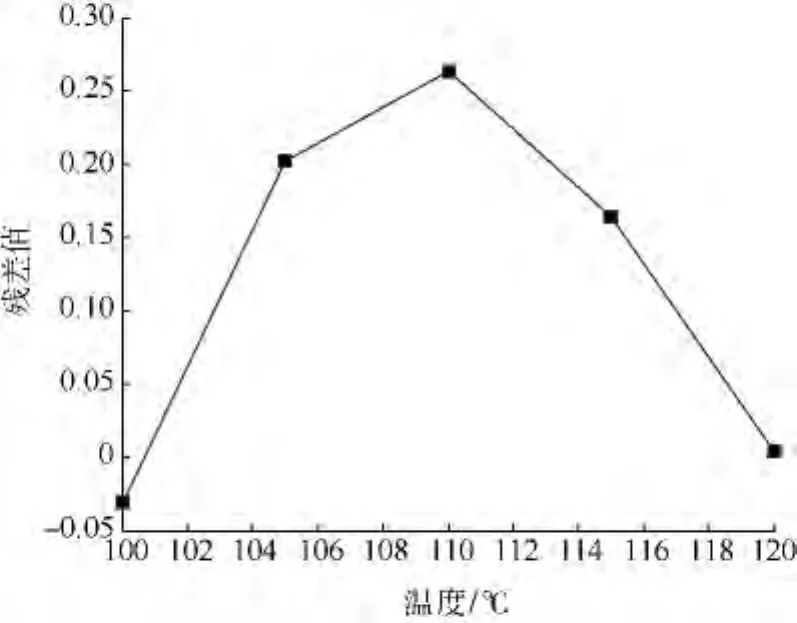
图4 l组各温度应力下的残差值
由图4可以看出,K0的残差值在第6个点发生了显著变化,可以认为K0的发展趋势在第6个点发生了突变,而此时第6个点对应的温度是105℃,即失效机理在105℃的时候发生了变化.
对加速度计两组对比的预试验在100,110,120℃的相对误差进行对比分析,表明利用非等间距灰色GM(1,1)预测的精度较高.通过以上分析证明了利用非等间距灰色GM(1,1)模型进行失效机理一致性判定的有效性.
3 结论
1)本文给出了一种基于非等间距灰色理论的失效机理一致性判定方法,与传统的基于数据处理和试验观察的一致性检验方法相比,此方法仅需利用少量预试验数据就可对失效机理进行一致性判定;
2)与基于等间距灰色理论方法相比,可以获得更多的高应力下产品的退化或失效信息,从而进一步提高了预测精度;
3)在预试验中,利用非等距的应力施加方式更加合理,提高了试验效率,有较强的工程适用性和通用性.
References)
[1]Nelson W.Accelerated life testing-step-stress models and data analyses[J].IEEE Transactions on Reliability,1980,29(2):103-108
[2]郭春生,谢雪松,马卫东.加速试验中失效机理一致性的判别方法[J].半导体学报,2006,27(3):560 -563
Guo Chunsheng,Xie Xuesong,Ma Weidong.A failure-mechanism identification method in accelerated testing[J].Chinese Journal of Semiconductors,2006,27(3):560 -563(in Chinese)
[3]Hu J M,Barker D B,Dasgupta A,et al.Role of failure-mechanism identification in accelerated testing[C]//Proceedings of the Annual Reliability and Maintainability Symposium.Piscataway,NJ:IEEE,1992:181 -188
[4]Chen M L,Tseng S T.Optimal design for step-stress accelerated degradation tests[J].IEEE Transactions on Reliability,2006,55(1):59-66
[5]Pan X X,Huang X K,Chen Y X,et al.Connotation of failure mechanism consistency and identification method for accelerated testing[C]//Prognostics and System Health Management Conference.Piscataway,NJ:IEEE,2011:1 -7
[6]王前程,陈云霞,邓沣鹂,等.加速计加速退化机理一致性边界确定方法[J].北京航空航天大学学报,2012,38(11):1512-1516
Wang Qiancheng,Chen Yunxia,Deng Fengli,et al.Approach of determining accelerated degradation mechanism consistency’s boundary for accelerometers[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(11):1512 - 1516(in Chinese)
[7]Nelson W.Analysis of accelerated life test data-part I:the arrhenius model and graphical methods[J].Transactions on Electrical Insulation,1971,6(4):165 -181
[8]冯静.基于秩相关系数的加速贮存退化失效机理一致性检验[J].航空动力学报,2011,26(11):2439 -2444
Feng Jing.Consistent test of accelerated storage degradation failure mechanism based on rank correlation coefficient[J].Journal of Aerospace Power,2011,26(11):2439 -2444(in Chinese)
[9]Kim J,Yoon D,Jeon M,et al.Degradation behaviors and failure analysis of Ni-BaTiO3base-metal electrode multilayer ceramic capacitors under highly accelerated life test[J].Current Applied Physics,2010,10(5):1297 -1301
[10]姚军,王欢,苏泉.基于灰色理论的失效机理一致性检验方法[J].北京航空航天大学学报,2013,39(6):734 -738
Yao Jun,Wang Huan,Su Quan.Consistency identification method of failure mechanism based on grey theory[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(11):734-738(in Chinese)
[11]潘晓茜,康锐.基于灰色预测的加速试验机理一致性判定方法[J].北京航空航天大学学报,2013,39(6):787 -791
Pan Xiaoxi,Kang Rui.Identification method of failure mechanism consistency for accelerated testing based on grey forecasting[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(6):787 -791(in Chinese)
[12]杨林泉.预测与决策方法应用[M].北京:冶金工业出版社,2011
Yang Linquan.The method application of forecasting and decision-making[M].Beijing:Metallurgical Industry Press,2011(in Chinese)
[13]戴文战,李俊峰.非等间距GM(1,1)模型建模研究[J].系统工程理论与实践,2005,9(2):89-93
Dai Wenzhan,Li Junfeng.Modeling research on non-equidistance GM(1,1)model[J].System Engineering-Theory &Practice,2005,9(2):89 -93(in Chinese)
[14]赵玲,许宏科.基于等维新息灰色马尔科夫模型的互联网用户人数预测研究[J].计算机科学,2013,40(4):119 -121
Zhao Ling,Xu Hongke.Research on internet users number prediction based on equal dimension and new information grey Markov model[J].Computer Science,2013,40(4):119 - 121(in Chinese)
