基于状态条件概率的设备剩余寿命预测

张继军 邓 力 马登武 曹文静

(海军航空工程学院，烟台264001)

机载设备是飞机武器装备系统的重要组成部分，其性能的好坏直接影响到飞机的作战效能.机载设备剩余使用寿命预测是飞机故障预测与健康管理的重要内容，是设备视情维修中制定维修策略的重要依据，因此，一直是该领域研究的热点问题，同时也是难点问题.剩余使用寿命是指设备在正常的使用条件下(不加维修)，从被检测的某一时刻起到其失效时的时间长度[1]，它不仅依赖于设备的当前状态，还依赖于到该时刻为止所获得的设备的历史数据与状态信息.

目前，基于状态的剩余使用寿命预测方法主要有基于物理的方法和基于经验的方法[2].基于物理的方法，由于具备设备特定的物理模型，一般不需要大量同类设备的历史数据即可获得较精确的寿命预测结果.但是，对于复杂的电子设备，建立其完备的物理模型往往非常复杂[3]，甚至不可能实现.基于经验的方法，又称基于数据驱动的方法，思想是直接从状态监测数据(包括同类电子设备的历史数据)出发，采用各种理论方法预测设备的剩余使用寿命.基于经验的方法主要有:①基于状态预测/外推的方法，如神经网络法[4]、随机滤波法[5]、支持向量机[6]等;②基于统计回归的方法，如基于隐马尔科夫模型(HMM，Hidden Markov Model)/隐半马尔科夫模型(HSMM，Hidden Semi-Markov Model)的方法[7－8]、时间序列分析法[9－10]、比例风险模型[11]等.

一般来讲，采用设备的退化状态数据能够准确地实现剩余寿命的预测，但是在实际的状态监测过程中，设备的真实状态信息隐藏于观测数据中，加之各种不确定性因素的影响，往往很难获得精确的状态数据，如果使用这些不精确的状态信息进行剩余寿命预测，精度会受到较大的影响.针对上述情况，本文首先引入状态条件概率对HMM进行不确定性改进;然后以比例风险模型为基础建立设备的剩余使用寿命模型，并将状态条件概率作为其中的协变量，以期降低不确定性因素对寿命预测的影响，提高预测精度;最后以飞机发动机的重要电子附件——温控放大器为应用对象验证了本文模型的有效性.

1 HMM的不确定性改进

HMM是一种描述双重随机过程统计特性的概率模型[12－13]，一个随机过程是描述状态转移的有限状态的Markov链，另一个随机过程描述每个状态和观测值之间的统计对应关系，描述如下:

1)N:模型中状态的数目，记t时刻Markov链所处的状态为qt∈{1，2，…，N};

2)M:每个状态对应的可能的观测值数目，记t时刻观测到的观测值为ot;

3)π:初始状态概率矢量，π=(π1，π2，…，πN)，πi=P(q1=i)，1≤i≤N;

4)A:状态转移概率矩阵，A=(aij)，aij=P(qt+1=j|qt=i)，1≤i，j≤N;

5)B:观测值概率矩阵，B=(bj(ot))，bj(ot)=P(ot=vk|qt=j)，或记为bj(k).

因此，一个HMM可以简约地记为λ=(π，A，B).

本文采用比例风险模型解决机载设备剩余使用寿命预测问题，而该模型是基于退化状态的，由于受到噪声、各种误差等不确定性因素的影响，退化状态本身也具有一定的不确定性.为了解决这一问题，引入状态条件概率分布矢量描述退化状态的不确定性.

定义1在HMM中，已知模型参数λ和至时刻 t 时的观测值序列 o1，o2，…，ot，系统在时刻 t处于状态i的概率称为状态i的条件概率，记为，则0，称为系统在t时刻的状态条件概率矢量.当t=0时，规定π0=π.

式中

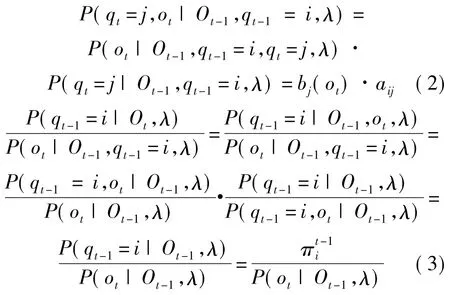
式(3)中的分母部分，结合式(2)的计算结果有

将式(2)～式(4)代入式(1)中可得

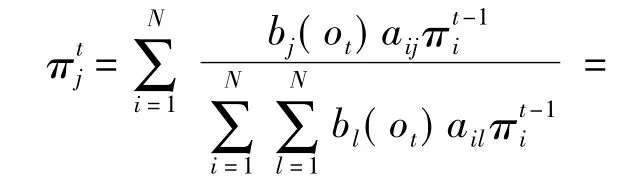
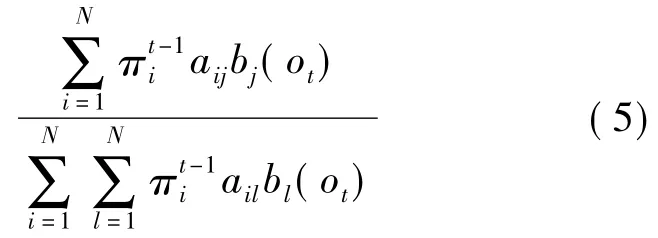
2 机载设备剩余使用寿命模型

2.1 模型假设

文献[14]在推导可靠度函数时假设检测周期足够短，使得状态退化转移发生在检测时刻附近，这在实际应用中(尤其是对于军用设备)是不可行的.因此，本文作如下假设:

1)设备的状态退化过程满足HMM条件;

2)实施维修前，状态退化过程是不可逆的;

3)检测周期是固定的，但受工作条件和环境因素的影响，状态发生退化转移的时刻是随机的;

4)设备在每个检测周期内最多发生一次状态退化转移.

2.2 状态退化转移时间的确定

用{1，2，…，N}表示设备的退化状态，并且在每一个检测点Δ，2Δ，…，设备的状态可通过HMM获得.记kΔ时刻对应的退化状态为i，状态条件概率矢量为.从状态条件概率矢量的定义以及Viterbi算法确定状态的原理可知，此时有，且在状态 i 向状态j转移前后，逐渐减小，逐渐增大，所以是单调递增的(i＜j＜N).因此，可以通过的大小判断状态退化转移的时间，具体如下:

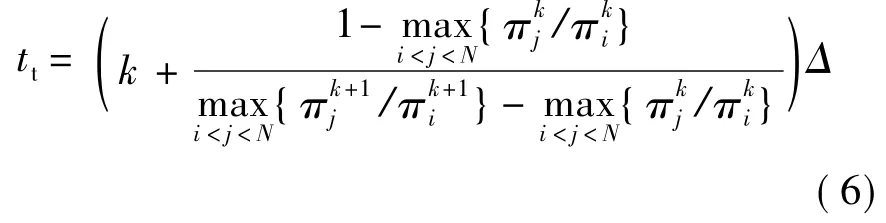
2.3 基于状态条件概率的可靠度函数

本文采用威布尔比例风险模型建立可靠度函数.威布尔比例风险模型形式如下[15]:

式中，h(t，Z)为故障率;h0(t)是仅与时间有关的基本故障率;Z为协变量，与设备退化状态相关;γ为回归参数，表示协变量Z对故障率的影响;β为威布尔分布的形状参数;η为威布尔分布的尺度参数.

设备的条件可靠度可以描述为:已知k个检测时刻和对应的退化状态，设备在第k个检测时刻之后无故障工作时间t的概率.可以看出，设备的退化状态对其条件可靠度有直接的影响.

设备的退化状态是由各种因素共同决定的，每种因素的影响都反映在退化状态上.在比例风险模型中，现有文献有的是将其中某些起主要决定作用的因素作为协变量[15－16]，有的直接将设备的退化状态作为协变量[14].前者忽略了部分因素的影响，后者在确定设备的退化状态时存在不确定性，都会导致一定的误差.本文将设备的状态条件概率作为协变量，一方面，状态条件概率能够比较精确地反映设备退化状态的相关信息;另一方面，从其计算过程可知，状态条件概率能够充分利用历史状态信息，有效减少不确定性因素的影响.

在kΔ时刻，设备的状态为i，则γZk的具体表达式写为

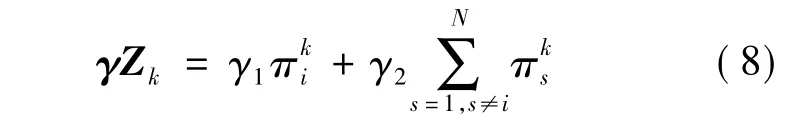
于是，条件可靠度函数可记为R(t，Zk，k)=R(t，πk，k).下面推导其表达式.

由式(8)可知，影响R(t，πk，k)的是kΔ时刻的状态信息和时间t内因状态转移而改变的状态信息，所以，只需要判断状态转移的时间而不必关心(k+1)Δ时刻的状态以及时间t与间隔Δ的长短关系.记状态转移时刻为tt.

1)若tt≥kΔ+t，即时间 t 内不发生状态转移，有[14]

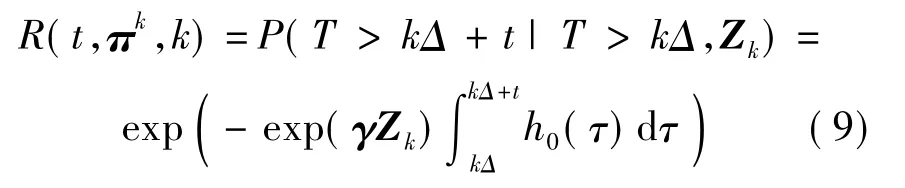
式中T为随机故障时间.

2) 若 kΔ＜tt＜kΔ + t，即时间 t内发生状态转移，有

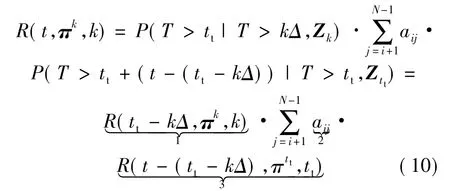
式(10)中的3部分含义如图1所示.其中2和3两部分之所以求和，是因为状态j有可能是i+1与N－1之间的任一状态，N为故障态，不予考虑.

图1 时间t内发生状态转移情况示意图

3)若tt≈kΔ，即，则有

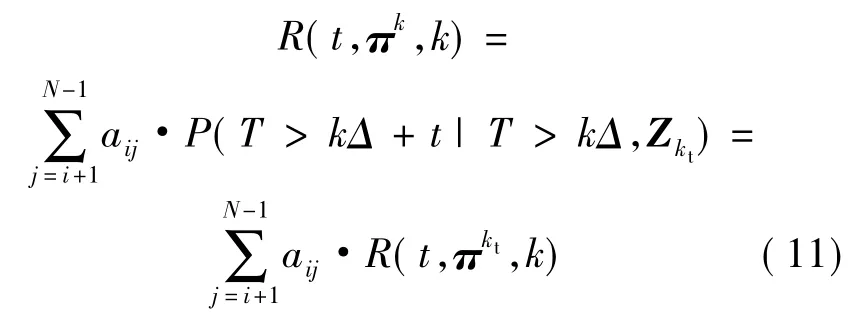
式中的Zkt表示转移后的状态j，相应的 γ Zkt的具体表达式为

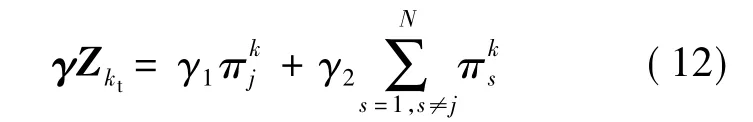
综上所述，设备的条件可靠度函数表示如下:

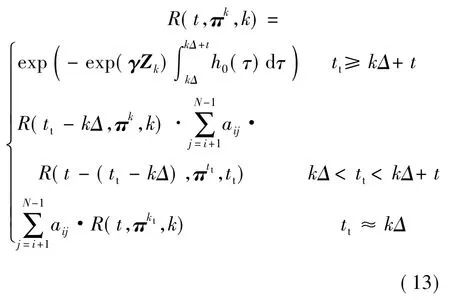
2.4 剩余使用寿命模型

机载电子设备的剩余使用寿命是指从检测时刻kΔ起，直至设备发生故障不能工作的时间长度 t ，记为 LRUL(t，πtk，k).根据可靠性理论中可靠度与剩余寿命的关系，机载电子设备的剩余使用寿命模型如下:

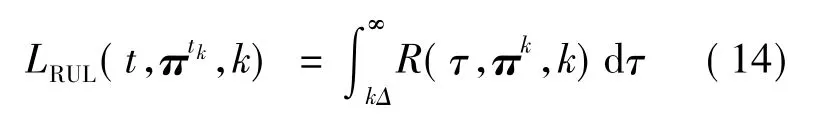
通过前面的推导过程可以看出，上述剩余使用寿命模型能够充分利用设备的历史数据和状态信息减少不确定性因素带来的影响.对于模型中的参数Ω(β，η，γ)，本文采用极大似然估计法[15]进行估计.

3 实例计算

飞机发动机温控放大器是发动机上一个非常重要的附件，其性能好坏直接影响发动机能否正常工作，但由于安装位置和工作环境等原因造成本身成为故障多发部件，故对其进行剩余寿命预测是非常必要的.温控放大器虽然是一个小部件，但同时也是一个复杂的电子产品，属于电子设备一类，因此，对其进行研究具有一定的代表性.按照温控放大器性能退化的不同程度，设定其状态数为5，包括正常态、故障态和3个中间退化状态，对应的HMM模型选为左-右型右转模型，如图2所示.观测值数目设为5.

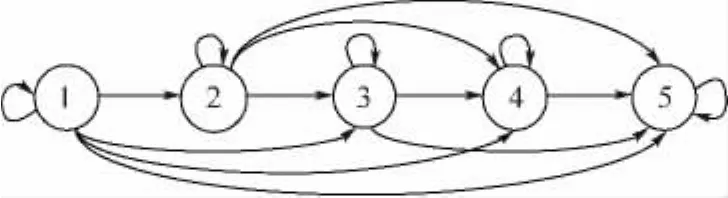
图2 HMM状态转移模型

3.1 数据处理

选为研究对象的某型温控放大器共计20台，其中失效12台，截尾8台.选取反映其性能的T1，T3和T6温度信号电压、T6失速警告电压等4项参数为仿真数据对象，如表1所示，限于篇幅只列出部分数据.

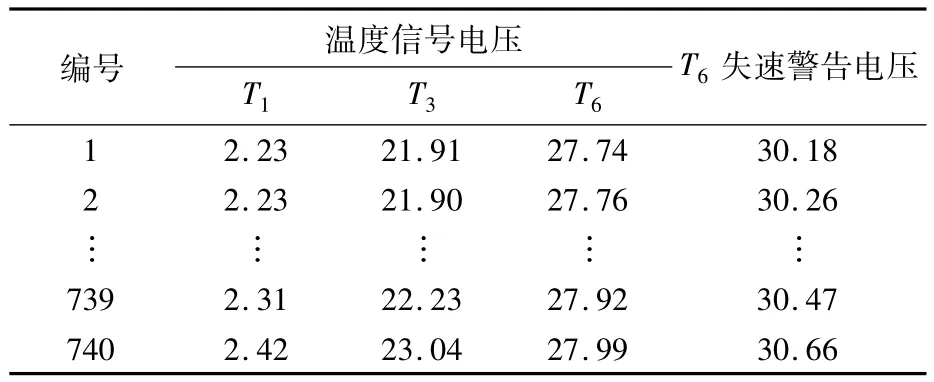
表1 设备状态退化数据 mV

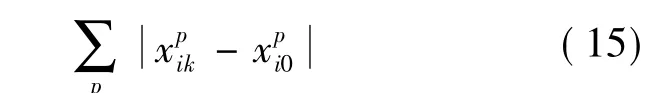
为第k个检测时刻4项参数的绝对变化量之和.本文将式(15)得到的融合数据作为仿真计算数据.

3.2 计算结果及分析

3.2.1 参数估计

采用极大似然估计法得到的剩余使用寿命模型各参数的值分别为:β=1.67，η=45.8，γ1=0.41，γ2=0.17.检测周期 Δ=2飞行小时(fh).HMM的参数由多智能体遗传算法估计得到[17]:

根据20台温控放大器的检测数据，可计算得到不同状态在接近退化转移之前的取值范围[0.895 2，1)，因此，将阈值确定为 C =0.9.

3.2.2 剩余使用寿命预测

预测过程中所需要的设备退化状态信息采用最小二乘支持向量机(LS-SVM)和HMM组合的方法进行估计与预测[17](限于篇幅不再详述).为了证明本文方法的有效性，另将设备的退化状态直接作为协变量构建剩余使用寿命模型[14]，进而对两种模型的预测结果进行比较.其剩余寿命模型形式与本文相同，只是γZ的表达式如下:

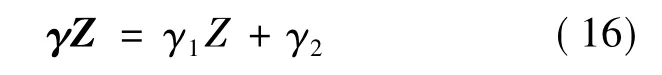
式中，Z为设备的退化状态;γ1=－γ2=0.5.

某台温控放大器的实际故障时间为93.6fh，两种模型分别记为M1(本文模型)和M2，随机选取4个检测点进行预测，结果如表2所示，其中，预测误差取绝对值.从结果可以看出，模型M1的预测精度明显高于模型M2的预测精度，而且随着检测时刻的推移，M1的预测精度逐渐提高，而M2则不具备此性质.这是因为随着设备服役时间的增长，获得的设备性能数据量增多，数据越多越能反映设备的性能状态退化信息，本文方法将状态条件概率作为协变量，是在降低不确定性因素影响的基础上，充分利用设备的历史数据进行剩余使用寿命预测，因此，能够获得逐渐提高的预测精度.相反，模型M2直接将退化状态作为协变量，由于未考虑不确定性因素的影响，预测精度相对较低.

表2 剩余使用寿命预测结果

同时，从预测结果还能看出，模型M1的预测值要低于实际值，这是一个比较理想的结果.因为从维修保障决策的角度来看，这一结果作为维修决策的参考依据时，能够避免重大事故的发生，是视情维修所需要的.模型M2的预测值高于实际值，不宜将其作为维修决策依据.另外，对其余11台失效的温控放大器进行剩余使用寿命预测后，本文方法的平均预测误差为9.3045%，并且预测值均低于实际值;而M2的预测值均高于实际值，平均预测误差为12.511%.

对于截尾的温控放大器，实际剩余使用寿命未知，任选其中一台作为计算对象，两种模型在6个未来检测点的预测结果如图3所示.可以看出，模型M1的预测值明显低于模型M2的预测值，而且相对平稳.综合对两种模型特点的分析，本文方法得到的预测结果应该更合理可信，完全可以作为维修保障的决策依据.

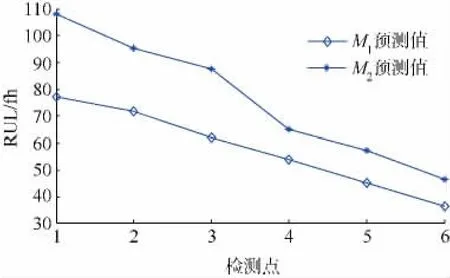
图3 剩余使用寿命预测结果

4 结论

本文引入状态的条件概率矢量对HMM进行不确定性改进，借以解决实际应用中不确定性因素的影响问题.本质上，这一改进是对HMM本身隐含的不确定性处理能力进行了显现和增强.在此基础上建立了基于状态条件概率的剩余使用寿命模型，并进行了实例仿真计算，结果表明本文方法具有如下特点:

1)预测精度高，而且随着设备检测数据的增多，预测精度逐渐提高;

2)预测值均低于实际值，可以作为维修保障的决策依据，理论上能够减少或避免欠维修现象的发生.

基于上述特点，本文方法具有较高的应用价值.但是，仍存在一定的缺点，即不能给出预测值的置信度，这将是后续研究的重点.

References)

[1]陈丽，牛晓磊，贾云献，等.基于状态信息的条件剩余寿命建模研究[J].系统工程与电子技术，2008，30(12):2516－2518

Chen Li，Niu Xiaolei，Jia Yunxian，et al.Study in conditional residual life modeling based on condition information[J].System Engineering and Electronics，2008，30(12):2516－2518(in Chinese)

[2]孟光，尤明懿.基于状态监测的设备寿命预测与预防维护规划研究进展[J].振动与冲击，2011，30(8):1－11

Meng Guang，You Mingyi.Review on condition-based equipment residual life prediction and preventive maintenance scheduling[J].Journal of Vibration and Shock，2011，30(8):1－11(in Chinese)

[3]Luo J H，Pattipati K R，Qiao L，et al.Model-based prognostic techniques applied to a suspension system[J].IEEE Transactions on Systems，Man，and Cybernetics-Part A:Systems and Humans，2008，38(5):1156－1168

[4]Tian Z G，Wong L，Safaei N.A neural network approach for remaining useful life prediction utilizing both failure and suspension histories[J].Mechanical Systems and Signal Processing，2010，24(5):1542－1555

[5]Carr M J，Wang W B.Modeling failure modes for residual life prediction using stochastic filtering theory[J].IEEE Transactions on Reliability，2010，59(2):346－355

[6]张磊，李行善，于劲松，等.基于关联向量机回归的故障预测算法[J].系统工程与电子技术，2010，32(7):1540－1543

Zhang Lei，Li Xingshan，Yu Jinsong，et al.Fault prognostic algorithm based on relevance vector machine regression[J].System Engineering and Electronics，2010，32(7):1540－1543(in Chinese)

[7]Chinnam R B，Baruah P.Autonomous diagnostics and prognostics in machining processes through competitive learning driven HMM-based clustering[J].International Journal of Production Research，2009，47(23):6739－6758

[8]方甲永，肖明清，周越文，等.电子产品动态损伤最优估计与寿命预测[J].仪器仪表学报，2011，32(4):807－812

Fang Jiayong，Xiao Mingqing，Zhou Yuewen，et al.Optimal dynamic damage assessment and life prediction for electronic products[J].Chinese Journal of Scientific Instrument，2011，32(4):807－812(in Chinese)

[9]王立，李晓阳，姜同敏.基于退化量分布时序分析的产品寿命预测[J].北京航空航天大学学报，2011，37(4):492－498

Wang Li，Li Xiaoyang，Jiang Tongmin.Life prediction of product based on degradation amount distribution time series analysis[J].Journal of Beijing University of Aeronautics and Astronautics，2011，37(4):492－498(in Chinese)

[10]崔建国，赵云龙，董世良，等.基于遗传算法和ARMA模型的航空发电机寿命预测[J].航空学报，2011，32(8):1506－1511

Cui Jianguo，Zhao Yunlong，Dong Shiliang，et al.Life prognostics for aero-generator based on genetic algorithm and ARMA model[J].Acta Aeronautica et Astronautica Sinica，2011，32(8):1506－1511(in Chinese)

[11]Liao H T，Zhao W B，Guo H R.Predicting remaining useful life of an individual unit using proportional hazards model and logistic regression model[C]//Proceedings-Annual Reliability and Maintainability Symposium.Piscataway，NJ:IEEE，2006:127－132

[12]Rabiner L R，Huang B H.An introduction to hidden Markov models[J].IEEE Signal Processing Magazine，1986，3(1):4－16

[13]Lee J M，Kim S J，Hwang Y，et al.Diagnosis of mechanical fault signals using continuous hidden Markov model[J].Journal of Sound and Vibration，2004，27(6):1065－1080

[14]Ghasemi A，Yacout S，Ouali M S.Evaluating the reliability function and the mean residual life for equipment with unobservable states[J].IEEE Transactions on Relibility，2010，59(1):45－54

[15]丁锋，何正嘉，訾艳阳，等.基于设备状态振动特征的比例故障率模型可靠性评估[J].机械工程学报，2009，45(12):89－94

Ding Feng，He Zhengjia，Zi Yanyang，et al.Reliability assessment based on equipment condition vibration feature using proportional hazards model[J].Journal of Mechanical Engineering，2009，45(12):89－94(in Chinese)

[16]蔡改改，陈雪峰，陈保家，等.利用设备响应状态信息的运行可靠性评估[J].西安交通大学学报，2012，46(1):108－112

Cai Gaigai，Chen Xuefeng，Chen Baojia，et al.Operating reliability assessment by equipment response condition information[J].Journal of Xi’an Jiaotong University，2012，46(1):108－112(in Chinese)

[17]张继军，张金春，马登武，等.基于改进HMM和LS-SVM的机载设备故障预测研究[J].海军航空工程学院学报，2012，27(6):645－650

Zhang Jijun，Zhang Jinchun，Ma Dengwu，et al.Fault forecast of airborne equipments based on improved HMM and LS-SVM[J].Journal of Naval Aeronautical and Astronautical University，2012，27(6):645－650(in Chinese)