基于RoeM格式思想的激波稳定格式构造

屈 峰 阎 超 于 剑 仲崇岩

(北京航空航天大学 国家计算流体力学实验室，北京100191)

随着计算流体力学(CFD，Computational Fluid Dynamics)需求的日益发展，人们对通量格式计算精度的要求也日益提高.1959年，俄罗斯科学家Godunov提出了基于Riemann精确解的一阶计算格式[1].理论与实践表明，它的解对于守恒型标量方程而言，满足熵条件且具有保单调性质和总变差不增的总差不减(TVD，Total Variation Diminishing)性质，并一定是物理解.因此该格式引起了广泛的注意.自此之后，许多构思精妙的通量格式雨后春笋般接连问世并极大促进了CFD的发展.而在这众多格式中，目前世界上公认性能最为优秀并被广泛应用的有Jameson的中心格式[2]、Roe的通量差分(FDS，Flux Difference Splitting)格式[3]、van Leer的矢通量分裂(FVS，Flux Vector Splitting)格式[4]、Liou 的对流上风分裂(AUSM，Advection Upstream Splitting Method)格式[5]及在其构造基础上衍生的一系列格式如AUSM+[6]，SLAU2[7]，AUSM+UP[8]等.尽管在实际应用中上述格式均表现出较为良好的特性，其依然因为各自构造思想中的“bug”而距离人们理想中的“完美”格式相距甚远.如van Leer的FVS格式无法精确捕捉接触间断，黏性分辨率较差;Roe的FDS格式在计算高速流动时会出现“粉刺”现象且对定常无黏通量的计算不满足焓守恒条件;Jameson的中心格式和AUSM+UP需要根据实际问题人工设置经验参数等[9].2010年，Kitamura等人通过一系列的数值实验得出结论[10]:目前已有的格式在高超声速计算中依然无法得到准确可靠的气动热结果.而影响其计算精度的因素有格式的激波稳定性、总焓守恒性、黏性分辨率.Kim等人通过对奇偶失联问题的理论分析，将Roe格式进行改进得到了RoeM类格式[11]，计算结果表明，RoeM类格式在保持Roe格式黏性分辨率高、鲁棒性强等优点的基础上避免了“粉刺”现象的出现并保持了定常无黏通量计算的总焓守恒.但是格式构造过程中，Kim等人仅简单地通过计算相邻网格格心处的压强比来判断该处是否有激波.这在较为简单的流动计算中尚不会造成影响，但在较为复杂的流动模拟中会因非物理情况的出现而导致其可靠性降低.为了克服这一问题，本文利用Jiang提出的光滑指示因子法来判断激波位置[12]，在 RoeM 格式的基础上构造了 RoeMW1，RoeMW2格式.下文的相关分析将表明，这两种格式均满足以下特点:

1)无需通过设置经验性参数就可保证其通量函数的激波稳定性;

2)黏性分辨率高，接触间断捕捉精确;

3)在高速定常流的计算中保证总焓守恒;

4)膨胀区计算时鲁棒性较强，无膨胀激波出现.

1 控制方程与计算方法

1.1 NS方程有限体积的一般形式

考虑如下三维双曲守恒律组:

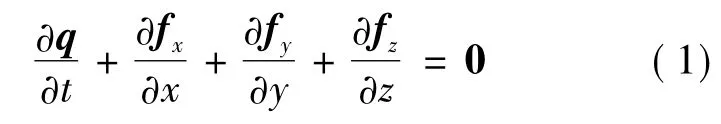
定义空间单元为

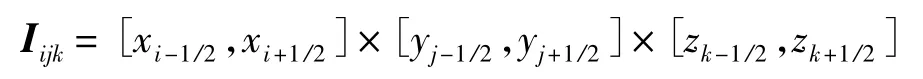
在单元Iijk上对式(1)进行积分，整理得

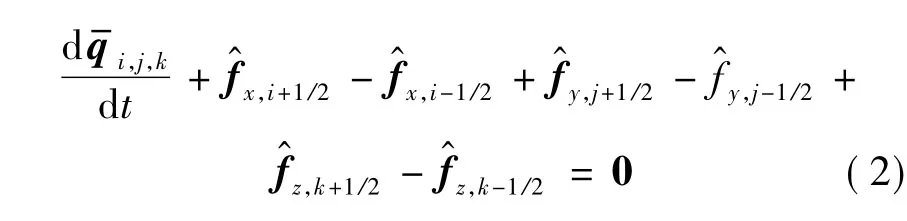
其中

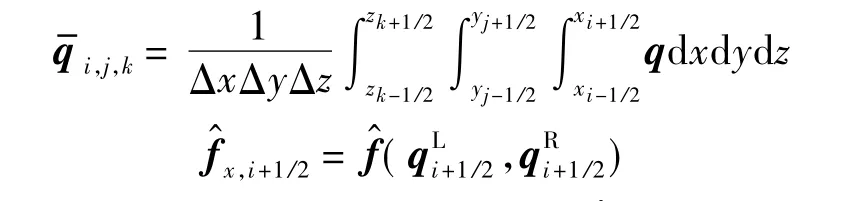
1.2 RoeMW类格式的构造

迎风类通量格式的数值质量通量均可由式(3)表示.

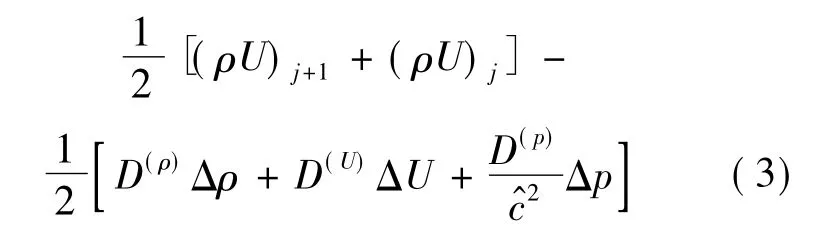
2000 年，Liou[13]发现式(3)中 D(p)的存在会导致Roe格式在计算超声速流动时容易出现“粉刺”现象.文献[14]也得到类似的结论.而文献[11]通过理论分析得出D(ρ)的大小亦影响着此格式的激波稳定性.为了平衡质量通量在数值计算中压强梯度对密度耗散的影响，D(p)可取为以下形式:

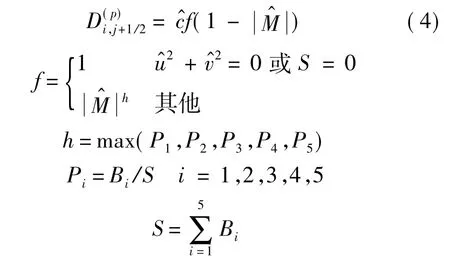
其中Bi采用文献[12]提出的形式，即

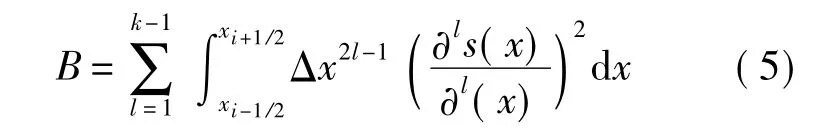
式中，s(x)为插值函数;k表示精度.实际计算表明，k的取值大小对最终计算结果影响不大.因此，考虑到计算效率的问题，在这里取k=2.即

后面的算例结果表明，在大部分情况下，该处理足以抑制“粉刺”现象的发生.但在某些情况如高速非定常流动的计算中，它可能因为压强扰动与密度扰动之间的平衡难以保证而出现激波不稳定现象.为了解决这一问题，本文在上述处理的基础上再利用函数f来加强对密度扰动的耗散.其具体形式如下:

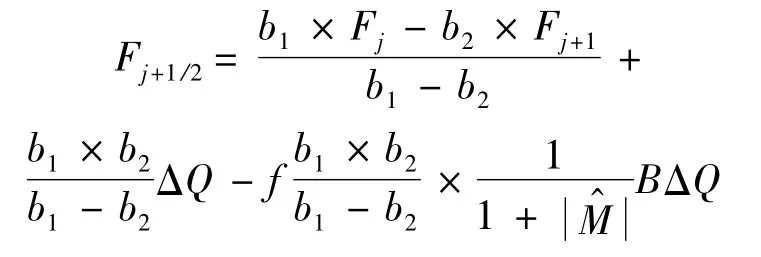
众所周知，无黏定常流计算中Roe格式不能保证总焓守恒的特性.根据Jameson在文献[15]中给出的结论，焓守恒格式的连续性方程和能量方程需满足如下形式:

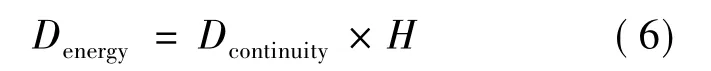
同时，为了消除Roe格式在实际计算时经常出现的“膨胀激波”现象，本文借鉴HLLEM[16]格式以及AUSM+[6]的构造思想将上式稍作修正，其具体形式如下:

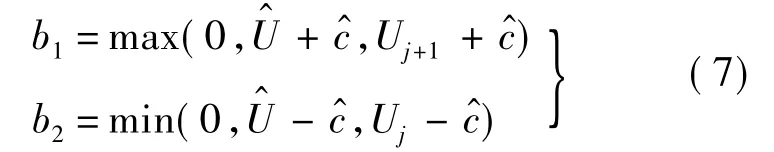
综上所述，本文所得格式的最终形式如下所述:

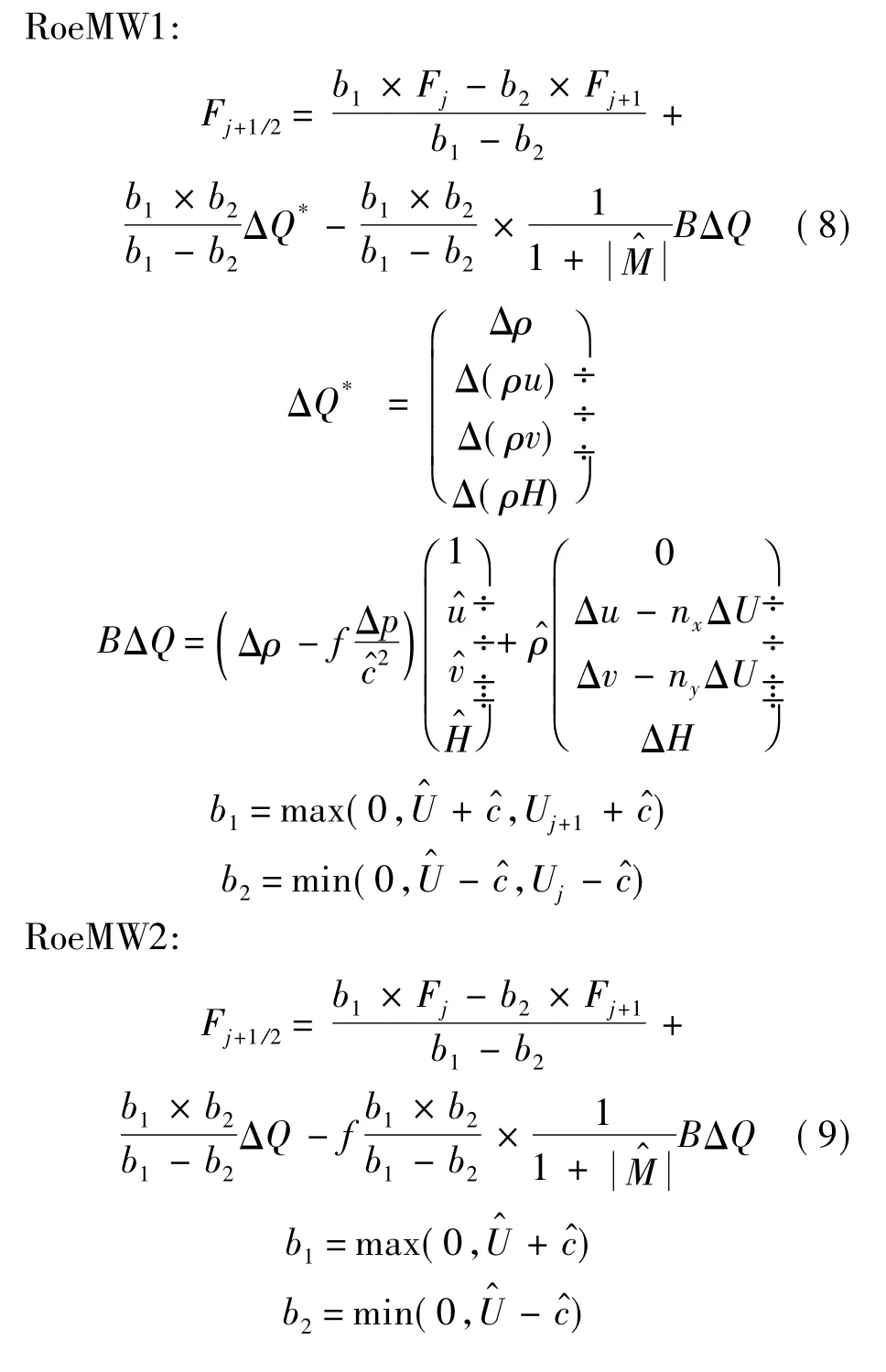
2 算例及结果分析

2.1 一维接触间断问题

本问题的初始条件为

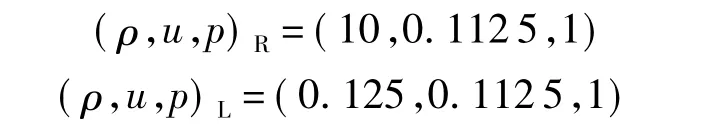
库兰特数(CFL，Courant，Friedrichs，and Lewy)取0.85.为了实现对上述通量格式进行“纯粹”地分析，下文所有的算例结果均由一阶格式计算得到.

从图1～图3可以清晰地看出，3种格式在捕捉到的接触间断基本一致，且速度压强分布曲线无振荡.这表明RoeMW1和RoeMW2格式同Roe格式一样具有较高的黏性分辨率.

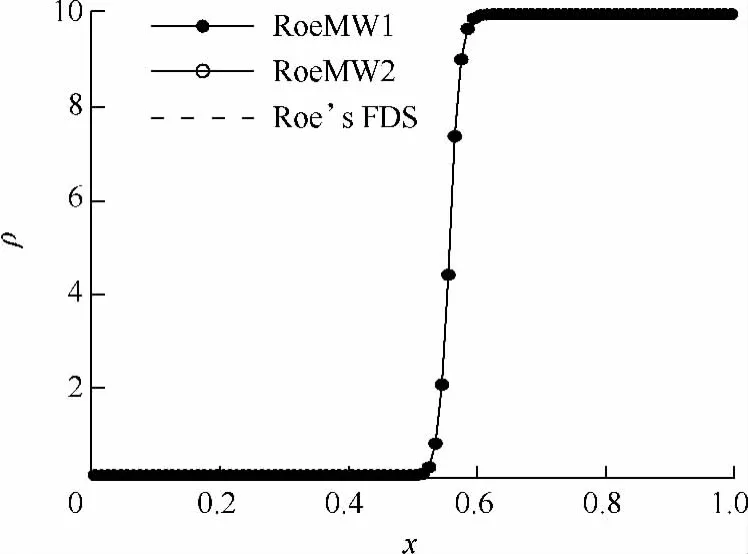
图1 一维接触间断的密度分布曲线

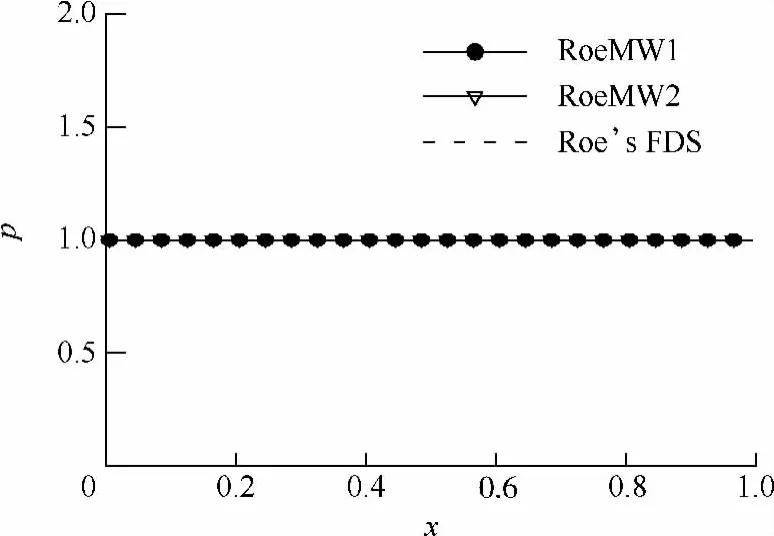
图2 一维接触间断的压强分布曲线

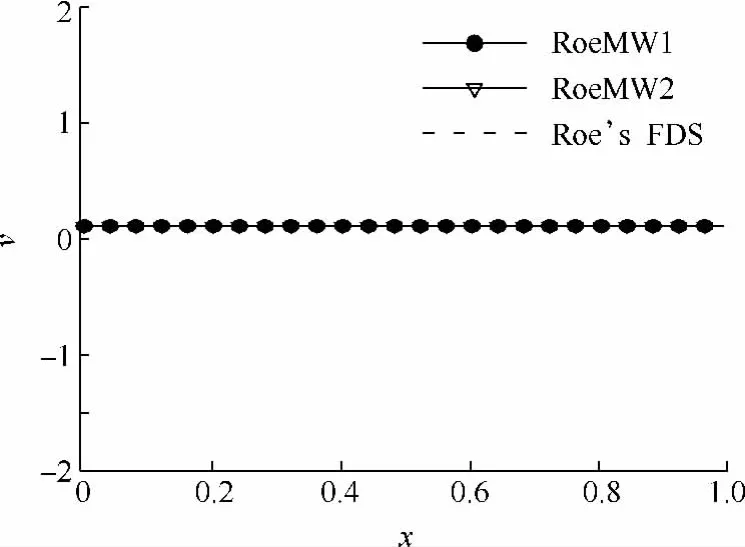
图3 一维接触间断的速度分布曲线

2.2 无黏圆柱超音速绕流

1988年，文献[17]研究发现Roe格式在计算钝头体激波时会产生“粉刺”现象(图4a).而FVS格式则无此现象发生.因此，本算例是判断格式激波稳定性的经典算例.在本文中，取来流马赫数为8，网格量为102×171，CFL数为5.时间格式统一选用无条件稳定的LUSGS方法.

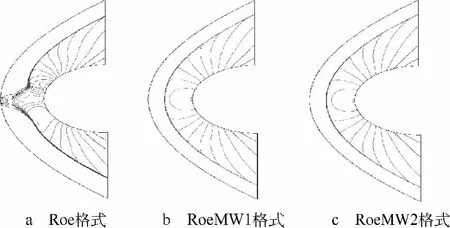
图4 无黏圆柱超音速绕流等压强线图

从图4可以看出，RoeMW1与RoeMW2格式在保证了激波分辨率高的同时均可有效地避免“粉刺”现象的发生.图5则表明RoeMW1与RoeMW2格式在计算该问题时保持总焓守恒.而这一点在预测气动热等气动性能参数时非常重要.

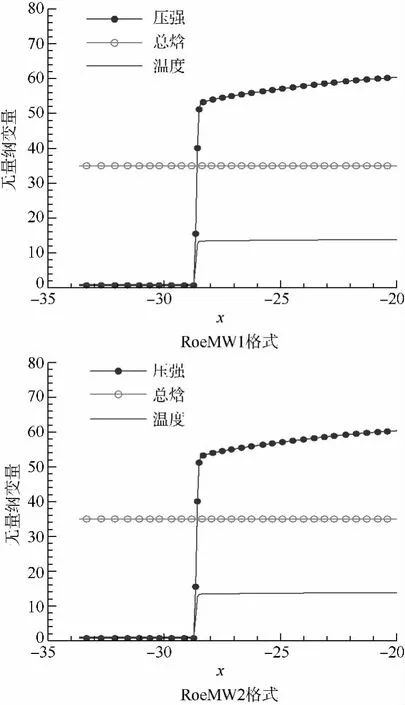
图5 对称线上激波参数显示图

2.3 双马赫反射

该算例最初由Woodward和colella[18]给出，并已成为格式研究的标准算例.其具体描述如下:计算域为[0，4]×[0，1]，其中在下边界[1/6，4]的位置为滑移壁面条件.初始时刻，在计算域中给定一个与x轴成60°夹角的马赫数为10的激波，该激波从x=1/6，y=0的位置一直延伸到上边界，并向右侧快速移动.下边界[0，1/6]的区域以及左边界均给定激波的波后条件，右边界给定出流条件，上边界根据激波每一时刻所处的位置分别给定激波的波前和波后条件.计算时间推进到t=0.2.采用的计算网格为960×240.

图6给出了Roe，RoeM，RoeMW1以及RoeMW2这4种格式计算得到的密度等值线图.从图上可清晰地看到Roe格式在计算正激波时会发生激波不稳定现象.RoeM格式虽然较之于Roe格式有所改进，但依然出现比较明显的激波不稳定现象.相比于RoeM格式，RoeMW1对Roe格式有了更大的改善，但依然无法完全抑制激波不稳定现象的发生.这也与上文所述的仅仅利用函数f来控制压强耗散系数有时并不能完全抑制激波不稳定现象发生的结论一致.同时，从图6中RoeMW2的计算结果可看出，在RoeMW1格式基础上又增加了对密度扰动耗散的RoeMW2格式，则成功地抑制了激波不稳定现象的发生.

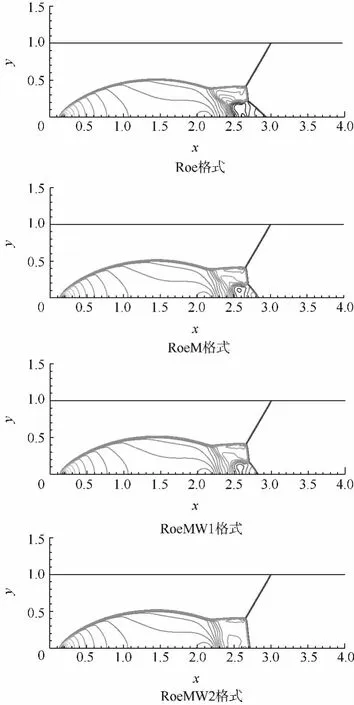
图6 双马赫反射密度等值线图

3 结论

本文通过利用WENO格式中的光滑指示因子来判断流场间断，在RoeM格式的基础上得到了RoeMW1，RoeMW2格式.计算结果表明:一般情况下，构造相对简单的RoeMW1格式在拥有Roe格式黏性分辨率高的优点同时，能够抑制激波不稳定现象的发生并且保证无黏定常计算时的总焓守恒.但在模拟较为复杂的流动结构时，虽然比RoeM格式更加稳定，但RoeMW1格式仅对压强扰动采取控制的方式依然无法完全抑制激波不稳定现象的发生.而同时控制压强扰动与密度扰动的RoeMW2格式则可以在保持RoeMW1格式上述所有优点的基础上解决此问题.因此在实际复杂流动模拟中，它比现有的通量格式(如Roe，RoeM等格式)具有更广阔的应用前景.

References)

[1]Toro E F.Riemann solvers and numerical methods for fluid dynamics[M].Berlin:Springer-Verlag，2009

[2]Jameson A，Schmidt W，Turkel E.Numerical solutions of the Euler equations by finite volume methods using Runge-Kuttta timestepping schemes[R].AIAA 81-1259，1981

[3]Roe P L.Approximate Riemann solvers，parameter vectors and difference schemes[J].J Comp Phys，1981，43:357－372

[4]van Leer B.Flux vector splitting for the Euler equations[J].Lecture Notes in Physics，1982，170:507－512

[5]Liou M S，Steffen Jr C J.A new flux splitting scheme[J].Journal of Computational Physics，1993，107(1):23－39

[6]Liou M S.Progress toward an improved CFD method:AUSM+[R].AIAA 95-1701-CP，1995

[7]Kitamura K，Shima E.Towards shock-stable and accurate hypersonic heating computations:a new pressure flux for AUSM-family schemes[J].Journal of Computational Physics，2013，245:62－83

[8]Liou M S.A further development of the AUSM_scheme，towards robust and accurate solutions for all speeds[R].AIAA 2003-4116，2003

[9]阎超.计算流体力学方法及应用[M].2版.北京:北京航空航天大学出版社，2006

Yan Chao.Computational methods and applications[M].2nd ed.Beijing:Beihang University Press，2006(in Chinese)

[10]Kitamura K，Shima E，Nakamura Y，et al.Evaluation of Euler fluxes for hypersonic heating computations[J].AIAA Journal，2010，48(4):763－776

[11]Kim K H，Kim C，Rho O H.Cures for the shock instability，development of a shock-stable Roe scheme[J].Journal of Computational Physics，2003，185(2):342－374

[12]Jiang G S，Shu C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics，1996，126(1):202－208

[13]Liou M S.Mass flux schemes and connection to shock instability[J].Journal of Computational Physics，2000，160(2):623－648

[14]Kitamura K，Shima E.Improvements of simple low-dissipation AUSM against shock instabilities in consideration of interfacial speed of sound[C]//Proceedings of ECCOMAS CFD.Libson:[s.n.]，2010:14－17

[15]Jameson A.Analysis and design of numerical schemes for gas dynamics，2:artificial diffusion and discrete shock structure[J].International Journal of Computational Fluid Dynamics，1995，5(1/2):1－38

[16]Einfeldt B，Munz C D，Roe P L，et al.On Godunov-type methods near low densities[J].J Comput Phys，1991，92(2):273－295

[17]Peery K M，Imlay S T.Blunt-body flow simulations[R].AIAA88-2904，1988

[18]Woodward P，Colella P.The numerical simulation of two-dimensional fluid flow with strong shocks[J].Journal of Computational Physics，1984，54(1):115－173