基于距离测量的机器人误差标定及参数选定

张 铁 戴孝亮 杜 亮

(华南理工大学 机械与汽车工程学院，广州510640)

由于加工制造和装配，机器人的实际运动学偏离控制器中的名义运动学，导致机器人末端定位精度不足，通常需要建立运动学标定模型，识别实际运动学参数以提高定位精度.机器人运动学标定方法包括轴线测量法[1]和误差模型法[2].轴线测量法是由关节轴线特征辨识实际运动学参数[1];误差模型则是建立了关节参数误差同机器人末端误差的线性解析关系.

对于误差模型法，模型应满足完整性、连续性和最小化[3].模型中存在的冗余参数导致模型奇异，使模型不满足连续性和最小化，降低了参数辨识的有效性.首先需要选用合适的运动学模型.DH模型是最常见的机器人运动学形式，但描述平行关节时存在奇异.为消除DH模型的奇异，国内外提出了很多运动学模型包括:修正DH模型[4－5]、MCPC(Modified Complete and Parametrically Continuous)模型[6]、指数积模型[7]等.

消除模型中冗余参数的方法包括解析法和数值法:①解析法从理论上分析参数的一般关系.文献[8]验证了标定模型的可辨识参数应为4R+2P+6个，其中，R为旋转关节数，P为移动关节数.文献[9]对每个关节设定6个参数，推导出连杆参数误差之间的冗余关系式，指出测量位置而忽略姿态时的可辨识参数降为4R+2P+3个，当末端关节的连杆长度和连杆距离为零时，会进一步减少参数可辨识的个数.②数值法是在特定的模型和关节位形下，处理雅可比矩阵，有QR(Orthogonal－triangular decomposition)分解法[10]、奇异值分解后的正交阵进行初等行变换的方法[11]等，来消除冗余参数.

本文建立了关节连杆参数误差同机器人末端距离平方差的误差模型，分析了模型的冗余参数关系式及其物理解释，确定可辨识参数个数后获得了参数完整的非奇异模型，迭代的最小二乘法用于辨识参数.最后，使用激光跟踪仪，对某公司的6R(旋转关节)工业机器人进行了标定实验.

1 基于距离平方差的标定模型

1.1 机器人运动学

考虑到平行关节轴线的微小偏移引起连杆距离di的极大变化，采用修正DH模型[4]描述机器人运动学.五参数的修正DH模型包括关节角度θi、连杆距离di、连杆长度ai、绕X轴的扭角αi和绕Y轴的扭角βi，相邻两关节的齐次变换矩阵为

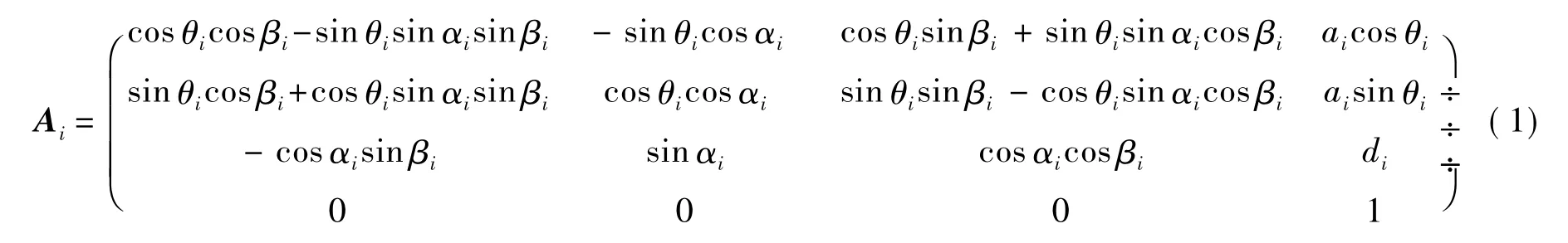
其中，i=0～N，N为机器人自由度;当相邻关节平行或近似平行时，di≡0;当相邻关节不平行时，βi≡0.

当机器人末端法兰盘上安装末端执行器，运动学上需增加工具坐标系{T}，采用六参数{tx，ty，tz，tα，tβ，tγ}描述末端关节坐标系到{T}的变换:

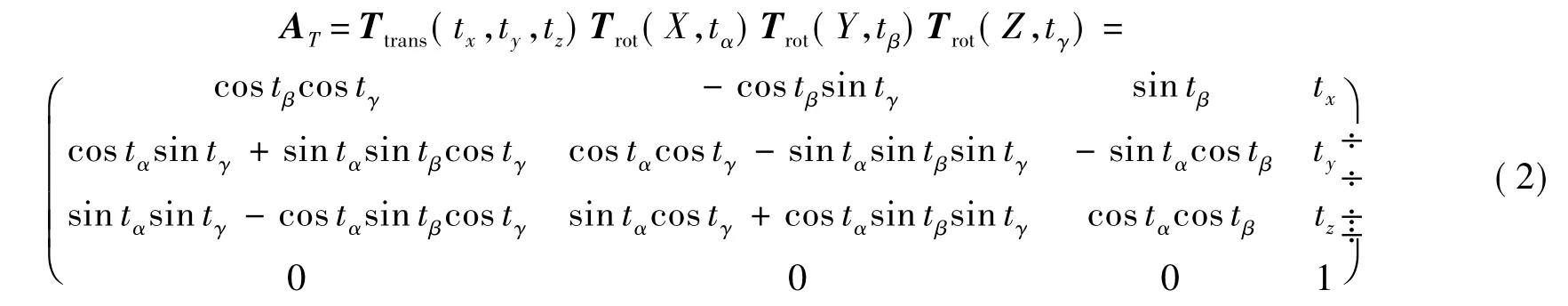
其中tx，ty，tz，tα，tβ和tγ分别表示沿X，Y和Z轴的移动量及绕各轴的旋转量;Ttrans(tx，ty，tz)为沿X，Y，Z轴平移tx，ty，tz对应的齐次变换矩阵;Trot(J，ζ)为绕J轴旋转ζ角对应的齐次变换矩阵(J=X，Y，Z;ζ=α，β，γ).

如图1，对于N自由度的机器人，正运动学为

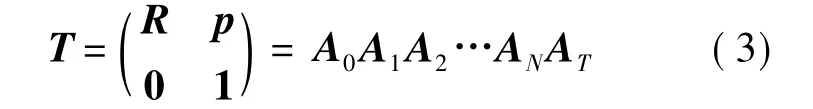
其中，R为位姿T的姿态矩阵;p为位姿T的位置向量;A0为机器人基坐标系{B}相对世界坐标系{W}的齐次变换矩阵，当选取的{W}同{B}重合时，可以去掉A0.

当仅取T的位置部分p，用简化形式表示为

其中，关节角度θ=(θ1，θ2，…，θN)T;关节参数向量η=(γ0，d0，a0，α0，…，γi，di，ai，αi，βi，…，tx，ty，tz，tα，tβ，tγ)T，γi为θi处于零位时的关节角度值;函数f为正运动学位置部分的简化形式.某轨迹第j个位形的位置向量表示为pj=(px，j，py，j，pz，j)T.

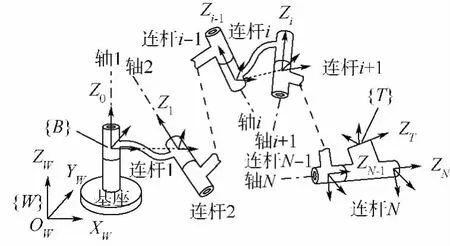
图1 连杆坐标系示意图

1.2 标定模型

式(4)两边对η取一阶导，得到

其中，Δp为机器人末端位置误差向量;Δη为关节参数误差向量;B为相对基坐标系的扩展雅可比.

在任意坐标系中，描述某轨迹第j个位形和第j+1个位形的末端之间距离为

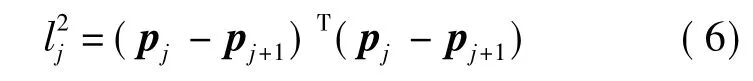
上式两边对p取一阶导，有

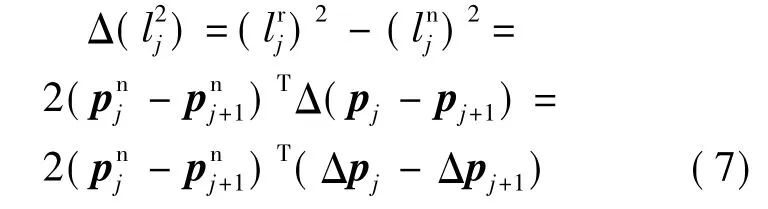
将式(5)代入式(7)，得到

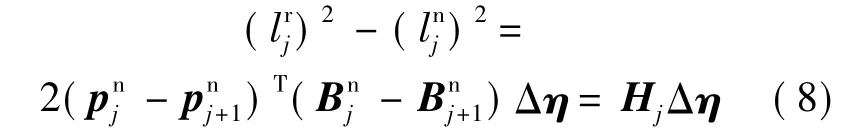
式(8)中，Δη为待辨识的未知量，其余量均可计算得到.当某次测量M个位形的位置，每相邻两点可以得到一个式(8)，共M－1个式子，当M－1大于η参数的个数，联立方程组，得到线性方程组:

其中

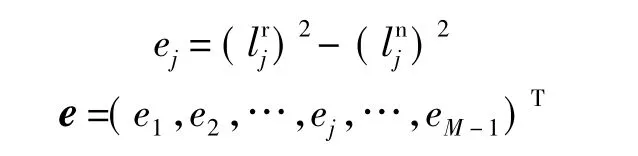
式(9)为辨识方程，反映了关节参数误差到机器人末端距离平方差的误差传递关系.求解式(9)的线性方程组，即可辨识关节参数误差Δη.

2 参数辨识

2.1 冗余参数的消除

为使模型满足完整非奇异，必须对Δη包含的参数进行选取.如图2，可以将Δη中的参数划分为3类:①独立参数，表现为对应H矩阵的列与其他列不相关;②相关参数，表现为对应H矩阵的列成绝对的线性关系;③不起作用参数，即对末端误差无影响，表现为对应H矩阵的列全为零.

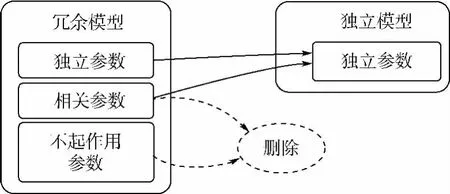
图2 消除冗余参数示意图

冗余参数包含了第3类参数和第2类的部分参数，消除这2类冗余参数如下:①H矩阵的列全为零的情况，该项误差对模型的建模误差无影响，应当直接剔除.②H矩阵的列绝对线性相关的情况，设有I个参数，对应的辨识方程的列有K个线性等式，剔除其中的K个参数，剩余的I－K个参数如果不再含有线性等式，剩余参数独立，为可辨识参数.

对于两参数相关的特殊情况描述如下:假设某两个参数Δηm和Δηn对应辨识方程的列成比例Hm=λHn，其中λ为比例常数.该二项误差对机器人末端误差联合作用效果为HmΔηm+HnΔηn=λHnΔηm+HnΔηn=Hn(λΔηm+Δηn)，可以令Δη*n=λΔηm+Δηn.实际上，模型只能辨识参数Δη*n，而无法辨识单独的参数Δηm或Δηn.将辨识得到的参数Δη*n赋给Δηn，而忽略Δηm.该做法等价于将Δηm和对应的列Hm删除.

2.2 距离平方差模型的可辨识参数

参照文献[12]，Bd1和 Bγ1的求解如下式:

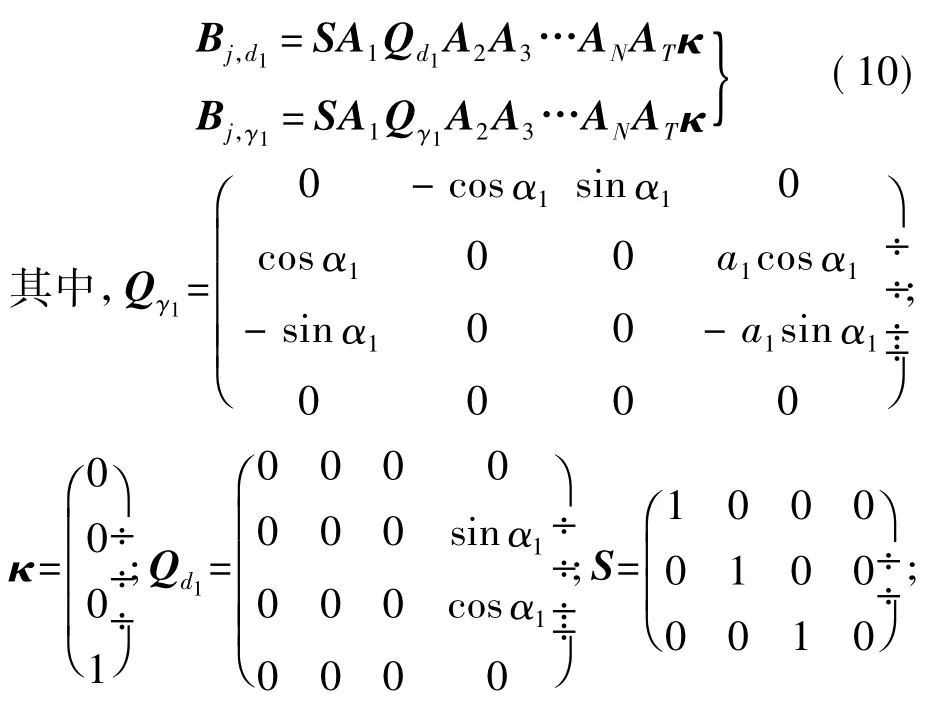
左乘S和右乘κ代表提取矩阵第4列的前3个数.按照式(10)，使用字符运算方法，总存在下式:

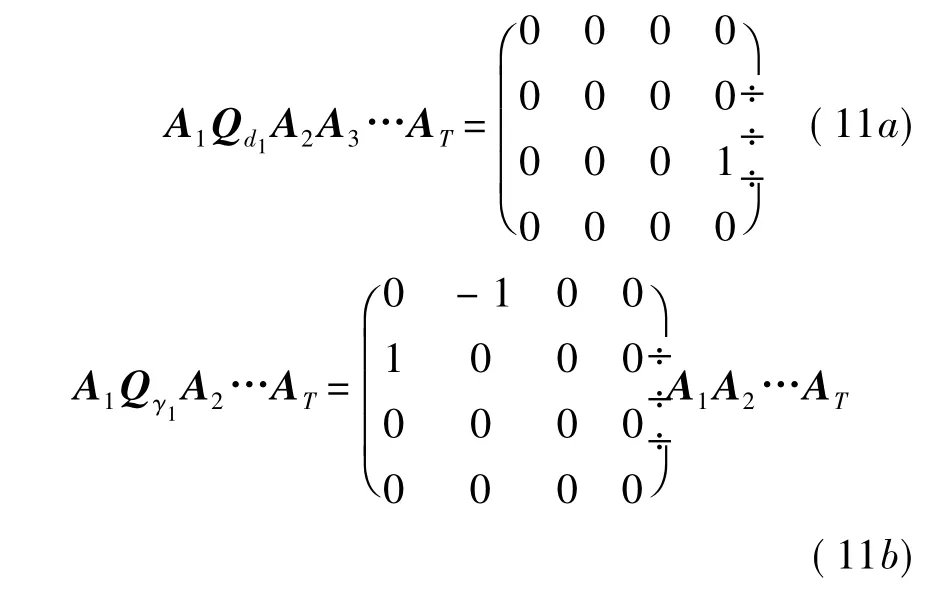
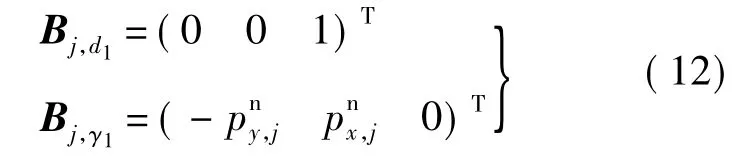
将上式代入式(8)，得到Δd1和Δγ1对应Hj向量中的两元素 Hj，d1和 Hj，γ1为 0 ，故总存在

式(13)显示，Δd1和Δγ1对末端距离平方差没有贡献，为冗余参数，应当从标定模型中剔除.如图3，参数d1和γ1同基坐标系的选取有关.相对于位置测量模型，距离测量模型省去了测量坐标系{C}到{B}的变换[13]，模型中不需要A0，Δd1和Δγ1.

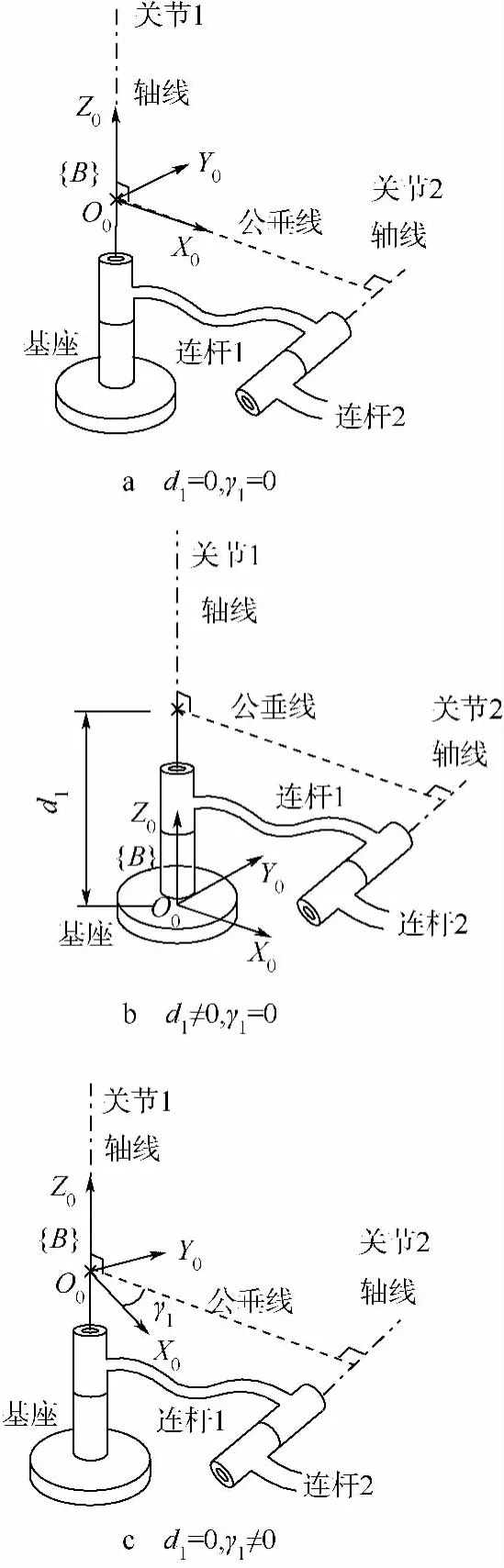
图3 基坐标系的选定影响参数d1和γ1值

相邻关节轴线平行时的情况如图4所示.对于关节i和关节i+1平行时，同一结构的连杆关节，di和di+1对连杆坐标系的影响是一致的，两参数相关，如式(14).其中一个参数多余，可剔除di，保留di+1.这就是文献[4]中平行关节引入参数βi时，应去掉di.

文献[9]指出当aN=0(运动学模型与本文有区别，等价于本文aN=tx=ty=0且αN=0情况)且末关节为旋转关节时，模型将减少2个可辨识参数.故在设计末端执行器时，测量点应偏离末端关节轴线，否则将存在下式:

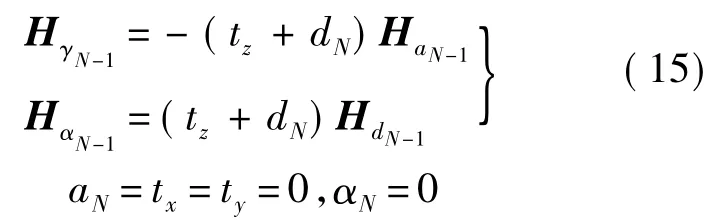
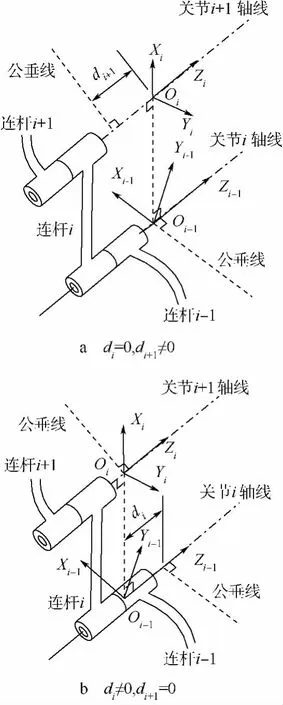
图4 平行关节参数di和di+1的相关性

对于工具坐标系参数，AT六参数和AN四参数相关，需剔除AN参数.对于位置测量和距离测量模型，AT中只能辨识3个位置参数tx，ty和tz.按照式(13)～式(14)的冗余关系式，将冗余参数剔除，得到非奇异的模型，模型可辨识参数见表1.

表1 距离测量模型的可辨识参数

2.3 辨 识

采用迭代的最小二乘法[7]求解式(9)的线性方程组:

当H的秩rank(H)等于Δη的参数个数时，HTH非奇异，是式(16)计算的前提.当Δη＜ε时，停止迭代并输出结果，其中，ε为一个很小的数，如10－5.用Δη＜ε作为终止条件，判断辨识过程是否趋于稳定.

3 测量与补偿实验

使用激光跟踪仪，应用距离平方差的标定模型，对某公司的6R工业机器人进行标定见图5.

图5 实验现场

所使用的激光跟踪仪测量系统为德国莱卡公司的Leica AT901－B，对于2.5 m×5 m×10 m空间的测量精度为±10 μm+5 μm/m.该测量系统包括绝对跟踪仪、控制器、安装有Polyworks V11软件的应用计算机、反射球和球座.

末端执行器安装于机器人末端法兰盘上，末端执行器上的强磁铁将球座吸引，反射球置于球座上，被球座上的强磁铁吸引.在设计末端执行器结构时，反射球的球心点作为目标测量点，应偏离末关节轴线一定距离，以保证A5参数的可辨识.

对于6R机器人，可辨识参数的个数应为4R－3=21个，包括18个机器人本体参数和3个工具参数.冗余参数包括:对末端误差无贡献，或者可将对末端贡献的误差转移到可辨识参数上.故令模型中所有冗余参数值为零，包括γ1，d1，d2，γ6，d6，a6，α6，tα，tβ，tγ.如图6所示.连杆坐标系存在以下关系:①由于γ6，d6，a6和α6为零，当θ6为零时，连杆5固连的坐标系O5X5Y5Z5与连杆6固连的坐标系O6X6Y6Z6绝对重合;②tα，tβ，tγ为零，坐标系O6X6Y6Z6与工具坐标系{T}平行.

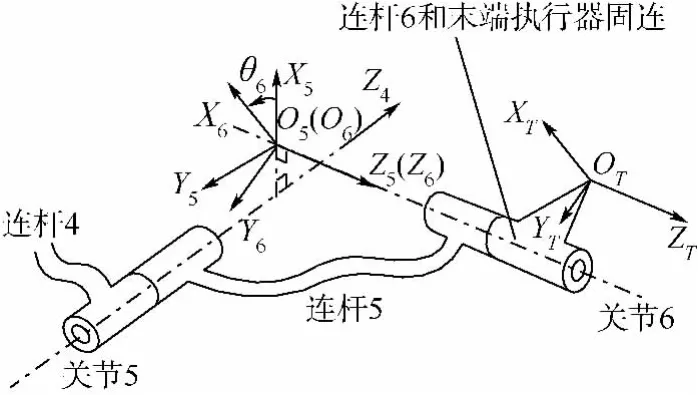
图6 末端坐标系示意图

工具参数的初值需要事先测定.①单独旋转关节5而令其余关节处于零位，末端测量点形成一圆轨迹，根据圆轨迹获得关节5的轴线;同理，获得关节6的轴线.提取关节5和关节6的公垂线，以关节6轴线为Z5轴，公垂线为X5轴，关节6轴线与公垂线的交点为原点O5，建立坐标系O5X5Y5Z5.②当θ6为零时，O5X5Y5Z5与O6X6Y6Z6重合，此时以O5X5Y5Z5为参考坐标系，将目标测量点的三维坐标作为(tx，ty，tz)的初值.该过程可以在软件Polyworks中完成.

示教机器人位形，编制机器人运动程序:示教点尽量充满整个工作空间，且末端反射球朝向激光跟踪仪;保存示教数据后，编制机器人运动程序，机器人每运动到一个位形，机器人暂停3 s，激光跟踪仪自动触发采集反射球中心的三维坐标值;将位形的测量坐标数据和控制器中示教关节数据分别通过USB接口输出.

实验共采集了2批数据:第1批包含70组位形的数据，用于辨识运动学参数;第2批包含32组位形的数据，用于检验新运动学参数对精度的改善.测量数据的空间位置分布如图7所示.

图7 测量点的空间位置分布图

如图8所示，由70组位形数据计算运动学参数，经过1次迭代，32组检验位形的距离误差均方根由3.172 mm下降到0.220 mm，经过第2～3次迭代，距离误差有微量的减少，说明:迭代已趋于稳定，且实际模型的线性度很高.经过3次迭代，辨识得到的新运动学参数如表2～表3所示，校正前后32组检验点距离误差对比如图9所示，表4显示检验点距离误差的均方根减少了93.1%，机器人的定位精度得到显著提高.

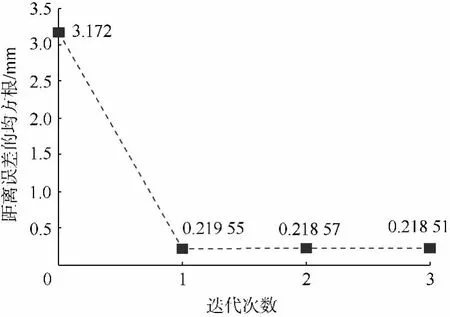
图8 检验点距离误差均方根随迭代次数的变化

表2 工具参数标定前后值 mm

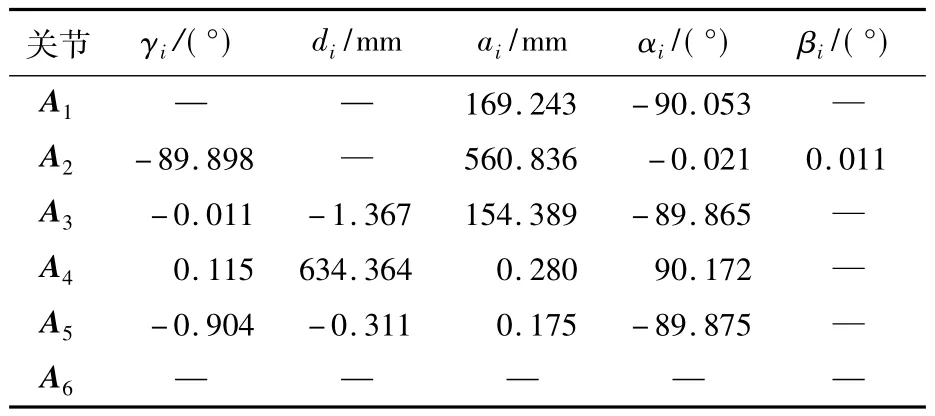
表3 辨识得到的运动学参数

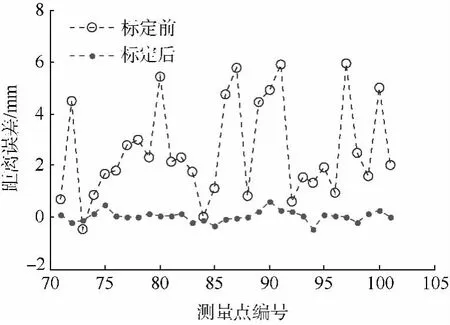
图9 检验点校正前后误差对比图

表4 检验点距离误差统计量 mm

4 结论

1)使用相对基坐标系的雅可比矩阵，建立关节参数误差到机器人末端距离平方差的标定模型，为距离测量的一种形式，不需要测量坐标系到机器人基坐标系的转换，简化了测量过程.

2)从冗余关系式和物理解释的角度，分析了距离平方差模型的冗余参数，确定可辨识参数，获得参数完整的非奇异模型，提高了辨识可靠性，为距离测量模型的参数选定提供了依据.

3)实验中，为保证倒数第2关节参数的可辨识，设计末端执行器时，测量点应偏离末端关节的轴线一定距离.实验结果显示机器人误差减少了93.1%.

References)

[1]Santolaria J，Ginés M.Uncertainty estimation in robot kinematic calibration[J].Robotics and Computer－Integrated Manufacturing，2013，29(2):370－384

[2]Lightcap C，Hamner S，Schmitz T，et al.Improved positioning accuracy of the PA10－6CE robot with geometric and flexibility calibration[J].IEEE Transactions on Robotics，2008，24(2):452－456

[3]Schröer K，Albright S L，Grethlein M.Complete，minimal and model－continuous kinematic models for robot calibration[J].Robotics and Computer－Integrated Manufacturing，1997，13(1):73－85

[4]Hayati S A.Robot arm geometric link parameter estimation[C]//Proceedings of the 22nd IEEE Conference on Decision and Control.Piscataway，NJ:IEEE，1983:1477－1483

[5]丁希仑，周乐来，周军.机器人的空间位姿误差分析方法[J].北京航空航天大学学报，2009，35(2):241－245

Ding Xilun，Zhou Lelai，Zhou Jun.Pose error analysis of robot in three dimension[J].Journal of Beijing University of Aeronautics and Astronautics，2009，35(2):241－245(in Chinese)

[6]陈钢，贾庆轩，李彤，等.基于误差模型的机器人运动学参数标定方法与实验[J].机器人，2012，34(6):680－688

Chen Gang，Jia Qingxuan，Li Tong，et al.Calibration method and experiments of robot kinematics parameters based on error model[J].Robot，2012，34(6):680－688(in Chinese)

[7]He R B，Zhao Y J，Yang S N，et al.Kinematic－parameter identification for serial－robot calibration based on POE formula[J].IEEE Transactions on Robotics，2010，26(3):411－423

[8]Everett L J，Suryohadiprojo A H.A study of kinematic models for forward calibration of manipulators[C]//Proceedings of the 1988 IEEE International Conference on Robotics and Automation.Piscataway，NJ:IEEE，1988，2:798－800

[9]Meggiolaro M A，Dubowsky S.An analytical method to eliminate the redundant parameters in robot calibration[C]//Proceedings of the 2000 IEEE International Conference on Robotics and Automation.Piscataway，NJ:IEEE，2000:3609－3615

[10]Khalil W，Besnard S，Lemoine P.Comparison study of the geometric parameter calibration methods[J].International Journal of Robotics and Automation，2000，15(2):56－67

[11]王品，廖启征，庄育锋，等.一般7R串联机器人标定的仿真与实验[J].机器人，2006，28(5):483－487，494

Wang Pin，Liao Qizheng，Zhuang Yufeng，et al.Simulation and experimentation for calibration of general 7R serial robots[J].Robot，2006，28(5):483－487，494(in Chinese)

[12]张铁，戴孝亮.基于距离误差的机器人运动学标定[J].华南理工大学学报:自然科学版，2011，39(11):98－103

Zhang Tie，Dai Xiaoliang.Kinematic calibration of robot based on distance error[J].Journal of South China University of Technology:Natural Science Edition，2011，39(11):98－103(in Chinese)

[13]谭月胜，孙汉旭，贾庆轩，等.基于旋量理论及距离误差的机械臂标定新方法[J].北京航空航天大学学报，2006，32(9):1104－1108

Tan Yuesheng，Sun Hanxu，Jia Qingxuan，et al.New manipulator calibration method based on screw theory and distance error[J].Journal of Beijing University of Aeronautics and Astronautics，2006，32(9):1104－1108(in Chinese)