二自由度超声波电动机力矩测试方法研究

胡锡幸，马 青，褚明华，王 剑，郭吉丰

(1.国网浙江省电力公司杭州供电公司，杭州 310009;2.浙江省火电建设公司，杭州 310016;3.国网嘉兴供电公司，嘉兴 314005;4.浙江大学，杭州 310027)

0 引 言

多自由度球形超声波电动机是近年来超声波电动机领域的研究热点［1］。其中，电机的力矩检测一直是研究的难点，原因在于电机球形转子输出的是多维运动，单自由度电机的测试方法不能简单地复制，需要提出新的测试机构和方法。

目前，国内外关于多自由度球形超声波电动机的性能检测机构研究比较少。文献［2］给出了电机绕各轴的最高转速，但未给出电机堵转力矩的数值。文献［3－5］给出了多自由度球形超声波电动机的空载转速和堵转力矩，但对电机的检测机构未加说明。多自由度超声波电动机的输出力矩值较小，且方向又是多自由度的，导致电机的力矩检测困难。多自由度电机性能测量中往往把多个方向解耦，然后逐一测量各方向的转速和力矩。力矩的计算方法是用输出轴拉动滑轮牵引的物体，物体的质量与滑轮的半径之积即是电机的力矩［6－8］。但利用该方法测量多自由度超声波电动机的力矩存在缺陷，当输出轴跟随球转子运动时，滑轮的有效直径会发生变化，得到的力矩值也会产生误差;检测完电机某一自由度的性能后，需要重新安装测试机构，测试过程比较繁复。

因此研究适合多自由度球形超声波电动机的力矩检测机构，实现高精度的电机控制是当前球形电机应用中亟需解决的关键问题。本文以实验室自主研制的基于三定子的二自由度球形超声波电动机为研究对象，提出了一种新型的基于压力传感器的电机力矩检测机构。文中首先介绍电机的力矩测试机构的结构形式;其次阐述测试的原理和方法;最后，对电机力矩进行实测，验证该方案的有效性和精确度。

1 力矩测试机构

1.1 结构形式

基于三定子的二自由度球形超声波电动机力矩测试机构的结构如图1所示，这些零件组成了力矩测试模块。测试机构上下对称。

力矩测试模块的元件与装配过程如图2所示。其中，上座沿周向开槽四个，将压力传感器固定在槽内，传感器的触头方向均指向圆心。下座采用四个方柱，通过沉头螺钉配合上座，用来固定压力传感器。测力杆的中部有环形凸台，底部设有安装硬木凹压头的孔，孔与硬木凹压头采用过盈配合。固定盖帽和固定板之间有螺纹固定，避免底部力矩测试模块因自身重力与球转子脱开。

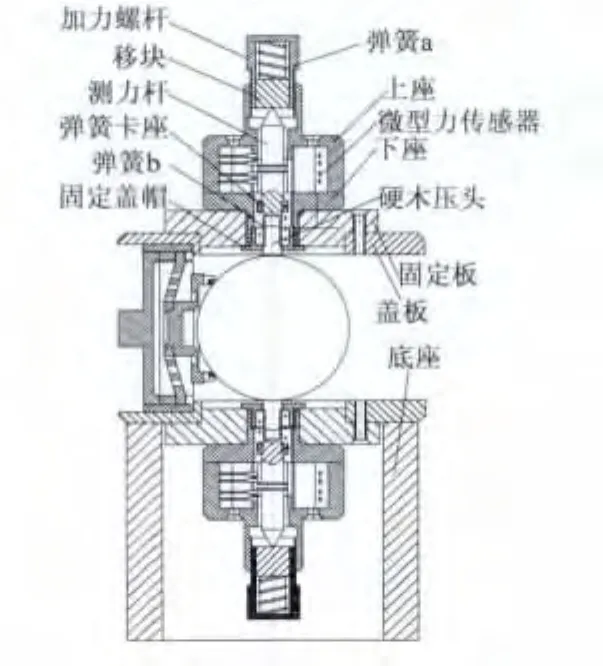
图1 力矩测试机构结构图

图2 力矩测试模块装配图

在力矩测试机构设计中有几处需要特别说明:弹簧a的使用是为了减小加力螺杆8的加力刚度。弹簧b的刚度系数需要合理设计，不能太小也不能过大。如果刚度系数太小，会导致即使加力螺杆拧紧到底时，硬木压头和球转子之间的压力不够大，从而测不出电机的堵转力矩;刚度系数太大，会出现加力螺杆稍微一拧紧，电机就“堵死”的情况。同样，压头和球转子的摩擦系数需合理选择设计，不能太小也不能过大:太小容易打滑，过大也会将球转子“堵死”。这里选择用硬木材料，它和球转子的摩擦因数为0.3左右。弹簧b在这套机构里的目的是确保加力螺杆往回拧时，硬木压头也会随之反弹而脱离球转子，方便调试。加力移块的中心处有一个内锥型的小凹点，是为了和测力杆顶部锥形顶点配合。这样设计的目的是为了使测力杆有微小的活动余量，使其既能与压力传感器的触头接触，又不会“跑偏”。

1.2 工作原理

力矩测试机构的工作原理:当同时拧紧球转子顶部和底部上的加力螺杆，移块因为弹簧对它的作用也随之下降或上升，这时顶部和底部的硬木压头就压住球转子，球转子被两端的硬木压头紧紧地“顶住”。当电机处于工作状态时，硬木压头与球转子之间发生相对运动，两者的摩擦力使测力杆产生微量偏移，其中若干个压力传感器的触头便与测力杆中间的环形凸台相接触，压力传感器即产生读数。硬木压头与球转子之间的摩擦力可根据力矩平衡的原理换算得到，在球转子的半径和硬木压头个数给定情况下，便可求得电机的输出力矩。

2 测试方法

设顶部和底部的硬木压头对球转子的正压力均为Fn，当硬木压头与球转子之间发生相对运动(运动趋势)的情况下，两者就会产生摩擦力(静摩擦力)。假定球转子的半径为r，顶部和底部的硬木压头和球转子之间的摩擦力分别为fr1和fr2，如图3所示。fr1和fr2是一对力偶，它们对球心的力偶矩TL:

式中:μ是球转子和硬木压头之间的摩擦因数。

根据力矩平衡原理，如图4所示，可得到凸台与压力传感器的触头之间的压力fr与fr1有以下关系:

图3 球转子的力矩示意图

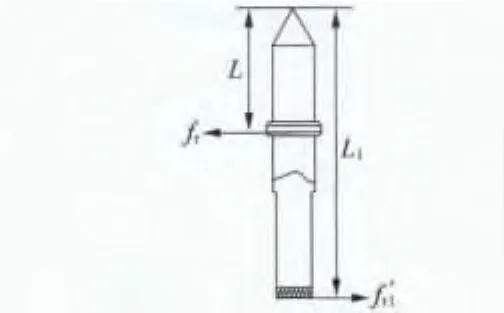
图4 测力杆力矩平衡示意图

凸台与压力传感器的触头之间的压力fr与力传感器输出的电信号值Ub满足线性对应关系，即:

式中:k为力传感器的输出电压信号与所受压力的比例系数。

所以，TL可表示:

根据球转子的动力学方程，有:

式中:TM为电机输出力矩;ωR为球转子的角速度;J为球转子的转动惯量。当ωR≠0时，μ取动摩擦因数;当ωR=0时，μ取静摩擦因数。

当球转子的角速度ωR趋于稳定时，则有:

所以电机的输出力矩TM可根据力传感器输出的电信号值Ub得到。

3 实验测试

3.1 测试电路

力传感器采用Honeywell的FSG15N1A触力型压力传感器，DIP超小封装，直径为5 mm的按钮作为触头，额定负载为1500 g，有5 kg的过载能力。最小分辨率1 g，线性度和重复性好，精度完全符合力矩测试机构的要求。

压力传感器FSG15N1A的工作电压为10 V，在额定负载为1500 g下输出360 mV的电压信号，使用时需要把毫伏级的电压信号放大到伏级。采用两级放大电路，如图5所示。第一级选择高精度运放AD620作为小信号的放大，第二级由运放OP07完成信号的低通滤波和二次放大。

图5 信号放大滤波电路

3.2 测试结果

力矩测试机构在实际测量时需注意以下两点:

(1)在拧紧球转子顶部和底部的两个加力螺杆时，需保证两者的螺纹进给量一致，使两端压头和球转子之间的压力值一样，保证两端压头对球转子的摩擦力(矩)一致。

(2)在拧紧加力螺杆前后，确保测力杆的环形凸台和压力传感器的触头不接触，压力传感器的输出为零。设计时它们之间的缝隙距离为0.5 mm，如电机运行前压力传感器就有输出值，说明在加载时测力杆倾斜，环形凸台已接触压力传感器的触头，需重新加载预紧力。

首先确定力传感器输出电压值与所受压力值之间的对应关系，通过调节放大电路的放大倍数b进行标定。这里取k=1，标定后力传感器的输出电压值Ubs和经放大电路输出的电压值与所受压力值Fns之间的关系如图6所示，标定后Fns=

电机结构参数:L1=40 mm，L2=16 mm，r=20 mm。保持电压峰峰值Vpp=350 V，在x轴和y轴两个方向测得的电机堵转力矩随预紧力Fc变化规律如图7所示;保持Fc=30 N，在x轴和y轴两个方向测得的电机堵转力矩随电压峰峰值Vpp变化规律如图8所示。从图中可见，随着预紧力和驱动电压的增大，电机的堵转力矩也相应增加。

图6 力传感器输出电压与正压力Fns的关系图

图7 电机堵转力矩随预紧力的变化曲线

图8 电机堵转力矩随电压峰峰值的变化曲线

4 结 语

本文提出了一种新型的基于压力传感器的二自由度球形超声波电动机的力矩测试机构，并根据力矩平衡原理阐述了测试原理和方法。实验证明该测试机构能满足二自由度球形超声波电动机力矩的测试要求，具有精度高、结构巧妙和体积紧凑等特点。

［1］郭吉丰，白洋，王剑.多自由度超声波电机的研究进展和展望［J］.振动与冲击，2013，32(15):1 －7.

［2］金龙，胡敏强，顾菊萍，等.一种新型圆柱定子3自由度球形压电超声电机［J］.东南大学学报(自然科学版)，2002，32(4):620－623.

［3］赵学涛.夹心换能器式多自由度球形超声波电动机研制［J］.微特电机，2009，37(4):7 －10.

［4］傅平，沈润杰，帅光举，等.二自由度行波型超声波电机的研制［J］.宇航学报，2009，30(1):367 －372.

［5］徐志科，金龙，胡敏强，等.一种新型双定子三自由度超声波电机特性研究［J］.微电机，2009，42(4):27 －29.

［6］赵淳生.超声电机技术与应用［M］.北京:科学出版社，2007:267－270.

［7］TAKEMURA K，MAENO T.Design and control of an ultrasonic motor capable of generating multi－ DOF motion［J］.IEEE/ASME Transactions on Mechatronics，2001，6(4):499 －506.

［8］MASHIMO T，TOYAMA S，ISHIDA H.Design and implementation of spherical ultrasonic motor［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2009，56(11):2514 －2521.