一种简易的无刷直流电动机直接转矩控制

周 衍，张兴华

(南京工业大学，南京 211816)

0 引 言

无刷直流电动机因其效率较高、控制简单、运行平稳，在白色家电、电动车等领域得到了广泛的应用，但是电磁转矩脉动问题制约了其在高精度高稳定性场合的应用。

80 年代中期，Takahashi［1］和 Depenbrock［2］最先提出了对感应电机采取直接转矩控制。90年代末，直接转矩控制被用于面贴式和内置式的永磁同步电机控制系统之中［3］。为了更有效地降低转矩脉动，无刷直流电动机的直接转矩控制逐渐被越来越多的学者重视［4］。文献［4］通过分析，计算出了两相导通模式静止坐标系下的无刷直流电动机控制系统转矩表达式，通过加入微分调节观测磁链，降低转矩脉动，但是计算方法较复杂。文献［5］舍去磁链估算环节，对最优的电压矢量进行选择实现无刷直流电动机的直接转矩控制，达到抑制转矩脉动的目的。传统的直接转矩控制方法通过对转矩和磁链计算，然后选择适合的电压矢量调节，可以实现电机转矩的控制［6］，但大多采用6分区的电压矢量空间。由于分区较宽，会导致转矩不够平稳，未能完全发挥直接转矩控制的优良性能［7］。所以，为了使得磁链更平滑、转矩脉动更小，增加扇区和电压矢量的数量就变得非常有意义。

文献［8］实现了一种三三导通的无刷直流电动机控制系统，相比于传统的二二导通模式，该模式在高速运行状态有效缩短了换相时间，减小转矩脉动。二二导通和三三导通的模式均为6个电压矢量的控制系统，将电周期分为6个60°扇区。文献［9］将这两种导通模式相融合，提出了一种新的混合二三导通模式的直接转矩控制，通过仿真验证其新型理论的有效性。

本文详细讨论无刷直流电动机二二导通模式和三三导通模式，并结合两种导通模式的电压矢量，得到新的12扇区划分的直接转矩控制系统，即一种新的二三导通模式。通过理论分析，选择合适的电压矢量，实现此二三导通模式的控制方法，该控制系统简单，易于实现。

1 二二导通模式

二二导通模式无刷直流电动机控制系统中，如果忽略换相过程，任意时刻均是两相导通一相关断。一个周期内，二二导通模式的上下桥臂3对功率管构成控制逆变器的共6种组合。6个功率管组合分别是 V1( 100001)、V2( 001001)、V3( 011000)、V4( 010010)、V5( 000110)、V6( 100100)，六个数字依次表示功率管T1至T6导通关断状态，1表示导通，0表示关断(下同)。6个功率管组合将一个电周期360°分为6 个60°区间。

传统的二二导通模式，分别在 30°、90°、150°、210°、270°、330°这六个换相点换相，换相点所施加的电压矢量依次是 V6( 100100)、V1( 100001)、V2( 001001)、V3( 011000)、V4( 010010)、V5( 000110)，a相电流和反电动势如图1所示，相电流在理想情况下导通120°。

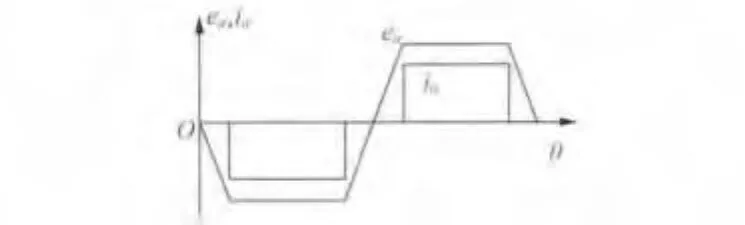
图1 二二导通模式的a相电流和反电动势

如果基于直接转矩控制的思想来施加电压矢量的话，6个电压矢量将空间划分为6个扇区I到VI。如图2所示(箭头表示电压矢量，实线为扇区划分，30°、90°、150°、210°、270°和 330°分别为霍尔边缘检测位置，下同)。

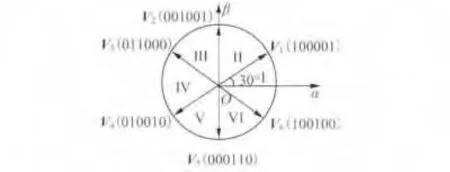
图2 αβ坐标轴下二二导通模式下的电压矢量

根据无刷直流电动机无磁链观测的直接转矩控制相关理论，当转子位于扇区I时，V2和V5在不改变磁链的情况下，增大和减小转矩［7］。在扇区I内，V3减小磁链，增大转矩;V4减小磁链，增大转矩;V1增大转矩和磁链;V6增大磁链，减小转矩。通过以上简单的分析，可以得到二二导通模式下的直接转矩控制开关表，如表1所示，Ψ和τ分别表示磁链和转矩的调节信号，其中1表示该量需增加，-1表示减小，0表示不变(下同)。

表1 二二导通模式下电压矢量开关表

2 三三导通模式

三三导通模式为三相任意时刻全导通，不同于二二导通的通两相断一相的形式，每个功率管导通180°。理想的相电流和反电动势如图3所示，三三导通对应的换向点分别是固定坐标轴α轴的0°、60°、120°、180°、240°、300°和 360°，对应的施加的电压矢量分别是 V6( 100110)、V1( 100101)、V2( 101001)、V3( 011001)、V4( 011010)、V5( 010110)。

图3 三三导通模式的a相电流和反电动势

与之前分析二二导通的类似，再按直接转矩控制的思想，对三三导通模式进行分析。6个电压矢量将坐标轴αβ划分为6个扇区，将每个电压矢量30°角度内作为一个扇区，如图4所示。

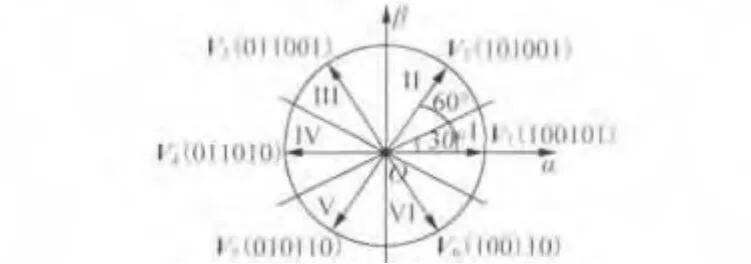
图4 αβ坐标轴下三三导通模式的电压矢量

推导三三导通模式电压矢量开关表的方法与二二导通模式的方法类似。但有所区别，比如当转子在扇区I内(不考虑扇区边缘的临界时刻)，任意一个电压矢量中都无法在不改变定子磁链的情况下，调节转矩，所以三三导通的开关表与二二导通的开关有所区别，没有Ψ=0一栏，如表2所示。

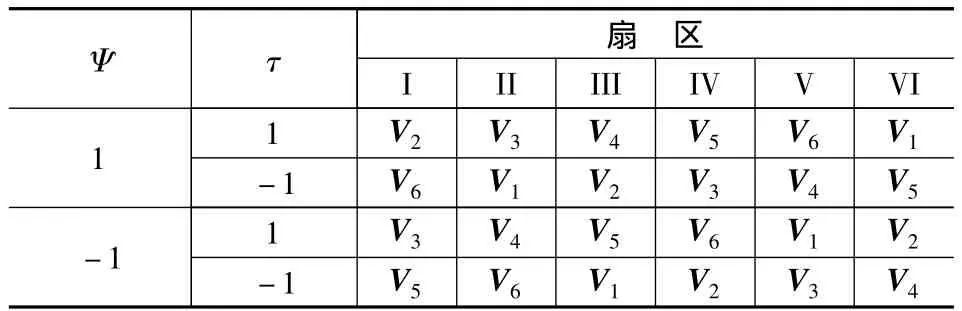
表2 三三导通模式下的电压矢量开关表

3 二三导通模式

为了更有效地减小转矩脉动，通过比较图2和图4，将二二导通模式和三三导通模式相结合，得到新的二三导通模式，该导通模式共有12个电压矢量，如图5所示，电压矢量增加使60°扇区变为30°扇区，相比6电压空间矢量的控制方法，12个电压矢量的调节在控制定子磁链和转矩更准确。二三导通的电压矢量依次是V6( 011010)、V1( 100001)、V2( 101001)、V3( 001001)、V4( 011001)、V5( 011000)、V7( 010010)、V8( 010110)、V9( 000110)、V10( 100110)、V11( 100100)、V12( 100101)，αβ 坐标轴下的电压矢量如图5所示。

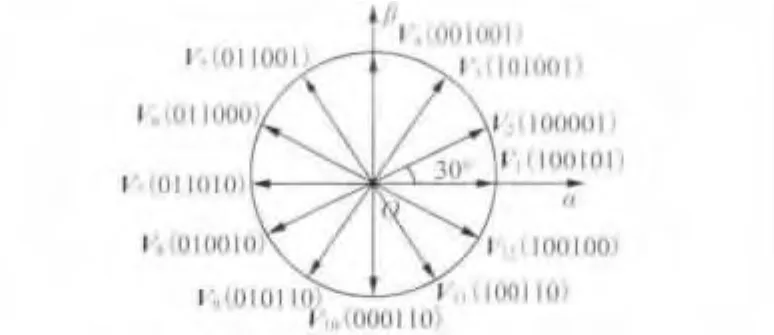
图5 αβ坐标轴下的二三导通模式电压矢量

12个电压矢量组合分成12个扇区，扇区划分如图6所示。二三导通划分扇区的方法和三三导通一样，二三导通是电压矢量的15°范围内作为一个扇区。

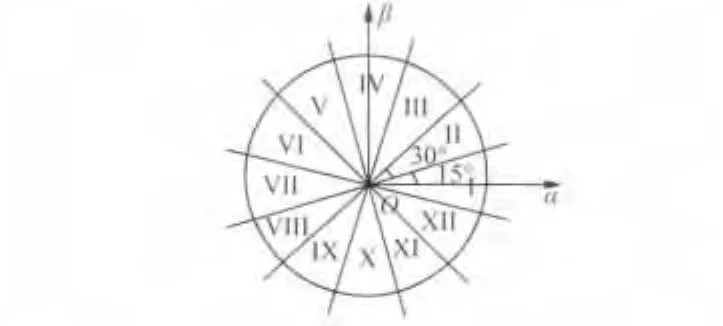
图6 αβ坐标轴下的二三导通模式扇区

遵循前面分析二二导通和三三导通直接转矩控制的方式，当转子位于扇区I时，V2和V3分别在不同程度地增加磁链和转矩;V11和V12分别增加磁链，减小转矩;V5和V6分别减小磁链，增加转矩;V8和V9减小磁链和转矩;可以近似地认为V4和V10在不改变磁链的情况下，增加和减小转矩。

由上述分析，可以得到二三导通模式下的电压矢量开关表，如表3所示［9］。

表3 二三导通模式下的电压矢量开关表

文献［5］对无磁链观测的无刷直流电动机直接转矩控制进行了详细的分析，得到转矩偏差ΔT的表达式:

式中:p为极对数，Δφsq为定子交轴磁链变化量，Lq为电机交轴电感，φr为转子磁链，θe为转子相对于α轴夹角。

由于机械时间常数远大于电气时间常数，在电压矢量作用的时间内，认为转子基本保持不变。转子位置不变的情况下也保持不变，根据式(1)，为迅速调节转矩偏差，应该选择交轴分量最大的电压矢量。

在选择电压矢量时候，在表3中只选择Ψ=0情况下的开关表对转子控制，即近似地在保持定子磁链幅值不变的情况下，施加垂直于转子磁链方向的电压矢量，迅速补偿转矩偏差，以扇区I为例，如图7所示。

图7 扇区I中转子磁链与电压矢量

图中Ψr为转子磁链，选择施加的电压矢量近似地认为与30°扇区垂直，转子在扇区I内，当需要增加转矩时，施加V4，反之则增加V10，随着转子转动到不同的扇区，以此规律，得到表4。

表4 电压矢量选择表

4 实验结果

本文以TI公司DSP芯片TMS320F2812为控制核心，以一台永磁无刷直流电动机和驱动模块搭建实验平台，实验框图如图8所示。

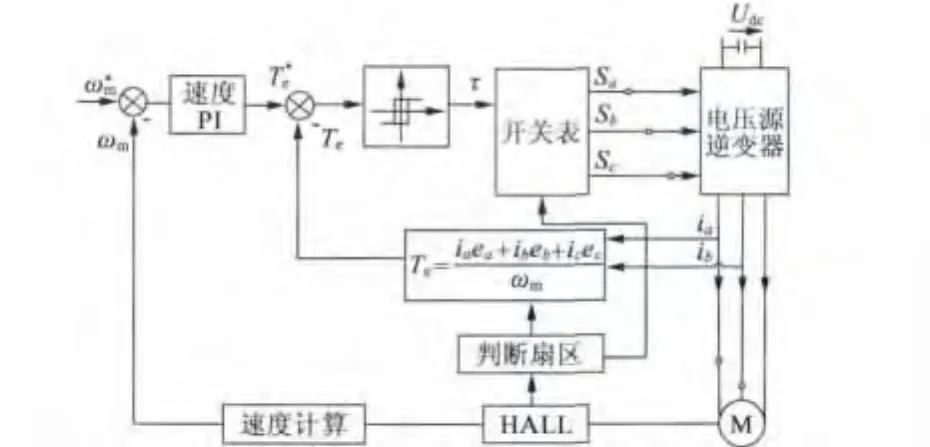
图8 无刷直流电动机直接转矩控制系统

图8中，Sa、Sb、Sc分别为三对功率管开关信号，、ωm、Te、、τ分别为给定转速、实际转速、实际转矩、给定转矩和转矩调节信号。转矩Te可用式(2)计算得到:

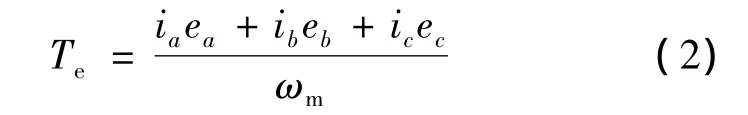
式中:ia、ib、ic分别为三相相电流，ωm为转子机械角速度，ea、eb、ec为相反电动势，可根据分段函数形式写出反电动势的表达式，此处以ea为例:

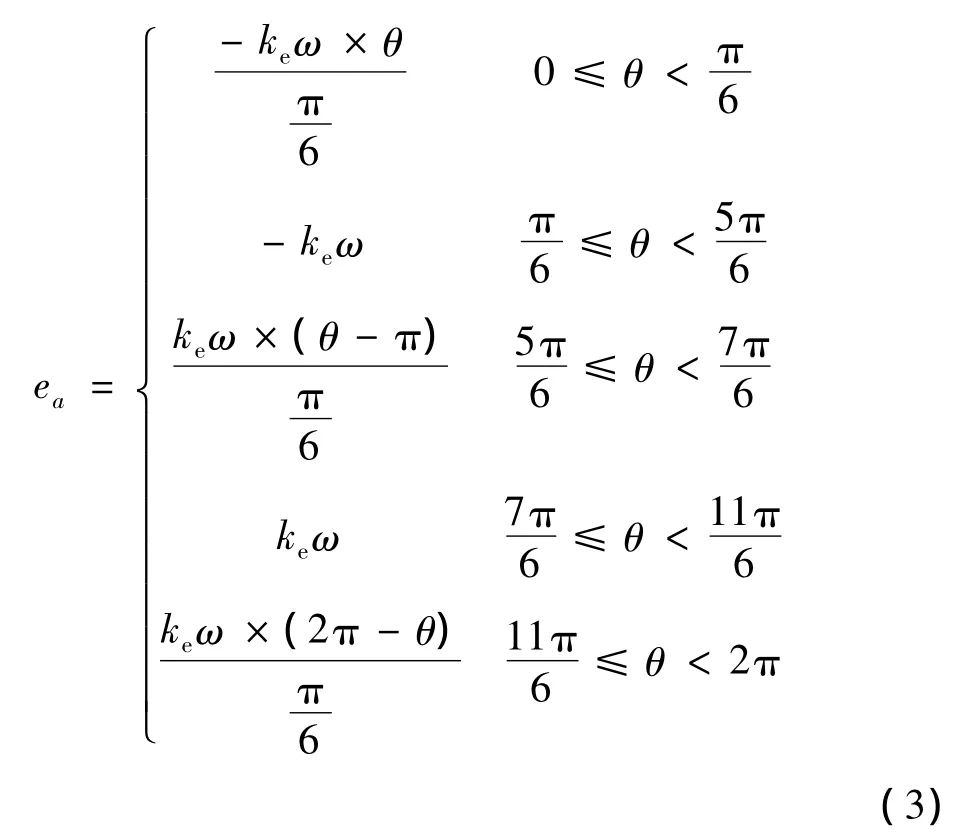
式中:ke为反电动势系数;ω为电角速度;θ为转子与α 轴夹角;eb、ec分别滞后 120°和 240°。

由图6中可以看出，在αβ坐标轴上，通过利用霍尔传感器的检测 30°、90°、150°、210°、270°和330°，然后延迟 15°或 45°，找到扇区边缘，依次为15°、45°、75°、105°、135°、165°、195°、225°、255°、285°、315°、345°，再按照相应的开关表控制逆变器。

实验使用的电机参数如表5所示。

表5 电机参数

电机转速约为3000 r/min，a相电流和转矩波形如图9所示。

由图9(a)可以看出，传统二二导通模式的直接转矩控制，由于6扇区的分区较宽，在换相过程中，存在着非换相电流即母线电流不平稳的问题，这将导致换相转矩脉动的增加。

由图9(b)可以看出，相比于传统二二导通模式的直接转矩控制，新型二三导通模式采用12扇区划分的直接转矩控制，可以有效降低换相过程对母线电流的影响，通过增加新的电压矢量细化扇区，令扇区之间的过渡得更加平稳，避免了扇区切换时，出现较大的电流波动，达到抑制转矩脉动的目的。

图9 采用不同DTC控制方式的a相相电流和转矩波形截图

通过比较由图9(a)和图9(b)的转矩波形图，可以直观地看到，相比传统二二导通模式，二三导通模式的直接转矩控制能有效地抑制转矩脉动，验证了理论分析的正确性。

5 结 语

二三导通模式可以通过增加电压矢量，细化扇区使无刷直流电动机换相过程更平稳，转矩脉动更小。本文通过结合二二导通和三三导通这两种模式，将传统的6电压矢量增加为12电压矢量，由于扇区的增加，可以在忽略复杂的磁链估算的前提下，对无刷直流电动机直接转矩控制进行改进。这种无刷直流电动机直接转矩控制简单，容易实现，在不加入复杂算法计算磁链的情况下，实现对无刷直流电动机的直接转矩控制的改进，12扇区的划分将使无刷直流电动机的直接转矩控制具有较高的研究价值。

［1］GAMAZO-REAL J C，VÁZQUEZ-SÁNCHEZ E，GÓMEZGILl J.Position and speed control of brushless DC motors using sensorless techniques and application trends［J］.Sensors，2010，10(7):6901-6947.

［2］DEPENBROCK M.Direct self-control(DSC)of inverter-fed induction machine［J］.IEEE Transactions on Power Electronics.1988，3(4):420-429.

［3］ZHONG L，RAHMAN M F，HU W Y，et al.Analysis of direct torque control in permanent magnet synchronous motor drives［J］.IEEE Transactions on Power Electronics，1997，12(3):528-536.

［4］LIU Y，ZHU Z Q，HOWE D.Direct torque control of brushless DC drives with reduced torque ripple［J］.IEEE Transactions on Industry Applications，2005，41(2):599-608.

［5］杨建飞，胡育文.无刷直流电机无磁链观测直接转矩控制［J］.中国电机工程学报，2011，31(12):90-95.

［6］高瑾，胡育文，黄文新，等.六边形磁链轨迹的无刷直流电机直接自控制［J］.中国电机工程学报，2007，27(15):64-69.

［7］王超，黄运生，韩华.新型无刷直流电机直接转矩控制［J］.电气传动，2011，41(8):20-23.

［8］BHARATKAR S S，YANAMSHETTI R，CHATTERJEE D，et al.Dual-mode switching technique for reduction of commutation torque ripple of brushless dc motor［J］.IET Electric Power Applications，2011，5(1):193-202.

［9］NOROOZI M A，MOGHANI J S，MONFARED J M，et al.An improved direct torque control of brushless DC motors using twelve voltage space vectors［C］//IEEE.Power Electronics and Drive Systems Technology(PEDSTC)，2012:133-138.