一类具非线性扩散系数的高阶中立型偏泛函微分方程的振动性

林文贤

（韩山师范学院数学与统计学系，广东潮州 521041）

1 引 言

20世纪80年代以来，由于生物遗传工程、化学反应过程、人口动力学及其它一些问题中出现了含时滞变元的偏微分方程，因而对于时滞变元的偏微分方程解的性态研究越来越受到人们的关注．部分作者对具有时滞的椭圆型、抛物型和双曲型偏微分方程的振动性进行了研究，如文献[1-15]，但对于高阶偏泛函微分方程振动性研究的文章较少[16-20]．本文将研究如下的具有非线性扩散系数的高阶中立型偏泛函微分方程

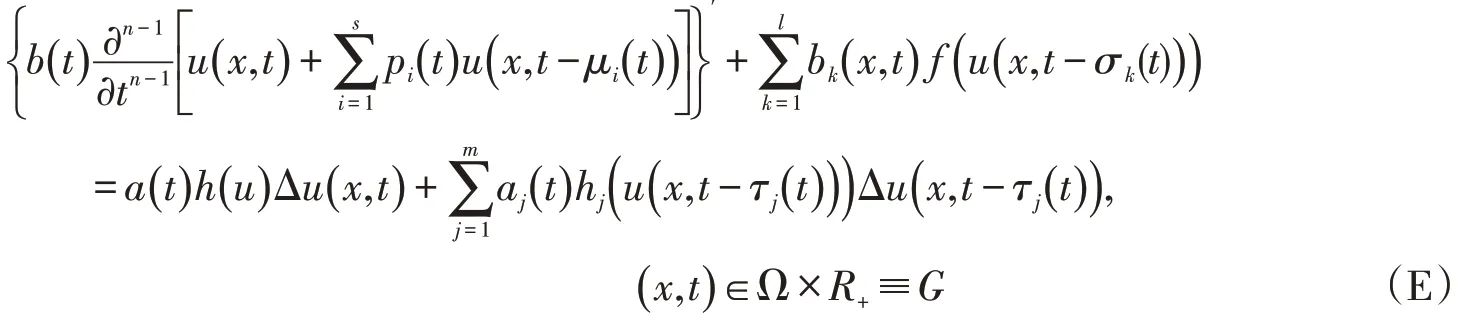
分别在边值条件

下解的振动性质，获得了其所有解振动的充分判据，结论充分表明了时滞量的决定性作用．其中n 为偶数， Δu 是RN中的Laplacian 算子， Ω ⊂RN是具有逐片光滑边界∂Ω 的有界区域， R+=[)0,∞ ,且ν 是∂Ω 的单位外法向量．当n=2,b()t ≡1 时，方程（E）就是文献[4]所研究的方程，因而本文的结论推广和包含了文献[4]的结果．

假设下列条件（H）成立：

引理1[21]设为常号，在上且满足则（i）存在ty≥t0使得y()i()t 在[)ty,∞上常号，i=1,2,…,n-1.

（ii）存在ℓ ∈{0,1,2,… }n-1 ，n+ℓ 为奇数，使得

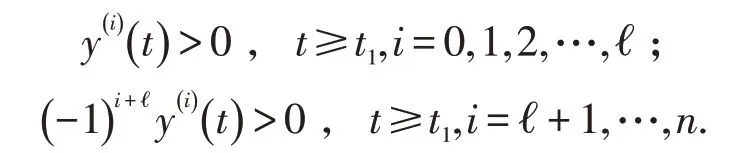
引理2[22]设满足引理1的条件，且则对每存在常数M ＞0使得

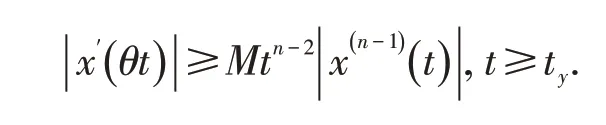
2 主要结果

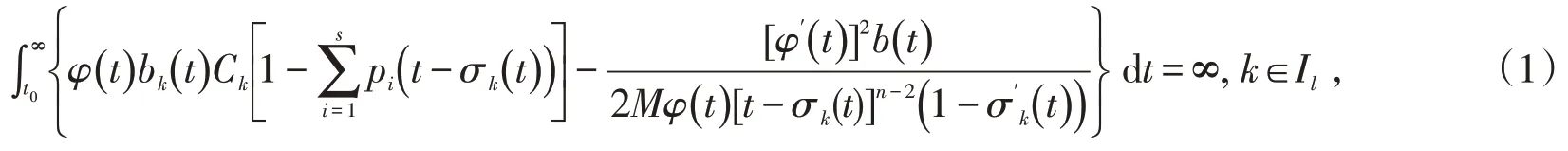
则边值问题（E），（B1）的所有解在G上振动．

证明 假设u(x,t)是问题（E），（B1） 的一个非振动解,不失一般性，不妨设的情形，令可类似证明）．由条件（H2），存在t1≥t0,使得当有

将方程（E）两边在Ω上关于x 积分，有

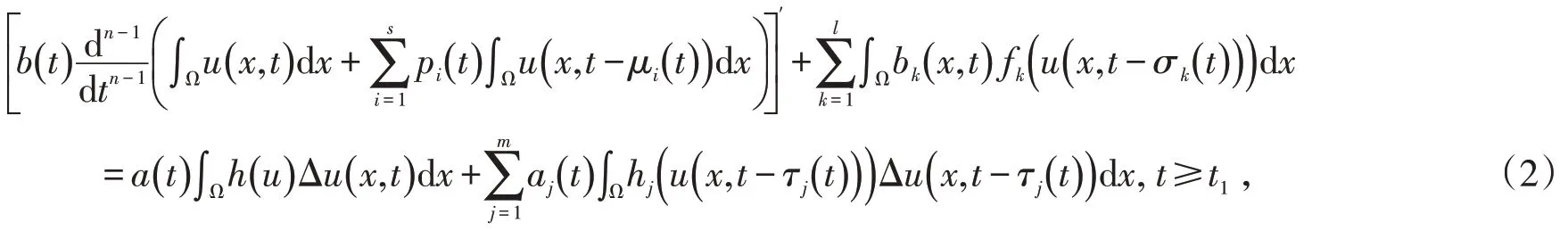
由Green公式和边值条件（B1）及（H3）得

其中dS 是∂Ω 上的面积元素．

又根据（H1），（H3）有

令V(t)=∫Ωu(x,t)dx，显然，于是由（2）-（5）可得

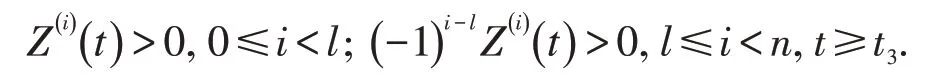
取i=1,得Z′()t >0,t ≥t3．于是，由引理1，存在t2≥t1，使得

又由（6）式有

从而有

进而，有

注意到（7）、（8）及（H2），由（10）得

令

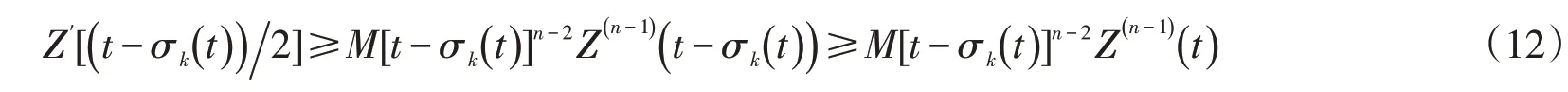
于是由（11），（12）式有

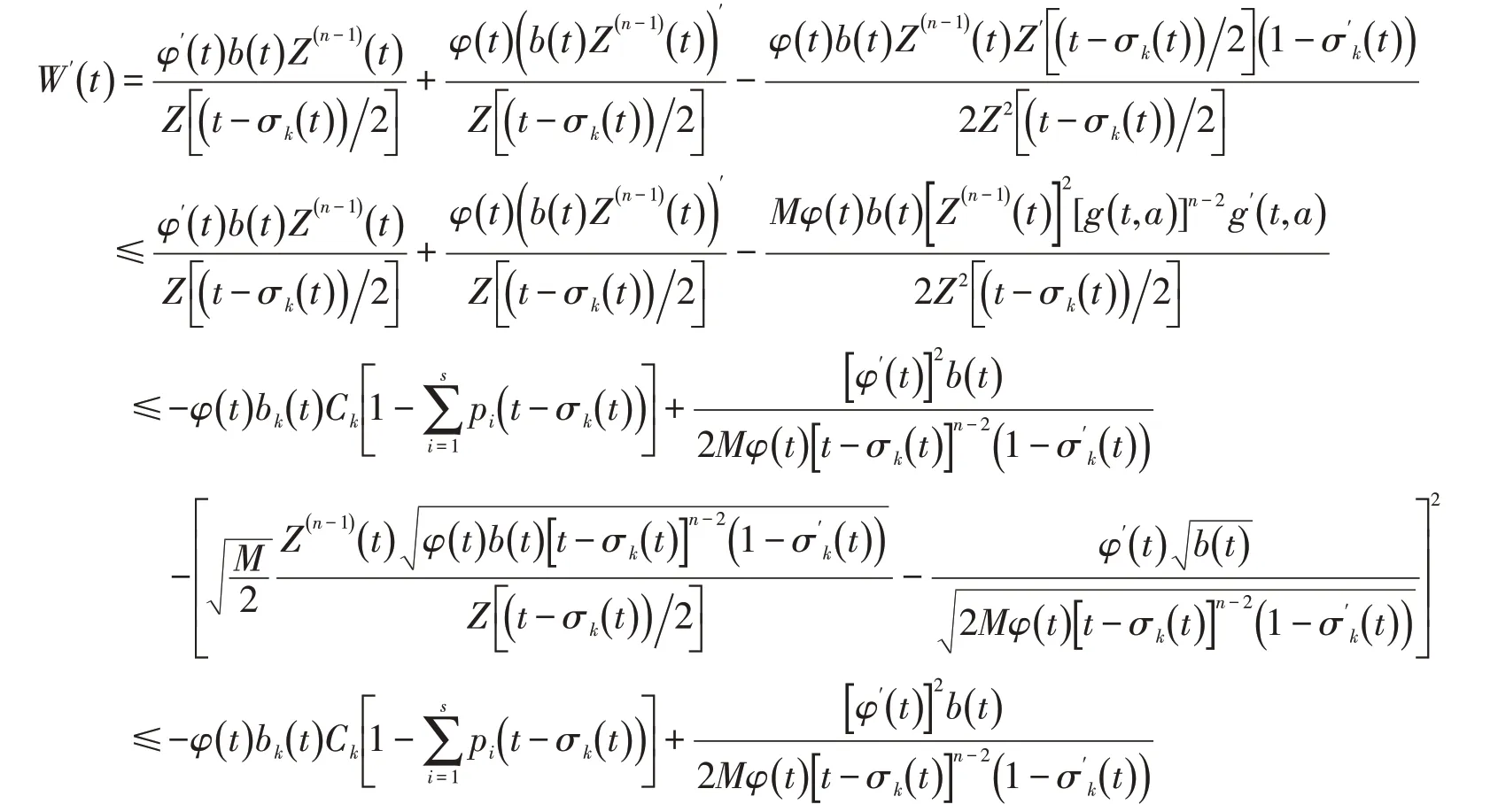
对上述的不等式从t2到t(≥t2)积分得

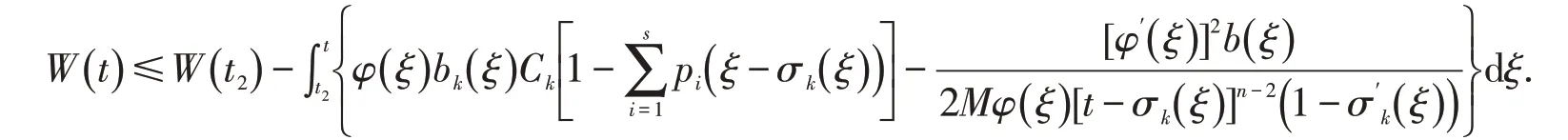
推论1 若将条件（1）换成微分不等式（9）无最终正解，则边值问题（E），（B1）的所有解在G上振动．

在定理1中，若φ(t)恒为正常数，则有

定理2 若将条件（1）换为

成立，则定理1的结论仍然成立．

引理3[23]设α0是如下Dirichlet特征值问题：

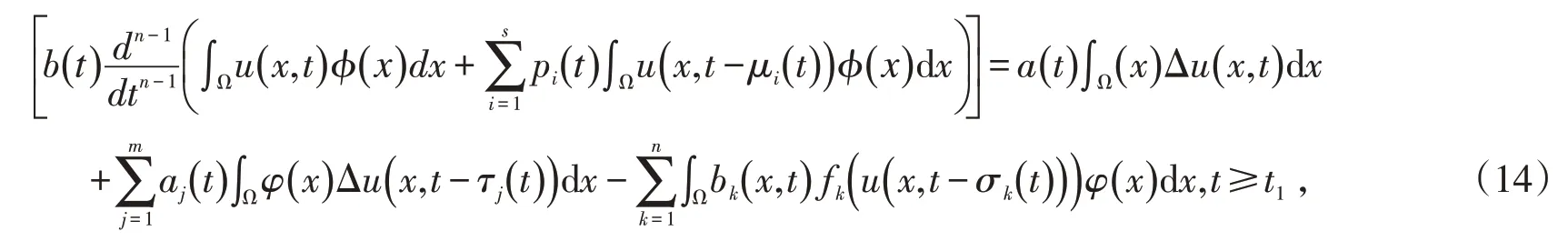
由Green公式和边值条件（B2）有

又由（H1）和（H2）有

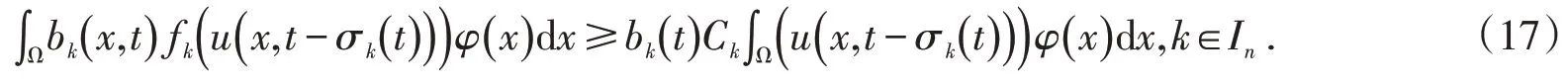
于是，由（14）-（17）有

因此得

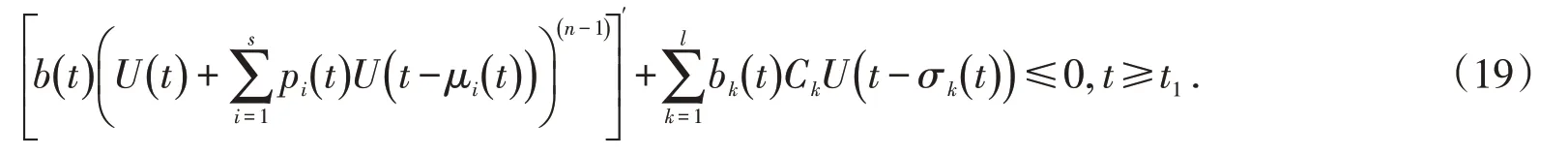
从而有

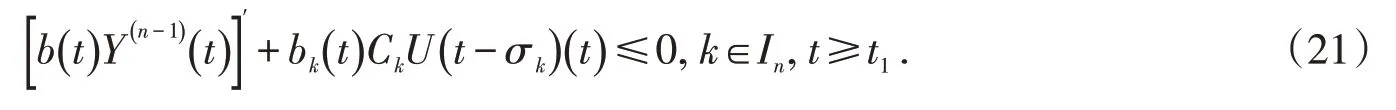
进而，有

令

于是由（23）和（24）式有

对上述的不等式从t2到t(≥t)2积分得

由微分不等式（18）有

类似于定理1的证明，可得如下结果：

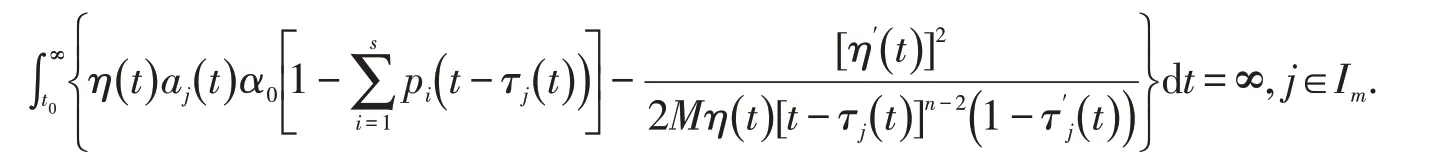
则边值问题（E），（B2）的所有解在G上振动．

[1]LIN Shi-zhong，ZHOU Zheng-xin，YU Yuan-hong．Oscillation criteria for a class of Hyperbolic differential equations continuous distributed deviating arguments[J]．J.of Math.(PRC),2005，25（5）：521-526．

[2]MISHER D P.Necessary and sufficient conditions for oscillation of neutral type parabolic differential equations[J]．Comptes Kendus Acad.Bulg.Sci.,1991，44（3）：11－15.

[3]王培光，葛渭高．一类非线性偏泛函微分方程的强迫振动性[J]．系统科学与数学，2000，20（4）：454-461．

[4]罗李平．非线性中立双曲型偏泛函微分方程的振动性定理[J]．数学杂志，2010，30（6）：1023-1028．

[5]何猛省，高述春．双曲时滞偏微分方程解的振动性质[J]．科学通报，1992，37（13）：1163-1166．

[6]林文贤．一类非线性中立型双曲方程的强迫振动性[J]．韩山师范学院学报：自然科学版，2002，23（2）：11-18．

[7]林文贤．一类二阶中立型偏泛函微分方程的振动性[J]．数学的实践与认识，2007，37（20）：192-195．

[8]林文贤．一类具连续偏差变元二阶中立型偏泛函微分方程的振动性[J]．韩山师范学院学报：自然科学版，2007，28（3）：8-10．

[9]林文贤．一类中立型双曲微分方程的振动性定理[J]．应用数学，2009，22（3）：514-519．

[10]林文贤．具连续偏差变元的非线性中立双曲型偏泛函微分方程的振动性[J]．韩山师范学院学报：自然科学版，2011，32（3）：8-12．

[11]林文贤．一类非线性中立双曲型偏泛函微分方程的振动性[J]．安徽大学学报:自然科学版，2011，35（3）：9-13．

[12]林文贤．一类具分布式偏差变元中立双曲型偏泛函微分方程的振动性[J]．南京师大学报：自然科学版，2011，34（4）：13-16．

[13]林文贤．一类具连续偏差变元的非线性中立双曲型偏泛函微分方程的振动性[J]．昆明理工大学学报:自然科学版,2012，37（1）：90-94.

[14]林文贤．一类具分布时滞的中立型双曲方程的振动性[J]．安徽大学学报：自然科学版，2013，37（6）：8-12．

[15]林文贤．关于一类非线性中立双曲型偏泛函微分方程的振动性的注记[J]．韩山师范学院学报：自然科学版，2013，34（3）：7-11．

[16]林文贤．一类高阶中立型偏微分方程的振动性[J]．西南师范大学学报，1998，23（1）：25-30．

[17]林文贤．高阶非线性中立型偏微分方程的振动性[J]．生物数学学报，2003，18（1）：8-14.

[18]林文贤．一类高阶中立型偏泛函微分方程的振动性[J]．黑龙江大学学报：自然科学版，2006，23（4）：449-456.

[19]林文贤．关于一类偶数阶中立型偏泛函微分方程的振动性的注记[J]．数学的实践与认识，2008，38（20）：239-242.

[20]林文贤．一类具有扩散系数和连续偏差变元的中立型偶阶偏泛函微分方程的振动性[J]．中国科学院研究生院学报，2012，29（6）：738-742.

[21]AGARWAL R P，GRACE S R，D.O’Regan.Oscillation Theory for Differential Equations[M]．Kluwer Academic,Dordrecht，2000.

[22]PHILOS Ch G．A new criterion for the oscillation and asymptotic behavior of delay differential equations[J]．Bull.Acad.Pol.Sci.Ser.Sci.Mat.，1981，39（1）：61-64.

[23]VLADIMIROV V S.Equations of Mathematical Physics[M]．Moscow：Nauka，1981．