基于规则三角网的等值线追踪与填充算法的实现和应用

2014-10-29廖国忠梁生贤吴文贤

物探化探计算技术 2014年1期

廖国忠，张伟，梁生贤，吴文贤，李富

（中国地质调查局成都地质调查中心，成都 610081）

0 引言

随着地质科学的发展，等值线图在矿产普查与勘探中的作用越来越大。等值线研究是科学计算可视化的一个基础而重要的内容，等值线图在物化探的信息提取、矿产勘查的定量化计算中发挥着重大作用［1－5］。

当前最常见的等值线追踪算法是基于规则矩形网格，以规则矩形网格为最小单元，连接网格边上的交点来实现［6－10］，但是当一个四边形中的交点达到四个时，这种算法将为等值线追踪带来不确定性（图1（b））。因此作者在此算法上进行了修改，将网格四边形划分为上、下两个三角形，一个三角形中要么有两个交点，要么没有交点，连接两个交点便确定一条直线，确保了等值线的唯一性（图1（c））。

1 算法设计

1.1 数据结构定义

为了克服基于规则矩形网格追踪算法带来的不确定性，作者在本文中，提出用矩形网格的对角线将矩形网格划分为上、下两个小三角形，在同一个三角形中，等值线与三角形的边要么没有交点，要么有两个交点。虽然矩形网格有两条对角线，但如果当所有的网格都选择同一方向的对角线，则就消除了划分三角形的不确定性。新定义的数据结构如图2所示。

1.2 求取等值线与三角形边的交点

三角网格各个顶点的坐标及值是已知的，等值线不总是在顶点上，为了更精确地查找到等值线与三角形边的交点，首先筛选出与等值线有交点的三角网格，然后分别在三条边上利用一次线性插值确定等值线与边的交点［7］（图3）。

交点坐标计算公式为式（1）。

1.3 追踪交点并将连接组成等值线

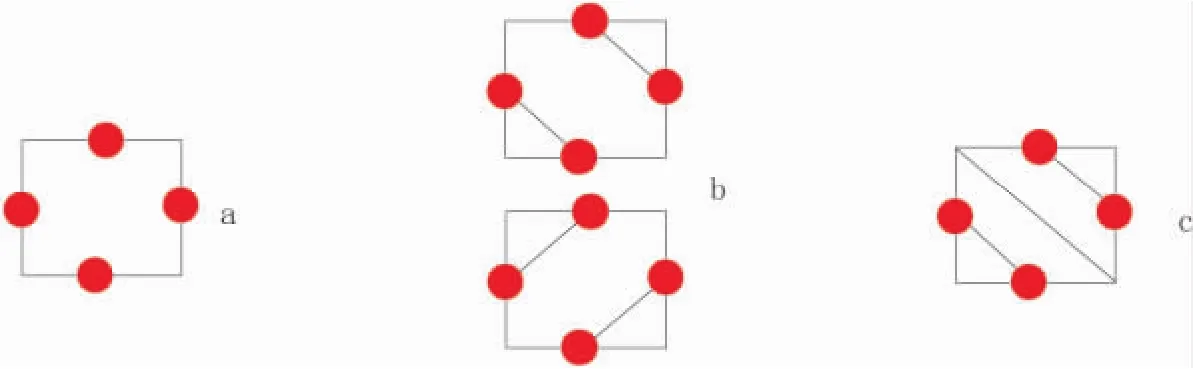
图1 矩形网格不确定性和三角网格的唯一性Fig.1 Uncertainty of the rectangular grid and uniqueness of the triangle grid

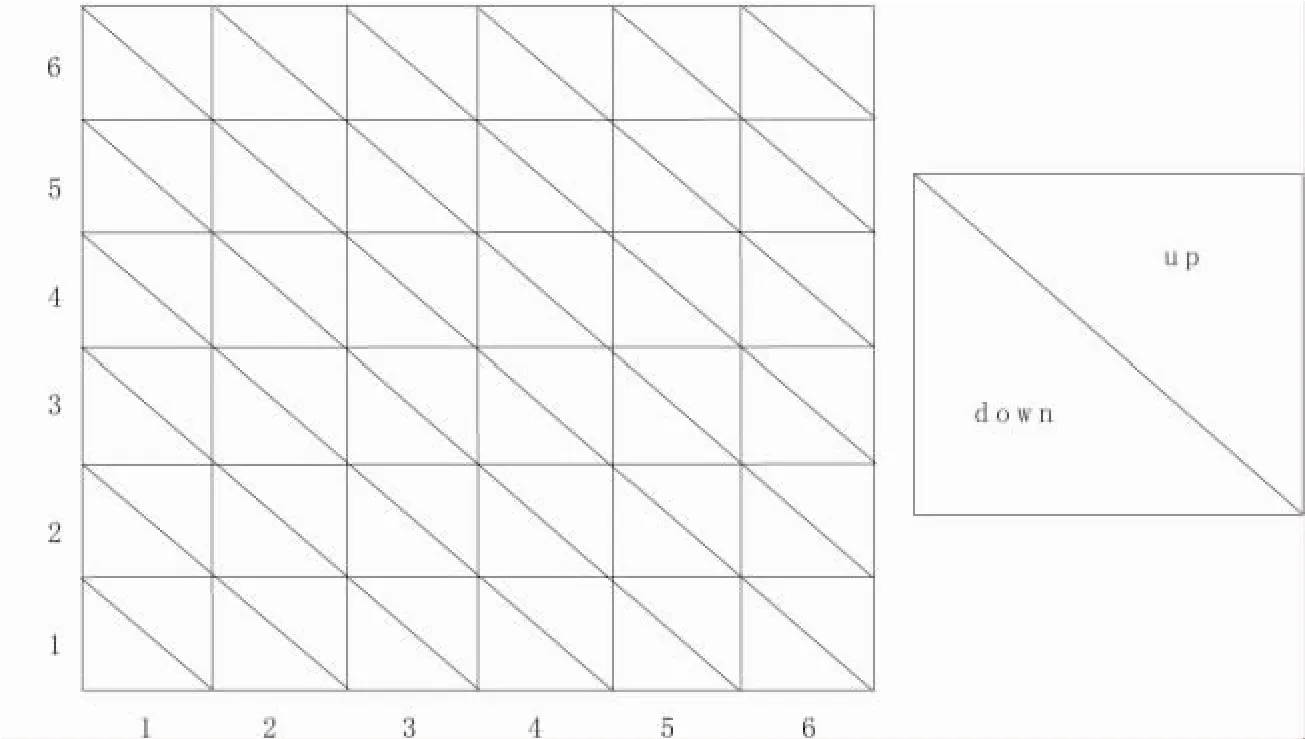
图2 规则三角网的数据结构Fig.2 Data structure of triangular network

图3 确定边与等值线的交点Fig.3 Determine the intersection of the edges and contours

等值线追踪遵循原则：①先追踪与整个网格的边相交的不闭合等值线，再追踪与整个网格的边不相交的闭合等值线；②不闭合等值线追踪，从左下右上的顺序查找边界上的交点作为起始追踪点；③闭合等值线追踪，从下而上的寻找交点作为起始追踪点［8，11－13］。

当得到起始追踪点A后，直接连接同一三角形的另一交点B既可，然后再查找共用交点B所在的边的另一个三角形，并以B作为下一个三角形的起始追踪点，如此类推，依次得到的交点便是等值线的节点，追踪过程如图4所示。

1.4 填充等值线

（1）首先将整个网格的四个角点组成的矩形，以最小值对应的颜色进行填充。

（2）填充不闭合等值线，按左下右上的顺序，找到不闭合等值线的线头，已知线头后便可知线尾，然后从线尾出发，按逆时针方向查找整个网格的四个角点，将线尾和线头间的网格的角点与等值线的节点组成一个多边形，然后以此等值线值所对应的颜色进行填充。

（3）最后将闭合等值线的节点组成一个多边形，以此等值线值所对应的颜色进行填充。

2 软件实现及测试

图4 等值线追踪过程Fig.4 Process of contour tracing

根据上面的算法设计，在 Microsoft Visual C＋＋6.0开发环境下，运用C＋＋这种面向对象的程序设计语言［14－15］，开发完成了基于规则三角网等值线追踪、填充的软件，并且利用横坐标范围为“0”到“100”，纵坐标范围为“0”到“100”，值的范围为“1.5”到“2.5”为基数，随机产生的1 000个离散数据，先利用surfer9网格化，然后将本软件实现的等值线追踪填充结果与sufer 9成图进行对比（图5）发现，除了两个软件绘制的色彩不现外，其图效果几乎一致，从而证明了本软件不仅实现了等值线追踪填充的目的，同时也证明了算法的正确性和高效性。

3 软件应用

将编制成功的软件，应用于区域地球物理调查成果集成与方法技术研究项目中的EH4电阻率反演剖面，利用本软件成图后的结果见图6。此EH4测线方向在地表垂直于断裂，通过EH4大地电磁测深反演后，利用本软件成图，图6中对断裂显示清晰，不同电性的地下地质体界面清晰。

4 总结

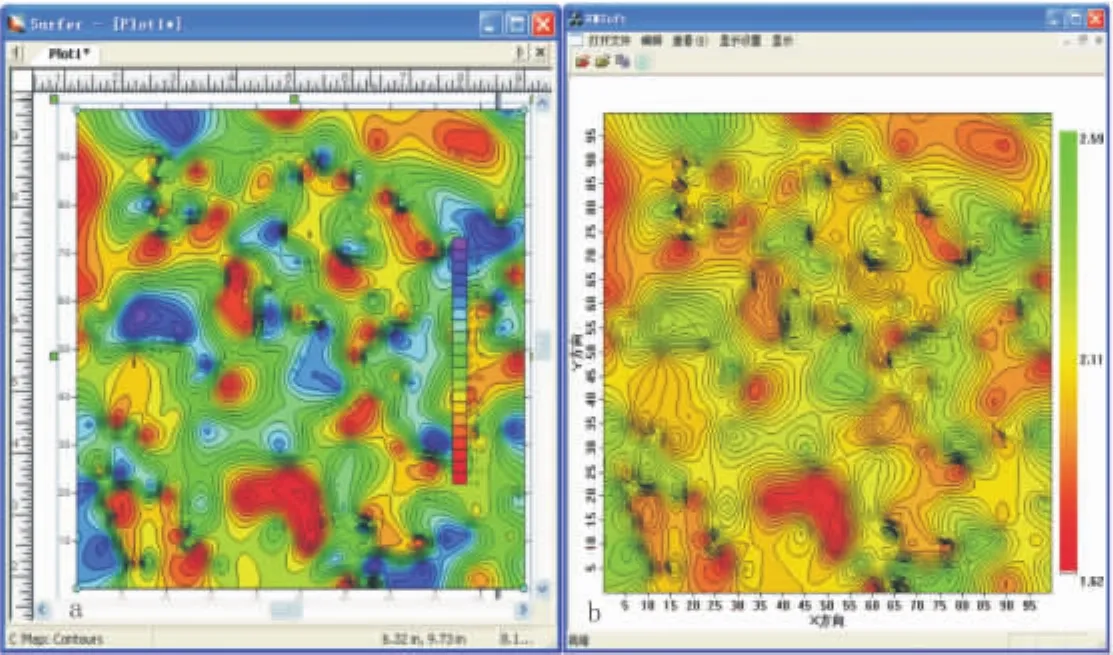
图5 对比本软件与surfer 9成图效果Fig.5 The software and surfer9comparison of drawing effect

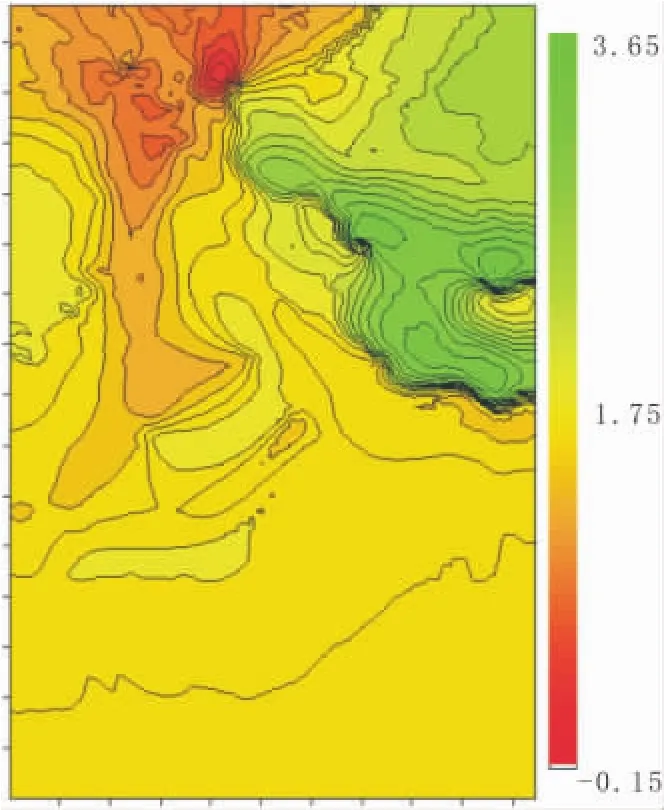
图6 EH4电阻率反演剖面图Fig.6 Inversion profile chart of EH4 electrical resistivity

作者围绕着基于规则三角网格等值线追踪算法，利用C＋＋面向对象语言，在 Microsoft Visual C＋＋6.0环境下，成功地编制了基于规则三角网格等值线成图软件，通过与成功商业软件surfer9的效果对比，显示了本软件有很好的成图效果，等值线追踪速度快，不存在等值线相交的错误。最后将此软件应用于实际物探资料显示中，得到很好的效果。虽然算法已经实现，但目前只能对规则的网格进行追踪，对于有空洞或者不是长方形的数据还不能进行追踪；色标只能在程序中设定，缺少接口进行交互式设置；等值线的等级不能交互式设置；标注也还没有实现，总之软件还需要更多的完善。

［1］李欢，奚小双，吴城明.关于地质等值线图绘制的几个问题［J］.科技信息，2009（34）：71－72.

［2］陈永辉，卢德唐，黄丰.地质构造等值线原理及实现技术［J］.计算机应用与软件，2006（04）：83－84，119.

［3］胡祥云，胡祖志，钟宏伟，等.科学可视化及其在地学中的应用［J］.工程地球物理学报，2004（04）：358－362.

［4］郭长春.“等值线”教学探究［J］.黑龙江科技信息，2010（17）：177－178.

［5］夏健明.绘制规则离散点等值线的一种算法［J］.计算机工程与设计，2003（09）：94－96.

［6］孙桂茹，马亮，路登平，等.等值线生成与图形填充算法［J］.天津大学学报，2000（06）：816－818.

［7］吴天毅.矩形网格节点上的插值函数［J］.天津科技大学学报，2008，23（3）：83－86.

［8］于嘉，吴旭.一种改进的矩形网格等值线追踪算法［J］.河南师范大学学报：自然科学版，2008（06）：34－36.

［9］李水乡，陈斌，赵亮，等.快速Delaunay逐点插入网格生成算法［J］.北京大学学报：自然科学版，网络版，2006，1（3）：302－306.

［10］孙科峰，孙根正，李洁.一种新的矩形网格生成等值线算法［J］.东华大学学报：自然科学版，2005（04）：66－69.

［11］于黎.等值线的跟踪绘制［J］.石油工业计算机应用，1997（04）：18－19.

［12］何生存，郭三刚，刘珍花，等.离散点数据插值方法及等值线绘制技术的应用［J］.青海科技，2006（4）：24－26.