FrFT解线调浅剖信号增强算法及FPGA实现

朱建军，李海森，杜伟东

(1.哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001;2.哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001)

长期以来，Chirp浅剖声呐是进行海底浅地层结构探测和属性识别的重要声学遥测设备［1］，主要采用滤波和脉冲压缩等常规信号处理手段［2］。通常浅剖信号中混杂有较强的带内随机噪声干扰，影响了浅剖声呐的探测性能和探测效果，严重时甚至会造成地层结构误判和参数错误估计［3］。采用信号增强技术提高信号信噪比是改善浅剖声呐成图质量和浅地层属性识别准确性的有效途径之一。目前浅剖资料的噪声抑制研究主要集中在采用中值滤波、邻域平均法、频域滤波等方法的图像降噪领域，针对原始信号的研究较少。

经典信号增强方法是将含噪信号投影至互不重叠的噪声子空间和信号子空间，通过保留信号子空间实现信号增强［4］，研究主要集中在基于奇异值分解、Cohen类时频变换、自适应滤波以及各种理论相结合的信号增强方法［5-7］。基于奇异值分解的信号增强方法在低信噪比时不能确定有效的秩，难以实现信号和噪声子空间分离;虽然文献［8］联合STFT和奇异值分解取得了较好的信号增强效果，但仅具有单分量Chirp信号增强能力;而基于Cohen类时频变换的信号增强方法在处理多分量、多途信号时普遍存在交叉项干扰;自适应滤波虽可以通过自动调整滤波参数实现最优滤波，但其渐近收敛特性在样本较少时会导致输出信号起始部分误差显著。FrFT是一种线性时频变换技术，适合多分量信号处理，将Chirp信号由时域变换至分数阶 Fourier域(该表示域通常用u-v坐标系描述，与传统t轴表示时域类似，u轴代表分数阶Fourier域，常简称u域)时具有良好的能量聚集性。针对具有多途信号特征的Chirp浅剖信号，提出一种基于FrFT解线调理论的浅剖信号增强算法，利用FrFT Chirp解线调信号在u域表现为能量聚集的线谱信号而白噪声仍为白噪声的特性，采用时频域带通滤波和u域遮隔联合处理实现信号与噪声间的去耦，达到信号增强的目的，最后在FPGA上进行算法实时实现研究。

1 FrFT解线调原理

1.1 单分量Chirp信号解线调

FrFT是广义的Fourier变换，可解释为信号时频平面绕原点逆时针旋转某一角度后的分数阶Fourier域表示，信号s(t)的FrFT定义为［9］

式中:α=pπ/2为时频坐标系旋转角度，p为变换阶数;Kα(t，u)为 FrFT 的变换核，分数阶 Fourier逆变换(IFrFT)表示为Sα(u)的p阶FrFT。另外，FrFT为线性变换，具有阶数可加性(又称旋转相加性，FpFq=Fp+q)、时移、频移等特性［10］。FrFT 的处理结果主要取决于参量α，由FrFT定义及性质可推得Chirp信号s(t)=exp［j(ωt+kt2/2)］的p阶FrFT。

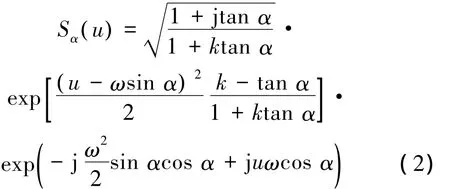
式中存在一个特殊的旋转角度—Chirp信号时频分布与时间轴的夹角αc=arctan k，k为Chirp信号调斜率。当t-f坐标系(时频域)逆时针旋转αc角度至u-v坐标系(u域)时，Chirp信号将转变为u域上的单频信号，去除了频率的线性调制，该变换过程的原理如图1所示。其中，fL为Chirp信号的起始频率，V0为解线调信号对应u域信号的频率，T为信号脉冲宽度。

图1 Chirp信号解线调原理Fig.1 Principle of chirp signal dechirping

由式(2)可知，当α=αc时:

式中:W 为常数，exp(j uωcosαc)是单频信号，即Chirp信号经αc角度的FrFT后转变成了u域单频信号，实现了Chirp信号的解线调。

1.2 多途信号FrFT解线调

由FrFT的线性可加性和时延特性，多途信号x(t)旋转αc角度的FrFT为

式中:Ai为常系数，τi为第i个回波信号的时延，M为多途路径数。与单分量Chirp信号解线调原理相同，经过αc角度的旋转，多途信号在u域变为一系列的线谱信号。为说明时延与解线调信号u域频率的对应关系，忽略多普勒效应影响(认为各多途信号分量调斜率相同)。由式(4)可知，无论正调斜率还是负调斜率Chirp信号，其解线调信号的u域频率均将随时延的增大而减小;由于具有相同的理论表达式，Chirp多途信号解线调原理图仅给出正调斜率的情况，如图2所示，时延为τi的信号分量对应的u域频率Vi，T为时间窗长度。

图2 Chirp多途信号FrFT解线调Fig.2 Multi-path chirp signal dechirping based on FrFT

2 解线调信号u域频谱特征分析

2.1 u域线谱频率

由上文分析可知，解线调u域信号频率的大小主要由时延、起始频率、调斜率及时窗长度4个参量决定。由图2中Chirp信号时频域及u域分布位置几何关系、量纲归一化理论及FrFT算法原理，推得时延为τ的Chirp解线调信号的u域频率为:

式中:Δ表示量纲归一化值，S=sqrt(T·fs)为量纲归一化时间因子［11］。

对于Chirp多途信号，随着时延增大其解线调信号的u域频率会出现负值，如图2中最大时延分量。为了与传统时频域频谱理论相统一，同时也便于理论分析，将解线调信号频域的原点选为u域v轴的起始点，即解线调信号的u域频谱均为正值。

2.2 解线调多途信号u域频带范围

由式(5)及FrFT解线调理论可知，解线调处理将多途信号由宽带信号转变为线谱信号的同时，也使各谱线较集中地分布在小于u域宽度的有限频带范围内，从而后续u域信号处理可有针对性地在这一区域进行，这样既消除了该区域外噪声对算法性能的影响又减小了计算量。为了说明这一现象，以fs=40 kHz、时间窗为4倍脉宽(4T)、起始频率为2 kHz的Chirp信号为例，给出不同调斜率下解线调信号u域频率范围随时延τ的变化关系，如图3所示，横轴为时延与脉宽的比值(τ/T)，纵轴为u域频率。同时也表明，调斜率越小线谱分布越集中。

图3 解线调信号u域频率范围随时延的变化关系Fig.3 Relationship between time delay and dechirp signal u domain frequency range

解线调后多途信号分量的u域频率将随时延的增加逐渐减小，即最小时延分量的u域频率对应解线调线谱分布频率范围的上限、最大时延分量的u域频率对应分布范围的下限，则解线调Chirp多途信号的u域频带范围Rdechirp可表示为

式中:τmax和τmin分别为多途信号分量的最大和最小时延值。为了说明影响解线调多途信号u域频带范围的因素，进一步推得多途信号u域分布频带宽度Bdechirp为

由式(7)可知，当时间窗确定后，解线调多途信号的u域分布仅与时延差和调斜率有关，与时间窗选取位置无关，即时间窗位置不会影响解线调信号u域频带宽度。图3也说明了这一点，曲线斜率不变表明相同大小的时延差对应相同的u域频带宽度，而与时间窗的选取位置无关。从而可将采集样本序列划分为多个相等长度的子时间窗，逐个进行处理，而得到性能一致的处理结果。

3 浅剖信号增强算法

3.1 信号增强原理

由于Chirp信号为宽带信号，基于加窗技术的传统带通滤波方法无法去除带内信号与噪声间的耦合［8］。Chirp信号FrFT解线调后变为能量聚集的线谱信号，而白噪声仍为白噪声且仍分布在几乎整个u域上［12］，因此，解线调处理在u域上进一步去除了信号与噪声间的耦合，从而采用遮隔处理提取信号信息实现了信号增强。本文提出的浅剖信号增强方法包括2个过程:1)时频域带通滤波，提高了u域信号的输入信噪比;2)u域频谱遮隔，进一步抑制了带内噪声成分。因此，两处理过程的有机结合取得了传统时频域滤波方法无法达到的信号增强效果。FrFT解线调浅剖信号增强算法的增强原理如图4所示，斜线区为常规带通滤波作用区域，网格区为u域遮隔作用区域。

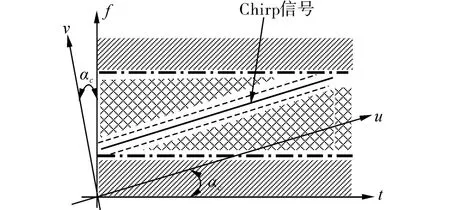
图4 FrFT解线调信号增强原理Fig.4 Princip le of FrFT dechirping signal enhancement

3.2 算法流程

根据信号增强原理，FrFT解线调浅剖信号增强算法的算法流程如图5所示。

图5 FrFT解线调浅剖信号增强算法流程图Fig.5 Flow chart of sub-bottom pr of iling signal enhancement algorithm based on FrFT dechirping

为了得到u域线谱，信号需采用解析形式。由FrFT阶数可加性，本算法中的“FrFT解线调”与“FFT”可合并为一次2αc/π+1阶 FrFT;同理，“IFFT”与“FrFT 反解调”也可合并为一次-2αc/π-1阶IFrFT。频谱遮隔在u域进行，即针对解线调信号的频谱进行遮隔，其算法流程如图6所示。

图6 u域频谱遮隔算法流程图Fig.6 Flow chart of spectrum masking algorithm in u domain

频谱遮隔处理首先限定浅剖信号的u域频带范围，以消除带外噪声影响并减小后续信号处理的计算量，然后对截取频谱进行平滑处理，消除频谱中的高频起伏成分，以准确确定遮隔门限η，最终根据遮隔门限对截取频谱进行遮隔处理。

4 仿真实验及算法FPGA实现

4.1 浅地层分层结构建模

Chirp浅剖回波信号包含了不同沉积层界面的反向散射信号，是典型的多途回波信号。为了验证提出算法，建立典型的浅地层分层模型，需满足以下约束条件［13］:

1)沉积层相互平行，且每层水平方向各向同性;

2)沉积层界面反射系数与频率无关;

3)忽略声衰减引起的脉冲展宽，但计入声衰减对信号能量的影响;

4)平面声波垂直地层入射，从而在不考虑水声信道时散和多普勒效应的情况下，Chirp浅剖回波信号可表示为发射信号与沉积层冲激响应的卷积:

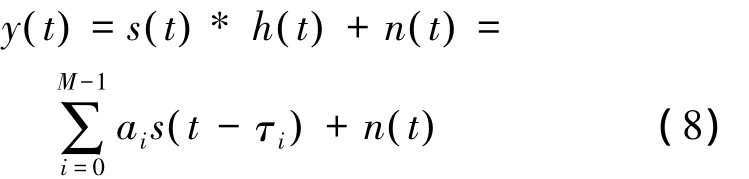
式中:s(t)为发射信号，h(t)为沉积层冲激响应，n(t)为噪声，M、ai和τi分别为分层数量、第i层回波的“幅度”(包括极性信息)和时延。沉积层分层模型如图7所示，其中ρi ci为第i层沉积层声阻抗。

图7 浅地层模型几何结构Fig.7 Sub-bottom model geometry

4.2 算法性能仿真

以浅地层分层结构模型构造浅剖回波信号，对算法进行计算机仿真研究。以由4个地层反射且时域波形发生混叠信号作为浅剖回波信号，发射信号为脉宽3 ms、2～4 kHz的Chirp信号，浅地层归一化冲激响应幅度0.43、1、-0.71和0.83均匀随机产生，对应时延为 1、1.5、2.4、3.2 ms，fs=28 kHz，SNR=0 dB。沉积层冲激响应、带通滤波输出浅剖信号的波形与频谱如图8，由图8(c)可以清楚地发现，浅剖信号存在大量带内噪声，且难以区分各回波分量。

利用提出的信号增强算法对上述回波信号进行处理，得到解线调及遮隔处理各阶段的u域频谱如图9所示。解线调后信号变为集中分布的线谱，而带内噪声大范围地分布在u域上，表明解线调进一步去除了信号与带内噪声间的耦合;经u域频谱截取和平滑处理后确定遮隔门限，可遮隔得到含有较少噪声成分的u域信号频谱图9(d);最终通过IFr-FT即可得到增强后的时域信号。

图8 浅地层冲激响应和浅剖信号的波形及频谱Fig.8 Waveform and spectrum of sediment im pulse response and sub-bottom pr of ile signal

图9 浅剖信号u域遮隔处理Fig.9 u domain masking of sub-bottom pr of iling signal

图10给出了上述仿真信号在4种不同情况下的相关空间波形。由带通滤波前后相关空间波形发现，时频域带通滤波难以消除带内噪声，同时也表明了进行带内噪声抑制的意义及必要性。经信号增强算法处理的信号带内噪声得到了进一步的有效抑制，可有效提高信号信噪比。

图10 信号相关空间波形Fig.10 Signal wave form in correlation space

在上述仿真条件下，采用Monte Carlo方法对信号增强算法处理前后相关空间信号输出信噪比进行5 000次统计实验，得到其随输入信噪比的变化曲线，如图11所示。其中，输出信噪比为［14］

实验结果表明本信号增强算法在输入信噪比小于5 dB的情况下能够带来3～4 dB的信噪比改善。

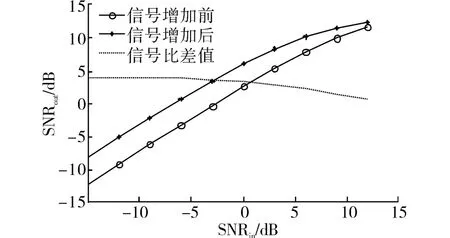
图11 相关空间信号信噪比统计曲线Fig.11 SNR statistical cures in correlation space

4.3 信号增强算法FPGA实现

4.3.1 算法计算量分析

提出信号算法增强算法主要包括实信号滤波、解析信号求解、DFrFT、频谱遮隔(频谱截取、平滑、门限判定、遮隔)和IDFrFT运算。主要运算量分析如下:假设信号采集样本点数N=2n(n为整数)，FIR滤波器阶数为L，则需进行LN/2次乘法运算和(L－1)(N-1)次加法运算;解析信号求解采用FFT实现，包括N点FFT和IFFT运算各1次以及N点乘法运算;DFrFT采用快速算法—分解法，其核心思想是利用FFT实现算法中的卷积运算，从而将运算量 由 O(N2)降 至 O(N lb N)，定 义 M=2int(lb［6(N+1)］)+1，则实现一次 DFrFT 需进 行 1 次2N－1点的复点乘、1次M点FFT、1次M点复点乘、1次M点IFFT和1次N点复点乘，IDFrFT为DFrFT的逆变换，运算量与DFrFT相同;频谱遮隔处理中频谱截取、遮隔等过程均根据索引号进行数据判选，平滑处理(K点平滑)计算量也较小。另外，所有滤波系数及DFrFT计算用到的辅助变量均在算法实现前完成预存储，不考虑其计算量。计算量统计见表1。

表1 算法主要步骤计算量Table 1 Calculation amount of main procedure step

4.3.2 算法实时实现

高分辨Chirp浅剖声呐设计探测深度小于等于50m(取决于底质、频率和噪声级)，fs=28 kHz，最大浅剖深度时处理样本点数约1 900点(由设置量程决定)。算法主要由卷积和FFT实现，而FPGA具有规整的内部逻辑块阵列和丰富的连线资源，特别适合实现FIR和FFT等具有高并行结构特点的数字信号处理。兼顾算法计算量，选择在1片ALTRA公司Stratix II系列FPGA EP2S180F1020上实时实现本算法，它有143 520 个ALUTs，96 个 DSP blocks，3 621 897 bits片上存储空间。设计主时钟为100 MHz，因此每个采样间隔可完成3 571个指令周期的运算。按照图5算法流程设计FPGA算法结构如图12所示，图中重复出现的DFrFT算法结构(如IDFrFT)以简化形式给出。

算法实时实现充分利用FPGA丰富的IP软核资源，主要调用FIR、乘法和FFT等Mega function。实信号FIR滤波采用23阶串行滤波器结构，以最少的逻辑资源实现滤波功能。由于时间窗位置的选取不会改变窗内信号分量的u域频带宽度，采用将样本序列划分成多子时间窗流水处理的方案;考虑解析信号采用FFT实现，设计对256个样本点的子时间窗求解解析信号，从而DFrFT和IDFrFT需做2 048点FFT。FFT运算均采用单输出结构和Burst I/O数据流设计，18 bits数据精度。辅助参量(DFrFT分解法权系数A、调制信号Chirp1、卷积信号Chirp2频谱，及式(6)计算的u域频谱截取索引号index1、index 2等)事先均存储于FPGA片上存储空间。算法实现使用逻辑资源及存储空间统计见表2。

图12 算法FPGA实现流程图Fig.12 Flow diagram of FPGA implementation

表2 算法实现使用资源统计Table 2 Resource accounting of algorithm im plementation

图13 增强前后浅剖信号匹配滤波输出包络Fig.13 Sub-bottom pr of iling signal matched filter output envelops before and after signal enhancement

经过Quartus综合编译和Time Quest时序分析得出，主时钟频率达到了124.23 MHz，表明100 MHz主时钟频率设计的合理性。同时在FPGA上对30 ms浅剖信号进行实时处理，得到信号增强前后匹配滤波输出信号包络如图13所示。

5 结论

在对FrFT解线调理论进行研究和理论推导的基础上，提出并实时实现了一种基于FrFT解线调理论的Chirp浅剖信号增强算法，得出以下结论:

1)FrFT解线调技术可在u域去除浅剖信号带内噪声与信号间的耦合，联合时频域带通滤波和u域遮隔处理可实现对浅剖信号带内噪声的有效抑制;

2)通过解线调信号频谱分析得出，时间窗位置不影响信号u域带宽和算法性能，从而可对采集信号分段进行并行处理，为工程实现提供了依据;

3)该信号增强算法结构适合于FPGA实现，为工程应用提供了技术储备和支持。

［1］TSENG Yaoting，DING Jianjiun，LIU Charshine.Analysis of attenuation measurements in ocean sediments using normal incidence chirp sonar［J］.IEEE Journal of Oceanic Engineering，2012，37(3):533-543.

［2］RAKOTONARIVO S，LEGRIS M，DESMARE R，et al.Forward modeling for marine sediment characterization using chirp sonars［J］.Geophysics，2011，76(4):91-99.

［3］赵铁虎，张志珣，许枫.浅水区浅地层剖面测量典型问题分析［J］.物探化探计算技术，2002，24(3):215-219.ZHAO Tiehu，ZHANG Zhixun，XU Feng.Analysis of typical problem for shallow acoustic surveying in the shallow waters［J］.Computing Techniques for Geophysical and Geochemical Exploration，2002，24(3):215-219.

［4］JARROT A，IOANA C，QUINQUISA.Denoising underwater signals propagating through multi-path channels［C］//Oceans 2005-Europe.(s.l.)，2005:501-506.

［5］张丽燕，殷福亮.一种改进的奇异值分解语音增强方法［J］.电子与信息学报，2008，30(2):357-361.ZHANG Liyan，YIN Fuliang.An improved speech enhancement method based on SVD［J］.Journal of Electronics ＆Information Technology，2008，30(2):357-361.

［6］陈小龙，关键，刘宁波，等.基于FrFT的LFM信号自适应滤波算法及分析［J］.现代雷达，2010，32(12):48-59.CHEN Xiaolong，GUAN Jian，LIU Ningbo，et al.Adaptive filtering algorithm for LFM signal and performance analysis based on FRFT［J］.Moden Radar，2010，32(12):48-59.

［7］林红波，李月，潘伟.时频峰值滤波信号增强方法在实际地震资料处理中的应用［J］.吉林大学学报:地球科学版，2007，37(5):1038-1041.LIN Hongbo，LIYue，PANWei.Application of signal enhancement method based on time-frequency peak filtering to seismic data processing［J］.Journal of Jilin University:Earth Science Edition，2007，37(5):1038-1041.

［8］邹红星，李衍达.基于时频面旋转的线性调频信号增强［J］.清华大学学报:自然科学版，1999，39(7):103-106.ZOU Hongxing，LIYanda.Enhancing chirp signal based on rotation of time-frequency plane［J］.Journal of Tsinghua university:Sci＆Tech，1999，39(7):103-106.

［9］张波，安天思，韩静，等.水下复杂目标宽带回波精细特征提取［J］.哈尔滨工程大学学报，2010，31(7):872-878.ZHANG Bo，AN Tiansi，HAN Jing，et al.Extracting fine details in broadband echoes from complex underwater targets［J］.Journal of Harbin Engineering University，2010，31(7):872-878.

［10］李丽，邱天爽.基于分数阶傅立叶变换的双基地雷达线性调频信号的参数联合估计新方法［J］.电子与信息学报，2012，34(4):878-884.LI Li，QIU Tianshuang.A novel method for joint paramteter estimation of LFM signals in bistatic MIMO radar system based on FRFT［J］.Journal of Electronics＆ Information Technology，2012，34(4):878-884.

［11］孙志国，李迎，陈晶，等.基于mTD-FrFT的VMFSLFM信号参数估计方法［J］.哈尔滨工程大学学报，2012，33(10):1310-1314.SUN Zhiguo，LIYing，CHEN Jing，et al.Parameters estimation methods of VMFS-LFM signals based onmTD-FrFT［J］.Journal of Harbin Engineering University，2012，33(10):1310-1314.

［12］陈鹏，侯朝焕，马晓川，等.基于匹配滤波和离散分数阶傅里叶变换的水下动目标LFM回波联合检测［J］.电子与信息学报，2007，29(10):2305-2038.CHEN Peng，HOU Chaohuan，MA Xiaochuan，et al.The joint detection to underwater moving target’s LFM echo based on matched filter and discrete fractional Fourier transform［J］.Journal of Electronics ＆ Information Technology，2007，29(10):2305-2308.

［13］QUINQUISA，RADOIE.FM pulses separation for improving sub-bottom attenuation estimation［C］//Oceans＇97.(s.l.)，1997:1359-1365.

［14］齐林，陶然，周思永，等.基于分数阶傅里叶变换的线性调频信号的自适应时频滤波［J］.兵工学报，2003，24(4):499-503.QI Lin，TAO Ran，ZHOU Siyong，et al.An adaptive time-frequency filtering method based on fractional Fourier transform for linear frequency modulation signlas［J］.Acta Armamentarii，2003，24(4):499-503.