适用于宽波束的多接收阵SAS波数域成像算法

张学波，唐劲松，钟何平，张森

(海军工程大学 电子工程学院，湖北 武汉 430033)

在多接收阵合成孔径声呐(SAS)系统［1-2］中，由于声呐平台速度和声速的可比拟性以及成像距离的增大，机载合成孔径雷达(SAR)中的“停-走-停”假设［3］不再成立，如果仍然忽略了非“停-走-停”［4］的影响，那么远距离目标可能出现畸变;而相位中心近似(PCA)［5］将多接收阵的信号转化为收发合置的形式，进而简化为传统收发合置SAS成像问题，然而这个转化会引入延迟误差，如果不加以补偿，会降低近距离目标的成像质量。

Yamaguchi［6］以目标区域中心为参考，用聚焦到目标中心点的相位误差来代替所有目标区域的误差，进而在距离弯曲校正过程中完成PCA误差的补偿，这会导致图像边沿模糊。Bonifant将这两个误差分开来考虑，并通过两个独立的相位项［7］来分别补偿非“停-走-停”和PCA误差，然而非“停-走-停”补偿未考虑距离向空变性的影响，仅对测绘带中心实现了精确补偿，并且其独立的误差分析方法还忽略了两个误差之间的耦合性。Callow认为宽波束内不同方向目标的PCA误差是不同的［8］，并用场景中心点目标方位空变的PCA误差来近似整个场景的方位空变误差，这仅对中心点目标实现了精确补偿，在边沿同样会出现模糊。杨海亮在深入分析这两类误差的基础上，提出了一种适用于宽测绘带的多接收阵SAS成像方法［4］;汪海涛等在精确时延模型基础上，也给出了类似的成像方法［9］;然而他们对非“停-走-停”和PCA的补偿是以波束中心为参考进行统一补偿的。实际上，对于发射阵元的每个发射脉冲，接收阵元接收到的数据对应的是整个波束内所有散射点的回波;波束很窄时，以波束中心为参考进行统一补偿能够取得较好的结果;然而当采用低频信号进行远距离探测时波束较宽，系统误差相对波束内不同方位位置的目标是不同的，如果仍采用窄波束假设进行处理，将会导致图像旁瓣抬高出现虚假目标、图像几何失真和对比度下降。

声呐在运动过程中观察目标的视角是不断变化的，而该侧视角与多普勒频率之间具有一一对应的关系。基于此，文中建立了考虑非“停-走-停”和PCA误差方位向空变性影响的宽波束模型，二维空域内的距离延迟误差分析定量说明了本文方法具有显著的成像处理优势。另外，针对这两种误差精确补偿运算量非常大的实际问题，文中提出了一种兼顾补偿精度和实现效率的距离向时域分块-频域补偿的多接收阵SAS波数域成像方法，并采用仿真实验和实测数据验证了文中方法的有效性和可行性。

1 多接收阵SAS成像几何

多接收阵SAS成像几何如图1所示，定义r轴为距离维，x轴为方位维，平台在以速度v沿x轴作匀速直线运动的同时，发射阵元向正侧方向发射一个与平台位置无关的线性调频信号，其复包络为

式中:rect(τ)为门函数，Tp表示信号脉冲宽度，γ为调频率，τ为距离向快变时间。

在发射信号的双程传播时间τ*［10］内，接收阵向前运动了vτ*的距离，当平台速度较大或成像距离较远时，如果不加以补偿将会导致图像模糊。文献［4，9］以波束中心为参考，进而采用统一的误差形式同时补偿波束内不同方向上目标的误差，当波束较窄时，这可以取得较好的结果，然而当波束变宽时，波束内不同位置的目标所对应的误差也将不同，也就是说系统误差具有方位向空变性，这里将采用等效相位中心与目标之间的精确距离来近似非“停-走-停”时间，即

式中:θ表示目标和声呐位置之间的视角，称之为侧视角，根据图1可以表示为

在宽波束条件下，PCA所导致的误差也具方位向空变性，根据文献［5］，可以得到随侧视角变化的PCA误差为

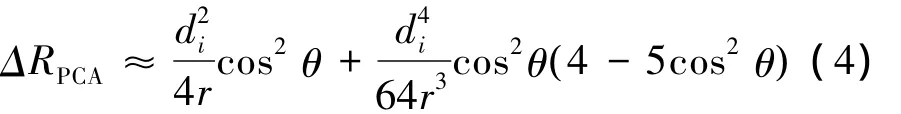
式中:di表示发射阵元与第i个接收阵元之间的距离。

图1 多接收阵SAS成像示意图Fig.1 Multi-receiver of SAS

考虑到式(2)和式(4)，将文献［4］中的近似斜距模型修正为

式中:RT( t ;r )=+ (vt)2，表示发射阵元与目标之 间 的 斜 距 历 程; RRi(t;r)=，表示考虑非“停-走-停”影响时接收阵元与目标之间的斜距历程。

于是，第i个接收阵元接收到坐标为(r，0)位置处目标的回波信号为

式中:c为水声声速;λ为对应于中心频率fc的波长;wa(t)为方位向窗函数，与滤波加权和收发阵元子系统的波束形状有关。为简化分析，在后面的讨论中，将重点讨论相位项，而忽略包络的影响。

2 误差分析

2.1 距离延迟误差分析

更准确的逼近精确时延模型的快速成像方法可以同时解决SAS图像高分辨和成像效率的问题，并且还能在一定程度上提高基于相关方法的运动误差补偿的准确性。本节将以文献［10］中精确的距离模型为标准，在二维空域内对比分析文献［4］中方法和本文方法的距离延迟误差(Δr)。

利用多接收阵SAS具有方位向空不变性和距离向空变性的性质［11］，可以将文献［4］中的一维距离延迟误差拓展到二维空域内。不失一般性，在一个完整的合成孔径中心处设置一系列距离空变的点目标，并考察收、发阵元最远间距分别为0.5 m和3 m情况下的距离延迟误差。下面分窄、宽波束2种情况分别对比分析文献［4］和文中方法所产生的误差。首先来分析窄波束情况下的误差性能，仿真参数如表1所示。

表1 窄波束情况系统参数Table 1 System parameters in narrow-beam case

在窄波束情况下，当收发阵元最远间距为0.5 m时，对应于文献［4］和文中所给出方法的距离延迟误差如图2所示;图3对应于2种方法在收发阵元最远间距为3 m时的距离延迟误差。

图2 窄波束情况下收发阵最远间距为0.5 m时的距离延迟误差Fig.2 Range propagation delay error in narrow-beam case when the distance between receiver and transmitter is 0.5 m

图3 窄波束情况下收发阵最远间距为3 m时的距离延迟误差Fig.3 Range propagation delay error in narrow-beam case when the distance between receiver and transmitter is 3 m

观察图2(a)和图3(a)可以发现，文献［4］中方法所产生的误差呈现出楔形状，这主要是由于忽略了方位向空变的非“停-走-停”误差以及合成孔径的距离向空变性所导致的;然而通过比较，文中方法可以较大程度的降低系统误差，这对成像效果的改善肯定是有一定的促进作用;即便如此，波束较窄时，系统误差方位向空变性的影响较小，是可以忽略的。

为了对比分析2种方法在宽波束情况下的误差情况，减小中心频率和收、发阵元长度以获得相对较宽的波束，具体的参数如表2所示。

表2 宽波束情况系统参数Table 2 System parameters in wide-beam case

在宽波束情况下，当收发阵元最远间距为0.5 m时，对应于文献［4］和文中所给出方法的距离延迟误差如图4所示;图5给出了2种方法在收发阵元最远间距为3 m时候的距离延迟误差。

图4 宽波束情况下收发阵最远间距为0.5 m时的距离延迟误差Fig.4 Range propagation delay error in wide-beam case when the distance between receiver and transmitter is 0.5 m.

从图4和图5中可以看到:当波束较宽时，文献［4］方法系统误差已经受到了方位向空变性的影响，而本文方法通过侧视角将系统误差的方位向空变性联系了起来，从而具有较好的精确时延模型逼近度。

图5 宽波束情况下收发阵最远间距为3 m时的距离延迟误差Fig.5 Range propagation delay error in wide-beam case when the distance between receiver and transmitter is 3 m.

2.2 微距离徙动误差分析

式(5)最后一项是非“停-走-停”和相位中心近似所产生的误差项，除了影响多普勒相位外，还将引起距离徙动，称为微距离徙动量，这里将其重写为

由式(7)可看出这个微距离徙动量是收发阵间距di的增函数，因而将随着di的增大而增大。

另一方面，求解式(7)关于r的偏导数，并求解下式

可得到满足微距离徙动量随距离增大的条件，即

由式(9)可知，在收、发阵元间距di较小时，微距离徙动量将随距离递增;然而当收、发阵元间距增大时，随距离递增的距离拐点必将会逐渐增大。

在窄波束情况下，对应于表1所示系统参数的微距离徙动误差如图6所示，图6中时延误差单位ρr表示距离分辨率。

针对于表2所示的宽波束情况，图7给出了其在距离-多普勒域内的微距离徙动误差。

图6 窄波束情况下微距离徙动误差Fig.6 Micro range migration error in narrow-beam case

图7 宽波束情况下微距离徙动误差Fig.7 Micro range migration error in wide-beam case

从图6和图7可以看到:微距离徙动量随多普勒频率和距离的不同而变化;当收发阵元间距较小时，微距离徙动量随距离递增;随着收发阵元间距的增大，距离拐点也逐渐增大，当收发阵元距离较大时，这个距离拐点超过了最大测绘距离300 m，从而成为距离的递减函数，这些结论与式(8)的理论分析是一致的。

另外，图6和图7还说明了无论波束的宽、窄，微距离徙动校正(MRCMC)都是多接收阵SAS成像预处理过程中必不可少的一个重要环节。

3 波数域成像算法

波数域成像算法又被称为ω-k成像算法［11-13］，其处理过程是先将信号变换到波数域，然后通过一致聚焦处理实现参考距离处目标的精确聚焦，最后利用Stolt变换完成非参考距离处目标的距离徙动校正和方位向精确聚焦。然而不同于收发合置SAS的信号处理，多接收阵SAS必须先进行数据预处理，将多接收阵回波信号转换成收发合置模型下的数据后才能进行成像处理。

利用相位驻留原理，可以得到与式(6)相对应的二维频域系统函数为

观察式(10)，在运用经典的收发合置SAS成像算法之前，需要先补偿与收发阵元间距有关的相位项，进而将多接收阵SAS下的二维频域系统函数补偿为收发合置SAS模型下的系统函数。下面将详细介绍预处理的具体步骤。

1)距离向脉压，其对应的相位函数为

2)补偿多普勒相位项。方位向频域变换后，在距离-多普勒域补偿多普勒相位项，其相位补偿函数为

3)微距离徙动校正。微距离徙动主要是由非“停-走-停”和相位中心近似所产生的，如果不加以补偿将会使得系统旁瓣升高，图像几何失真和对比度下降。实际上，可以通过距离-多普勒域的插值来实现微距离徙动的精确校正，然而运算量却是非常巨大的。这里采用一种同时兼顾运算量和补偿精度的称之为距离向时域分块-频域补偿微距离徙动的方法。其思路是近似认为每一个距离向时域分块数据具有相同的微距离徙动，从而对这一块数据采用相同的相位函数在频域通过相乘的方式来实现时延操作。其相乘函数为

式中:rn_ref表示第n块数据中的参考距离。

在距离向频域完成微距离徙动校正后，再在距离向时域取出对应的数据块进行重组，即可得到微距离徙动校正后的数据。

4)收发分置相位项的补偿。在距离-多普勒域补偿收发分置相位项，其相位函数为

图8给出了每个接收阵元数据的预处理操作流程。对于每个接收阵元的原始回波都要作图8所示的预处理操作，然后再将所有接收阵元预处理后的数据在距离-多普勒域进行融合，这样多接收阵SAS信号便转化为传统收发合置SAS数据模型。接下来，可以将这个融合后的数据作为传统收发合置SAS成像算法的输入进行成像处理。这里不再赘述RMA算法过程，需要注意的是，数据在Stolt插值之后作方位向IFFT之前，必须进行方位向目标走动校正，这是非“停-走-停”模型下所特有的步骤，其相位函数为

图8 第i个接收阵元回波预处理流程Fig.8 Block diagram of the preprocessing for theithre ceiver echoed data

4 仿真实验和实测数据测试

4.1 仿真实验

对于发射阵元的每个发射脉冲，接收阵元接收到的数据对应的是整个波束内所有散射点的回波。如果仅从这个实际情况出发，那么成像算法预处理中需要考虑到波束内不同目标具有不同的系统误差，也就是说系统误差具有方位空变性。实际上，如果令侧视角为零，那么文中的宽波束模型便蜕化为文献［4］中的窄波束假设，由此可见窄波束假设是一种近似处理，仅是文中宽波束模型的一个特例而已。本节将针对2.1节表1、2所示的窄波束、宽波束系统分别进行仿真研究，以验证文中方法的有效性。

首先研究窄波束情况(系统参数对应于表1)下文献［4］中方法和文中方法的成像性能。在近距离和远距离处分别设置坐标为(102 m，6 m)和(280m，50m)的理想点目标。图9为目标成像后的方位向剖面图。

图9 窄波束情况点目标方位向剖面图Fig.9 Azimuth slices for a point target in narrow-beam case

从图9中可以看到:相对文献［4］方法，文中方法还是具有一定的改善效果，但是考虑到系统误差方位向空变性的影响比较小，因而在实际中可以忽略方位向空变性的影响。对比图9文中方法微距离徙动校正前后的成像结果，可以看到微距离徙动校正确实是多接收阵SAS成像中必不可少的步骤。

获得文中方法在窄波束情况下的聚焦性能后，再来研究文中方法在宽波束情况下的成像性能。同样在近距离和远距离处分别设置坐标为(102 m，18 m)和(280 m，75 m)的理想点目标。目标聚焦后的方位向剖面图如图10所示。

对比图10成像结果，可以明显看到文中方法在宽波束条件下成像处理的优势。同时也说明了宽波束情况下微距离徙动校正的必要性，吻合于2.2节的结论。观察图10(d)，文献［4］的方法使目标存在一个较小的偏移，另外其主瓣已经存在一定程度的畸变，而本文方法成像结果基本没有任何畸变。

图10 宽波束情况点目标方位向剖面图Fig.10 Azimuth slices for a point target in wide-beam case

4.2 实测数据测试

本小节主要采用2010年7月ChinSAS-150产品在浙江淳安千岛湖试验中的某航次实测数据进一步验证文中所提出方法的正确性，其试验参数为:发射信号中心频率为150 kHz，信号带宽为20 kHz，信号脉宽为20ms，脉冲重复时间为0.32 s;接收阵元方位向实孔径长度为0.04m，参与成像的接收阵元个数为40个，发射阵元方位向实孔径为0.08m，声呐载体速度为2.5m/s。

图11 实测数据成像结果Fig.11 Imaging results of real data

试验场景为千岛湖湖底地形地貌，在数据处理前，先完成各接收阵数据的两两叠加处理，即1+2，2+3，…。成像结果如图11所示，其中图11(a)为文献［4］方法处理后的成像结果，图11(b)为本文方法处理后的成像结果。对比两图可以发现:沿方位向，图11(b)在两端边缘10 m的范围内具有更加清晰的重构场景。另外，需要说明的是该系统所对应的波束较窄，与表1所示参数相当;因此文中方法的优势还有待于下一代高分辨SAS系统的进一步验证。

5 结束语

窄波束假设的处理前提是系统误差相对波束内任何方位位置的目标均近似相同，即不考虑系统误差的方位空变性。文中根据方位向侧视角和多普勒瞬时频率之间的一一映射关系，建立的宽波束模型兼容窄波束假设处理方法，很好地解决了系统误差的方位空变性问题。

文中针对宽波束模型下的微距离徙动校正耗时量较大的问题，提出了一种距离向时域分块-频域补偿的多接收阵SAS成像处理方法。该方法同时兼顾了补偿精度和实现效率，利用二维误差分析和仿真实验来验证文中方法的优势，并采用实测数据来检验文中方法的可行性;然而其优势还有待于实验数据的进一步测试。

［1］孙大军，田坦.合成孔径声呐技术研究［J］.哈尔滨工程大学学报，2000，21(1):51-56.SUN Dajun，TIAN Tan.The study of synthetic aperture sonar(SAS)technique［J］.Journal of Harbin Engineering University，2000，21(1):51-56.

［2］HAYESM P，GOUGH P T.Synthetic aperture sonar:a review of current status［J］.IEEE Journal of Oceanic Engineering，2009，34(3):207-224.

［3］SOUMEKH M.Synthetic aperture radar signal processing with matlab algorithm［M］.New York:Wiley，1999:56-57.

［4］杨海亮，张森，唐劲松.宽测绘带多接收阵合成孔径声呐成像处理方法［J］.系统仿真学报，2011，23(7):1424-1428.YANG Hailiang，ZHANG Sen，TANG Jinsong.Study on simulation of multiple-receiver synthetic aperture sonar imagery based on wide swath［J］.Journal of System Simulation，2011，23(7):1424-1428.

［5］BELLETTINIA，PINTO M A.Theoretical accuracy of synthetic aperture sonar micronavigation using a displaced phase-center antenna［J］.IEEE Journal of Oceanic Engineering，2002，27(4):780-789.

［6］YAMAGUCHI I.A technique of multi-aperture transmitting receivering on synthetic aperture sonar［J］.Electronics and Communications in Japan，1999，82(3):66-73.

［7］BONIFANTW W.Interferometric synthetic aperture sonar processing［D］.Atlanta:Georgia Institute of Technology，1999:38-42.

［8］CALLOW H J.Signal processing for synthetic aperture sonar image enhancement［D］.Chrirstchurch:University of Canterbury，2003:64-68.

［9］汪海涛，唐劲松，苑秉成.多子阵SAS逐线成像算法研究［J］.哈尔滨工程大学学报，2009，30(7):820-823.WANG Haitao，TANG Jinsong，YUAN Bingcheng.Research on a multi-receiver synthetic aperture sonar imaging algorithm based on FFT［J］.Journal of Harbin Engineering University，2009，30(7):820-823.

［10］唐劲松，张春华，李启虎.多子阵合成孔径声呐逐点成像算法［C］//中国科学院声学研究所1999年青年学术交流会.北京，中国，1999:235-239.

［11］BAMLER R.A comparison of range-Doppler and wavenumber domain SAR focusing algorithms［J］.IEEE Transactions on Geoscience and Remote Sensing，1992，30(4):706-713.

［12］PRATIC，ROCCA F，GUAMIERIA M.Seismic migration for SAR focusing:interferometrical application ［J］.IEEE Transactions on Geoscience and Remote Sensing，1990，28(4):627-639.

［13］REIGBER A，ALIVIZATOSE，POTSISA，et al.Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation ［J］.IET Radar，Sonar and Navigation，2006，153(3):301-310.