基于二阶差分滤波器的水下目标纯方位角跟踪

王宏健，徐金龙，么洪飞，2，张爱华

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001;2.齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔161006)

水下目标跟踪包括基于多声呐的目标跟踪和基于单声呐的目标跟踪2种方式。其中，水下目标纯方位角跟踪(bearing-only tracking，BOT)是基于单声呐目标跟踪的重要方法。BOT是通过被动声呐平台的水听器阵列获得的一系列方位角测量数据序列来估计目标运动参数的技术［1］。

在BOT定位跟踪中，滤波算法是核心技术。目前，BOT跟踪系统中应用通常采用改进的卡尔曼滤波算法，包括扩展卡尔曼滤波(extended Kalman filter，EKF)［2-3］及无迹卡尔曼滤波算法 (unscented Kalman filter，UKF)［4-5］等。EKF 算法的性能依赖于系统的局部非线性强度，UKF算法原理主要是通过构造一组加权样本点来逼近待估计参数，避免EKF算法线性化的缺点，是一种可以直接应用于非线性系统状态估计的滤波方法。但UKF算法同样由于噪声信号及计算误差等因素而容易导致误差协方差矩阵负定，从而使得滤波结果发散。

本文在EKF算法的基础上，提出了基于二阶差分滤波器(second-order divided difference filter，DDF2)的BOT算法。该算法在BOT跟踪系统线性化时采用Stirling插值法，避免了因计算Jacobian矩阵或Hessian矩阵而导致计算的负担，同时也放宽了跟踪系统的状态方程必须满足可微性的约束。

2005年，Lee［6］提出了 DDF 滤波方法。文献［7-8］在弹道导弹跟踪问题中应用了DDF1、DDF2并与EKF、UKF方法进行了状态估计性能对比。文献［9-10］提出了一种基于数据融合算法的DDF2，并且应用于刚体的姿态角估计中。文献［11］将DDF1、DDF2应用于月球车的运动状态参数估计中。文献［12］将DDF1、DDF2应用于全球位置导航系统，并且得出了DDF1、DDF2的估计精度要明显高于EKF。

本文将DDF2引入到对水下目标的纯方位角跟踪问题中，并用与DDF1及传统的EKF方法进行仿真对比分析，结果表明DDF2及DDF1算法的滤波精度要明显优于 EKF，且由于 DDF2采用二阶Stirling插值法线性化BOT跟踪系统模型中的非线性项，DDF2算法的滤波精度要高于 DDF1，而且DDF2的滤波稳定性要优于另外2种方法。

1 问题描述

在BOT问题研究中，被动声呐平台和水下目标可以被看作空间中的2个质点，本文假设目标的加速度变化满足高斯随机过程［13］。

1.1 水下目标的运动学模型

由于通常水下目标相对于被动声呐平台距离很远，可以不考虑水下目标在垂直于地面方向上的距离的变化。因此为了使问题简化，本文仅考虑二维平面中对匀速直线运动的水下目标跟踪问题。在水平面直角坐标系中，目标在X-Y上的位置坐标为(xt，yt)，各方向的速度记为()，如图1所示。将目标的状态向量定义为

被动声呐平台的状态向量定义为:

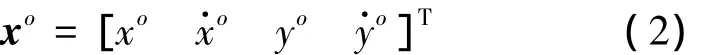
式中:(xo，yo)及)分别为被动声呐平台的位置和速度。这样目标与平台的相对运动状态向量可以表示为

若假设目标作匀速直线运动，根据文献［14］，水下目标与被动声呐平台的相对运动状态方程为

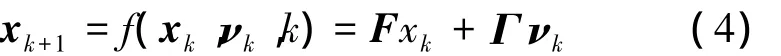
式中:F、Γ为状态转移矩阵，如式(5)、(6)所示;T为采样周期;νk为过程噪声且满足形如 νk～N(ν-，Qk)的高斯分布;Qk=σaI2，σa为标量，I2为2×2单位矩阵。

被动声呐平台与水下目标相对运动情况如图1所示，图中ψt表示水下目标的航向，Vt表示水下目标的运动速度，Vo表示被动声呐平台的运动速度，(r0…rk)为目标与被动声呐平台的相对距离序列。

图1 平台与目标运动的几何关系Fig.1 Geometric relationship between platform and target

1.2 被动声呐测量模型

由于本文仅考虑被动声呐平台通过对水下目标与平台相对方位角信息的观测来完成目标跟踪。因此，第k时刻被动声呐平台的测量模型可以表示为

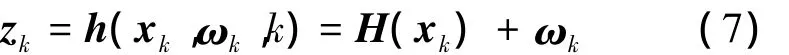
式中:H(xk)为被动声呐测得的方位角，如式(8)所示;ωk为测量噪声，且满足形如ωk～ N(ω-k，Rk)的高斯分布。

目标跟踪系统的数学模型由方程由式(4)、(7)组成。目标跟踪算法便能够通过给定的方位角测量序列Zk={zi}来估计状态向量xk。由于被动声呐的测量模型是关于状态向量的非线性函数，因此，BOT目标跟踪属于典型的非线性滤波估计。文献［15-16］指出，被动声呐平台必须做适当的机动策略才能完成对目标的跟踪。

2 基于DDF2的BOT算法

本文将利用二阶Stirling插值公式的多变量扩展形式来近似处理被动声呐的测量模型中非线性项，进行二阶截断，并且DDF2采用与EKF算法相同的预测-校正结构［17］，以得到被动声呐测量的预测值及新息的协方差矩阵，修正目标状态的估计值，实现纯方位角跟踪。

首先定义协方差矩阵的Cholesky分解［18］:

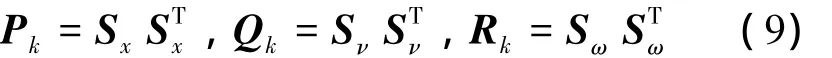
DDF2滤波器计算状态预测向量x^-k+1的计算方法为

式中:h为插值步长，nx=4及nν=2分别为状态向量的维数及噪声向量的维数，Sx，p为矩阵Sx的第p列向量，Sν，p为矩阵Sv的第p列向量。

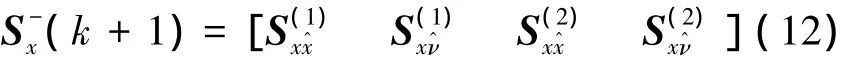
式中:

式中:Sx，j为矩阵 Sx的第 j列向量，Sν，j为矩阵 Sv的第 j列向量;i，j=1，2…4。

式中:nω=2为噪声向量的维数，为矩阵的第p列向量，Sω，P为矩阵Sω的第p列向量。观测协方差矩阵如下:

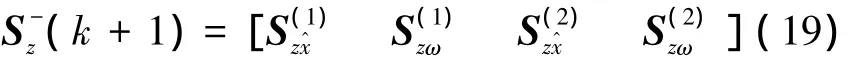
式中:

滤波器增益 κk+1，状态估计向量及状态估计协方差矩阵如下:

以上给出了基于DDF2算法的BOT跟踪算法的详细推导过程，在此基础上给出该算法的流程图，如图2所示。

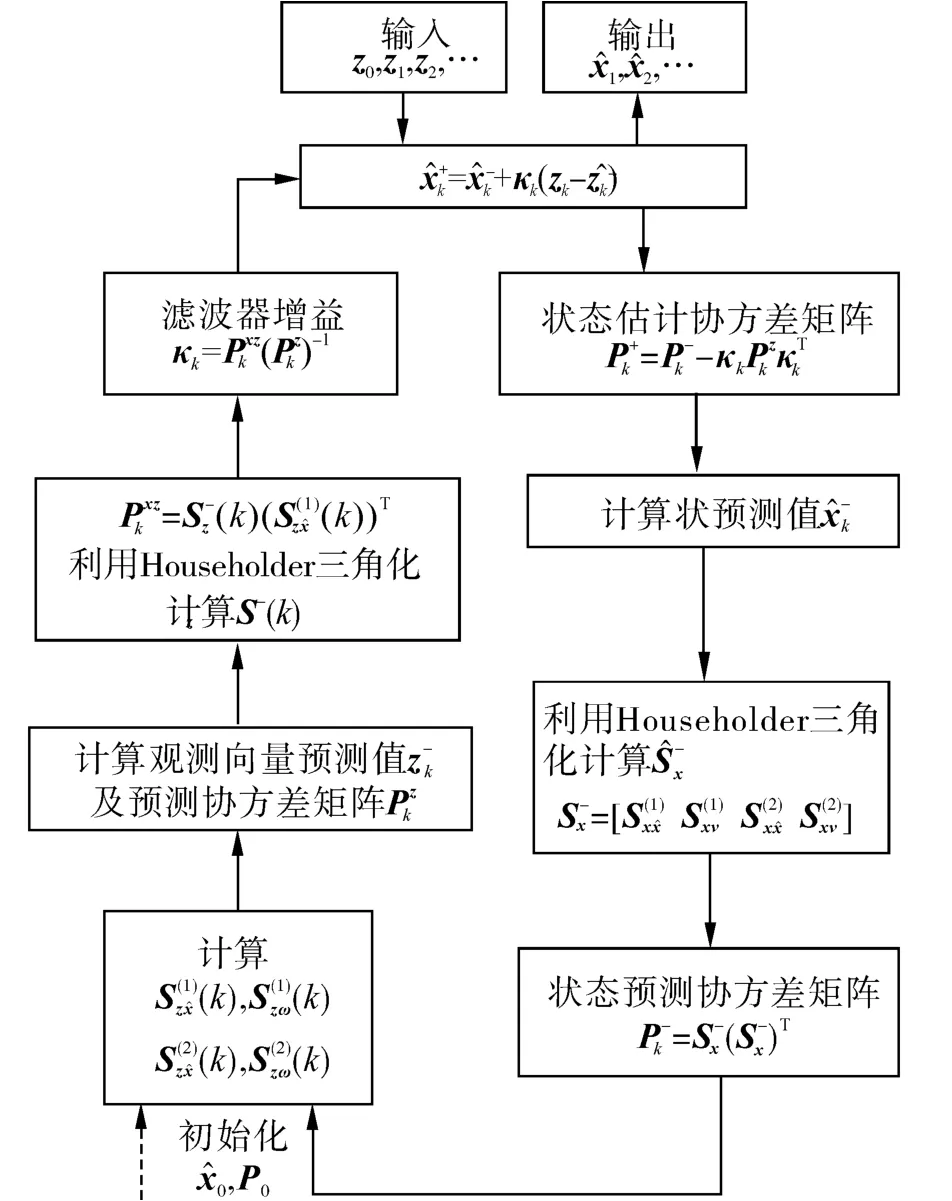
图2 DDF2算法流程图Fig.2 Block diagram of DDF2

3 仿真分析

3.1 Monte Carlo仿真

仿真案例为被动声呐平台跟踪某匀速直线运动的水下目标，设定仿真时间为1 000 s，仿真步长T=1 s。假定被动声呐平台在跟踪水下目标的过程中做360°转向机动。水下目标及被动声呐平台的运动状态初始值设定如表1所示。

在设定滤波器的初始状态时，假设初始时刻水下目标和被动声呐平台的相对距离r0为已知，而水下目标的运动速度未知，初始时刻通过被动声呐测得水下目标的方位角为 z0。令M=，则滤波器的初始状态x0及初始协方差矩阵P0表示为

表1 水下目标及被动声呐平台的运动状态设置Table 1 Target and passive sonar platform motion state set

在上述初始条件下，分别将本文所提出的基于DDF2的BOT目标跟踪算法与前面所提及的DDF1和EKF算法进行100次Monte Carlo仿真实验。通过这3种方法对水下目标的位置、速度、航向进行滤波估计，并估计出平台和水下目标的相对距离，仿真结果如图3所示。

由图3可以看出，在相同的初始条件下，若被动声呐平台也做相同的机动，本文所提出的方法能够快速跟踪到目标的位置、速度等真值。从图3(b)可以看出，虽然DDF1及EKF能够快速的对目标的速度进行状态估计响应，但是其不能收敛到目标真值，而DDF2则能收敛到目标真值，说明DDF2的跟踪能力要明显强于DDF1及EKF，而DDF1的跟踪能力也要强于EKF。

图3 目标的位置、速度、距离及艏向跟踪Fig.3 Position，velocity，distance and course tracking

同时也能够看到，在初始的一段时间里，这3种方法对水下目标的跟踪都出现了一个较大的偏差，这主要是由目标的初始速度未知所导致的。

3.2 均方差统计特性

为了深入的对比和分析本文所提出的方法和基于DDF1及EKF算法的性能，通过状态的均方根误差(RMSE)统计特性来有效的表征这3种方法的状态估计精度。经过100次Monte Carlo仿真试验得到的位置及速度的RMSE统计特性如图4所示。在相同的仿真条件下，DDF2具有更高的估计精度，而EKF的估计精度最低。

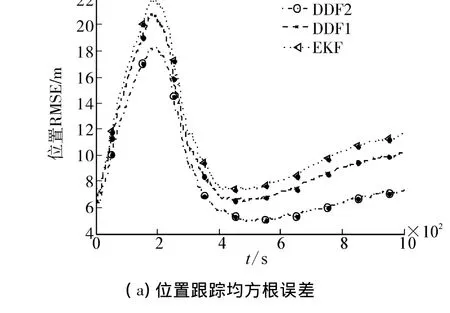
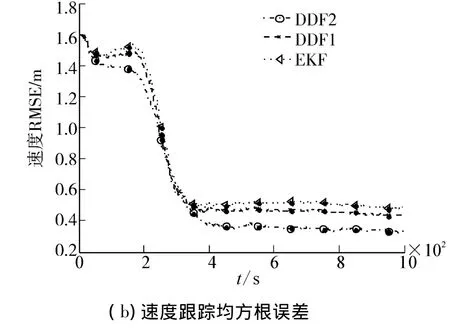
图4 位置及速度跟踪均方根误差Fig.4 RMSE of position and velocity tracking

4 结束语

本文所提算法可以避免传统EKF利用Taylor级数展开进行线性化以及需要计算Jacobian矩阵而导致的计算过程复杂和难以进行实际应用的问题，且具有比DDF1更高的跟踪精度。该方法不仅简化了目标跟踪的计算过程，而且具有良好跟踪精度。最后，为了验证本文所提出的算法的性能，通过Monte Carlo方法进行了100次仿真试验，并将本文提出的方法与DDF1及EKF方法进行了对比分析。

仿真结果表明:在相同初始条件下，基于DDF2的目标跟踪算法具有更快速准确的跟踪响应。此外，通过RMSE统计方法得到的仿真结果也验证了这种方法具有较高的估计精度。

［1］AIDALA V J，HAMMEL S.Utilization of polar coordinates for bearings-only tracking［J］.IEEE Transactions on Automatic Control，1983，28(2):283-294.

［2］MURPHY D J.Noise bearings-only target motion analysis［D］.Kirkland:Northwestern University，1970:151-157.

［3］岳剑平，梁国龙，王燕.水下动目标纯方位被动跟踪仿真研究［J］.哈尔滨工程大学学报，2003，24(5):500-504.YUE Jianping，LIANG Guolong，WANG Yan.Simulation study on passive tracking of underwater moving target for bearing only［J］.Journal of Harbin Engineering University，2003，24(5):500-504.

［4］曲毅，刘忠.基于UKF的水下目标纯方位跟踪算法［J］.舰船科学技术，2009，31(7):133-136.QU Yi，LIU Zhong.Research of underwater bearings-only target tracking algorithm based on UKF［J］.Ship Science and Technology，2009，31(7):133-136.

［5］吴盘龙，孔建寿.基于平方根UKF的水下纯方位目标跟踪［J］.南京理工大学学报:自然科学版，2009，33(6):751-755.WU Panlong，KONG Jianshou.Underwater bearing-only target tracking based on square-root UKF［J］.Journal of Nanjing University of Science and Technology:Natural Science，2009，33(6):751-755.

［6］LEE D J.Nonlinear Bayesian filtering with applications to estimation and navigation［D］.Texas:Texas A＆M University，2005:134-139.

［7］SAULSON B G，CHANG K.Nonlinear estimation comparision for ballistic missile tracking［J］.Optical Engineering，2004，43(6):1424-1438.

［8］WU C，HAN C.Second-order divided difference filter with application to ballistic target tracking［C］//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing，China，2008:6342-6347.

［9］SETOODEH P，KAYTIAIN A，FARJAH E.Attitude estimation by divided difference filter-based sensor fusion［J］.The Journal of Navigation，2007，60(1):119-128.

［10］AHMADIM，KHAYATIAN A，KARIMAGHAEE P.Attitude estimation by divided difference filter in quaternion space［J］.Acta Astronautica，2012，75:95-107.

［11］BHALE P G，DWIVEDIP N，KUMAR P.Estimation of ballistic coefficient of reentry vehicle with divided difference filtering using noisy RF seeker data［C］//Proceedings of the IEEE International Conference on Industrial Technology.Mumbai，USA，2006:1087-1092.

［12］JWO D J，HSIEH M Y，LAI S Y.GPS navigation processing using the quaternion-based divided difference filter［J］.GPSSolut，2010，14:217-228.

［13］徐卫明，刘雁春，殷晓东.基于交互多模型的水下目标跟踪方法［J］.武汉大学学报:信息科学版，2007，32(9):782-785.XU Weiming，LIU Yanchun，YIN Xiaodong.Underwater target tracking based on interacting multiple model method［J］.Geomatics and Information Science of Wuhan University，2007，32(9):782-785.

［14］FRIENDLAND B.Optimum steady-state position and velocity estimation using noisy sampled position data［J］.IEEE Transactions on Aerospace and Electronic Systems，1973，9(6):906-911.

［15］ARULAMPALAM M S.RISTIC B，GORDON N.Bearings-only tracking of manoeuvring targets using particle filters［J］.EURASIP Journal on Applied Signal Processing，2004，2004(15):2351-2365.

［16］KIRUBARAJAN T，BAR-SHALOM Y，LERRO D.Bearing only tracking of manoeuvring targets using a batch-recursive estimator［J］.IEEE Transactions on Aerospace and Electronic Systems，2001，37(3):359-368.

［17］NORGAARD M，POULSEN N，RAVN O.New developments in state estimation for nonlinear systems［J］.Automatica，2000，36:1627-1638.

［18］张贤达.矩阵分析与应用［M］.北京:清华大学出版社，2009:347-360.