动态部署与分块存储策略的数据恢复模型

黄春梅，姜春茂，曲明成

(1.哈尔滨师范大学计算机科学与信息工程学院，黑龙江哈尔滨150025;2.哈尔滨工业大学计算机科学与技术学院，黑龙江哈尔滨150001)

随着云计算和大数据计算的飞速发展，以及网络传输速度快速提升和无线通信(3G4G)技术广泛应用，为数据的网络存储带来了新的契机。为了增加数据存储的可靠性和易用性，学术界涌现出很多的研究成果［1-3］。研究方向主要分成2类，基于编码解码的分布式存储，和基于冗余块的分布式存储。基于编码的策略主要源于通信领域，其核心思想是将原始数据等分为m块，进而融合一定冗余编码成n块，n＞m，当存在x个节点失效时(x＜n-m)，可以从其余节点恢复出原始数据。而基于冗余块的分布式存储，出现了2个研究方向，完全多副本存储和分块冗余存储。前者将完整的副本数据直接存储网络节点，并多不考虑动态部署过程，根据数据存储可靠性和节点的可靠性采用静态初始发布机制来确定最终数据的可靠性［6-8］。但是随着信息技术的飞速发展，对数据存储提出了更高的要求，如何在现有网络和节点环境下进一步大夫提升数据的可靠性是一个亟待解决的重要问题。融合动态数据恢复技术的Google公司的GFS系统和Apache基金会的Hadoop系统，采用了分块分布式冗余存储策略，在数据存储节点发生故障时，通过其他节点存储的冗余数据，将故障节点数据快速重新部署到新的节点，以保证数据整体的可靠性［9-10］。

综上，编码策略、分块冗余存储与动态部署技术对于数据高可靠存储管理具有较大的优势，但是目前能够将三者融合考虑的相关研究较少，并且采用这种数据存储管理机制，数据的可靠性可以达到何种程度是一个关键性问题，而在当前的研究中很少有研究成果评估这种机制对数据可靠性的影响，缺乏一个有效的评估方法或评估模型。

基于上述理论和存在的问题，本文基于分块存储［5，11］、编码策略、动态恢复提出了多个动态数据恢复模型(数据失效概率模型)。采用指数分布函数来刻画存储节点的可靠性，通过模拟正常和异常网络情况，分析了数据可靠性模型的数据可靠性，结果显示，本文提出的模型在已知网络存储环境的前提下能有效度量数据的可靠性，给出较好的评估，并且较直接分块存储和编码解码策略对数据的可靠性有很大的提升，并进一步对可靠性模型的影响因子进行了分析，从而增强了可靠性模型的实用性和易用性。

1 基本原理

在可靠性设计中常用分布函数有:二项分布、泊松分布、指数分布、正态分布、对数正态分布和韦布尔分布。而对处于稳定工作状态的电子机械或电子系统的失效概率基本上服从指数分布。

定义1 可靠度(reliability)也叫可靠性，指的是产品在规定的时间内，在规定的条件下，完成预定功能的能力，它包括结构的安全性，适用性和耐久性，当以概率来度量时，称可靠度。

对产品而言，可靠度越高就越好。可靠度高则可以更长时间的正常使用，消费者或许希望看到这点(其中也有质量成本问题);从专业名词的角度来说，可靠度越高的产品，意味着产品正常工作无故障的时间就越长。

1)指数分布可靠度

当失效率为常数时，即:λ(t)=λ时则有

2)指数分布失效概率密度函数

其分布均值和方差分别为

通过对密度函数积分可以求出节点在确定时间点的失效概率函数:

3)指数分布曲线

指数分布概率密度函数、节点失效概率、节点可靠度分布曲线分别如图1中的(a)、(b)和(c)所示。

4)一段时间的平均失效概率:

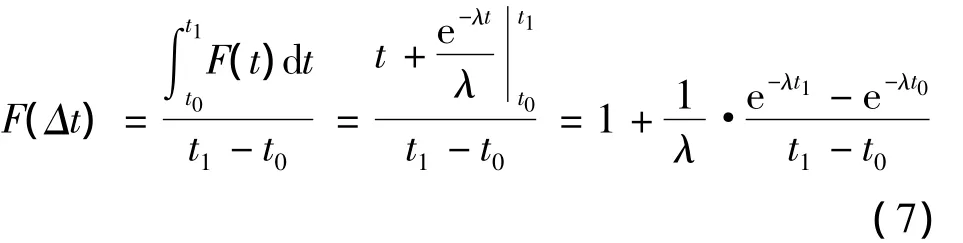
为了简化计算过程，令从时间节点0开始计时，则由式(7)可以化简推出:

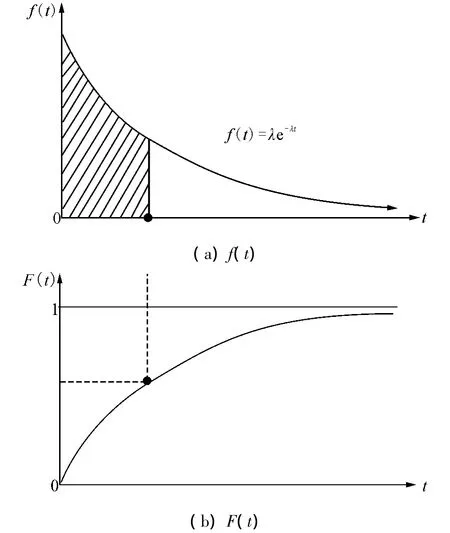
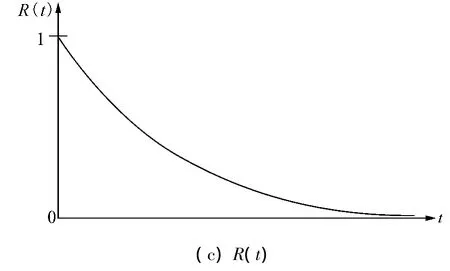
图1 指数分布曲线Fig.1 Exponential distribution curve

5)基于动态恢复技术的数据失效概率。

从动态部署技术的过程可以看出，如果采用冗余结构存储数据，当节点发生失效时，需要根据其他节点快速部署失效节点存储的数据。

定义2 数据失效概率f将当前可用的存储了同一数据的所有节点的数据作并集处理，如果得到的数据是不完整的，则称发生了数据失效，发生的概率为f。

比如有3个节点，节点N1、N2存储相同的数据data1，当检测到N1发生失效时，需要从N2向N3重新部署数据data1，以保证同时有2个节点存储了data1。

2 基本存储与可靠性模型

2.1 完全双副本存储

传统的双副本存储过程是，对于一个大小为M的数据D，将其完整副本分别存储2台服务器上形成2个完整的拷贝，如图2。

显然这种存储方式占用的存储空间大小为2M。

基于双副本和动态部署技术，在一个节点发生失效时，选取一个新的节点恢复数据，令从一个节点恢复数据量M所需要的时间长度为Δt。

图2 完整双副本存储Fig.2 The complete double copy storage

那么在Δt时间内，如果2个节点都失效，则发生数据失效。根据式(8)，得出其数据失效概率模型:

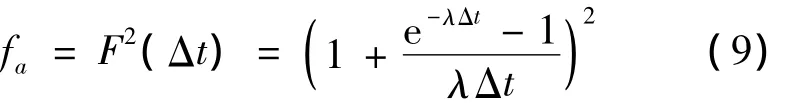
2.2 分块双副本存储

定义3 I等分双副本存储(I aliquot double copy，IADC)对于一个大小为M的数据D，将其等分成i份即D=D1+D2+… +Di，且其大小M1=M2=Mi=M/i。称这种划分和存储策略为I等分双副本存储。如图3所示。

显然I等分双副本存储占用的存储空间总量为2M。

基于I等分双副本存储和动态部署技术，需要2i个节点存储数据，peer(2i-1)与peer(2i)相当于传统的双副本存储。

每个 peer节点存储的数据量为 M/i，则如果peer(2i-1)、peer(2i)中如果有一个节点发生失效时，对于数据Di的数据失效概率为，则整体的数据失效概率fc为

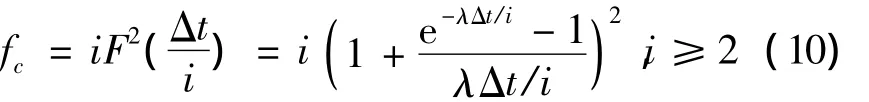
图3 I等分双副本量存储策略Fig.3 I aliquots double copy storage strategy

3 I等分和模型散列存储的可靠性模型

文献［5，11］中提出了一个存储模型，通过对原始数据进行规则划分，在i个节点上基于双倍副本量存储，当有1个节点失效失效，其他i-1个节点存储的数据仍然是完整的。基于该模型取存储节点为3。

定义4 k等分模型散列存储(Kaliquot model hash，KAMH)对于一个大小为M的数据D，将其等分成i份(i＞ =1)即M=m1+m2+…+mk，且其大小m1=m2=mk=M/i。称这种划分和存储策略为i等分模型散列存储。如图4所示。

为了使占用的存储空间为2M，可以控制散列模型中的冗余量，使占用的存储空间总量也为2M。

在这种存储策略中，每个G-peer组由y个节点构成，先令y=3。当一个G-peer中有不多于一个节点失效时，可以从其他2个节点进行动态恢复。

恢复的数据量为2M/3，恢复速度为2V。则恢复时间为Δt/3。

图4 I等分和模型散列存储原理图Fig.4 I aliquots and model hash stored schematic

单个节点在(0，Δt/3)跨度内的失效概率f为

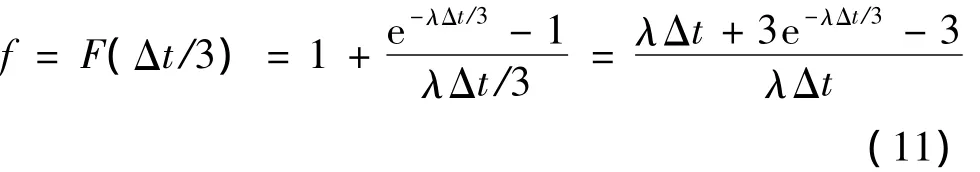
当i=1，y=3时，数据失效概率为

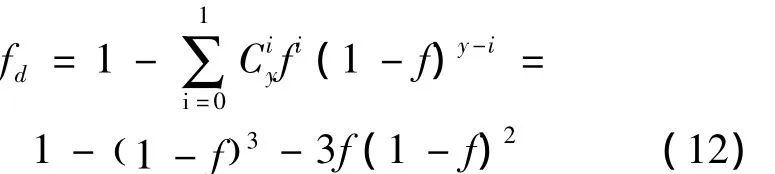
当i＞1，y=3时，数据失效概率为

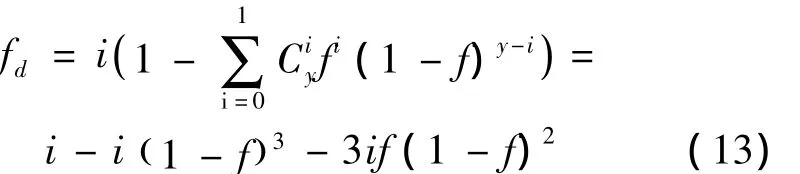
3.1 G-peer组成员为3时性能分析

1)网络传输正常时比较。令i与λΔt取不同值，记录相应fd取值，如表1所示，从中可以看出随着i的增加，fd取值逐渐降低。

表1 i与 λΔt变化时fd取值Table 1 The value of fd when i and λΔt changes

观测i=2时，fd/fc的比值，如图5所示，随着λΔt的增加，fd/fc逐渐增加，但是都小于0.5，说明fd一直优于fc。

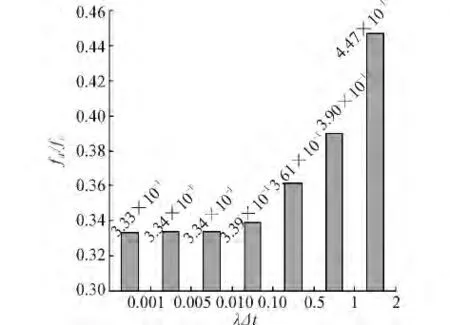
图5 k=2时λΔt与fd/fc的关系Fig.5 Relationship between λΔt and fd/fc when k=2

观测λΔt=0.001，i取不同值，fd走势。如图6所示，随着k的增加fd逐渐降低。

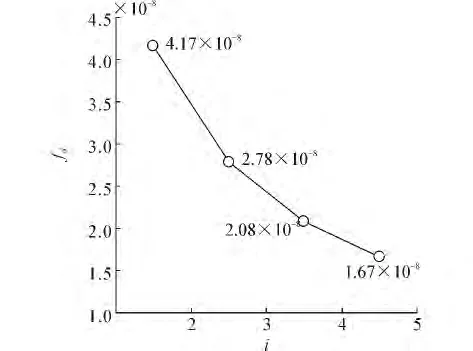
图6 λΔt=0.001时i与fd的影响Fig.6 The impact of i and fd when λΔt=0.001

2)网络传输非正常时比较。传输速度降级时的性能。检测i=2时速度降低时的性能，此时如果出现如果数据恢复，一次恢复的数据量为，则从2个点恢复数据的聚集速度位于(V，2V)。则相应的恢复时间为(Δt/6，Δt/3)。此时式(11)变为

从表2可以看出，随着x的增加，a值逐渐降低，模型性能越好。

比较fd/fc，2等分。取几组数值，形成图7，从中可以看出，当x=1.1时fd/fc＞1，除此均小于1，而且随着x的增加，逐渐降低，说明fd越优于fc。比较fd/fa，2等分。取几组数值，形成图8，从中可以看出，x取任意值时fd/fc＜1，而且随着x的增加，逐渐 降低，说明fd越优于fa。

表2 k=2时速度变化对模型的影响Table 2 Effect of velocity change on the model when k=2

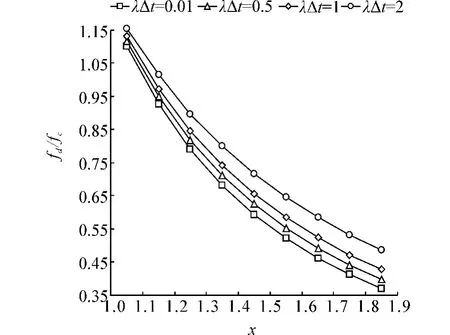
图7 i=2时速度变化对fd/fc的影响Fig.7 Effect of velocity change on fd/fc when i=2

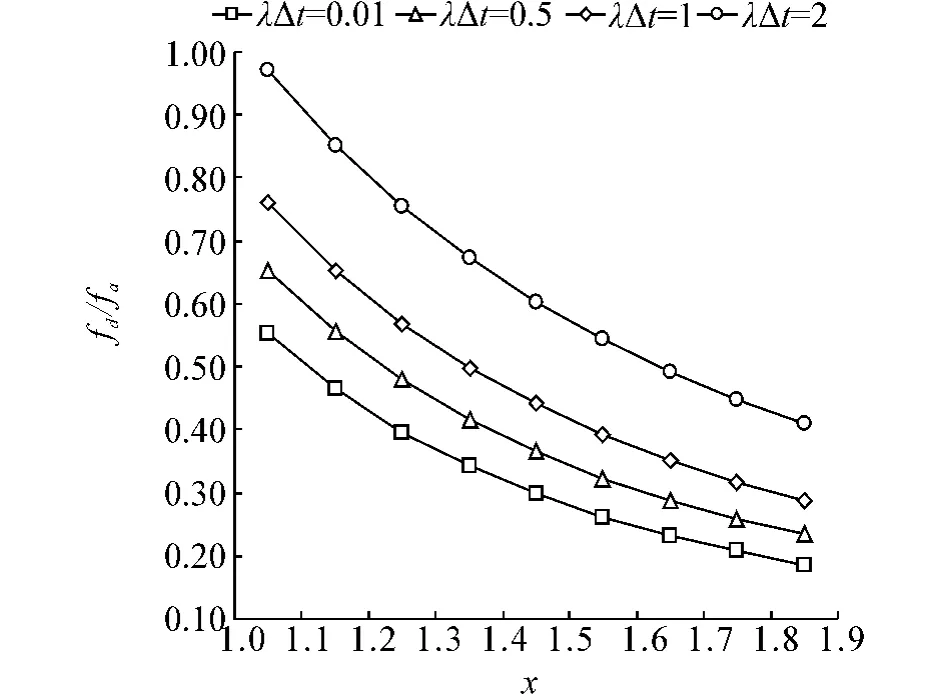
图8 i=2时速度变化对fd/fa的影响Fig.8 Effect of velocity change on fd/fa when i=2

3.2 G-peer组成员大于3时性能分析

1)速度呈比例增长时分析。

当y＞3时，式(13)变为

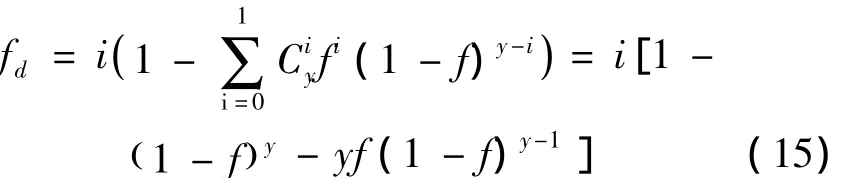
取 k=2，y=3，4，5，λΔt取不同数值，代入式(13)，结果如表3所示。可以看出在λΔt取相同数值时，y值越大fd值越小。Y取3与y取4时fd的相应比值近似为2，而y取4与y取5时fd的相应比值明显小于2，说明随着y值增加，可靠性增加变缓。

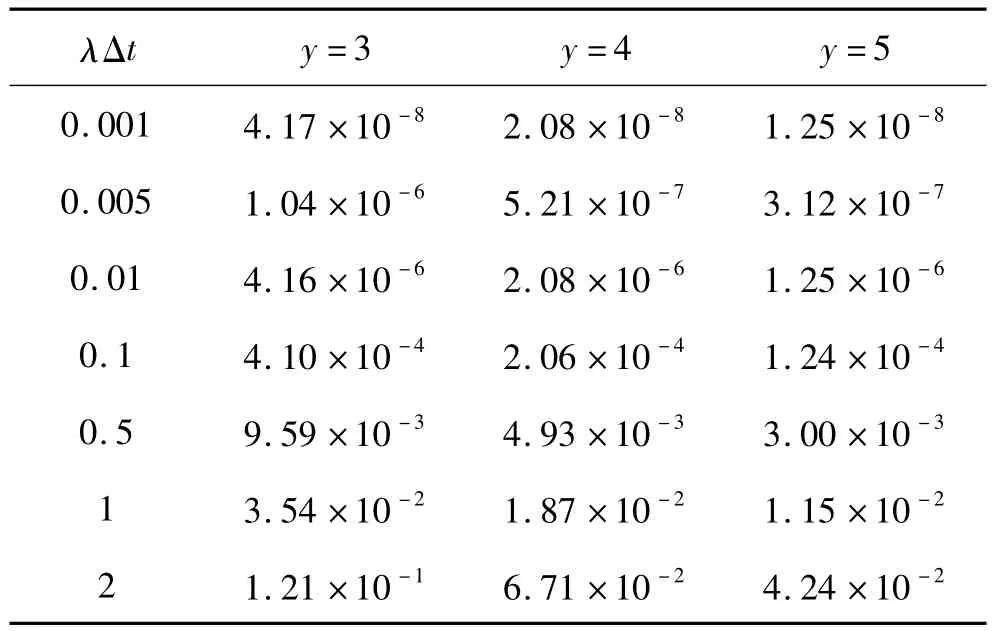
表3 k=2，y变化对模型的影响Tab le 3 The im pact of y changes on the model when k=2，

2)速度呈非线性增长时分析。

随着y的增加，动态恢复速度实际不会呈现比例增加。为了有效分析模型在这种情况下的性能，给出一个较为简洁的恢复速度增长函数如式(16)所示，b为增长系数，后面将对b={0.2，0.4}进行数值分析。如表4、5所示。

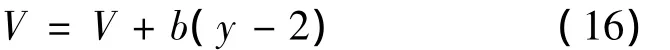
表4 b=0.2时fd取值Table 4 The value of fd when b=0.2

将表4、5形成图9，可以看出b=0.2曲线位于b=0.4曲线上方，说明fd受到影响更大，但是2条曲线都位于fc=1.25×10-7的下方，都优于fc。

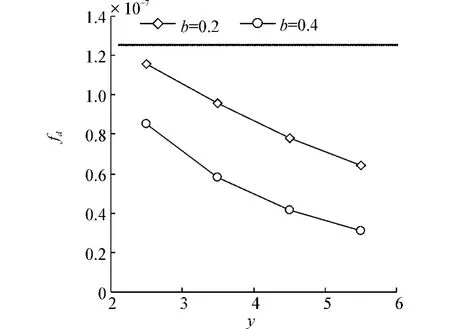
图9 k=2，y变化时fd走势Fig.9 The fd trend when k=2 and y changes

4 编码模型散列存储与可靠性模型

4.1 模型构建

定义5 编码模型散列存储对于一个大小为M的数据D，先将其等分x份(x＞1)即M=m1+m2+… +mx，且其大小m1=m2=mk=M/x。然后采用纠删码进行编码，编码无效率为ε(0＜ε＜1)，编码后块数为k(k＞x)，对k个数据块进行模型散列存储。称这种策略为编码模型散列存储。

如图10所示，从纠删码的基本原理可知，通过对原始数据M进行x等分，然后进行编码，编码无效率为ε(0＜ε＜1)，编码后块数为k(k＞x)，则只要有z=(1+ε)x个数据块存在，就可以恢复出原始数据。编码后单个数据块的数据量为Mα/x。每一个G-peer组采用y个节点对散列后的数据进行存储，则G-peer(k)组中的数据块nk失效的概率推导fg如下:

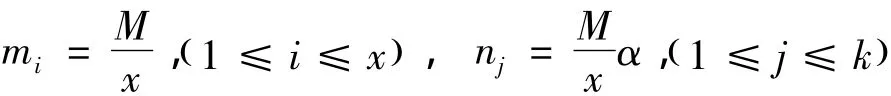
如果原来从一个节点恢复M数据时用时为Δt，编码后处理后采用3个节点模型散列Mα/x的数据，当有一个节点失效后，从2个节点恢复。恢复的时间为

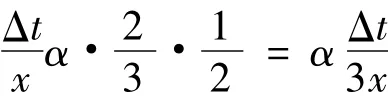
在上述恢复时间内每个节点的失效概率为

则G-peer(k)组中的数据块nk失效的概率fg:

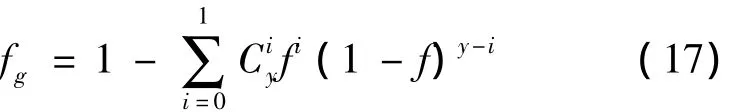
由于只要在k个数据块中获得z=(1+ε)x个数据块即可以恢复出原始数据，则数据M的失效概率fh为

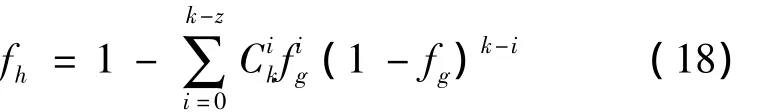
为了保证存储的总数据量不超过2M，则编码后块数k为

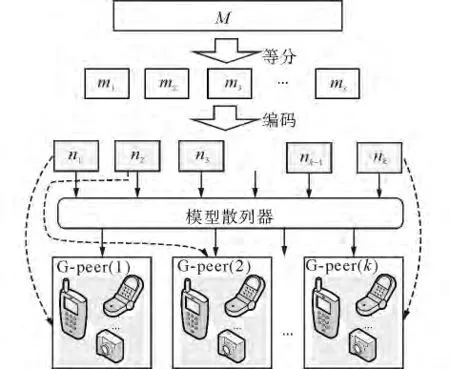
图10 编码和模型散列存储Fig.10 Coding and model hash storage

4.2 性能比较分析

根据目前纠删码相关研究，取x=10、ε=0.2、α=1.2、k==17、z=(1+ε)x=12。得出f、fg、fh的数据如表6所示。

如果直接采用纠删码存储，当有节点失效时，较难进行直接恢复，因为所有的节点都是通过完整的原始数据编码产生，如果需要恢复，则会产生较大的网络流量，且复杂度较高，时间很难保证。

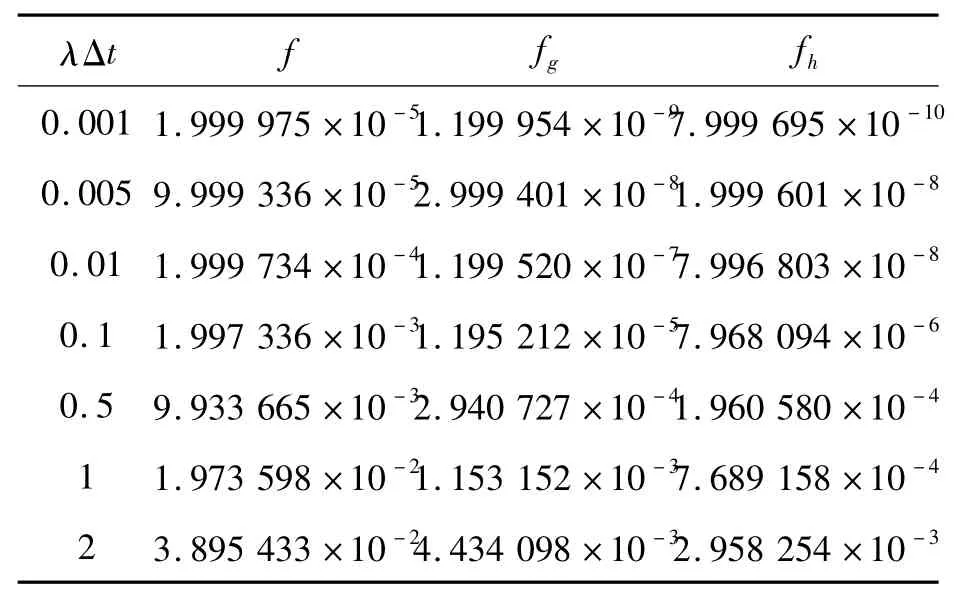
表6 x=10，ε=0.2，α=1.2时fh取值Table 6 The value of fh when x=10，ε=0.2，α =1.2

那么对于采用纠删码存储，在Δt时间内数据失效概率fj为

根据目前纠删码相关研究，取x=10、ε=0.2、α=1.2、k=「2x/α⏋=17、z=(1+ε)x=12。得到fx、fj的数据如表7所示。

表7 x=10，ε=0.2，α=1.2时 fj取值Table 7 The value of fj when x=10，ε=0.2，α =1.2

为了比较fh与fj的性能，取二者的比值为纵坐标，形成图11。

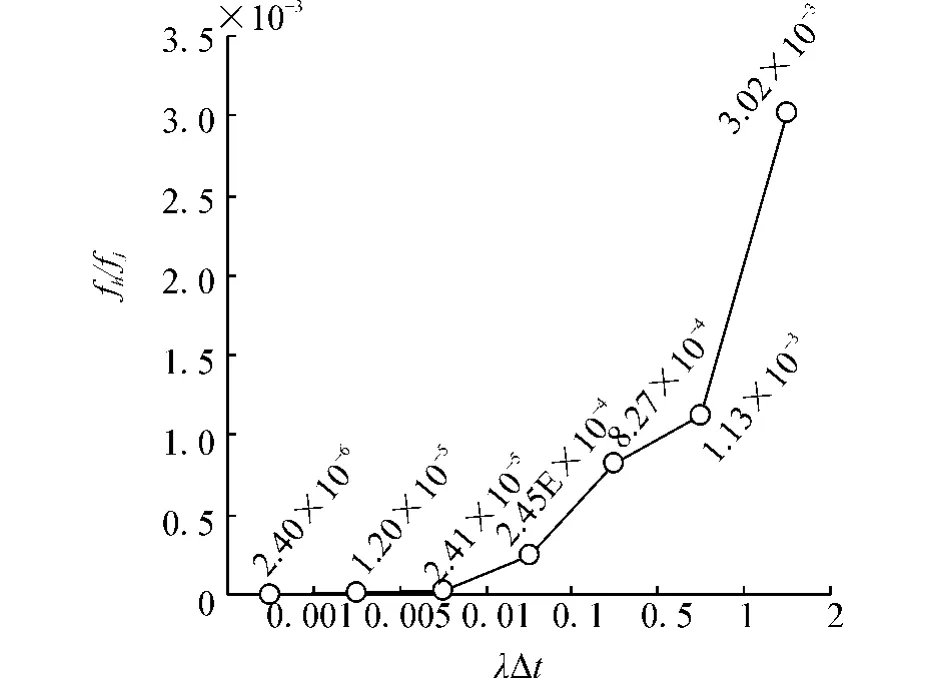
图11 x=10，ε=0.2，α=1.2时fh/fj的比值Fig.11 fh/fj when x=10，ε=0.2，α=1.2

可以看出 fh性能远远优于 fj，在正常情况下(0.001 ＜ λΔt＜0.1)，fh优于 fj达到104量级。在 λΔt=2时，也可以达到103的量级。因此可以得出fh远远优于fj。令α取不同数值，检测其对模型性能影响，如图12所示。随着α的变化，fh先降低后升高，在α=1.4左右时fh最小，性能最好。

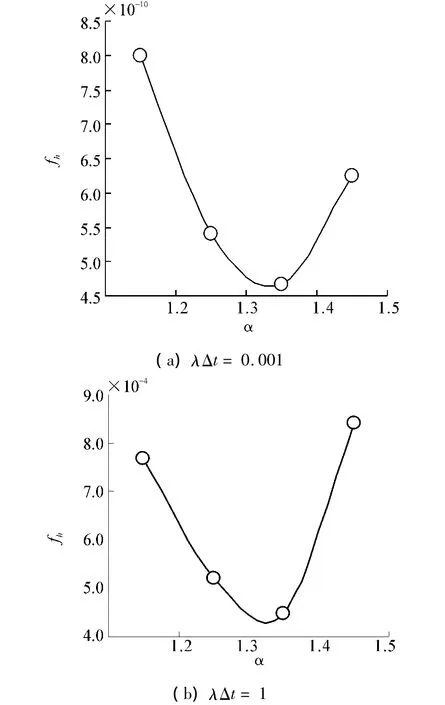
图12 λΔt=0.001和1时α变化对fh影响分析Fig.12 Analysis of αchange impact on fh whenλΔt=0.001 and 1

同样取fh与 fc和 fh与fa的比值，如图13、14所示，fh性能由于二者2～3个数量级，优势明显。

图13 x=10，ε=0.2，α=1.2时fh/fc的比值Fig.13 fh/fc when x=10，ε=0.2，α =1.2

图14 x=10，ε=0.2，α=1.2时 fh/fa的比值Fig.14 fh/fa when x=10，ε=0.2，α =1.2

4 结束语

编码解码、分块存储、动态恢复3种机制的有效融合可以在现有网络存储环境下大幅提升数据的可靠性，本文通过有效融合3种方法，提出了多种数据可靠性评估模型，模拟分析显示本文的模型较先前的多副本(分块)存储、编码存储具有更高的可靠性。通过应用模型可以为具有高可靠性数据存储需求的服务提供网络存储机制和节点选择方法。通过模拟分析和比较正常和异常网络情况下模型的可靠性评估结果，增强了模型的可用性和实用性。

［1］陈兰香，许力.云存储服务中可证明数据持有及恢复技术研究［J］.计算机研究与发展，2012，49:19-25.CHEN Lanxiang，XU Li.Cloud storage service can prove data held and recovery technology［J］.Computer Research and Development，2012，49:19-25.

［2］孟小峰，慈祥.大数据管理:概念、技术与挑战［J］.计算机研究与发展，2013，50(1):146-169.MENG Xia of eng，CIXiang.Big data management:concepts，technology，and challenges［J］.Computer Research and Development，2013，50(1):146-169.

［3］YU Xiangzhan，WU Guanjun.An disaster tolerance model based on dataflow replication［C］//Proceedings of the 2008 IEEE International Conference on Information Automation.Zhangjiajie，China，2008:1590-1594.

［4］PITKANEN M，MOUSSA R.Erasure codes for increasing the availability of grid data storage［C］//International Conference on Internet a n d Web Applications and Services-AICT/ICIW＇06.Guadeloupe，France，2006:1-10.

［5］曲明成，吴翔虎，廖明宏，等.一种数据网格容灾存储模型及其数据失效模型［J］.电子学报，2010(2):315-320.QU Mingcheng，WU Xianghu，LIAO Minghong，et al.A data grid disaster recovery storage model and its data failure model［J］.Chinese Journal of Electronics，2010(2):315-320.

［6］WILKINS R S，DU Xing.Disaster tolerant wolfpack geoclusters［C］//Proceedings of the 2002 IEEE International Conference on Cluster Computing.Chicago，USA，2002:1-6.

［7］WANG Yanlong，LI Zhanhuai.RWAR:a resilient windowconsistent asynchronous replication protocol［C］//Proceedings of the The SecO International Conference Availability，Relaibility and Security.Vienna，Austria，2007:499-505.

［8］YANG C T，WANGSY，WILLIAM CC.Implementation of a dynamic adjustment strategy for parallel file transfer in coallocation data grids［J］.J Supercomput，2010，54:180-205.

［9］GHEMAWAT S，GOBIOFF H，SHUN T L.The Google file system［C］//SOSP＇03.New York，USA，2003:1-15.

［10］The hadoop distributed file system:Architecture and design［EB/OL］.［2013-09-13］.http://hadoop.apache.org/common/docs/r0.18.0/hdfs_design.pdf.

［11］曲明成，吴翔虎，廖明宏，等.一种数据网格存储模型与并行传输调度算法［J］.高技术通讯，2010，20(1):26-32.QU Mingcheng，WU Xianghu，LIAO Minghong，et al.A data grid storage model and scheduling algorithm for parallel transmission［J］.High-tech Communications，2010，20(1):26-32.