改进的单轴旋转SINS初始对准方法

王东，李国林

(海军航空工程学院，山东烟台264001)

捷联惯导系统(strapdown inertial navigation system，SINS)采用单轴旋转调制方案，通过对惯性测量单元的转动来对陀螺常值漂移和加速度计零位误差进行调制，消除其对定位精度的影响，提高系统的长时间导航能力［1-4］。该系统常用的对准方法有基于静基座的古典罗经法和卡尔曼滤波法［5-8］。由于在静基座下，捷联惯导系统对准的极限精度受器件误差的制约，考虑到系统本身具有转动控制机构，为多位置对准提供了条件。因此，本文针对单轴旋转捷联系统，在转台辅助下提高对准精度的对准方法进行了详细的分析。

衡量初始对准效果的2个基本准则是:对准精度高，对准速度快［8］。在静基座下，无论是古典罗经对准法还是卡尔曼滤波对准法，由于某些器件误差的可观测性较差［9-10］，导致2种对准方法对准精度都有所限制。另外，由于转台转位可以提高器件误差的可观测性，一些学者研究了通过控制转台使惯性测量单元在不同位置上进行对准来提高对准精度的方案［11-14］。文献［12-13］分别利用分段线性定常系统(piece-wise constant system，PWCS)和李雅普诺夫变换的方法对捷联惯导多位置对准进行可观测性分析，并对多位置对准进行了仿真研究。文献［14］提出利用单轴转位机构的连续旋转提高系统对准精度的方法，但由于连续旋转实现较为困难，因此实际中难以应用。由于罗经对准和卡尔曼滤波对准方法每次对准都需要消耗较长的时间，如果要进行多次、多位置对准，会大大影响系统启动的快速性［15-16］。

1 静基座初始对准误差分析

在捷联惯导系统中，选取东北天(E，N，U)地理坐标系作为导航坐标系(n系)。建立静基座下捷联惯导系统的速度误差方程如下

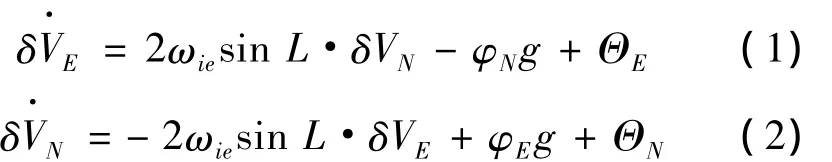
姿态误差方程:

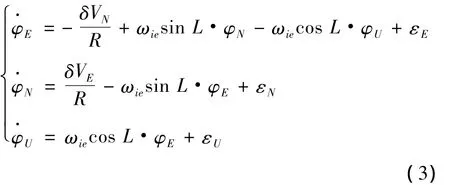
式中:δVE、δVN表示东向、北向速度误差;φE、φN、φU表示东向、北向和方位失准角;ΘE、ΘN表示等效东向、北向加速度计零偏;εE、εN、εU表示等效东向、北向、天向陀螺常值漂移;ωie表示地球自转角速度大小，g为重力加速度，L为当地地理纬度，R为地球半径。

通过将等号左右两边变量调换，可以将式(1)改为

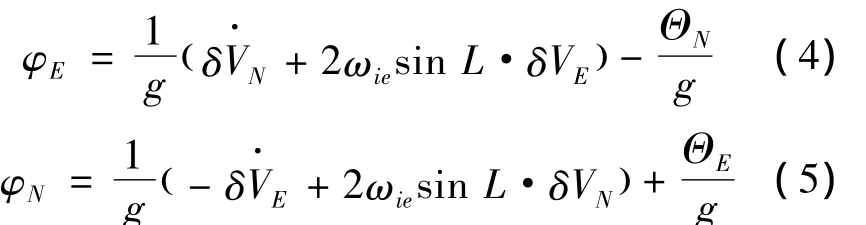
同理，可以将式(3)中的第1个公式改写为

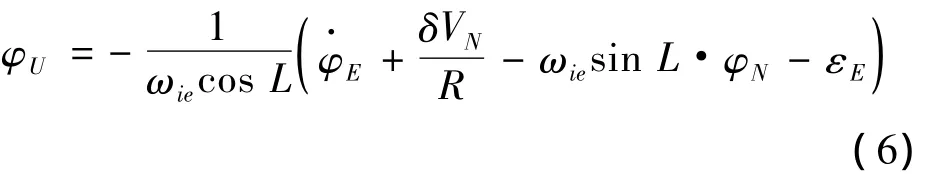
对式(4)两边求导后，联合式(5)共同代入式(6)，可得

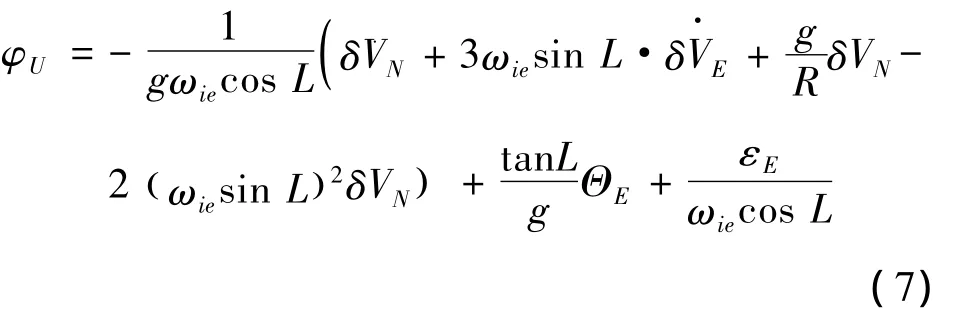
由系统特性所决定，在静基座下 δVE、δVN、、、δV¨N是可观测变量，而 ΘE、ΘN、εE是不可观测变量［9-10］，所以根据式(4)、(7)可知，无论在何种对准方式下，失准角 φE、φN、φU都会存在稳态估计误差ΔφE、ΔφN、ΔφU:

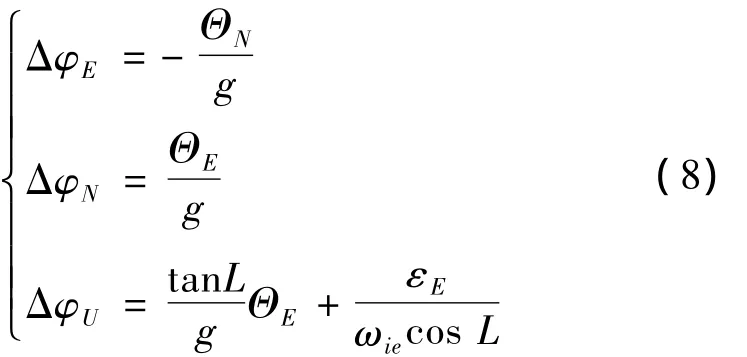
由式(8)知，在静基座下，东向、北向失准角的估计误差分别由等效的北向和东向加速度计零偏引起。对于中等精度的惯导系统(陀螺漂移一般为0.01(°)/h，加速度计零偏一般为10-4g)来说，地球转速为7.292 115 8×10-5rad/s，假设纬度为45°，则陀螺漂移引起的方位失准角大概为0.05°左右，而加速度计零偏引起的方位失准角大概为0.005°左右，所以加速度计零偏的影响 tan L·ΘE/g与陀螺漂移的影响εE/ ωiecos

( L)相比较小，可以将其忽略，则方位失准角主要由东向陀螺漂移引起。

2 基于单轴旋转的初始对准误差修正

利用单轴旋转捷联惯导系统本身存在的转动控制机构，控制转台旋转以消除式(8)中器件误差的不可观测性对对准的影响。初始对准误差修正技术转位方案如图1。

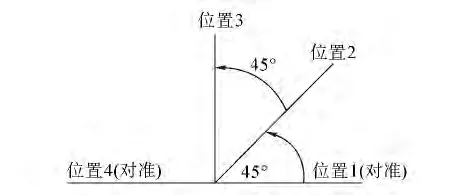
图1 初始对准误差修正技术转位方案Fig.1 Rotation strategy of initial alignment error correction

2.1 东向北向失准角修正

首先记转台任意初始位置为位置1，在位置1进行初始对准，姿态角输出稳定后，记录捷联惯导输出的航向角:

式中:ψ1是真实的航向角，δψ1是位置1处的航向角误差;然后，利用单轴转台将捷联系统绕天向轴旋转45°到达位置2，无需重新对准，直接再次记录捷联系统输出的航向角:

将2次航向角输出作差得到

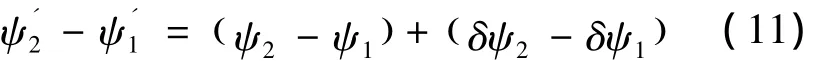
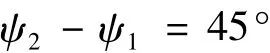
则得到

下面分析δψ1与δψ2的关系:

1)位置1航向角误差表达式。

设在位置1，对准后的失准角误差为ΔφE、ΔφN、ΔφU，且与航向角误差之间存在下列关系［17］:

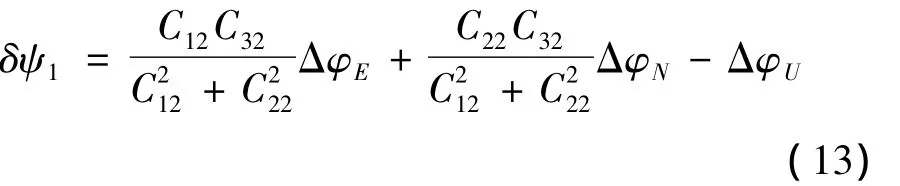
式中:Cij(i，j=1，2，3)为位置1的捷联矩阵中的第i行第j列元素。

2)位置2航向角误差表达式。

由于捷联系统在某一位置上输出的航向角误差包含2个部分，即来自对准误差和来自对准后稳定工作时产生的导航误差。由于只在位置1进行对准，对准后迅速转到位置2，间隔时间较短，所以可以认为2个位置上输出的航向角误差都只包含对准误差，且对准误差也是一样大的。所以，可以得到位置2处的航向角误差

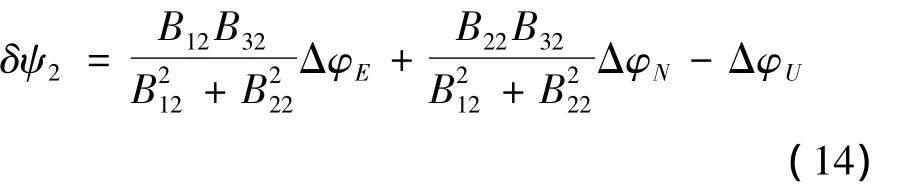
式中:Bij(i，j=1、2、3)为位置2处的捷联矩阵中的第i行第j列元素，且与Cij存在下列关系

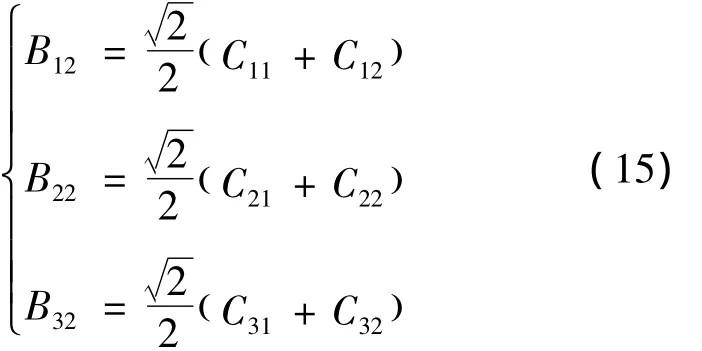
3)位置1和2航向角误差关系。

将式(15)代入式(14)，得到

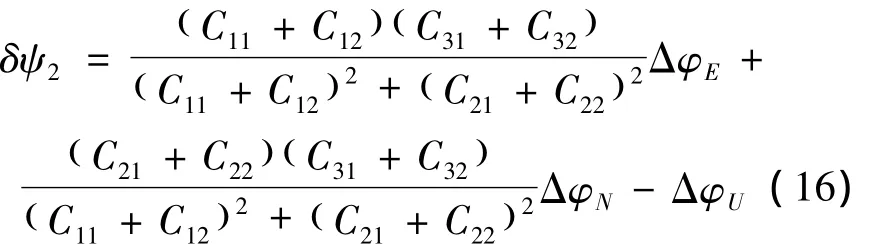
将式(13)、(16)代入式(12)，得到

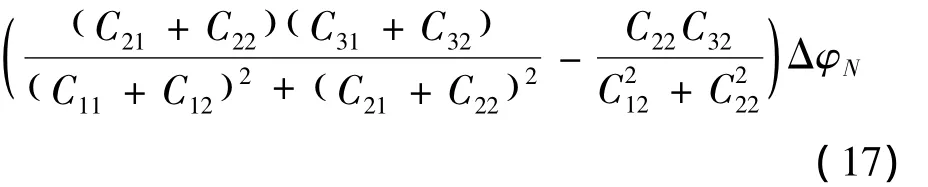
4)位置1和3航向角误差关系。

同理，再次利用单轴转台将捷联系统绕天向轴旋转45°到达位置3，无需重新对准，直接再次记录捷联系统输出的航向角ψ'3，仿照式(10)～(17)，建立位置3与位置1处航向角误差的关系式，如下

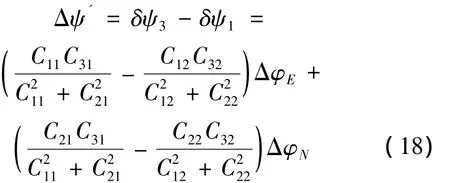
联立方程(17)、(18)可以求解 ΔφE、ΔφN。至此，由于北向，东向加速度计零偏不可观测而引起的东向，北向失准角稳态误差可以通过一次对准，2次转位在短时间内计算出来，补偿以后可以大大提高水平对准的精度。

2.2 方位失准角修正

为了进一步计算方位失准角稳态误差ΔφU，需要再进行一次转位和对准，具体过程如下:

根据式(8)和上一步计算得到的 ΔφE、ΔφN，可以得到位置1的等效东向和北向的加速度计零偏

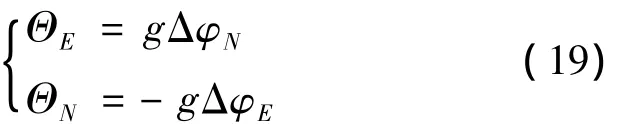
利用位置1的捷联矩阵可以进一步得到载体系上的水平加速度计零偏Θx、Θy:

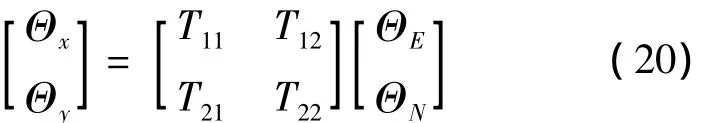
式中:Tij=Cji(i，j=1、2、3)。

在位置3，将捷联系统绕天向轴旋转90°到达位置4，并在位置4重新对准，对准后输出航向角ψ'4:

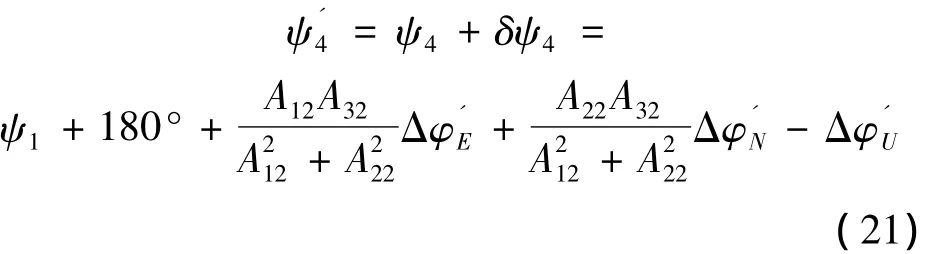
根据 Θx、Θy和 Aij(i，j=1、2、3)可以计算出在位置4的等效东向、北向加速度计零偏、:

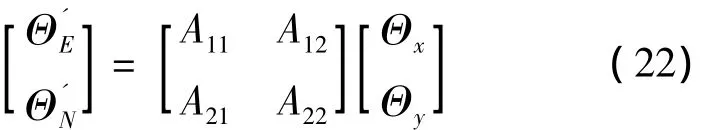
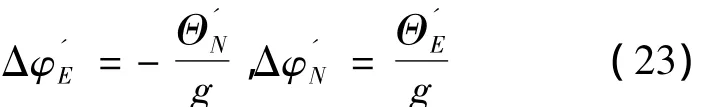
将式(23)代入式(21)，得到

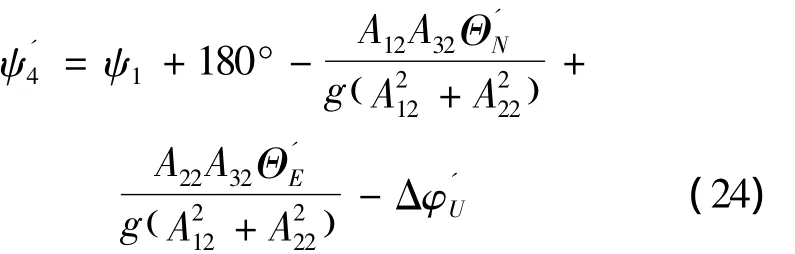
将位置1、4处捷联系统的航向角输出作差，并与理论值180°相减，得到Δψ″:

式(25)中，右边前4项都可以计算得到，相当于已知量，ΔφU和 Δ相当于未知量。

设位置1处的等效东向陀螺漂移为εE，位置4处的等效东向陀螺漂移为，存在下列关系:

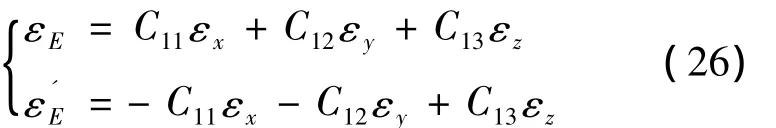
如果认为载体处于水平状态，则可以在上式中忽略C13εz的影响，所以位置1、4两处的等效东向陀螺漂移是大小相等，方向相反的，进而可以认为在1、4两处进行对准，得到的方位失准角误差 ΔφU、Δ是大小相等，方向相反的，即

联立方程(25)、(27)，可以确定ΔφU的大小。

需要注意的是，ΔφE、ΔφN的计算对载体姿态没有要求;而ΔφU的计算是基于载体水平的假设，例如车辆在平稳的路面上，舰船停泊在海港中。如果车辆停在斜坡上或舰船在浪涌的作用下大幅度摇摆，则不能用上述方法确定ΔφU的大小。

实际工程应用中，可以根据具体情况进行不同的初始对准误差修正。如果要求系统快速启动，或载体不处于水平状态，可以只进行1次对准和2次转位，对水平失准角进行修正;如果不要求系统启动时间，且系统处于水平状态，可以通过2次对准，及3次转位将3个失准角全部进行修正，提高系统对准精度。

3 初始对准误差修正仿真试验

为了验证文中提出的单轴旋转捷联系统的初始对准误差修正技术的有效性，进行2组仿真试验。

3.1 对准效果比较

分别与传统的静基座固定位置对准，以及两位置对准进行比较分析，注意3种对准方法在相同的粗对准前提下进行，精对准都采用以速度为观测量的卡尔曼滤波对准。3种对准方法的具体操作如下:

1)静基座固定位置对准。

在粗对准的基础上，在任意固定位置进行卡尔曼滤波精对准，仿真时间30 min。

2)2个位置对准。

在粗对准的基础上，在任意固定位置进行卡尔曼滤波精对准，在第15 min时改变航向角180°，在位置2上再进行卡尔曼对准，仿真时间30 min。

3)基于单轴旋转的初始对准误差修正。

在粗对准的基础上，在任意固定位置进行卡尔曼滤波精对准，停留3min;然后进行两次转位，在每个位置上停留1 min，读取航向角输出，计算水平失准角;进行第3次转位，在第位置4上停留25 min，再次进行卡尔曼滤波精对准。

仿真条件为:陀螺常值漂移为0.01(°)/h;加速度计零偏为1×10-4g;对准的初始误差角分别为:φE=0.1°，φN=0.1°，φU=0.5°;载体初始姿态角:θ=0°，γ =0°，ψ =40°;纬度 L=45.779 6°，经度λ=126.670 5°。仿真结果如图2所示。

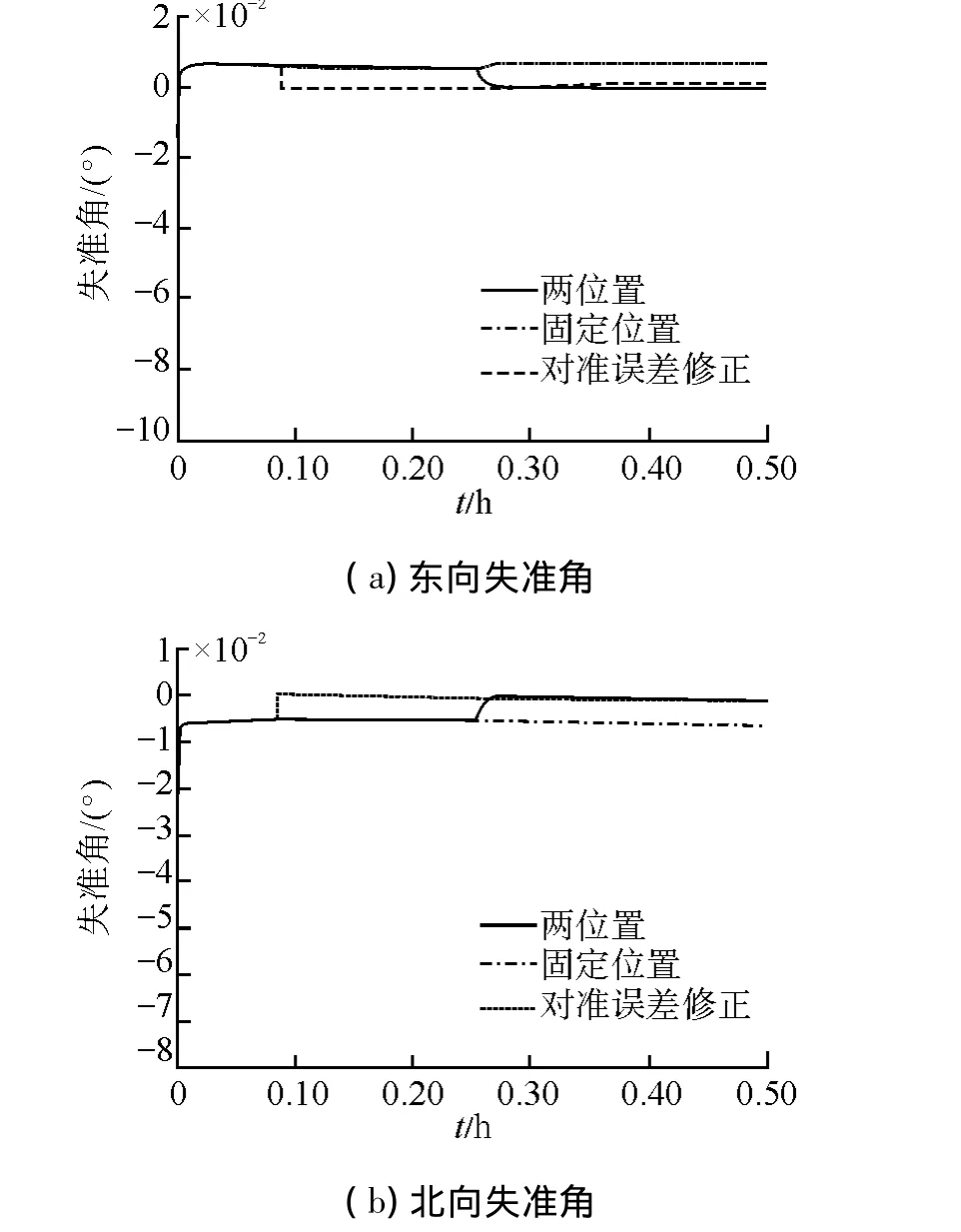
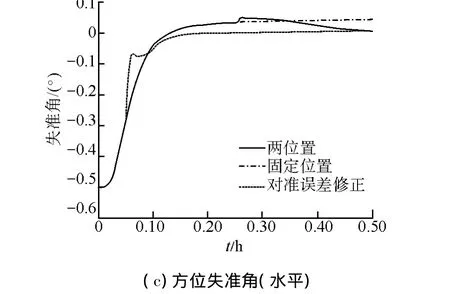
图2 东向失准角、北向失准角、方位失准角估计误差Fig.2 Estimated errors of east m isalignment angle，north m isalignment angle and azimuth m isalignm ent angle(level)

通过图2可以看出，固定位置对准中的失准角在达到稳态时，都存在稳态差值。其中，水平失准角大概存在0.005°左右的稳态误差，而方位失准角大概存在0.05°左右的稳态误差，这与静基座初始对准误差分析的结果(如式(6)所示)是一致的;2个位置对准与固定位置对准相比，对准精度显著提高，在到达位置2以后，稳态误差明显减小，但是2个位置对准的时间较长，特别是方位失准角，在30 min以后才趋于稳定收敛状态;初始对准误差修正方法可以使失准角快速的达到收敛，而且几乎没有稳态误差，2个水平失准角在6 min左右就已经收敛，方位失准角在12 min左右可以达到收敛。由仿真结果可以，与2个位置对准方法相比，利用本文中提出的初始对准误差修正技术可以使得东向水平失准角、北向水平失准角及方位失准角的对准误差得到显著下降。

3.2 载体不水平对ΔφU估计结果的影响

在第2节ΔφU的推导中，需要假设载体处于水平状态，在实际应用中，可能无法满足水平的假设条件。为此，仿真载体不水平对ΔφU估计结果的影响，仿真条件与3.1节相同，但载体初始姿态角设为:θ=5°，γ =7°，ψ =40°。由于水平失准角不受影响，所以只给出方位失准角估计结果，仿真结果如图3所示。

从图3可以看出，由于载体不水平，导致z轴陀螺漂移在水平面上存在投影，使得式(25)不成立，计算出的ΔφU存在常值误差，进而利用含有误差的ΔφU修正方位失准角反而会导致方位对准精度下降。由表1可知，在载体不水平时利用文中提出的初始对准误差修正技术对准得到的方位失准角对准精度较两位对准方法低，所以如果实际应用中载体不水平，应避免对ΔφU进行修正。

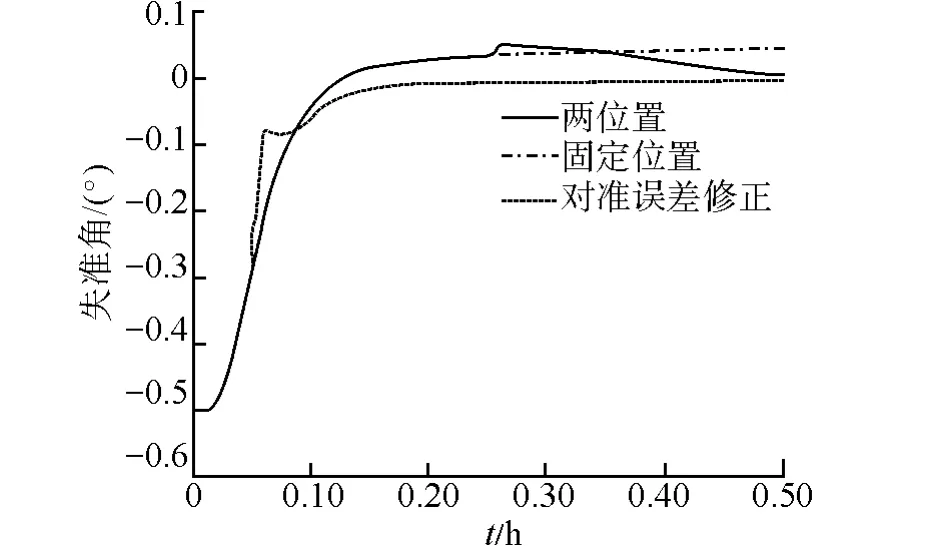
图3 方位失准角估计误差(不水平)Fig.3 Estimated error of azimuth m isalignment angle(not level)

4 结束语

本文针对单轴旋转SINS传统静基座初始对准中，东向、北向加速度计零偏和东向陀螺漂移可观测性较差，从而导致失准角对准结果存在稳态误差的问题，利用系统中自带的转动控制机构，通过两次简单转位，无需重复进行对准，就可以计算出水平失准角稳态误差，从而在缩短对准时间的同时提高了对准精度。如果载体处于水平状态，还可以通过增加一次转位和一次对准的操作，计算出方位失准角稳态误差，提高系统整体对准精度。通过仿真试验可以看出，在载体处于水平状态时，利用文中提出的初始对准误差修正技术可以使得东向水平失准角、北向水平失准角及方位失准角的对准误差得到显著下降。

［1］LEVINSON E，MAJURE R.Accuracy enhancement techniques applied to the marine ring laser inertial navigation［J］.Journal of the Institute of Navigation，1987，34(1):64-86.

［2］孙枫，孙伟，郭真.基于IMU旋转的捷联惯导系统自补偿方法［J］.仪器仪表学报，2009，30(12):2511-2517.SUN Feng， SUN Wei， GUO Zhen.Auto-compensation method of SINSbased on IMU rotation［J］.Chinese Journal of Scientific Instrument，2009，30(12):2511-2517.

［3］LAHHAM J I，BRAZELL JR.Acoustic noise reduction in the MK49 ships inertial navigation system［C］//IEEE Position Location and Navigation Symposium.Monterey，USA，1992:32-39.

［4］LEVINSON E，WILLCOCKS M.The nextmarine inertial navigation is here now［C］//IEEE Position Location and Navigation Symposium.Las Vegas，USA，1994:121-127.

［5］郝燕玲，张义，孙枫.单轴旋转式捷联惯导方位对准研究［J］.仪器仪表学报，2011，32(2):309-315.HAO Yanling，ZHANG Yi，SUN Feng.Analysis of single-axial rotation SINS azimuth alignment［J］.Chinese Journal of Scientific Instrument，2011，32(2):309-315.

［6］汪滔，吴文启，曹聚亮.基于转动的管线陀螺捷联系统初始对准研究［J］.压电与声光，2007，29(5):519-522.WANG Tao，WUWenqi，CAO Juliang.Study on initial alignment of fiber optic gyro SINS based on rotation［J］.Piezoelectectrics＆ Acoustooptics，2007，29(5):519-522.

［7］李瑶，徐晓苏，吴炳祥.捷联惯导系统罗经法自对准［J］.中国惯性技术学报，2008，16(4):386-389.LIYao，XU Xiaosu，WU Bingxiang.Gyrocompass self-alignment of SINS［J］.Journal of Chinese Inertial Technology，2008，16(4):386-389.

［8］万德钧，房建成.惯性导航初始对准［M］.南京:东南大学出版社，1998:7-9.WAN Dejun，FANG Jiancheng.Initial alignment of inertial navigation ［M］.Nanjing:Southeast University Press，1998:7-9.

［9］GOSHEN-MESHIN D，BAR-ITZHACK I Y.Observability analysis of piece- of wise constant system，part I:theory［J］.IEEE Transactions on Aerospace and Eleectronic Systems，1992，28(4):1056-1067.

［10］GOSHEN-MESHIN，BAR-ITZHACK IY.Observability analysis of piece- of wise constant system，part II:application to inertial navigation in-flight alignment［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28(4):1068-1075.

［11］FANG JG，WANG D J.A fast initial alignmentmethod for strapdown inertial navigation system on stationary base［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32(4):1501-1505.

［12］金翔，王大海.光纤陀螺捷联系统最优多位置对准［J］.中国惯性技术学报，2003，11(4):9-13.JIN Xiang，WANG Dahai.Multiposition alignment of fiber optic gyro strapdown inertial navigation system ［J］.Journal of Chinese Inertial Technology，2003，11(4):9-13.

［13］刘志琴，王新龙.捷联惯导系统最优多位置对准的确定与分析［J］.北京航空航天大学学报，2013，39(3):330-334.LIU Zhiqing，WANG Xinglong.Confirmation and analysis on the optimalmultiposition alignment of strapdown inertial navigation system ［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(3):330-334.

［14］孙枫，孙伟.旋转捷联惯导系统精对准技术［J］.系统工程与电子技术，2010，32(3):630-633，659.SUN Feng，SUNWei.Fine alignment by rotation in strapdown inertial navigation systems［J］.System Engineering and Electronics，2010，32(3):630-633，659.

［15］JIANG Y F，LIN Y P.Error estimation of INS ground alignment through observability analysis［J］.IEEE Transaction on Aerospace and Electronic Systems，1992，28(1):92-97.

［16］徐晓苏，孙学慧，扶文树.弹载捷联惯导系统快速两位置对准［J］.中国惯性技术学报，2007，15(2):139-142.XU Xiaosu，SUN Xuehui，FU Wenshu.Fast two-position self-alignment inmissile SINS ［J］.Journal of Chinese Inertial Technology，2007，15(2):139-142.

［17］杨艳娟，卞鸿巍，田蔚风.一种新的INS/GPS组合导航技术［J］.中国惯性技术学报，2004，12(2):23-26，35.YANG Yanjuan，BIAN Hongwei，TIAN Weifeng.A new INS/GPS integrated navigation technique［J］.Journal of Chinese Inertial Technology，2004，12(2):23-26，35.