基于MUSIC算法多脉冲采样的ARM抗诱饵测向误差分析

司伟建，朱曈，张梦莹

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001)

雷达有源诱偏系统作为对抗反辐射导弹(antiradiation-missile，ARM)的有效手段之一，已逐渐被各国应用于各大雷达系统之中，在当今激烈的电子对抗环境下对ARM提出的严峻挑战。为此相关领域的学者提出很多ARM对抗诱饵的方法，其中采用空间谱估计超分辨测向算法是ARM抗诱饵的主要方法之一［1-4］。然而将超分辨测向体制应用于ARM来对抗诱饵时，算法的估计性能会由于真实电磁环境中的种种局限而有所下降［5-8］。多重信号分类法(multiple signal classification，MUSIC)作为超分辨测向算法中的主要代表算法之一，其理论估计性能已被众多学者分析给出［9-11］，但其测角误差是以理想状况下采样数据相互独立为前提推导得到的。

以往干涉仪测向方法每次有效估计可以在一个单脉冲之内完成，因此又称单脉冲测向［12］。与此不同的是，超分辨测向算法往往需要大量采样数据(快拍数)作为保证［13］，才能进行单次的有效估计，因此参与计算的数据往往是由多个脉冲内的采样数据累积而成。对于同一脉冲内的采样数据，由于采样间隔时间很短，使得各辐射源之间有很强的相干性;而对于不同脉冲内的采样数据，相隔的采样时间较长，由于频率、相位漂移等原因，各辐射源之间恢复为非相干状态。因此采样数据中会具有分组相关的特点，即每个脉冲内的数据具有相干性，而不同脉冲内的数据不具有相关性。这使得实际应用中超分辨算法的测向性能相比于理论值有所降低。

本文以MUSIC算法为例，将ARM应用超分辨算法时的测向误差进行推导，得出最优估计时各组观测数应满足的关系，并计算出测向误差期望值的近似结果。通过仿真给出估计有效比——估计误差与克拉美罗界之比随信噪比、信号源数、阵元数及脉冲数的变化曲线，并通过对随机矩阵的条件数分析，得到测向误差的波动程度随脉冲数的变化关系。

1 观测数据分组相关的数学模型

设雷达与诱饵信号共计n个，入射到ARM被动雷达导引头的M阵元天线阵列上，当近似为窄带远场信号时，其观测矢量 X(t)=［x1(t)x2(t)…xM(t)］T可以表示为

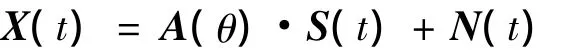
式中:A(θ)= ［a(θ1)a(θ2)…a(θn)］是天线阵列的方向矩阵，a(θi)为导引矢量;S(t)=［s1(t)s2(t)…sn(t)］T是波达方向为 θ1，θ2，…，θn的雷达与诱饵入射信号矢量;N(t)=［n1(t)n2(t)…nM(t)］T表示加性的零均值高斯噪声矢量，方差为σ2N。当噪声与信源之间相互独立时，观测数据的协方差矩阵为

式中:RS=E［SSH］，RN=E［NNH］，当噪声为白噪声时，有RN=σ2NIM×M。在实际中协方差矩阵R是通过L个观测数据得到的估计值近似获得。当单次方位估计所用数据是由多个脉冲内采样累积得到时，由于每个脉冲内强相关性的存在使得式(1)中的RS不再表征E［SSH］，而是与每个脉冲内各信源相差的相位复常数e-jφn有关。

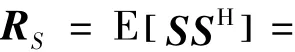
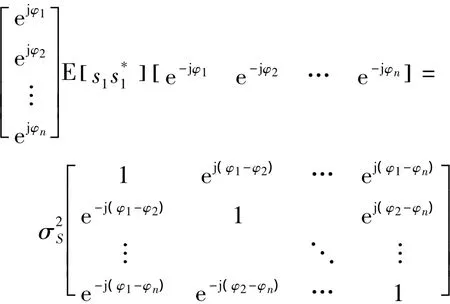
式中:ejφ1=1。

设L个观测数据是从k个脉冲中依次采样得到，令每个脉冲中的观测数据为一组，每组观测数分别为 n1，n2，…，nk，显然有

若构造第i组的相位复常数矢量为

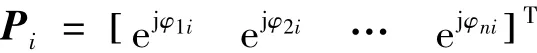
式中:ejφni(i=1，2，…，k，且 ejφ1i=1)表示第 i组的观测数据中第n个信源与第1个信源相差的相位复常数。设第i组的入射信号矢量为Si(t)，则第i组的信号协方差矩阵RSi可以写为

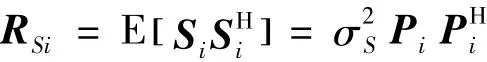
由于不同波门下采样间隔较长，受到频率、相位漂移等原因导致其不同组间的相位复常数ejφ发生变化，可以认为这种变化是随机的，即满足 φ在[ 0，2π)上的均匀分布，则信号协方差矩阵的估计值可以写为

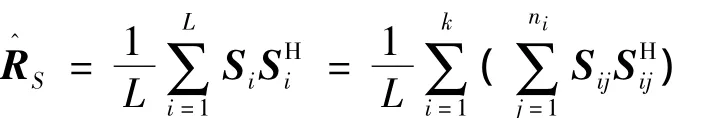
则式(1)中RS实际为

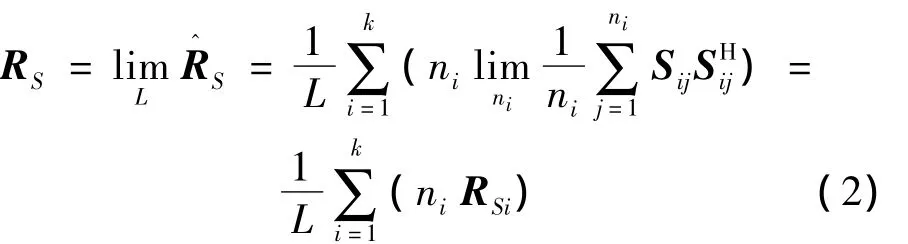
2 多脉冲采样时MUSIC估计误差分析

根据MUSIC估计器的原理:

可知必定有

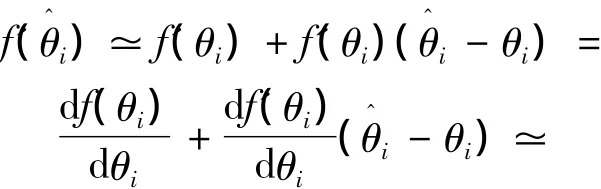
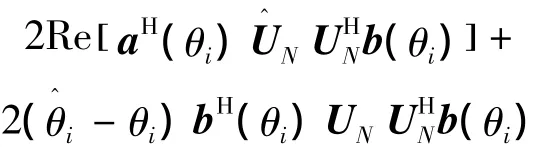
式中:b(θi)，因此估计误差- θi可以

写为

可以得到估计误差的方差［9］:

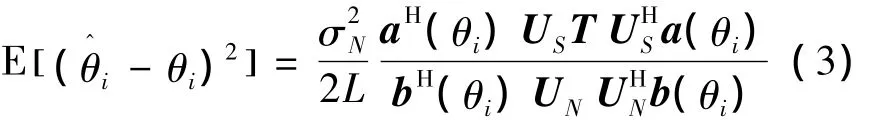
令 λ1，λ2，…，λn是信源对应的 n 个特征值，则

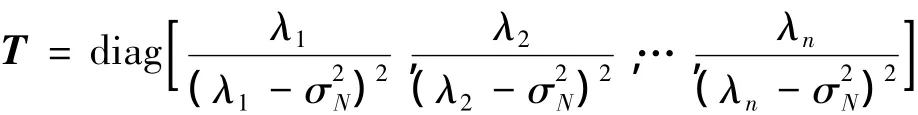
为了避免计算特征分解的麻烦，再根据恒等式:

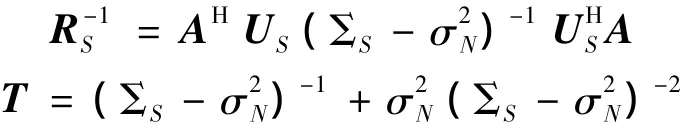
代入式(3)可以化为

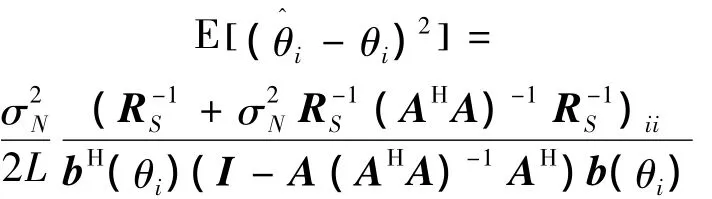
式中:(·)ii表示矩阵的第i个对角元素。根据前文分析，当观测数据具有分组相关特性时，R-1S中也含有随机成分，即上式应写为

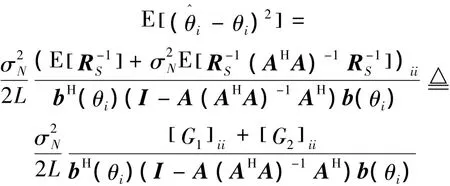
注意到当每组观测数 n1，n2，…，nk变动时，根据不等式，故对于方差D[ R]始

S终有

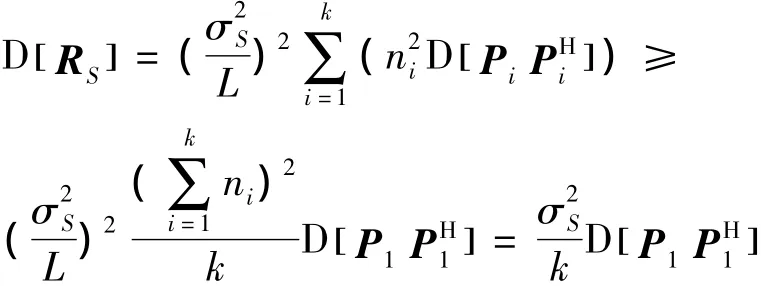
等号在n=n=… =n=

12k时成立，即说明当总快拍数L一定时，每组的观测数相等时估计的有效性最高。在满足此条件时式(2)可以化简为

则

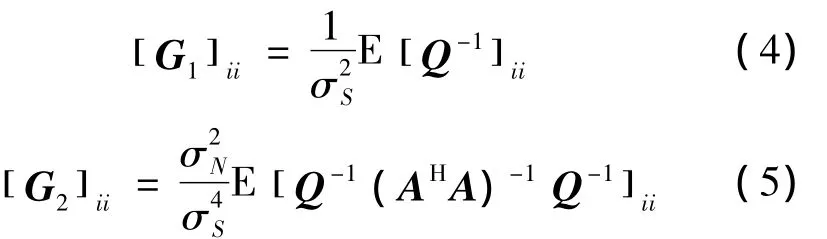
即只需计算出 [ G1]ii与 [ G2]ii的期望值，就可得到MUSIC算法在多脉冲采样时观测数据具有分组相关性的测向估计误差。

2.1 [ G1] ii的求取

为分别求出 [ G]与 [ G]，首先将E [ Q-1]

1ii2iiii

写为

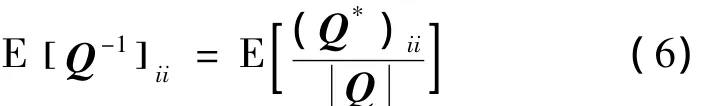
式中:Q*表示Q的伴随矩阵。根据行列式展开可知，对于Q= [ qij]n×n有

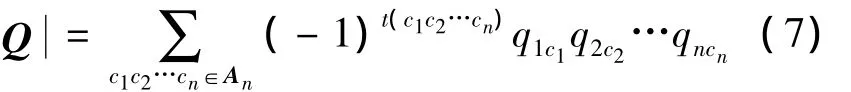
式中:An表示1～n的排列全集，t(·)是排列的逆序数。通过观察矩阵Q可以发现，对于其元素qij有

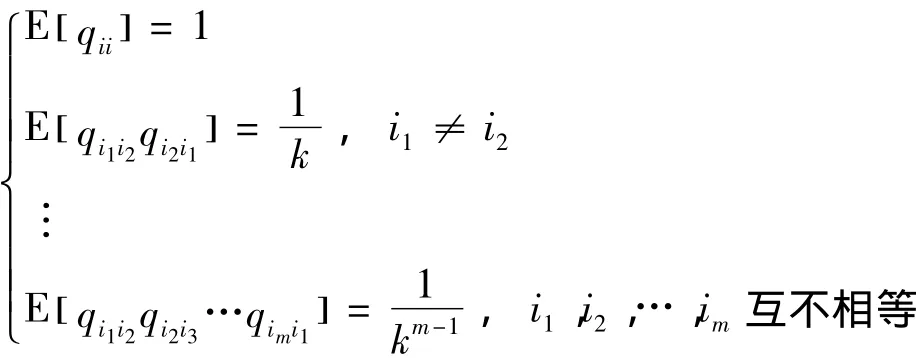
故可将所有项q1c1q2c2…qncn按含有qi1i2qi2i1(i1≠i2)的个数分类。若令μ(ni)表示n维方阵中选取i对qi1i2qi2i1(i1≠i2)的选法总数(此时任2个元素不可同行或同列)，υm表示 m维方阵中 qi1i2qi2i3…qimi1，(i1，i2，…，im互不相等)的选法总数，图例如图1。

图1 μ(n i)与 υm的含义图例Fig.1 Definition of μ(ni)andυm

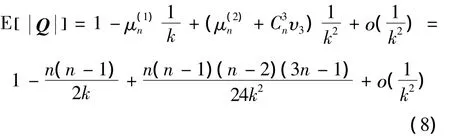
观察到矩阵Q的对角元素均为1，由式(8)可知当k一定时，E [Q]与E[(Q*)ii]只与信源数n有关，且根据随机相位的独立性可知E[(Q*)11]=E[(Q*)22]=…=E[(Q*)nn]。用下角标Qn记做矩阵Q的维数，则式(6)可以化简为

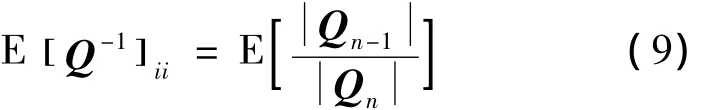
注意到当k增大时对任意n≥1，矩阵Q满足

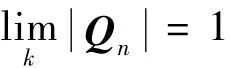
记

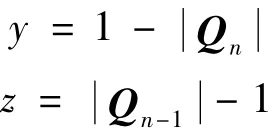
则将式(9)在y=0处Taylor展开，有

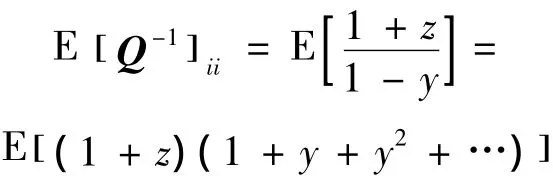
综上，可以得到 [ G1]ii的近似值为

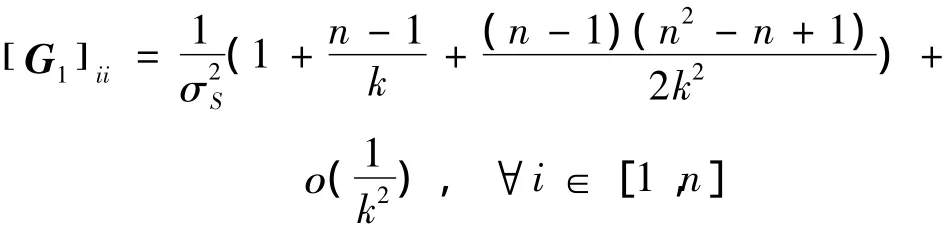
2.2 [ G2] ii的求取

同理可以计算 [ G2]ii的值，由于随机矩阵Q是对角占优矩阵，所以式(5)可以转化为

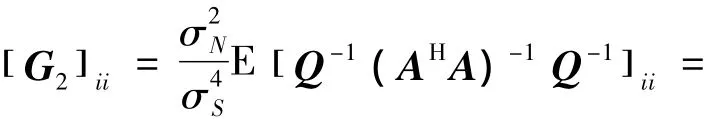
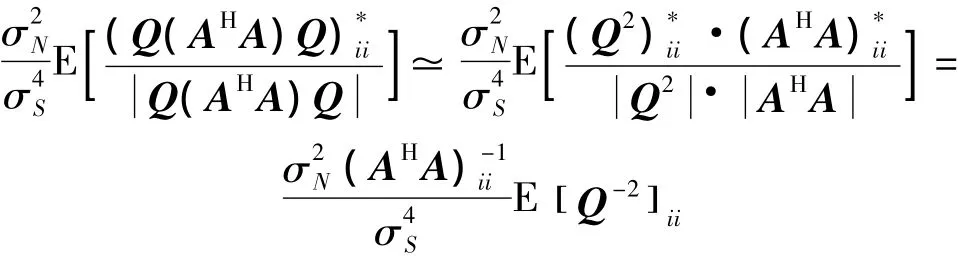
根据式(7)行列式的定义有

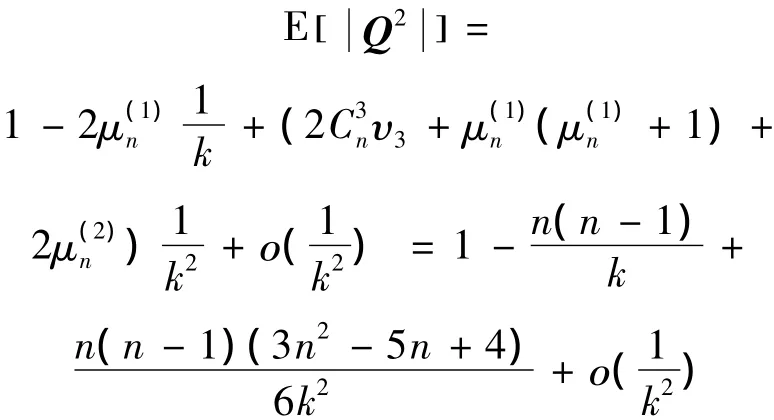
需要注意的是E[ (Q2]≠，若将矩阵Q写为分块矩阵:

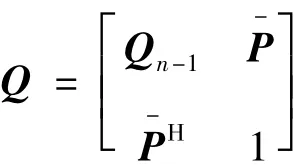
则可以看出

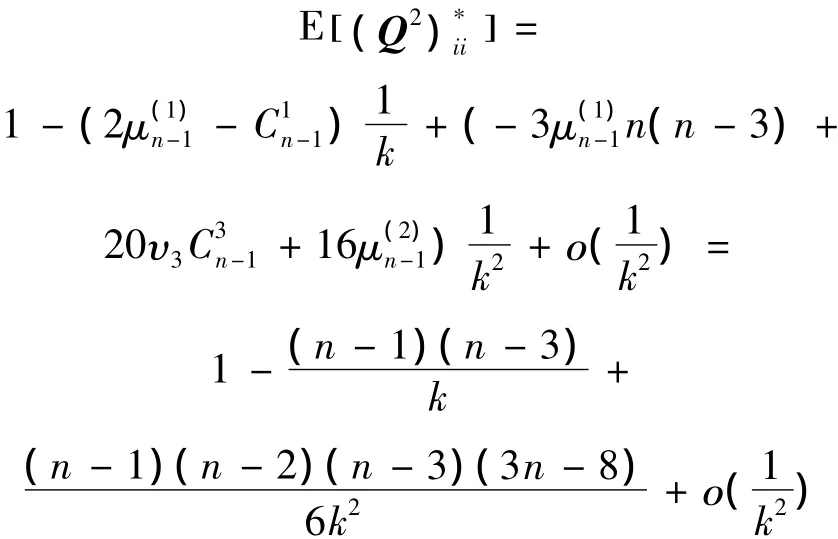
则根据式(6)的原理可以得出 [ G2]ii的值:

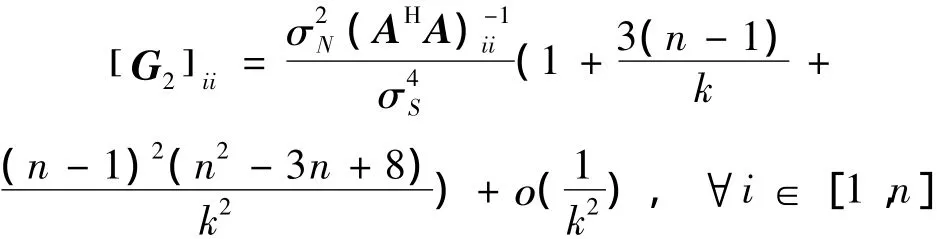
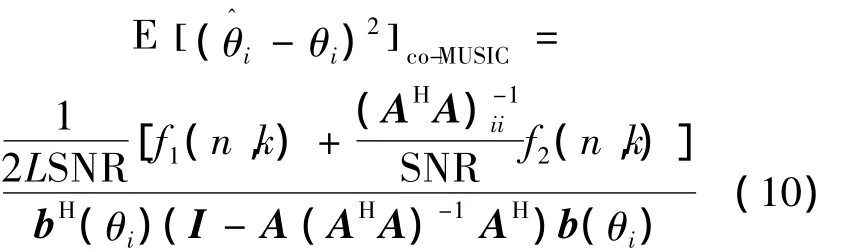
式中:

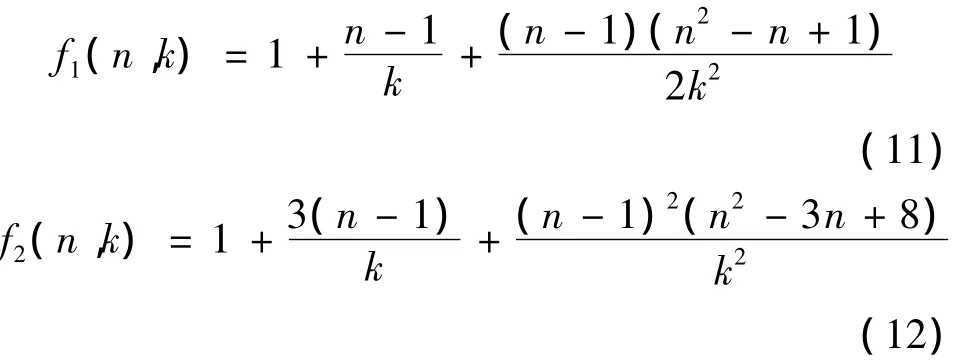
2.3 关于式(10)的几点讨论

1f2(n，k)⋍1，此时测向估计方差还原为经典MUSIC算法的方差

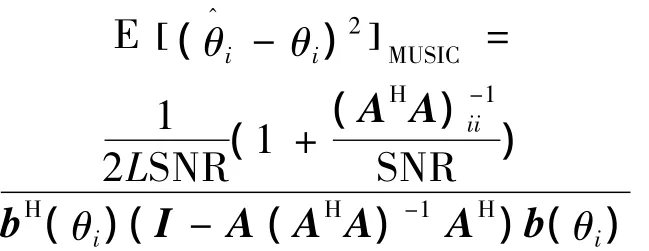
2)当k＜n时，矩阵Q为奇异阵，此时Q的逆阵不存在，理论估计误差也不存在。这是由于此时信源仍含有相干成分，未经过预处理的MUSIC算法将完全失效。因此可以得出相关采样组数k的基本要求为k≥n。

3)当k≥n且k不是很大时，随机矩阵Q的波动性——即矩阵Q中的任一随机相位的微小变动所引起的Q逆阵变化的剧烈程度，随着k、n的变化而变化，其病态程度由其条件数cond(Q)决定

cond(Q)=‖Q‖·‖Q-1‖

式中:‖·‖为矩阵的任一范数。由于Q为Hermite矩阵，可以将其谱范数带入上式，有λ(·)为特征值。则当 k、n不同时，条件数 cond(Q)2的变化如表1。

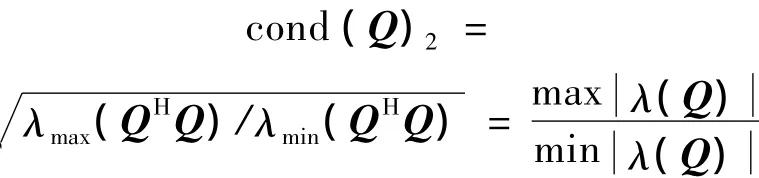
条件数的具体大小与矩阵范数的取法有关，但相对大小一致，因此从表1中可以看出矩阵Q的病态程度随着k值的增大而迅速降低，显然当k趋于无穷时cond(Q)=1，而信源数n的增加会导致矩阵Q的病态程度整体略有增加。该条件数直接反应了随机相位φij变化的波动对估计方差的影响程度，当条件数较大时，意味着测向估计结果对随机相位φij的取值很敏感，相当于有更大概率产生较大误差估计(错误估计)。因此从表1中条件数的变化趋势可以看出，k值的下限取值以k≥n+4为宜。

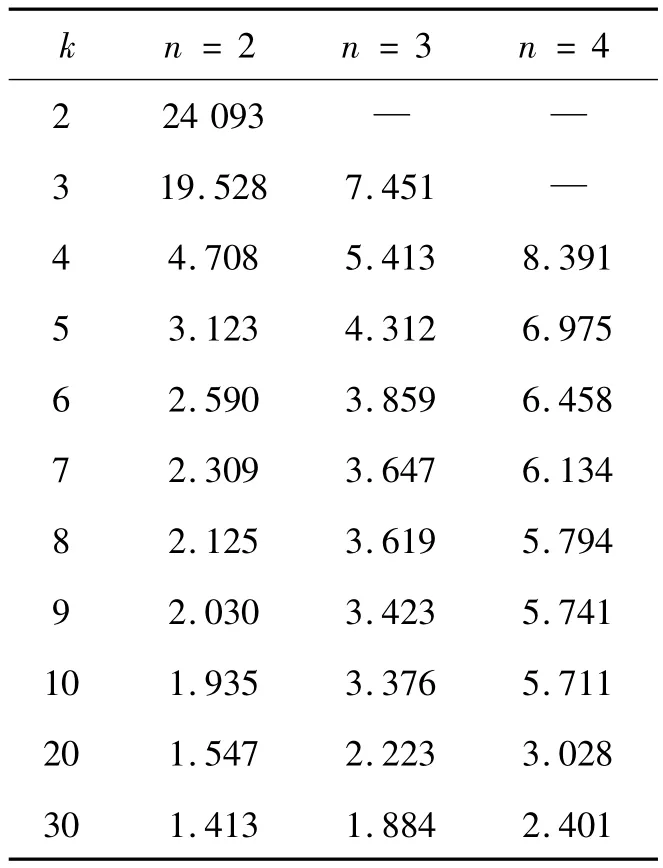
表1 条件数cond(Q)2随k、n变化的趋势Table 1 cond(Q)2 with k，n changes

4)若ARM的天线阵列为二维空间阵列，可以测定的角度为方位角α与仰角β，角度估计θ为α，β 构成的矢量 θ(α，β)，若令

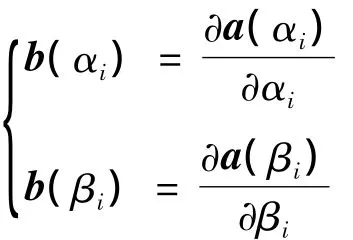
则同理可得方位角α与仰角β的估计方差为

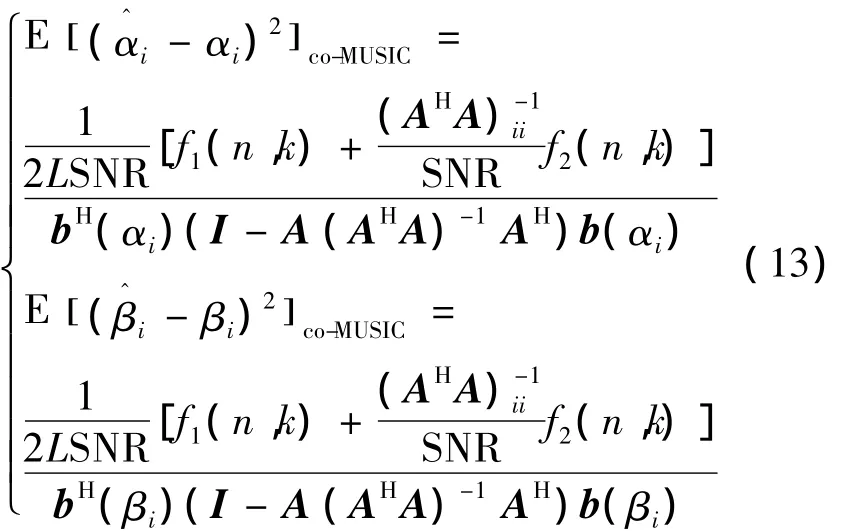
式中:f1(n，k)和 f2(n，k)与式(11)、(12)相同。

3 仿真实验与结果分析

为了对比单脉冲内信号的相关性对测向算法估计误差产生的影响，以经典MUSIC的克拉美-罗界(Cramer-Rao bound，CRB)作为参考，MUSIC算法下等功率信号的CRB以下式给出［10］可定义角度估计有效比

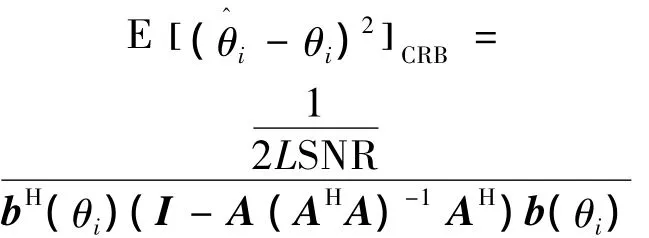
可见估计有效比越高，则表明该估计越接近所能达到的CRB上限。同时，由式(13)可见在二维角度估计时，其估计误差形式与式(10)的一维估计误差形式相近，且估计有效比相同。故本文仿真实验以一维估计为例，并不影响一般性。

设接收天线阵列为5阵元的一维线阵，阵元间距为半波长。若两等功率的远场信号入射角为 θ1、θ2，角度间隔为 Δθ= θ1- θ2，L=100。图2(a)、(b)分别为信噪比为10 dB与0情况下，MUSIC算法的估计有效比理论值与实际中观测数据具有分组相关性时的估计有效比随角度间隔的变化曲线，其中采样脉冲数分别设置为6、10、14。从图2中可以看出分组相关采样下的估计有效比随着脉冲数k与信噪比的增加而增加，且能达到的最高有效比与脉冲数k直接相关，k值越高，越接近理论值。

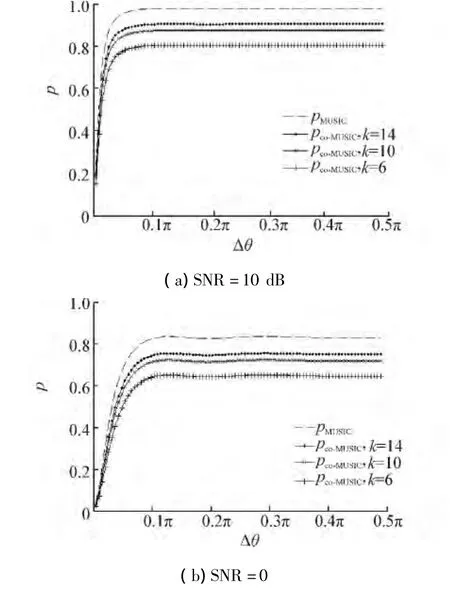
图2 估计有效比与角度间隔的变化曲线Fig.2 Efficiency ratio curves versus angle interval

图3(a)、(b)是信噪比分别为10 dB与0情况下，估计有效比随脉冲数k的变化曲线。接收天线阵列依旧为5阵元的一维线阵，阵元间距为半波长。远场入射信号分别为2、3、4个，角度间隔固定为Δθ=0.05π，L=100。从图3中可以看出，分组相关采样时的估计有效比随着k值的增加而逐渐接近理论值。

图3 估计有效比与脉冲数k的变化曲线Fig.3 Efficiency ratio curves versus the number of pulses k

图4(a)、(b)是信噪比分别为10 dB与0情况下，估计有效比随阵元数M的变化曲线。天线阵列的阵元数依次设置为5、6、7…，阵元间距为半波长。远场入射信号为3个，入射角度设置为 -9°、0°、9°。L=100 ，采样脉冲数分别设置为6、10、14。从图4可以看出分组相关采样时的估计有效比随着阵元数M的增加而增加，最终趋于稳定，能达到的最大有效比与脉冲数k有关。

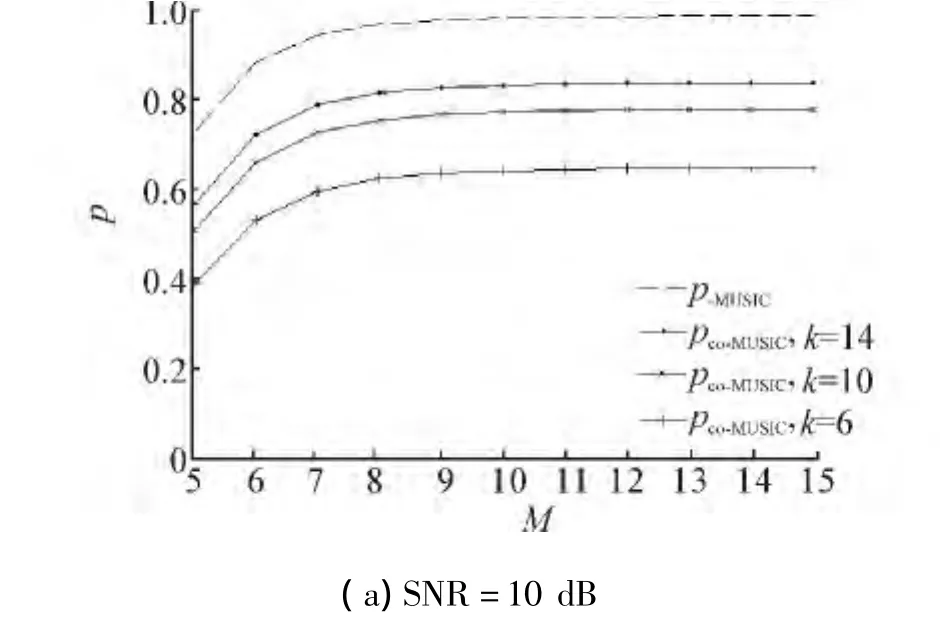
图4 估计有效比与阵元数M的变化曲线Fig.4 Efficiency ratio curves versus the number of antennas M

4 结束语

本文分析了单脉冲内采样数据具有强相干性时，经典MUSIC算法的估计性能会有所下降的原因，式(10)给出了此时估计方差的近似期望值。揭示了ARM采用超分辨算法时的实测估计误差与理论值有较大差异的主要原因之一。仿真结果表明，当采样脉冲数k一定时，测向估计误差的有效比会随着阵元数的增多及入射辐射源角度间隔的增大而提高，但最终将稳定于低于理论值的某一水平。其稳定值与脉冲数k与信源数目n有关，k越高、n越小，则估计有效比越接近理论值。也表明了在实际工程中合理地增加采样脉冲数k可以有效地减小估计误差。

［1］司锡才，崔冬槐，司伟建.反辐射导弹对抗低截获概率雷达和诱饵技术［J］.系统工程与电子技术，2005，27(9):1549-1552.SIXicai，CUI Donghuai，SI Weijian.Technology of ARM contradict LIP radar and bait［J］.Systems Engineering and Electronics，2005，27(9):1549-1552.

［2］司锡才，赵利军.反辐射导弹抗诱饵诱偏技术研究［J］.弹箭与制导学报，2006，26(2):550-553.SIXicai，ZHAO Lijun.Tecnolegy staday of anti-radiation missile contradict bait［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2006，26(2):550-553.

［3］曲志昱，司锡才，朱晓.一种反辐射导弹抗非相干诱饵的新方法［J］.西安电子科技大学学报，2009，36(6):1132-1138.QU Zhiyu，SI Xicai，ZHU Xiao.New method for the anti radar missile to antagonize the non-coherent radar decoy［J］.Journal of Xidian University，2009，36(6):1132-1138.

［4］杨勇，谭渊，张晓发，等.基于MUSIC算法的反辐射导弹抗诱饵诱偏［J］.弹箭与制导学报，2010，30(4):241-243.YANG Yong，TAN Yuan，ZHANG Xia of a，et al.ARM antagonizing bait decoy based on MUSIC algorithm［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2010，30(4):241-243.

［5］刘剑，黄知涛，王延伟，等.通道失配对MUSIC算法测向性能影响研究［J］.空军工程大学学报，2007，8(3):74-77.LIU Jian，HUANG Zhitao，WANG Yanwei，et al.Performance analysis of MUSIC algorithm in the presence of channel mismatch［J］.Journal of Air Force Engineering University，2007，8(3):74-77.

［6］步新玉，洪伟.幅相误差对两类高分辨测向算法性能的影响［J］.舰船电子对抗，2011，34(2):89-91.BU Xinyu，HONG Wei.Influence of amplitude and phase errors on two kinds of high-resolution direction-finding algorithms performance［J］.Shipboard Electronic Countermeasure，2011，34(2):89-91.

［7］陈鑫，王浩丞，唐勇，等.多径环境中被动雷达导引头测向性能分析［J］.电子信息对抗技术，2011(4):1-4.CHEN Xin，WANG Haocheng，TANG Yong，et al.Angle characteristic analysis of PRS inmultipath environment［J］.Electronic Information Warfare Technology，2011(4):1-4.

［8］王鼎，吴瑛.小幅相误差下MUSIC的测向成功概率和分辨概率［J］.电波科学学报，2010，25(4):749-756.WANG Ding，WU Ying.Direction-finding success probability and resolution probability of MUSIC algorithm in the presence of small gain-phase errors［J］.Chinese Journal of Radio Science，2010，25(4):749-756.

［9］STOICA P，NEHORAI A.MUSIC，maximum likelihood，and Cramer-Rao bound［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1989，37(5):720-741.

［10］刘剑，宋爱民，任清华.干涉仪与MUSIC算法的测向原理及精度对比［J］.航空兵器，2012(3):29-32.LIU Jian，SONG Aimin，REN Qinghua.Direction finding principles and accuracy contrast of interferometer and MUISC［J］.Aero Weaponry，2012(3):29-32.

［11］SHRESTHA P L，HEMPEL M.Performance analysis for direction of arrival estimating algorithms［C］//IEEE Vehicular Technology Conference.Yokohama，Japan，2012.

［12］司锡才，赵建民.宽频带反辐射导弹导引头技术基础［M］.哈尔滨:哈尔滨工程大学出版社，1996:27-102.

［13］罗利春.空间谱测向超性能机理与系统评介［J］.中国空间科学技术，1995(1):1-8.LUO Lichun.The mechanism analysis to super-performance of DF using spatial spectrum estimate and real systems introduction［J］.Chinese Space Science and Technology，1995(1):1-8.