微带天线对高功率电磁脉冲响应的时域分析

李磊，张昕

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001)

随着电磁脉冲武器性能的逐步提高，对装有灵敏电子器件的现代电子设备造成毁伤的可能性也越来越大，因而电子设备对电磁脉冲的响应成为国内外研究的热点［1-3］。前门耦合和后门耦合是电磁脉冲能量进入电子设备的2种途径［4-5］。目前国内外对于后门耦合的研究较多，而研究前门耦合的相对较少。虽然天线是主要的前门耦合途径，但对其的研究主要集中于较为简单的线天线。微带天线由于具有重量轻、体积小、剖面薄、易于共形、电性能多样化等优点，被广泛应用于军事和民用通信设备中［6-8］。电磁脉冲的研究属于瞬态电磁学范畴，因而时域有限差分法在处理该问题时具有很大的优势。但时域有限差分法在处理微带天线结构时，由于天线辐射片边缘的电磁场具有奇异性，因而在建模时需要特别处理，否则会导致局部的截断误差［9］。Taflove提出了亚网格技术来细化局部网格划分［10］，但这样减小时间间隔，降低计算效率。Railton等提出了修改材料电参数的方法［11］，提高了计算效率，但对导体嵌入面积大于网格1/2时的情况没有处理方法。

1 基本原理

1.1 渐变非均匀网格原理

由于FDTD采用了电场和磁场在空间中离散排布的Yee元胞，把麦克斯韦旋度方程转化为显式差分方程，使得电场和磁场可以在时间上迭代求解，而不需要进行矩阵的求逆［12］，因而在利用FDTD分析电磁问题时，一个主要影响计算精度的因素就是空间离散间隔，即空间网格尺寸。尽管采用更小的网格大致可以保证需要的计算精度，但同时也使得元胞数量成倍地增长，极大地增加了计算量，延长了计算时间［13］。目前主要有2种情况必须要采用很小的空间网格才能保证计算精度，一种情况是在进行建模时，有不能忽略的细小结构需要精确建模才能保证计算结果的可靠性;另一种情况是计算空间中，某一个区域存在剧烈变化的场，需要很小的空间网格才能准确描述。微带天线同时符合以上2种情况，首先微带天线的基底厚度与其长宽相比较小，其次微带天线的不连续结构周围存在剧烈变化的电磁场。因此在计算微带天线时，基底厚度通常至少需要3个空间网格，网格尺寸一般小于1 mm，如果采用均匀网格建模微带天线，就需要很大的计算空间，进而导致较大的内存消耗和较长的计算时间，计算效率极低。

渐变非均匀网格(variable mesh scheme，VMS)FDTD由choi等［14］提出，其在电磁场变化剧烈处采用小尺寸网格，在电磁场变化平缓处采用大尺寸网格，这种灵活的网格划分方法较好地解决了计算效率与计算精度的矛盾。此外，除空间离散间隔Δx、Δy和Δz的大小在计算空间是变化的之外，VMSFDTD的电磁场更新方程与常规的均匀网格FDTD的相同。

例如，图1所示的Ex和Hx在自由空间的更新方程为:

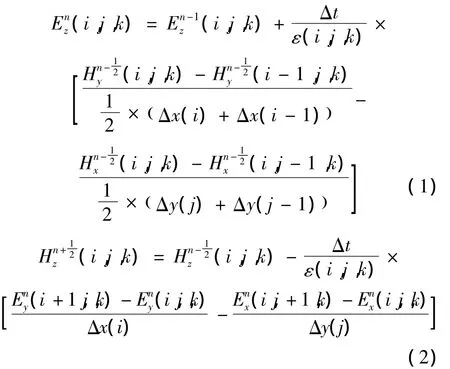
式中:Δx(i)、Δy(j)和Δz(k)为电场或磁场所处元胞的空间离散间隔。其他方向的电场和磁场的更新方程与式(1)、(2)类似。由图1可见，电场Ez不处于磁场网格的中心，且2个相邻的电场网格大小也不相等，因而在计算Ez时，磁场网格的大小被视为两个相邻元胞尺寸和的一半。为保证算法的稳定性，Δt需要满足:

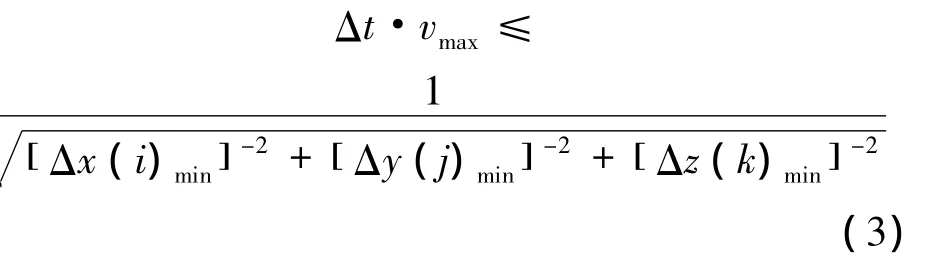
式中:Δx(i)min、Δy(j)min和 Δz(k)min分别为 x、y和z方向的最小离散间。

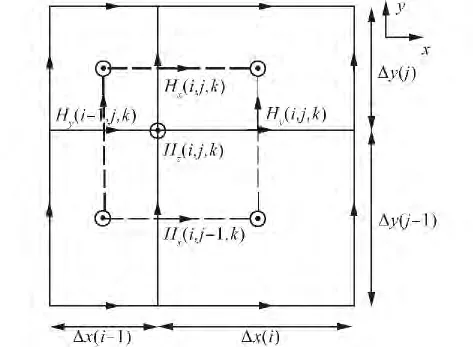
图1 渐变非均匀网格Fig.1 VMS

1.2 导体边缘奇异场处理技术

FDTD在分析不连续结构周围存在剧烈变化的电磁场一般采取更为精细的网格划分方式，但随之会导致计算效率的降低。针对上述问题，为了在大网格划分的基础上保证计算的精度，本文将文献［15］得到的导体边缘场分布函数引入到FDTD中，得到了导体边缘场的FDTD处理方法。

如图2所示的导体边缘场可表示为

国家环保模范城市考核指标包括社会经济、环境质量、环境建设、环境管理四部分。考虑到该地区正在创建模范生态城市，矿区规划环评在指标选取上主要选择了生态环境质量及环境建设的部分指标。

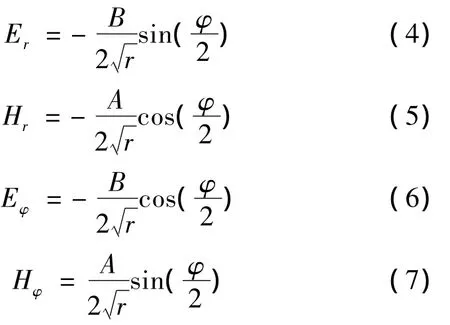
式中:r为导体边缘到场点的距离，φ为二者之间的夹角，A和B为未知系数。由式(4)～(7)可见，由于1/项的存在使得横向场具有奇异性。

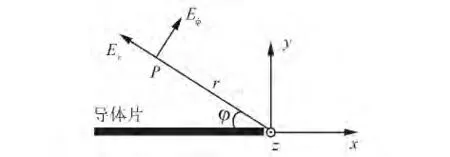
图2 导体边缘横向电磁场Fig.2 Transverse electric and magnetic field components around am et al edge

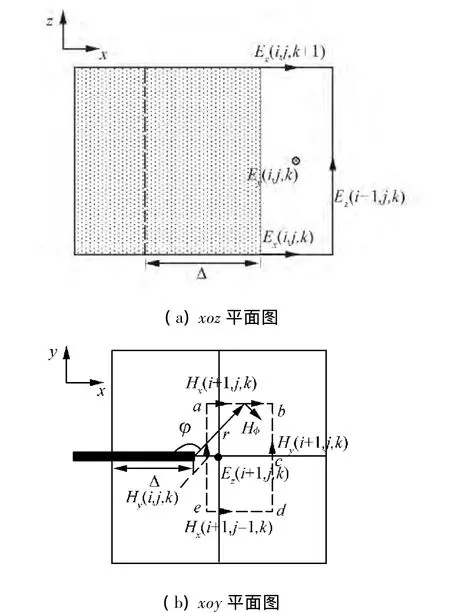
图3 导体嵌入网格平面图Fig.3 Conductors protrude intomesh

现以图3为例说明导体边缘场的奇异性处理方法。由图3(a)可见，导体嵌入网格长度为 Δ，且Δ＞Δx/2，如果按照传统 Yee网格划分方式，则Ex(i，j，k)、Ex(i，j，k+1)和 Hy(i，j，k)均为零，相当于增大了导体嵌入网格的长度，这将导致计算误差，因而本文将 Ex(i，j，k)、Ex(i，j，k+1)和 Hy(i，j，k)3个节点的位置沿x轴移动Δ/2，此时r=(Δx- Δ)/2 ，φ =180o，因而 Hy(i，j，k)=-Hφ，Ex(i，j，k)=Er，由式(4)和(7)可得

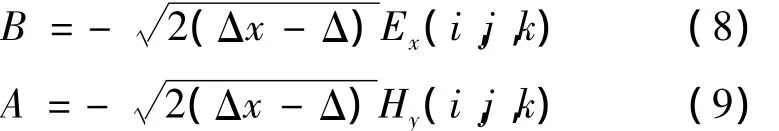
将式(8)、(9)分别代入式(4)、(7)可得导体边缘横向场的分布为

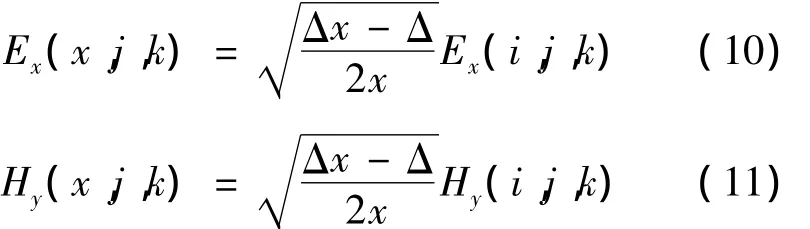
由法拉第定律可得

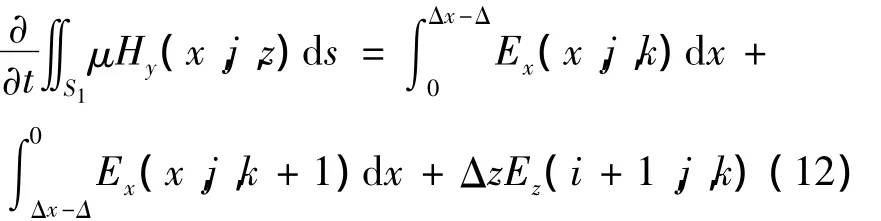
式中:S1为单元网格中未嵌入导体的区域。由式(12)可得

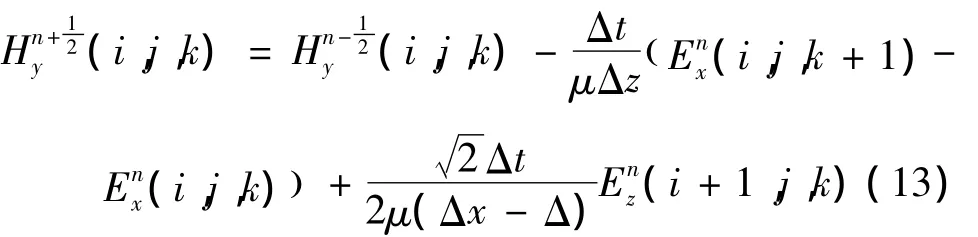
由安培定律计算图3(b)中的 Ez(i，j，k)时，将磁场的线积分分为 ab、bc、cd、de、ef和 fa 共6 段进行计算，则

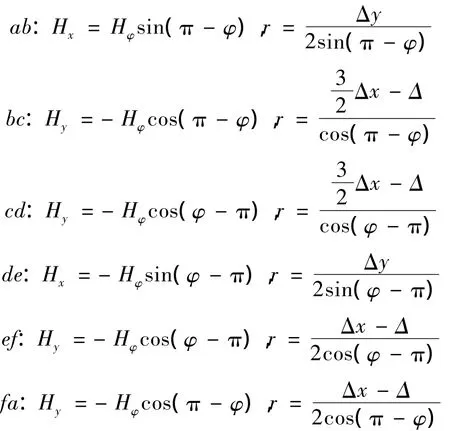
假设Ez在计算网格内均匀分布，则结合式(7)可得

其中，A1、A2和A3可由式(9)类似方法求得

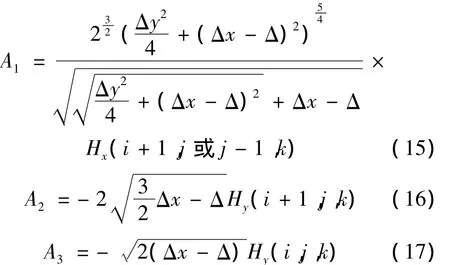
其他场量均可按类似方法处理。

2 天线建模与算法验证

计算模型采用图4(a)所示的微带天线，基板材料采用高频介质板，相对介电常数εr1=2.2，通过同轴线进行馈电，同轴线填充介质为聚四氟乙烯，其相对介电常数εr2=2.1。空间离散间隔是影响FDTD计算精度的主要因素之一，本文采用渐变非均匀网格技术，在天线周围结构不连续处采用较小的离散间隔以模拟剧烈变化的电磁场;另一方面，为了提高计算效率，降低内存消耗，可以在电磁场平缓变化处采用较大的离散间隔。结合微带天线结构，建模时在xoy平面采用 4种离散间隔，即 Δl、1.59Δl、2.52Δl和4Δl，其中最小离散间隔 Δl=0.4 mm(l为x或y)。时间离散间隔Δt=4.514 2×10-13s。微带天线的网格划分如图4(b)所示。

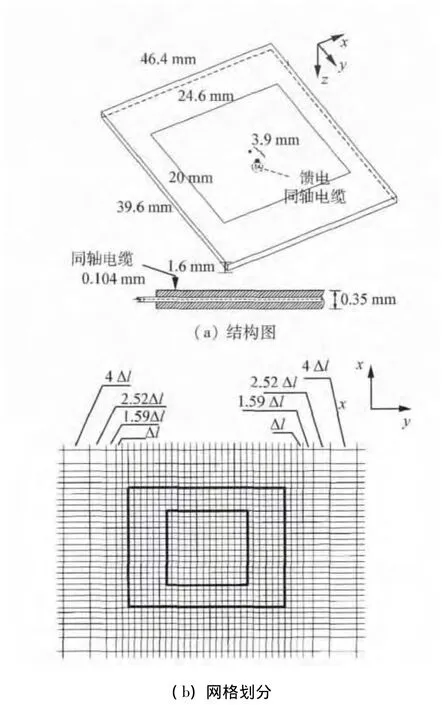
图4 微带天线结构和网格划分Fig.4 The geometry and FDTD grid of microstrip antenna

按上述方法进行建模后，利用本文的算法计算微带天线的回波损耗，并与有限元法(finite element method，FEM)、没有用奇异性处理技术的常规的FDTD算法及文献［11］算法的计算结果进行对比，如图5所示。

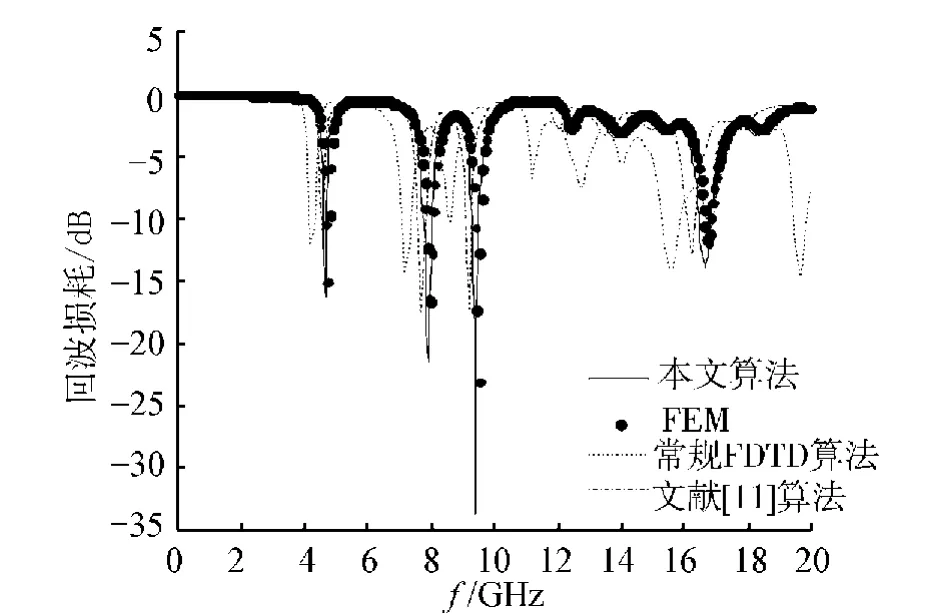
图5 微带天线的回波损耗Fig.5 Return loss of microstrip antenna

对比可见，常规的FDTD算法在整个频段的计算误差均较大;文献［11］的算法在5 GHz以下频段的精度较高，而在5 GHz以上频段随着频率增加，计算误差逐渐增大;而本文算法和FEM的计算结果在整个频段均保持较好的一致性，从而验证本文算法的可行性和计算精度。之后利用近远场变换得到了天线yoz面的远场方向图，如图6所示。由计算结果可见，天线的中心频率约为4.7 GHz，rEθ在θ=180o方向最大(θ为辐射方向与正z轴夹角，φ为辐射方向在xoy平面的投影与正x轴夹角)，可知天线极化方向与y轴一致。

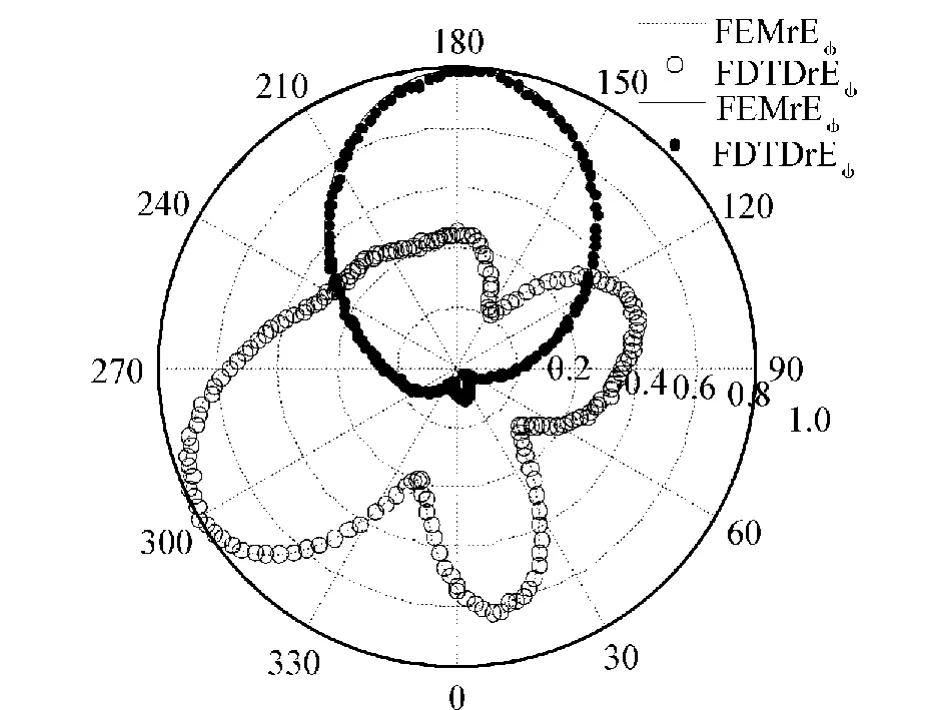
图6 微带天线的方向图Fig.6 Radiation pattern of microstrip antenna

3 电磁脉冲入射时的计算结果与分析

3.1 入射电磁脉冲描述

高功率电磁脉冲的电场可以用微分高斯脉冲近似，其数学表达式为

式中:E0=4.664×104V/m，t0=1.264×10-10s，τ=4.750×10-11s。其时域波形和频谱如图7。

采用上述电磁脉冲从不同角度入射，辐照目标天线，如图8所示，计算馈电同轴线中距离口径100Δl处的瞬态响应电压Ut，并通过傅里叶变换得到其频谱。其中θ为入射脉冲与正z轴夹角，φ为入射脉冲在xoy平面的投影与正x轴夹角，入射电磁脉冲采用平行极化波。

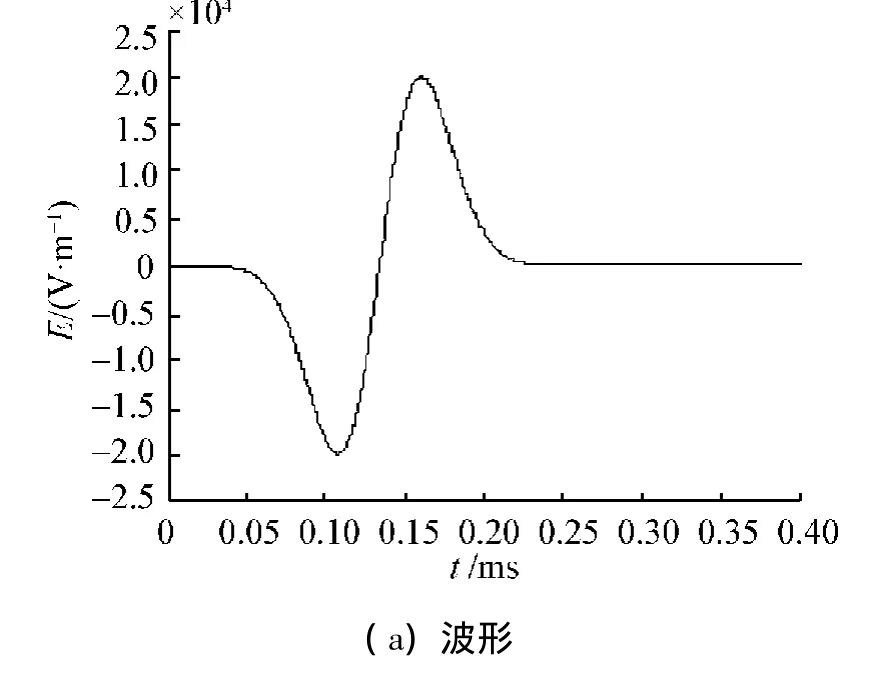
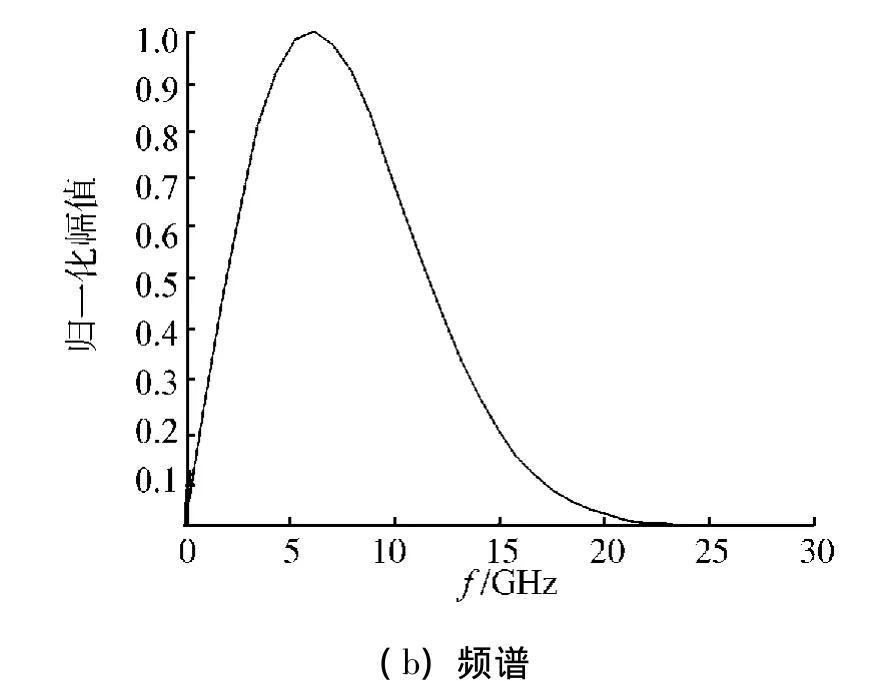
图7 入射脉冲的波形和频谱Fig.7 Waveform and spectrum of incident pulse

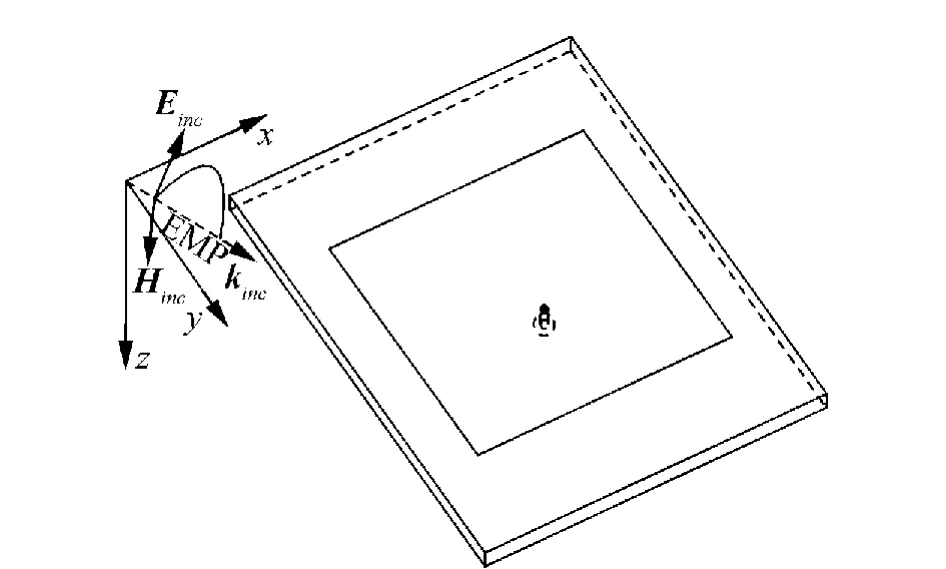
图8 电磁脉冲入射示意图Fig.8 Incidence of EMP

3.2 电磁脉冲沿不同φ入射时天线的响应

如图9(a)所示，高功率电磁脉冲分别沿着θ=π/4，不同的φ角入射，得到馈电同轴线中距离口径100Δl处的瞬态响应电压Ut的时域波形，由于微带天线的导体结构对电磁脉冲的反射作用，使得电磁脉冲在微带天线辐射片与接地板之间来回反弹产生了振荡，振荡的电磁场通过口径的耦合进入到馈电同轴线内，且随着能量的耗散，振荡幅度逐渐衰减。对比来看，φ=0时的响应电压峰值最高，约为8.7 V，φ=π/4时的响应电压峰值最低，约为6.3 V，这主要是由脉冲沿不同路径传播，导致微带天线中场的分布模式也不同引起的。

如图9(b)所示，高功率电磁脉冲分别沿着θ=π/4，不同的φ角入射，得到馈电同轴线中距离口径100Δl处的瞬态响应电压Ut的频谱，由图可见，φ=0时的响应电压主要集中在4、8、9.6 GHz等频段，由腔模理论可知［16］，其分别为相对于z轴的TM10、TM20和TM21(TMmn，m为x方向变化的半周期数，n为y方向变化的半周期数)等模式的谐振频率，由此可以得出，由于脉冲的激励使得微带天线中的电磁场存在上述分布模式。当脉冲沿φ=π/4入射时，与φ=0相比，响应电压频谱分布向低频转移，在4.7 GHz频段响应最大，其对应于该天线工作的主模TM01的谐振频率，此外在6.5、8、9.4 GHz频段的响应也较大，说明天线中存在较强的TM11、TM20和TM02等高次模。当脉冲沿φ=π/2入射时，频谱分布更集中于该天线主模TM01的谐振频率4.7 GHz频段，高次模频段的响应已相对较小。由此可见随着入射φ角的变化，天线中的电磁场模式分布也不同，由腔模理论分析可知，这主要是由于脉冲沿不同φ角入射时，脉冲沿不同的传播路径传播，等效于脉冲在不同尺寸的漏波空腔中传播造成的。

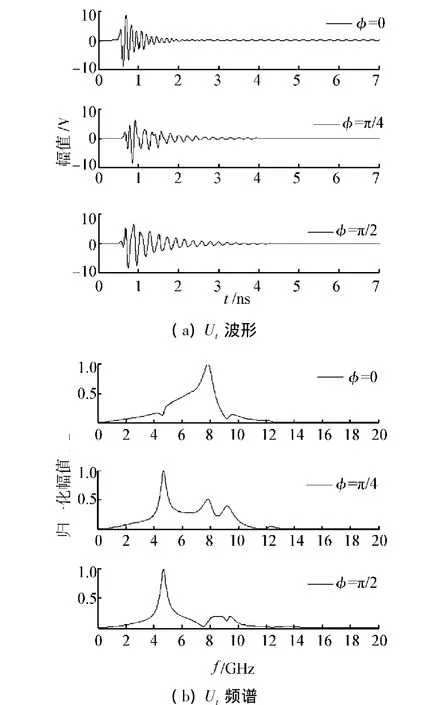
图9 脉冲沿θ=π/4，不同φ时的Ut波形和频谱Fig.9 Waveform and spectrum of Ut for differentφ ，but withθ=π/4

3.3 电磁脉冲沿不同θ入射时天线的响应

如图10(a)所示，高功率电磁脉冲分别沿着φ=π/2，不同的θ角入射，得到馈电同轴线中距离口径100Δl处的瞬态响应电压Ut的时域波形。由图可见，入射脉冲在微带天线内产生振荡，且振荡幅度逐渐衰减，其原因如前所述。对比来看，θ=0时的响应电压峰值最高，约为10.4 V，θ=π/2时的响应电压峰值最低，约为3.1 V。对照该天线的辐射方向图可知，当入射脉冲沿φ=π/2，θ=0方向入射时，天线接收效能最好，因而此时的天线响应电压最大。

如图10(b)所示，高功率电磁脉冲分别沿着φ=π/2，不同的θ角入射，得到馈电同轴线中距离口径100Δl处的瞬态响应电压Ut的频谱，由图可见，脉冲沿θ=0入射时，响应电压主要集中在4.7 GHz频段，这与天线主模TM01的谐振频率一致。当脉冲沿θ=π/4入射时，与 θ=0相比，在6.5、8、9.4 GHz频段的响应电压增大，说明由于脉冲的激励使得天线中出现了较强的TM11、TM20和 TM02等高次模。当脉冲沿θ=π/2入射时，与θ=0和π/4相比，6.5、8、9.4 GHz频段的响应电压不断增大，说明随着θ角增大，脉冲激励起的高次模也越强。造成上述现象的原因与上节类似。

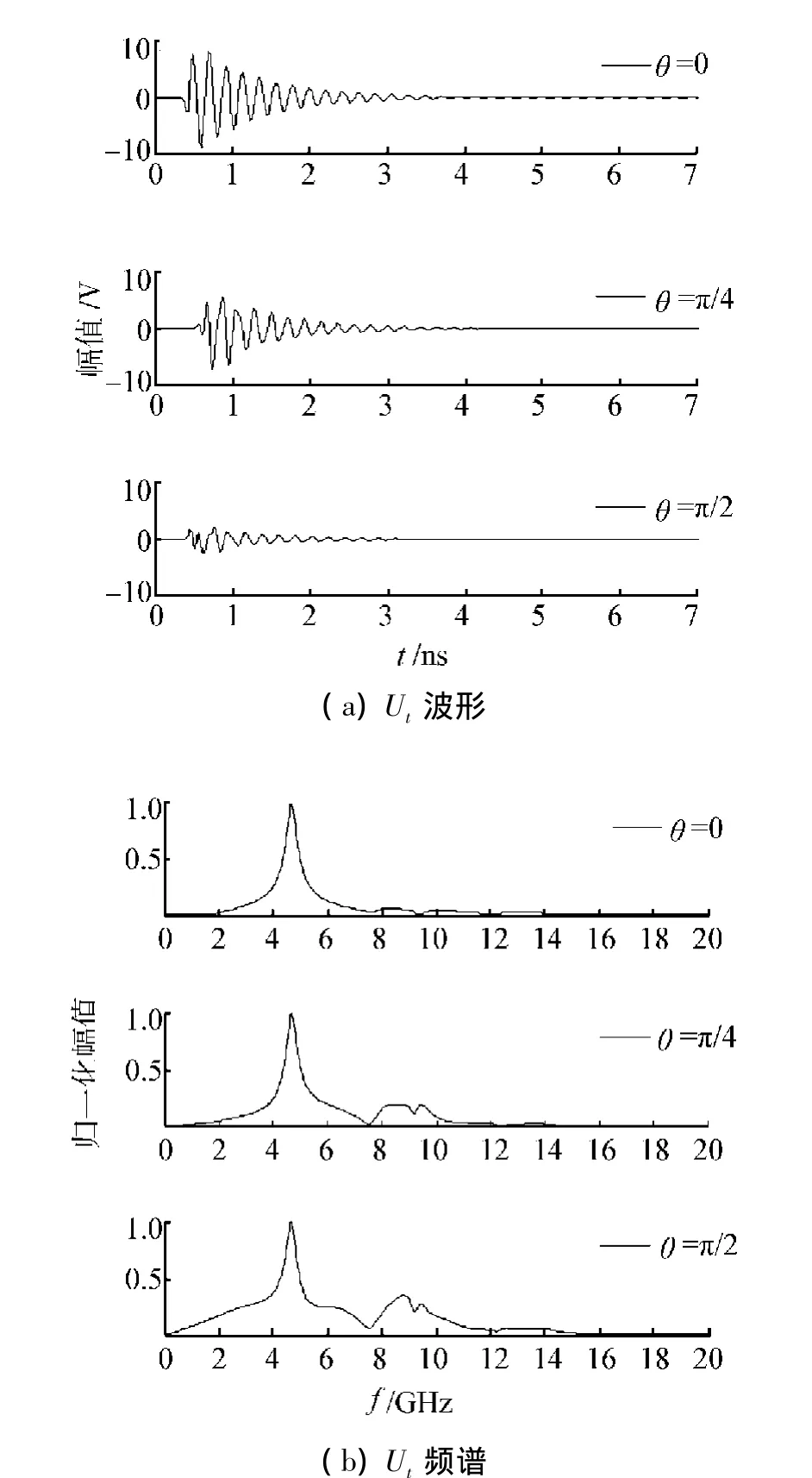
图10 脉冲沿φ=π/2，不同θ时的Ut波形和频谱Fig.10 W aveform and spectrum of Ut for differentθ，but withφ=π/2

4 结论

本文提出一种新的导体边缘奇异性处理技术，并利用该算法计算了同轴馈电微带天线在高功率电磁脉冲辐照下产生的瞬态响应。通过计算结果可以看出:

1)电场强度为20 kV/m的高功率电磁脉冲可在微带天线的同轴馈电线内产生最大幅值超过10 V的响应电压。

2)入射高功率脉冲在微带天线内不但激励起天线的主模 TM10，而且激励起 TM11、TM20、TM21和 TM02等高次模，这些高次模电磁场通过口径耦合使得同轴馈电线在一些频段也产生了的较大响应电压。

3)随着入射脉冲在xoy面的投影与正x轴夹角的增大，时域上，响应电压均小于10 V;频域上，高次模逐渐减小，其频谱分布更集中于天线主模TM01的谐振频率。

4)随着入射脉冲与正z轴夹角的增大，时域上，响应电压逐渐减小;频域上，高次模逐渐增大，其频谱分布逐渐分散于 TM11、TM20、TM21和 TM02等高次模对应的谐振频率频段。

［1］ZHANG Ka，SU Donglin，LIAO Yi，et al.Fast EMP response calculation of dipole antennas based on equivalent circuit［C］//10th International Symposium on Antennas，Propagation and EM Theory.Xi＇an，China，2012:1147-1149.

［2］LIN Jinyong，DONG Wenjie，ZHOU Chunmei.Investigation of injury effects to strong electromagnetic pulse on typical flying control system ［C］//2nd International Conference on Instrumentation and Measurement， Computer，Communication and Control.Guangzhou，China，2012:1532-1535.

［3］JIANG Zheng，YIN Wenyan，LIU Qifeng，et al.Transient responses of some antennas under the impact of an intentionally incident high-power electromagnetic pulse［J］.Progress in Electromagnetics Research，2010，105:365-381.

［4］王韶光，魏光辉，代平.超宽带电磁脉冲及其对电子装备的影响研究综述［J］.军械工程学院学报，2006，18(4):16-20.WANG Shaoguang，WEI Guanghui，DAIPing.Research of the impact of UWB electromagnetic pulse on electronic equipment［J］.Journal of Ordnance Engineering College，2006，18(4):16-20.

［5］CAMP M.Influence of the technology on the destruction effects of semiconductors by impact of EMP and UWB pulse［C］//Electromagnetic Compatibility Conference.Minneapolis，USA，2002，1:87-92.

［6］王泰春，贺云汉，王玉芝.电磁脉冲导论［M］.北京:国防工业出版社，2011:98-113.WANG Taichun，HE Yunhan，WANG Yuzhi.Introduction of electromagnetic pulse［M］.Beijing:National Defense Industry Press，2011:98-113.

［7］杨雨川.导体板上单极天线对电磁脉冲响应特性的矩量法分析［J］.强激光与粒子束，2008，20(4):649-652.YANG Yuchuan.Response characteristics and protection techniques of monopole on conductive plane exposed to electromagnetic pulse［J］.High Power Laser and Particle Beams，2008，20(4):649-652.

［8］STUTZMAN W L，THIELE G A.Antenna theory and design［M］.New York:John Wiley＆ Sons，1981:197-202.

［9］MUR G.The modeling of singularities in the finite-difference approximation of the time-domain electroma gneticfields equations［J］.Electromagnetic Compatibility，1981，23(1):377-382.

［10］TAFLOVE A.The finite-difference time-domain method［M］.Boston:Artech House，1995:63-89.

［11］RAILTON J，PAUL D L.Analysis of structures containing sharp oblique metal edges in FDTD using MAMPs［J］.IEEE Transactions on Antennas and Propagation，2010，58(9):2954-2959.

［12］TEIXEIRA F.Summary review on 25 years of progress and future challenges in FDTD and FETD techniques［J］.Applied Computational Electro magnetics Society Journal，2010，25(1):1-14.

［13］ABDULHUSSEIN N E.3-D FDTD design and analysis of a three-band composite microstrip patch antenna for wireless communication applications［C］//ICNIT.Gyeongju，Korea，2011:104-108.

［14］CHOID H，HOEFER.A graded mesh FDTD algorithm for eigenvalue problems［C］//IEEE MTT-S International Microwave Symposium Digest.Warsaw，Poland，1987，151(6):413-417.

［15］BLADEL JV.Singular electromagnetic fields and sources［M］.Oxford:IEEE Press，1991:125-158.

［16］LO Y T，SOLOMAN D.Theory and experiment onmicrostrip antenna［J］.IEEE Transactions on Antennas and Propagation，1979，27(2):137-145.