面向聚类分析的邻域拓扑势熵数据扰动方法
2014-10-25张冰杨静张健沛谢静
张冰,杨静,张健沛,谢静
(哈尔滨工程大学计算机科学与技术学院,黑龙江哈尔滨150001)
近年来,数据的隐私保护问题越来越被人们所关注[1-3]。如何保持隐藏数据的聚类可用性,即在隐私保护和聚类分析间寻求折衷,是目前研究的热点与难点之一。现有研究主要通过基于限制发布[4-5]和基于数据失真[6-7]2 种方式实现数据的隐私保护。基于限制发布的技术会弱化数据间的差异,切断元组间的关联或属性间的关联,基于数据失真的数据隐藏技术通过扰动实现数据的隐私保护,有利于数据特征的维持。通常采用数据失真的方式实现面向聚类分析的数据隐藏。为实现数据隐藏后的聚类可用性,文献[8]提出一种基于Fourier变换的数据扰动方法,保证数据扰动前后元组间的距离差值在一定范围内,以维持隐藏数据的聚类效用。文献[9]对初始数据集聚类并生成类标签,建立满足聚簇结构分布的匿名数据集,以实现隐藏数据的聚类可用性。以上面向聚类分析的数据隐私保护方法主要从保距和保分布2种角度实现数据隐藏后的聚类可用性,但这2种方法都无法较好地保护数据隐私安全并维持数据的可用性。2009年,倪巍伟等[10]提出了一种保邻域隐藏的思想,基于邻域属性熵维持数据集中节点的k邻域稳定性,实现保护数据集聚类质量和数据隐私安全的目的,但其仅处理数据点的邻域主属性值,具有较高的隐私泄露风险。
针对现有数据扰动方法不能较好地维持原始数据的聚类可用性问题,提出一种基于节点邻域拓扑势熵的数据扰动方法DPTPE,该方法将数据集中节点划分为不同类型,针对不同类型使用不同的隐私保护策略,能够有效地保持数据集的聚类效用和隐私安全。
1 相关概念
1.1 邻域拓扑势熵
数据发布中的隐私保护目的是破坏数据表中个体身份信息与敏感信息的关联,使攻击者无法获取个体的敏感信息。本文将具有d个准标识符属性的数据表T看做d维空间D,表T中的每条元组都可用D中的一个节点表示。下文将表T中的元组称为节点。
定义1 节点间的距离。节点p与q为d(d≥1)维空间D={A1,A2,…,Ad}中的任意2个节点,节点p与q在数值型属性Ai上的距离distAi(p,q)为distAi(p,q)=,节点p与q在分类型属性Aj上的距离distAj(p,q)定义为p与q在属性Aj上的层次距离[3],因此,节点p与q间的距离定义为

式中:pi和qi分别为节点p和q在属性Ai上的值。
定义2 p的k邻域半径。O为空间D的节点集合,p∈O,若存在o∈O且存在k个节点p'∈O(p'≠ p)满足 dist(p,p')≤ dist(p,o),并且至多有 k-1 个节点 p'∈ O,满足 dist(p,p')< dist(p,o),则节点p的k邻域半径k_rad(p)定义为
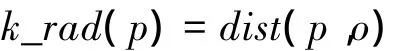
式中:dist(p,o)为节点p与o间的距离。
定义3 p的k邻域。p的k邻域Nk(p)为包含k个节点的集合,定义为
Nk(p)={p'∈ D,p'≠ p|dist(p,p')≤ k_rad(p)}式中:dist(p,p')为点p与p'间的距离,k_rad(p)为点p的k邻域半径。
图1显示了k=10时,二维空间D中点p的k邻域分布情况。
本文引入拓扑势场[11]的思想描述节点p的k邻域,将节点p的k邻域看作一个包含k个节点及其相互作用的拓扑势场,节点间拓扑势的大小反映了节点间相互作用的大小。
定义4 节点间拓扑势。p与q为d(d≥1)维空间D中的节点,节点p与q的拓扑势定义为

式中:mq为节点q的质量,dist(p,q)为节点p与q间的距离,影响因子σ>0为控制每个节点间相互作用的衰减速度与范围的参数。
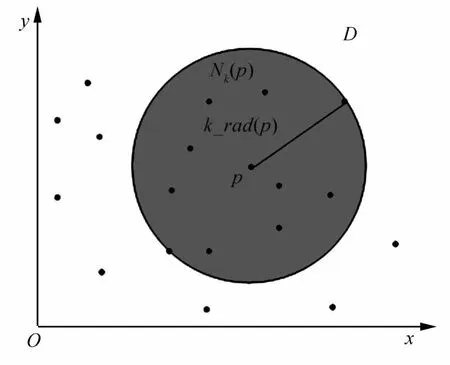
图1 空间D2中点p的k(k=10)邻域Fig.1 k(k=10)neighborhood of node p in space D2
本文假定空间D中的每个节点质量相同且为1。因此,∀p、q∈D,节点p与q间拓扑势φ(p,q) 为
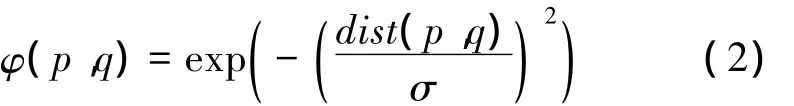
定义5 p的邻域拓扑势。p为d(d≥1)维空间D中的节点,q∈Nk(p),节点p的邻域拓扑势定义为
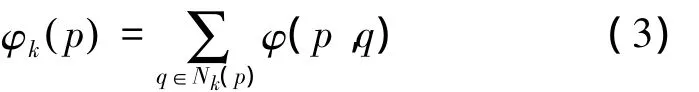
式中:Nk(p)为节点p的k邻域,φ(p,q)为节点p与q间的拓扑势。
定义6 p的邻域拓扑势熵。节点p为d(d≥1)维空间D中的一个节点,p的邻域拓扑势熵定义为

式中:φ(p,q)为节点p与q间的拓扑势,φkp()节点p的邻域拓扑势。
邻域拓扑势熵描述了节点p的k邻域内节点的分布情况。NTEk(p)值越大,节点p的k邻域内节点的差异性越大、分布越分散,p的k邻域内节点变化对p的k邻域组成的稳定性影响越小;反之亦然。
定理1 节点p的邻域拓扑势熵值不超过ln k。
证明:设q∈Nk(p),节点p与q在属性A上的拓扑势为φ(p,q),则根据定义6,有

因此,


推论1 节点p的邻域拓扑势熵值为NTEk(p),设pi(1≤i≤k)∈Nk(p),节点p与pi间的拓扑势为 φ ( p,pi),满足:
1)0≤NTEk(p)≤ln k;
2) 当 且 仅 当 φ(p,p1)= φ(p,p2)= …= φ(p,pk)=1/k时,NTEk(p)=ln k;
3)当且仅当∃i(1≤i≤k),使得φ(p,pi)=1且 ∀j≠i(1≤j≤k),都有φ(p,pj)=0 时,NTEk(p)=0。
2)由定理1及条件 φ(p,p1)=… =φ(p,pk)=1/k可知,NTEk(p)=-j
3)充分性:
由推论1的条件3)∃i(1≤i≤n),使得φ(p,pi)=1且 ∀j≠i,都有 φ(p,pj)=0及约定0ln0=0可知,NTEk(p)=- φ(p,pi)lnφ(p,pi)=0,即充分性成立。
必要性:当NTEk(p)=0时,如果∃i(1≤i≤n),使得φ(p,p)∉{0,1},则有 -
i> 0,因此NTEk(p)=-> 0,与NTEk(p)=0矛盾。该矛盾说明∀i(1≤i≤n),都有φ(p,pi)∈ {0,1},而由=1可知,∃i(1≤i≤n),使得φ(p,pi)=1且∀j≠i,都有φ(p,pj)=0,即必要性成立。
1.2 邻域分散度
定义7 邻域分散度。d(d≥1)维空间D中的节点p的k邻域为Nk(p),p在D中的邻域拓扑势熵值为NTEk(p),节点p在D中的邻域分散度定义为

邻域分散度描述了节点p与其k邻域中节点在邻域分散程度上的对比。如果节点p较其k邻域内节点在邻域分布上表现出较强分散性,那么节点p是邻域分散型节点;反之,节点p是邻域紧密型节点。
定义8 邻域分散型节点和邻域紧密型节点。d(d≥1)维空间D中的节点p的k邻域为Nk(p),如果节点p的邻域分散度Ndisk(p)>t,则节点p为邻域分散型节点;如果节点 p的邻域分散度Ndisk(p)≤t,则节点p为邻域紧密型节点。t为用户对节点类型划分的个性化设置,本文在试验中将t值设置为1。
性质1 邻域分散型节点的位置变化后,对其k邻域产生的影响要大于邻域紧密型节点位置变化后对其k邻域产生的影响。
证明:如图2所示,设p为邻域分散型节点,q为邻域紧密型节点,φk( p )=φk( q),节点p和q的k邻域半径相同且为r。根据p和q的邻域分散性,有NTEk(p)>NTEk(q)。由定义4可知,节点间距离越大,节点间拓扑势越小;由于∀t∈Nk(p),0<≤1及定义6节点拓扑势熵函数,可知∀t∈Nk(p),dis(p,t)越大,越大。因此,节点p的k邻域中大多节点呈远离p的趋势,节点q的k邻域中大多节点呈靠近q的趋势。由φk( p )=φk( q),在q的k邻域中必然存在少部分节点与q间距离近似于r。由于q的k邻域中部分节点距离q较近,部分与q间距离近似于r,因此,q在小范围内改变位置对其k邻域内节点的邻域影响较小;而p的k邻域中节点大多远离p,p的小范围位置变化也会对其k邻域中节点的邻域产生较大影响。因此,邻域分散型节点的位置变化后,对其k邻域产生的影响要大于邻域紧密型节点位置变化后对其k邻域产生的影响。

图2 不同类型节点示意图Fig.2 Schematic diagram of different types of nodes
2 数据扰动方法
本文提出一种面向聚类分析的数据扰动方法,通过分别对邻域分散型节点和邻域紧密型节点进行扰动,在尽量维持节点的邻域分布情况下,实现数据集的隐私保护。
2.1 邻域分散型节点的扰动方法
邻域分散型节点的邻域分散度高,相对邻域紧密型节点,邻域分散型节点位置的改变对其k邻域内节点的邻域稳定性影响较大。
性质2 若节点p为d(d≥1)维空间D中的邻域分散型节点,使用其k邻域中节点位置坐标的均值替代p,能够较好的维持p的k邻域稳定性。
证明:设d(d≥1)维空间D中的不同属性集合为{A1,A2,…,Ad},则节点 p的位置坐标可表示为(p1,p2,…,pd),则 ∀q ∈ Nk(p),p 与 q 间的距离差异可描述为dif(p,q)=
证毕。
根据性质2,本文使用邻域分散型节点的k邻域内节点位置坐标的均值代替其原始值,能够更好的维持邻域分散型节点的k邻域稳定性。
2.2 邻域紧密型节点的扰动方法
邻域紧密型节点的k邻域中节点分布相对紧密,且与其k邻域中节点间距离较近,邻域紧密型节点位置在小范围内改变对其k邻域影响较小。
文献[12]提出了安全邻域的概念,并证明了节点p和其替换节点p'间的距离|pp'|≤0.5(dist(p,pk+1)-dist(p,pk)),则在p的k邻域保持不变的情况下,使用p'替换p后能够保持p的k邻域的稳定性。据此,对于邻域紧密型节点,本文使用在安全邻域内随机选择一个节点替换其原始值,在保护节点的隐私安全同时,能够最大程度维持原始节点的k邻域稳定性。
设节点p在d维空间中的初始坐标为(p1,p2,…,pd),0 < r≤0.5(dist(p,pk+1)-dist(p,pk)),在p的安全邻域内随机选择一个节点p',可转化为求解方程组(p1-)2+(p2-)2+…+(pd-)2-r2=0的一组实数解。安全邻域内节点随机选取算法RSN的思想为:首先,随机选取d个和为r2的正实数(a1,a2,…,ad);然后,对于节点 p的每一维坐标值 pi,令(pi-)2=ai,即=pi±,即可得到pi的转换值。具体的算法如算法1所示。
算法1 安全邻域内节点随机选取算法RSN
输入:属性个数 d,节点 p,pk,pk+1
输出:p的扰动后坐标p'
算法步骤:
1)计算节点p的安全半径R=0.5(dist(p,pk+1)-dist(p,pk)),随机选择 r∈ (0,R];
2)随机选取d个和为r2的正实数(a1,a2,…,ad),对于d维空间中的每一维做如下操作:
①随机选择ai∈[0,r2);
②r2=r2-ai;
3)ad=r2
4)对于p的替换节点p'的每一维坐标做如下操作:

2.3 面向聚类分析的数据扰动算法
本文提出一种面向聚类分析的数据扰动方法,对不同类型节点实行不同扰动策略。算法的思想为:对于数据集中的每个节点,首先分析该节点的k邻域,并根据节点的邻域拓扑势熵判断节点的性质;如果该节点为邻域分散型,则使用其k邻域节点的均值替换该节点,如果该节点为邻域紧密型,则在其安全邻域中随机抽取一个节点替换该节点;最后,返回扰动后的数据。具体的算法如算法2所示。
算法2 基于节点邻域拓扑势熵的数据扰动算法DPTPE
输入:原始数据表T,属性个数d,邻域参数k
输出:扰动后的数据表T’
算法步骤:
1)计算表T中节点数目|T|,如果|T|<k,则返回重新设置k值;
2)对于表T中的每个节点做如下操作:
①获取p的k邻域点集Nk(p)及pk+1;
②计算p的邻域拓扑势熵;
③计算p的邻域分散度Ndisk(p);
④ 如果Ndisk(p)>1,则=qi;否则,执行算法 1,RSN(d,p,pk,pk+1);
3)返回扰动表T'。
算法的步骤1)进行初始化工作,假设表T的元组数目为n,则步骤1)判定k值的设置合理性,可在O(n)内完成。步骤2)为表T中节点坐标的替换,对每个节点首先获取节点的k邻域点集,至多需时间kO(n);然后计算节点的邻域拓扑势熵和邻域分散度,可在时间O(n)内完成;对于邻域分散型节点,使用其k邻域中节点分别在每个属性上的均值替换其原始值,需时间O(d),对于邻域紧密型节点,在安全邻域中随机选择一个节点代替其原始值,至多需时间O(d);因此步骤2)每扰动一个节点可在时间O(n)+O(d)内完成。步骤3)为扰动表T’的发布。由于k≪n且d为常数,因此,DPTPE算法可在时间O(n2)内实现数据表的扰动保护。
3 实验结果分析
实验采用UCI数据集中Forest fires、Magic gamma telescope和Poker hand 3个数据集作为本次实验数据,这些数据集被广泛应用于聚类分析的研究中。删除这3个数据集中存在缺省值的记录并去除分类型属性,3个数据集的具体描述如表1所示。

表1 数据集信息描述表Table 1 Data set information description
本实验从k邻域的稳定性和聚类的质量两方面进行分析,并将本文所提的 DPTPE算法与文献[13]中所提的RBT算法、文献[14]中所提 NeNDS算法进行比较。实验的运行环境为:硬件环境为Inter Pentium(R)4 CPU 3.00 GHz处理器,2.00 GB内存,Micros of tWindows XP操作系统,算法均在VC++6.0与Matlab 7.0混合编程环境下实现。
3.1 k邻域稳定性分析
本文使用k邻域稳定性系数度量节点p在数据扰动前后的k邻域稳定性,节点p的k邻域稳定系数定义为

数据表T的k邻域稳定系数定义为
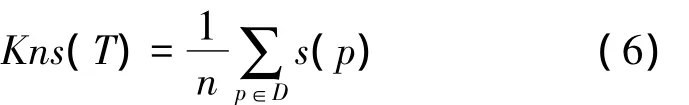
式中:T为原始数据表,T'为扰动后数据表,f(p)为应用到T上的扰动函数,Nk(p)为节点p的k邻域。
表2给出了3种算法的k邻域稳定性比较。表2可知使用DPTPE算法扰动后数据表的k邻域稳定性近似于RBT算法且高于NeNDS算法。由于RBT算法基于矩阵变换以保持数据扰动前后元组间的距离,维持节点k邻域稳定性能力最强;DPTPE算法基于节点邻域拓扑势熵确定节点类型并应用相应扰动策略,也能够较好的维持节点k邻域稳定性,;而NeNDS算法将表中元组分组并进行组内扰动,维持节点k邻域稳定性的能力最弱。

表2 3种算法的k邻域稳定性比较Table 2 Comparison of k neighborhood stability between three algorithms
3.2 聚类质量分析
F-measure[9]是衡量数据隐藏后聚类可用性的常用指标。对原始数据集和扰动数据集应用某种聚类算法,获得的F-measure值越大,扰动算法维持数据聚类可用性的能力越强。分别使用DPTPE算法、RBT算法和NeNDS算法对3个数据集进行扰动处理,对扰动前后的数据集使用k-means算法和DBScan算法聚类并比较所得的F-measure值。
图3~5分别给出了3种算法在不同数据集上的F-measure值对比。图中可知DPTPE算法的F-measure值最高,RBT算法与 DPTPE算法的 F-measure值相近,NeNDS算法的F-measure值最低。这是由于RBT算法能够在数据隐藏后近似保持元组间距离;NeNDS算法通过割裂属性间关联以维持每个属性分组内的数据分布,但缺乏对数据集中多维属性上分布特征的维持;而DPTPE算法对不同类型节点应用不同的扰动策略,在数据隐藏的同时,能够较好地维持聚类的可用性。
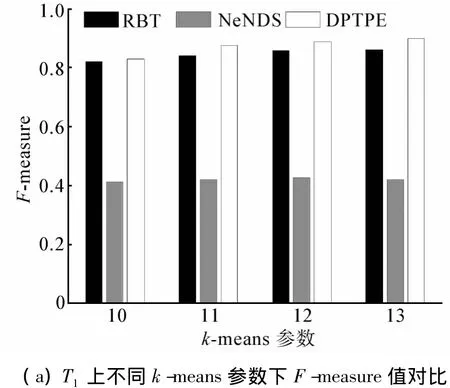

图3 T1上F-measure值对比Fig.3 Comparison of F-measure values in dataset T1

图4 T2上F-measure值对比Fig.4 Comparison of F-measure values in dataset T2

图5 T3上F-measure值对比Fig.5 Comparison of F-measure values in dataset T3
4 结束语
本文提出一种基于邻域拓扑势熵的节点分类方法,对不同类型节点应用不同的扰动策略,实现了隐藏数据的聚类可用性。实验结果表明,该方法能够有效地保持数据的隐私安全和聚类的效果。下一步的工作将优化节点间距离度量的方法和节点类型划分方法,更好地实现数据隐私保护和聚类可用性间的平衡。
[1]FUNG B CM,WANG K,CHEN R,et al.Privacy-preserving data publishing:a survey of recent developments[J].ACM Comput Surv,2010,42(4):1-53.
[2]杨高明,杨静,张健沛.半监督聚类的匿名数据发布[J].哈尔滨工程大学学报,2011,32(11):1489-1494.YANG Gaoming,YANG Jing,ZHANG Jianpei.Semi-supervised clustering-based anonymous data publishing[J].Journal of Harbin Engineering University,2011,32(11):1489-1494.
[3]王智慧,许俭,汪卫,等.一种基于聚类的数据匿名方法[J].软件学报,2010,21(4):680-693.WANG Zhihui,XU Jian,WANG Wei,et al.Clusteringbased approach for data anonymization[J].Journal of S of tware,2010,21(4):680-693.
[4]MACHANAVAJJHALA A,KIFER D,GEHRKE J,et al.L-diversity:privacy beyond k-anonymity[J].ACM Transactions on Knowledge Discovery from Data,2007,1(1):1-52.
[5]WONG R,LIJ,FU A,et al.(α,k)-anonymous data publishing[J].Journal of Intelligent Information Systems,2009,33(2):209-234.
[6]PARAMESWARAN R,BLOUGH D M.Privacy preserving data obfuscation for inherently clustered data[J].Journal of Information and Computer Security,2008,2(1):1744-1765.
[7]倪巍伟,陈耿,崇志宏,等.面向聚类的数据隐藏发布研究[J].计算机研究与发展,2012,49(5):1095-1104.NIWeiwei,CHEN Geng,CHONG Zhihong,et al.Privacypreserving data publishing for clustering[J].Journal of Computer Research and Development,2012,49(5):1095-1104.
[8]MUKHERJEE S,CHEN Z Y,GANGOPADHYAY A.A privacy-preserving technique for Euclidean distance-based mining algorithms using Fourier-related transforms[J].Journal on Very Large Data Bases,2006,15(4):293-315.
[9]FUNG B CM,WANG K,WANG L Y,et al.Privacy-preserving data publishing for cluster analysis[J].Data &Knowledge Engineering,2009,68(6):552-575.
[10]倪巍伟,徐立臻,崇志宏,等.基于邻域属性熵的隐私保护数据干扰方法[J].计算机研究与发展,2009,46(3):498-504.NIWeiwei,XU Lizhen,CHONG Zhihong,et al.A privacy preserving data perturbation algorithm based on neighborhood entropy[J].Journal of Computer Research and Development,2009,46(3):498-504.
[11]淦文燕,赫南,李德毅,等.一种基于拓扑势的网络社区发现方法[J].软件学报,2009,20(8):2241-2254.GANWenyan,HE Nan,LIDeyi,et al.Community discovery method in networks based on topological potential[J].Journal of S of tware,2009,20(8):2241-2254.
[12]倪巍伟,张勇,黄茂峰,等.一种向量等价置换隐私保护数据干扰方法[J].软件学报,2012,23(12):3198-3208.NIWeiwei,ZHANG Yong,HUANG Maofeng,et al.Vector equivalent replacing based privacy-preserving perturbing method[J].Journal of Software,2012,23(12):3198-3208.
[13]OLIVEIRA SRM,ZAIANEO R.Achieving privacy preservation when sharing data for clustering[C]//Proceedings of the 2004 SDM Conference.Toronto,Canada,2004:67-82.
[14]RUPA P,DOUGLASM B.Privacy preserving data obfuscation for inherently clustered data[J].International Journal of Information and Computer Security,2008,2(1):1744-1765.
