多管火箭弹射击精度的复合形法优化
2014-08-23王巍陈卫东张宝财吴限德路胜卓于佳
王巍,陈卫东,张宝财,吴限德,路胜卓,于佳
(哈尔滨工程大学航天与建筑工程学院,黑龙江哈尔滨150001)
多管火箭武器以其射击距离远、覆盖面大、成本低廉和作战效费比高等特点成为国内外研究的重点。多管火箭弹箭体间相对距离较近、多枚火箭弹处于同一发射平台、相互间干扰严重,导致每枚火箭弹起始扰动随机性较大[1-2],落点散布成为制约其性能的主要问题。因此,对火箭弹的射序和射击间隔进行调整和优化,以期最大限度减小起始扰动对落点散布的影响,以达到提高射击精度的目的。射击密集度是多管火箭武器系统主要的作战性能指标之一,发射动力学理论与大量试验证明,弹箭起始扰动是影响武器系统射击密集度的主要因素之一,弹箭起始扰动取决于武器发射系统总体结构、发射环境(如地面工况)及射击间隔和发射顺序设计。
本文在不改变武器发射系统总体结构、发射环境的前提下,采用复合形优化算法,以射击时间间隔和发射顺序为设计变量,建立了多管火箭弹射击密集度优化模型,优化得到现有的约束条件下最佳射击时间间隔和顺序,提高多管火箭弹射击密集度。
1 影响射击密集度的因素
射击密集度是多管火箭弹的一个重要效能指标,表征弹着点对于平均弹着点的密集程度,通常用其中间误差E表示。影响射击计密集度的主要因素包括多管火箭弹的各种随机因素和武器系统的固有力学特性。前者是无法预先确定的,如阵风、起始扰动、推力偏心、质量分布不均衡等;后者是可以预先确定的,如弹炮相互作用、火箭弹的装填位置、射序等。对非随机性扰动因素的影响可以用弹道修正理论进行修正,而对随机性扰动因素的影响,则无法修正。
在外弹道学中,如果火箭弹在标准条件下作无扰动飞行,其弹道是确定曲线,称为理想弹道。在理想弹道方程组中,没有考虑的干扰因素称为扰动因素[3]。这些扰动因素是受扰动后的实际弹道诸元与理想弹道诸元之间产生偏差。火箭弹起始扰动指弹丸外弹道方程起始条件对应的相关起始参量,作为6自由度刚体的弹丸方程有12个起始参量,即转动角、速度角、线位移、线速度各3个。起始扰动包括起始摆动角 Φ0、起始摆动角速度、起始偏角Ψ0及其角速度以及起始线位移r0、线速度、自转角γ0和自转角速度。起始扰动作为火箭弹自由飞行阶段的起始条件,是影响射弹散布的一个主要原因。火箭弹起始扰动是在发射过程中弹、炮、药、环境等因素综合影响的结果。任何火箭炮的动态特性对于射击密集度的影响,都必须通过火箭弹起始扰动来反映。
发射动力学理论与大量试验证明,弹箭起始扰动是影响武器系统射击密集度的主要因素之一,弹箭起始扰动取决于武器发射系统总体结构、发射环境(如地面工况)及发射顺序和射击间隔设计,不同的地面刚度引起多管火箭弹系统振动特性不同,不同的振动特性直接影响着多管火箭弹的射击密集度;多管火箭弹作为连射武器,射序和射击间隔对多管火箭弹射击密集度的影响非常大,这是因为同一门多管火箭弹在不同射序和射击间隔发射时引起多管火箭弹系统的质量分布和刚度分布等参数不同,从而引起其振动特性不同,每一发火箭弹的发射初始条件亦不同,射击频率与固有振动频率、弹炮相互作用的位置及时间的匹配关系对其动态性能的影响非常突出。
2 射序和射击间隔优化方案
多管火箭弹最佳射序和射击间隔优化设计方案由3部分组成,分别是优化算法、外弹道模型和迭代仿真求解。其中,优化算法包括射序优化算法、射击间隔优化算法和同时考虑射序和射击间隔的优化算法;迭代仿真包括仿真结果分析和根据精度的设计变量更新策略。射序和射击间隔优化设计方案如图1所示,时间约束、射击顺序约束、平台约束和其他约束共同组成射击约束。

图1 射序和射击间隔优化设计方案Fig.1 Fire sequence and interval optimization scheme
3 射序和射击间隔优化算法
3.1 优化模型的建立
最优化问题一般可表示为如下标准形式

式中:f(X)称为目标函数,用它来评价一个设计方案好坏的具体数值评判标准;gi(X)≤0(i=1,2,…,m)称为不等式约束条件,m为不等式约束条件的个数;hj(X)≤0(j=1,2,…,l)称为等式约束条件,l等式约束条件的个数。
对于多管火箭弹密集度优化问题,若建立优化模型,则需要以下3个条件:1)可以更快更好的求解问题的优化算法;2)能够评价多管火箭弹密集度大小的目标函数;3)符合实际要求的约束条件。
3.2 目标函数建立
根据前面所述多管火箭弹射击密集度优化问题的特点,目标函数为离散函数,没有具体的数学表达式,只可以通过计算,得到函数值的信息。而目标函数值,多管火箭弹射击密集度表征弹着点对于平均弹着点的密集程度,通常用弹着点的中间误差E表示,可以通过下式计算:

式中:EX和EZ表示多管火箭弹的纵向和横向密集度;n为射击次数;为火箭弹的纵向和横向平均落点。
如前面所述,影响射击密集度的主要因素包括多管火箭弹的各种随机因素和武器系统的固有力学特性。前者是随机的,不可预测,也不能够改变;后者是确定性的,可以通过改变系统参数来提高密集度,其对射击密集度的影响,必须通过火箭弹起始扰动来反映,起始扰动是影响武器系统射击密集度的主要因素之一。
对于多管火箭弹的密集度优化问题,可以把影响密集度的主要因素起始扰动作为设计变量,其中起始扰动可抽象成12个参量,这些参量受弹炮结构、射击间隔和射击顺序共同影响。即:弹炮起始扰动取决于武器发射系统总体结构、发射环境(如地面工况)及发射顺序和射击间隔。鉴于对原有发射系统的兼容性,此处要求不改变武器发射系统总体结构,同时还应适应各种作战环境,所以通过设计射击时间和顺序,来提高多管火箭弹密集度。
传统多管火箭弹的发射方式是,以一定射序、固定的射击间隔发射,但是这种发射顺序和射击间隔不是最优的。本文的目的是求解出最佳的发射顺序和射击间隔,与传统发射方式不同的是,本文所寻求的射击间隔不是固定的,而是可变的,每发火箭弹的射击时间差都可能是不同的,所以提出一种数组变量表示方法,可以将射击时间和发射顺序表示在一个变量里。
射击时间和发射顺序两个变量,前者是连续的,而后者是离散的,在一个目标函数中出现这样两个变量,使问题变得复杂,对于40管火箭来说,2个变量都是40维的,优化问题维数过高,便会增加求解问题的难度,为了解决这一问题,本文提出一种新的数组变量 X=(t1,t2,…,t40),其中,ti(i=1,2,…,40)表示第i号火箭弹的射击时间,而非射击间隔。火箭弹的编号原则遵循原有的发射顺序,而非射击间隔,如图2所示,为某火箭武器的发射顺序和装填位置,根据火箭弹原有的发射顺序进行排序,记为(1,2,…,40)。这里,火箭弹的编号指的并不是按照2的发射顺序进行发射,而是以此发射顺序为基础,寻求比之更优的发射顺序。若i=5,则表示编号为5的火箭弹的射击时间,而它的发射顺序可以按照所有火箭弹的射击时间排序来表示,所有ti(i=1,2,…,40)从小到大排列,若t5排在第10位,则表示编号为5的火箭弹的射序是10。所以X=(t1,t2,…,t40)既可以表示射击时间,又可以表示射序,将连续变量和离散变量统一结合起来,大大的简化了优化问题的复杂程度,使问题更易于求解。

图2 40管火箭武器的发射顺序和装填位置Fig.2 40-tube rocket firing sequence and load position
那么多管火箭弹密集度优化问题的目标函数可以建立为

式中:X是表示射击时间和顺序的变量,为一数组X=(t1,t2,…,t40),C 为影响密集度的其他量,为确定量。这里没有考虑随机因素的影响,因为在确定性因素影响下的最优解是考虑随机性因素最优解的必要解,所以不考虑随机因素影响的最优解也具有重要的意义。
3.3 约束条件确定与优化模型
多管火箭弹密集度优化问题,其设计变量为射击时间和射序,按照火箭弹的发射要求,同一时刻不能同时发射2枚或2枚以上火箭弹,而是逐一的发射,即发射顺序是 (1,2,…,40)。而且火箭弹的射击间隔,不能过长,也不能过短,必须限制在一定时间内。多管火箭弹的一个重要的战术特点就是在短时间内形成强大火力密度,所以射击间隔过长,就失去了这一战术特点,那么多管火箭弹就和单管火箭没有太大区别了。射击间隔不能过短的原因是,考虑到发射频率与武器系统的固有振动频率的匹配关系对其动态性能的影响非常突出,和前一发火箭弹尾焰对空气的扰动对后一发火箭弹的弹道影响。
现行40管火箭射击间隔为0.5 s,一轮齐射时间为20 s,为得到最优解将齐射时间放宽为40 s。对于 X=(t1,t2,…,t40),其满足的条件是:

多管火箭弹密集度优化模型建立如下:

式中:X是表示射击时间和顺序的变量,为一数组X=(t1,t2,…,t40),C 为影响密集度的其他量,为确定量。
3.4 复合形计算过程
复合形法求解约束最优化问题的一种直接算法,是无约束最优化问题的单纯形法的推广。它只适用于只有不等式约束的最优化问题,使用该法仅需比较目标函数值即可决定搜索方向,算法较简单,对目标函数的要求不苛刻。

用单纯形法求解约束最优化问题,在处理约束条件时会出现一些困难。当向边界调优时,单纯形容易退化降维,当反射点XR≈XC时,产生降维现象,就不能求得优化问题的最优解。复合形法是以n1个初始点为顶点构成一个不规则多面体,为防止退化降维现象,复合形多面体顶点个数n1要大于n+1,一般n+1<n1≤2n。
复合形法寻优方法主要工作是生成初始复合形和更新复合形。复合形法的基本思想是:在可行域内构造初始复合形,然后通过比较各顶点目标函数值,在可行域中找一个目标函数值有所改善的新点,并用其替换目标函数值较差的顶点,构成新的复合形。不断重复上述过程,复合形不断变形、转移、缩小,逐渐地逼近最优点。当复合形各顶点目标函数值相差不大或者各顶点相距很近时,则目标函数值最小的顶点即可作为最优点。为了减小计算变量,复合形法在寻优过程中一般只以在可行域内的反射作为基本搜索策略。
综合来说复合形法的算法思路清晰,容易掌握;不需要导数,不需作一维搜索,对函数形态没有特殊要求;程序结构简单,计算量不大;对初始点要求低,能较快地找到最优解,算法较为可靠。求解时需给出变量取值区间及初始复合形;随着变量维数增多计算效率明显降低;对约束条件较多的非凸问题,常出现多次向形心收缩,使收敛速度减慢。
复合形法的目标函数:

n个常量约束条件:ai≤xij≤bii=1,2,…,n。
k个函数约束条件:

复合形法的主要步骤如下:
1)初始复合形2n个顶点的产生
给定满足约束条件的第一个顶点坐标:

在n维变量空间中,确定出初始复合形其余2n-1个顶点,其方法如下:
按常量约束条件产生第j个顶点,Xj中分量值xij(i=1,2,...,n)为
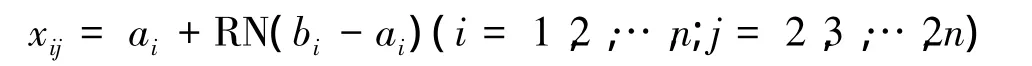
其中:RN是[0,1]之间的伪随机数。
显然,由上述方法产生的初始复合形的各顶点满足常量约束条件,在检查它们是否满足函数约束条件,如果不符合,则做出调整,直到全部满足方可,其原则是:
假设前j个点已满足所有约束条件,而第j+1个点不满足约束条件,则作如下调整变换:
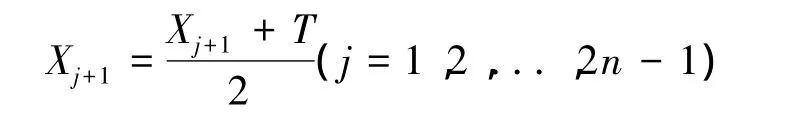
式中:T是前j个点的形心,表示为:

此过程一直到满足约束条件为止。
初始复合形的2n个顶点确定以后,计算各顶点的目标函数值:
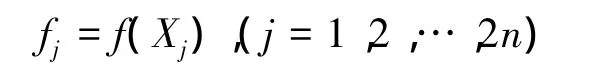
2)求最坏点XR和次坏点XG

3)计算最坏点XR的反射点XT
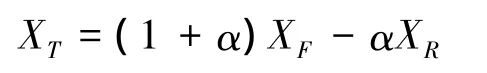
式中:XF为去掉最坏点的其余点的形心XF=为大于零的反射系数,一般取α=1.3。
4)确定一个新的顶点代替最坏点XR构成新的复合形。其方法如下:
如果f(XT)>fG,则用下式修改XT:

直到f(XT)≤fG为止。
然后检查XT是否满足所有约束条件。如果某个分量XT(j)不满足常量约束条件,即如果XT(j)<aj或XT(j)>bj,则另XT(j)<aj+δ或δ为很小的常量,一般取δ=10-8,然后重复4)。
如果XT不满足函数约束条件,则用下式修改XT:

重复4),直到f(XT)≤fG且XT满足所有约束条件为止。此时,令
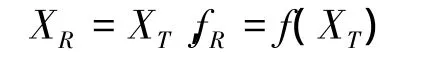
重复2)~4),直到复合形中各顶点距离小于预先给定的精度要求为止。
4 优化结果
仿真和试验数据参考文献[7],以40 s内,40管火箭齐射为例,经过复合形法优化,能够得到纵向最优密集度,即弹着点中间误差EX为

横向最优密集度,即弹着点中间误差EZ为

多管火箭射击密集度最优结果,中间误差E为

表示火箭弹发射顺序和激发时间的最佳设计变量(单位:s)为

最佳设计变量对应的射击顺序和装填位置关系如图3所示,每管火箭弹由3组数字表示,第1行数字表示优化后的射击顺序,第2行数字分别表示自左至右的排列顺序和行列顺序。

图3 优化后射击顺序和装填位置Fig.3 The firing order and load position after the optimization
图4给出了40管火箭弹射序和射击间隔优化过程的收敛情况,在不考虑随机因素的情况下,中间误差在450次迭代后达到最小。

图4 优化收敛过程Fig.4 The optimization progress
图5给出了多管火箭弹分别按照优化射序与射击间隔和传统射击方式的落点分布情况,从图中可以看出,优化后的火力密集明显优于传统射序和射击间隔时的火力密集度。
5 结束语
通过复合形法对多管火箭弹射击间隔和射序优化,确定了典型多管火箭弹在给定的约束条件下最佳射序和射击间隔。通过模拟打靶方式,验证了优化射序对射击密集度的改善效果,落点集中在500 m半径区域内。为形成小起始扰动多管火箭弹精度总体设计通用方法提供优化方法和典型优化设计方案。
[1]鲜勇,张毅.制导工具误差对导弹射击精度的影响分析[J].飞行力学,1999,17(2):82-86.XIAN Yong,ZHANG Yi.Analysis on effect of a missile's guidance instrument error on fire accuracy[J].flight dynamics,1999,17(2):82-86.
[2]周全,曲玉琨.远程火箭弹射击效力研究[J].弹箭与制导学报,2010,30(4):101-103.ZHOU Quan,QU Yukun.Research on the fire effectiveness of long range rocket projectile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(4):101-103.
[3]倪庆华,曲玉琨,孙剑锋.气象条件对远程火箭炮射击精度的影响及对策[J].指挥控制与仿真,2009,31(6):104-107.NI Qinghua,QU Yukun,SUN Jianfeng.Influence and countermeasure of meteorology condition for shooting precision of certain type of long-range rocket launcher[J].Command Control& Simulation,2009,31(6):104-107.
[4]张中利,于存贵,马大为,等.火箭弹在定向管内碰撞运动的仿真研究[J].系统仿真学报,2007,19(4):875-878.ZHANG Zhongli,YU Cungui,MA Dawei,et al.Simulation study of impact movement of rocket projectile in direction pipe[J].JournalofSystem Simulation, 2007,19(4):875-878.
[5]张驰,芮筱亭,戎保,等.机载多管火箭非满管射击试验方法研究[J].振动与冲击,2013,32(2):1-5.ZHANG Chi,RUI Xiaoting,RONG Bao,et al.Test method of non-full loading firing dispersion for an airborne multiple launch rocket system[J].Journal of Vibration and Shock,2013,32(2):1-5.
[6]戎保,芮筱亭,王国平,等.参数不确定性细长火箭弹随机特征值问题研究[J].工程力学,2012,29(7):341-346.RONG Bao,RUI Xiaoting,WANG Guoping,et al.Study on random eigenvalue problems of slender rocket with uncertain parameters[J].Engineering Mechanics,2012,29(7):341-346.
[7]芮筱亭.多管火箭发射动力学仿真与试验测试方法[M].北京:国防工业出版社,2003:97-124.
