集成模型ARIMAX-GARCH及其在股票预测中的应用

沈小欣 赵亚玲 朱海江

(浙江师范大学 数理信息学院，浙江 金华321004)

集成模型ARIMAX-GARCH及其在股票预测中的应用

沈小欣 赵亚玲 朱海江

(浙江师范大学 数理信息学院，浙江 金华321004)

在分析ARIMAX模型与GARCH模型的预测特性和优劣的基础上,建立了基于两者集成的ARIMAX-GARCH模型，其基本思想是充分发挥两种模型在回归与序列波动性因素提取方面的优势.对从5大行业中随机抽取的10只只股票的实证分析表明，该集成模型在股票预测中的准确率与稳定性显著优于两个单一模型.

时间序列；ARIMAX模型；GARCH模型；ARIMAX-GARCH模型；股票预测

近几十年来,很多学者开始利用时间序列模型研究数据的变化规律.1976年George E.P.Box和Gwilym M.Jenkins在研究CO2的输出浓度时开始运用多元时间序列分析方法[1]，这就是早期的ARIMAX模型.1987年Engle和Granger又提出协整的概念[2]，进一步完善了ARIMAX模型.ARIMAX模型并没有广泛运用于金融时间序列，其原因是很多金融时间序列的残差序列具有异方差性，而ARIMAX模型并不能很好地刻画金融时间序列的波动性.1982年Engle提出了条件异方差模型[3]，Bollerslevb于1986对文献[3]的模型作了修正[4]，提出广义自回归条件异方差模型，即GARCH模型.我国学者唐齐鸣与陈健利用ARCH模型对中国股市的波动性进行了检验,发现其具有较明显的ARCH效应[5].

股票预测一直是经济统计的一个热点.常用的股票预测模型中均使用股票收盘价这一单一变量，然而华尔街有句名言，“价走量先行”，说明股票价格与成交量之间有一种必然的联系，故比较好的股票预测模型应该包含收盘价和成交量这两个指标，因而是一个多元时间序列模型，且其具有金融时间序列的异方差性，故前面介绍的几种模型都不能很好地适用于股票预测.通过分析，本文将建立由ARIMAX模型和GARCH模型集成的ARIMAX-GARCH模型，该集成模型的主要思想是加入交易率序列为输入变量序列，建立多元时间序列模型(ARIMAX)来拟合回归部分，再利用GARCH模型提取残差序列中的异方差因素，最后利用集成模型进行股票预测.

1 ARIMAX-GARCH模型

集成模型的具体表达式如下：

2 实证分析

我们随机抽取中国5大行业中的10只股票作为研究对象，由于历史数据获取有限，故10只股票的截取时间并不能达成一致.其中洋河股份截取时间自2010-07-13至2013-11-07，汤臣倍健截取时间自2011-05-25至2013-11-07，其余8只股票数据的截取时间均为自2006-02-06至2013-12-06，数据来源于雅虎财经网站.

本文以洋河股份(002304)为例，首先详细介绍了采用3种模型建模的过程及Eviews[6]实现；其次分别预测现有样本数据中最后7天的收盘价；最后采用均方根误差和平均绝对百分比误差这两个指标对3种模型的预测结果进行比较.其余9只股票的具体建模过程省略，10只股票的预测结果将在后文呈现.

2.1数据整理

为方便论述，记上述时期日收盘价序列为C，日交易量序列为V，时间序列中的时间点编号为1到797.首先来看洋河股份(002304)收盘价和交易量的时序图，见图1.

很明显，收盘价C和日交易量V都为不平稳的时间序列，我们定义序列C的收益率为：

RCi+1=100(lnCi+1-lnCi)，

相应地，定义交易率为

RVi+1=100(lnVi+1-lnVi).

2.2平稳性检验

对序列RC和序列RV做单位根检验(ADF检验)，结果表明在3种显著性水平下都拒绝原假设，故可认为序列RC和序列RV都平稳.

2.3 3种模型参数估计以及预测效果比较

2.3.1 ARIMAX模型

由交易率与收益率的相关性图及响应序列(收益率序列)的自相关性与偏相关性图可初步选出4个较优化的模型，为了进一步选出最优模型，借助Eviews软件，对这4个模型进行分析，见表1.

表1 4个模型的R2和定阶值(AIC)的比较

根据最小信息准则(AIC)，最终确定的模型为ARIMAX((5,6,7),0,(7)).

2．3.2 GARCH模型

在给GARCH模型定阶时，可供选择的有如下两个模型：

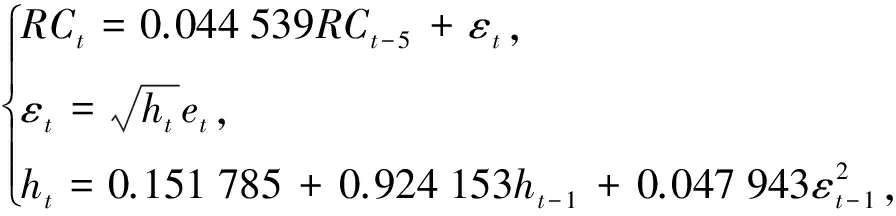
为了选出最优模型，根据最小信息准则(AIC)，对这两个模型进行分析，计算它们的定阶值(AIC).计算结果如下：模型一的定阶值为4.467 908，模型二的定阶值为4.468 258.因此最终确定模型一为最优模型.

2.3．3 ARIMAX-GARCH模型

ARIMAX-GARCH集成模型参数拟合后如下式：

对此时的残差做ARCH-LM检验[6]，结果显示残差不再具有ARCH效应.

2.3．4 3种模型预测效果的比较

为了更加全面地描述3个模型对股票的预测效果，本文采用均方根误差(RMSE)和平均绝对百分比误差(MAPE)两个指标来衡量模型预测效果的好坏(第一个指标是绝对指标，第二个指标是相对指标)[7].两个指标分别定义为：

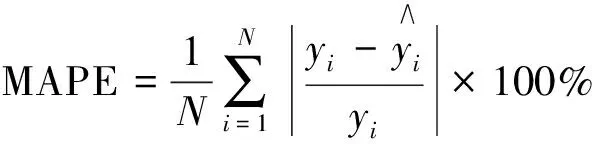
表2 各模型预测效果比较

如表2所示，以上10只股票中有6只显示ARIMAX-GARCH模型的预测误差明显小于其它两个模型，而表明其他两个模型预测效果较优的分别有两只股票.仔细观察发现，在ARIMAX模型预测效果最好的两只股票中，GARCH模型的预测效果最差，且差距很大，而在GARCH模型预测效果最好的两只股票中，ARIMAX模型的预测效果最差，这充分说明两个单一模型的预测效果不稳定.以上实证分析表明ARIMAX-GARCH模型在股票预测中比两个单一模型更稳定，且效果更佳.

3 结语

股票作为金融市场最主要的金融产品，其价格能否被预测，以及用何种方法进行预测，一直以来都是金融领域研究的焦点问题.ARIMAX模型与GARCH模型是预测模型中的典型代表，两者在预测上均具有自己独特的优势.分析ARIMAX模型与GARCH模型的特性可知，两者具有极强的互补性，于是我们想到构造ARIMAX模型与GARCH模型的集成模型(ARIMAX-GARCH)来取长补短.在实证分析中，我们对10只股票收盘价在3个模型中预测效果的比较表明，ARIMAX-GARCH模型在股票预测中比两个单一模型更稳定，且效果更佳.

我们知道很多因素都会影响股票的收盘价，故输入变量序列中除交易量外还可以有很多其他变量，如何筛选变量，多变量间如何确定相互关系都有待于进一步研究.

[1]George EP Box,Gwilym M Jenkins.Time Series Analysis:Forecasting and Control[M].California:Holden-Day,1976.

[2]Robert F Engle,CWJ Granger.Co-Integration and Error Correction:Representation,Estimation and Testing[J].Econometrica,1987,55(2):251-276.

[3]Robert F Engle,Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation[J].Econometrica,1982,50(4):987-1007.

[4]Tim Bollerslev.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics，1986,31(3):307-327.

[5]唐齐鸣,陈健.中国股市的ARCH效应分析[J].世界经济,2001(3):29-36.

[6]高铁梅.计量经济分析方法与建模——Eviews应用及实例[M].北京:清华大学出版社,2006.

[7]熊志斌.基于ARIMAX与神经网络集成的GDP时间序列预测研究[J].数理统计与管理,2011,30(02):306-314.

Integrated Model ARIMAX GARCH and Its Applications in Stock Forecast

Shen Xiaoxin Zhao Yaling Zhu Haijiang

(Department of Statistics, Zhejiang Normal University, Jinhua, Zhejiang 321004)

Based on the analysis of the performance of multiple stationary time series of ARIMAX and GARCH models, this paper sets up a new model which integrates ARIMAX with GARCH. The new model has the advantage of regression in ARIMAX and the superiority of extracting volatility in GARCH. The result of empirical analysis about ten shares from five industries which are grabbed at random shows that the proposed model has better accuracy and stability in stock forecast than every single model.

time series; ARIMAX; GARCH; ARIMAX-GARCH; stock forecast

2014-08-22

沈小欣(1989-)，女，江苏泰州人.研究方向：数理统计.

F224.9；O213.9

A

1008-293X(2014)09-0060-04

(责任编辑邓颖)