凸函数导出指标

孙建新

(绍兴文理学院 数学系,浙江 绍兴312000)

凸函数导出指标

孙建新

(绍兴文理学院 数学系,浙江 绍兴312000)

讨论了凸函数导出指标的各种常见类型,考虑了它们与范数导出指标的关系,并通过实例对两者进行了比较.

凸函数;拉格朗日乘子法;信息熵;范数导出指标;凸函数导出指标

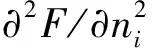
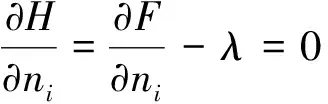
则该凸函数F(nj;pj,p,n)有资格作为离散资源公平分配的目标函数.由这样的目标函数所导出的指标,称之为凸函数导出指标,以便区别于在目标函数为范数(即广义的距离)的数学模型中的由范数导出的指标.

1 和函数导出的指标

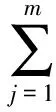
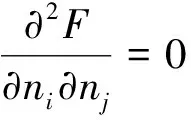
则x0为

根据基本初等函数的不同,常见的凸函数类指标可分为6种:

1.1凸函数F为pi/ni的加权幂函数之和

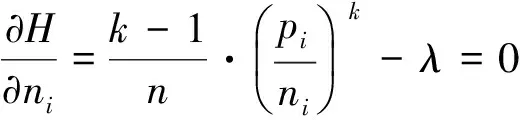
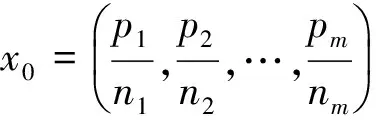
下面求凸函数F为pi/ni的加权幂时的比较指标.

不妨考虑j=1与j=2两个部门间的席位转让方案(其余部门不变)：

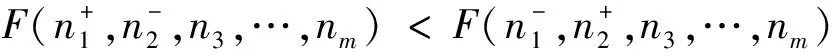
即

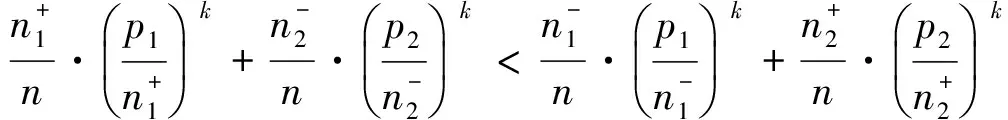
上式等价于

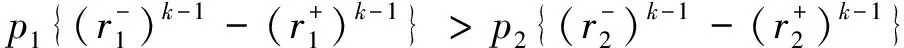
所以可取比较指标为

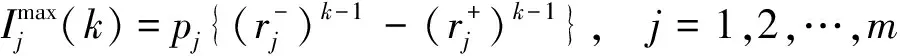
特别地，当k=2时，有

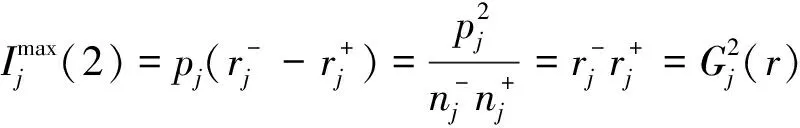
可见，指标Ijmax(2)与EP法的Huntington-Q值指标相当.

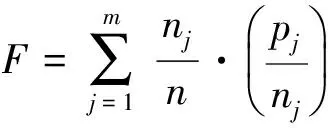
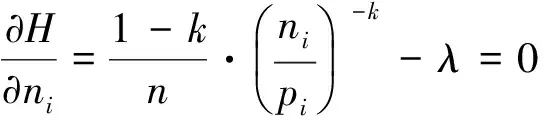
类似地，可取比较指标为

亦即

特别地，当k=-1时，有

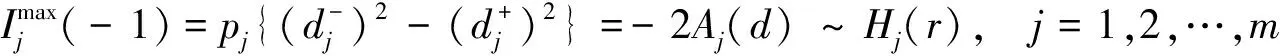
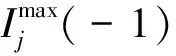
1.2凸函数F为pi/ni的加权对数函数之和

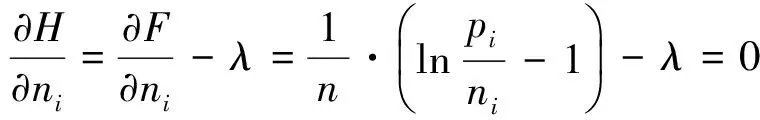
类似地，不妨考虑j=1与j=2两个部门间的席位转让方案(其余部门不变)：

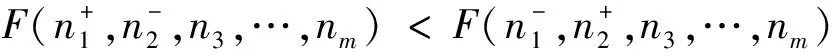
即

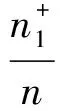
等价于

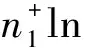
可得比较指标为

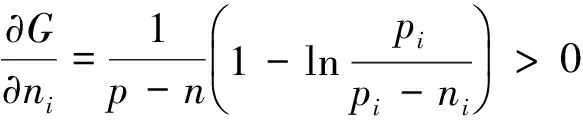
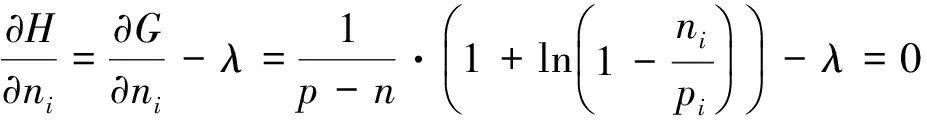
类似可得比较指标为

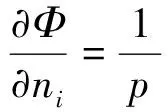
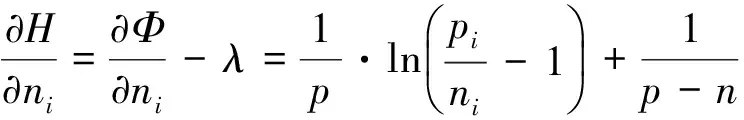
综合可得比较指标为

1.3凸函数F为pi/ni的加权指数函数之和

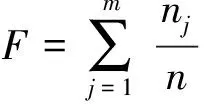
H=F+λ(n-∑nj),

则有

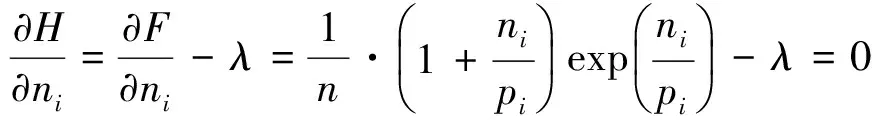
类似可得比较指标为

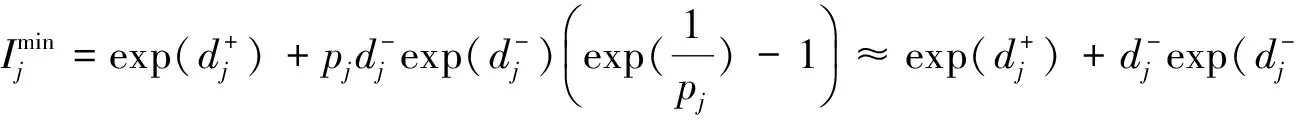
进一步的分析可知,当正数d≪0.1时，该指标与1+2Aj(d)很接近.于是该指标法与Webster方法的方案也很接近.

1.4凸函数F为pi/ni的加权正切函数之和

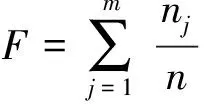
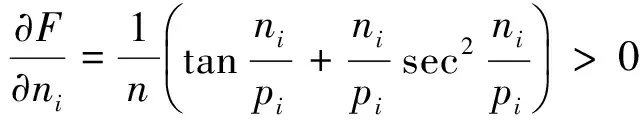
类似可得比较指标为

当正数d≪0.1时，该指标法与Webster方法也很接近.

1.5凸函数F为pi/ni的加权反正切函数之和

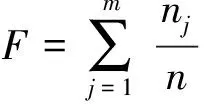
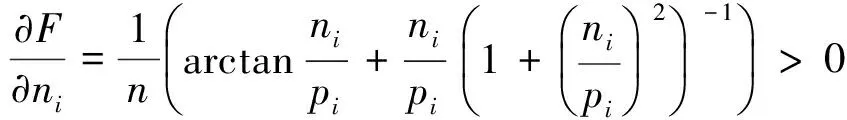
类似可得比较指标为

当正数d≪0.1时，该指标法与Webster方法也很接近.

2 乘积函数导出的指标

对凸函数F为pi/ni的幂指函数的乘积，设Ugt;0,则UV=exp(V·lnU),特别地:

(ⅰ)对于凸函数为

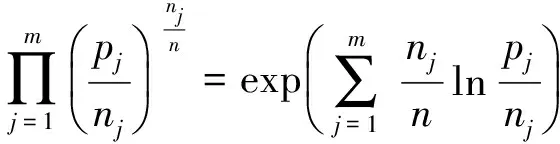
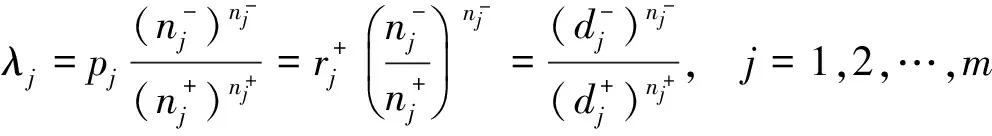
(ⅱ)对于凸函数为

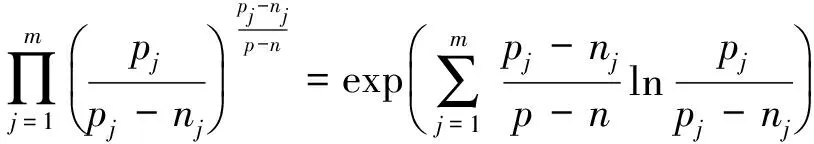
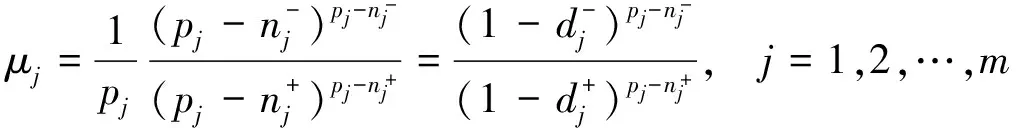
(ⅲ)对于凸函数为

3 离散分布函数导出的指标

3.1多项分布

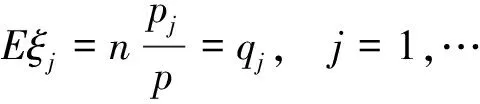
由极大似然原理，联合分布的概率达到最大的点就是(q1,q2,…,qm)，于是满足公平性条件.

下面求凸函数F为多项分布时的比较指标.

不妨考虑j=1与j=2两个部门间的席位转让方案(其余部门不变)：

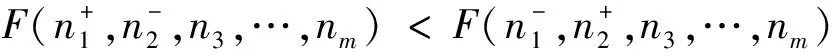
即

等价于

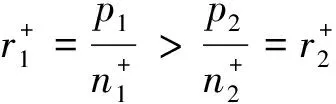
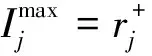
3.2多项超几何分布

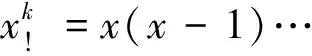
对于部门j来讲，就是二项超几何分布，即

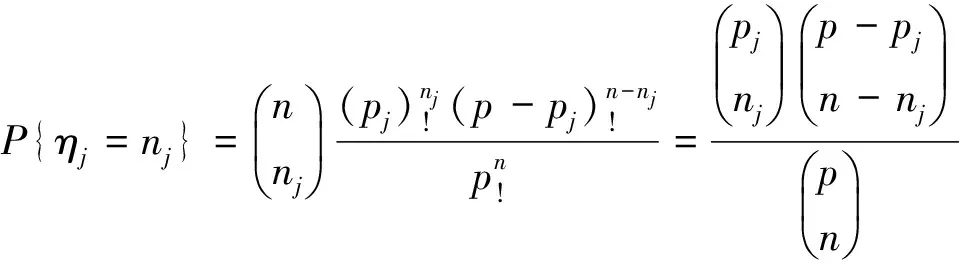
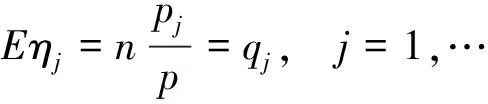
由极大似然原理，联合分布的概率达到最大的点就是(q1,q2,…,qm)，于是满足公平性条件.

下面求凸函数G为多项超几何分布时的比较指标.

不妨考虑j=1与j=2两个部门间的席位转让方案(其余部门不变)：

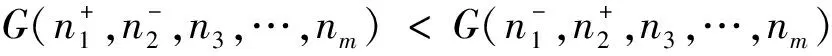
即

等价于

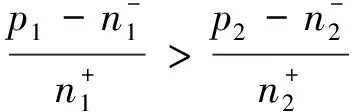
于是可得

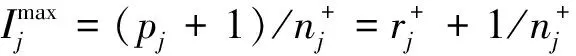
这表明由超几何分布导出的指标与多项分布导出的指标略有差异.

4 凸函数导出指标及其等价指标汇总

下面将凸函数导出的指标作一小结，结果见表1.

表1 凸函数类指标一览表

5 凸函数导出指标与范数导出指标的比较

例1 设m=3,n=10,p=100,p1=69,p2=16,p3=15.试使用指标λj，μj与νj求席位分配方案，并且与最大概率法、Jefferson方法和Webster方法的分配方案进行比较.

解已知m=3，n=10，p=100，p1=69，p2=16，p3=15.令

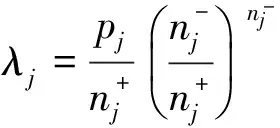
表2是6种不同方法指标及其所对应的分配方案的比较.由表2的计算结果可知，在某些情况下，信息熵法所得结果可能与Jefferson法相同，而与Webster法不同.由离散资源公平分配的理论[1-2]可知，当总席位不固定时,席位分配的最优方法是W法，即Webster法;总席位数固定时,最优方法为S法.所以，最大信息熵法[3]并非席位分配问题的最优方法，但是它应该是对称的服务指派问题的一种理想方法.

表2 6种方法的指标在实例中的分配方案比较

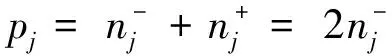
[1]孙建新.席位分配公理的相容性与完备性[J].数学的实践与认识，2011，41(4)：78-84.

[2]孙建新.On Fair Distribution of Discrete Resources[J].绍兴文理学院学报,2013，33(9)：8-22.

[3]高尚.席位分配的最大熵法[J].数学的实践与认识，1996，26(2)：73-75.

The Index Derived from Convex Function

Sun Jianxin

(Department of Mathematics, Shaoxing University, Shaoxing, Zhejiang 312000)

In this paper, the common types of index derived from various convex functions are discussed. The relationship between the index derived from norm and convex function are considered. Both of them are compared by example.

convex function; method of Lagrange multiplier; information entropy; index derived from norm; index derived from convex function

2014-07-08

孙建新(1946-)，男，浙江绍兴人，副教授.研究方向：离散数学与数学建模.

O224

A

1008-293X(2014)09-0001-07

(责任编辑邓颖)