静电悬浮加速度计反馈引起闭环点漂移机理及抑制方法
2014-10-24刘云峰董景新
刘 爽,刘云峰,董景新
(清华大学 精密仪器系 高精度导航技术教育部重点实验室,北京 100084)
静电悬浮加速度计反馈引起闭环点漂移机理及抑制方法
刘 爽,刘云峰,董景新
(清华大学 精密仪器系 高精度导航技术教育部重点实验室,北京 100084)
静电悬浮加速度计的检测质量闭环点位置偏离电极框中心时会造成系统非线性误差,调整检测电路输出电压可调整检测质量闭环点,而在调整过程中发现反馈电压变化会引起电容检测电路输出电压漂移,从而影响闭环点调节精度。为解决此问题,研究了闭环点位置与检测电路输出电压变化的关系,推导了检测电路传递函数,初步确定了反馈电压对检测电路输出电压影响的原因是隔直电容选取不恰当,通过实验对比了材料为C0G、Y5P、X7R及SL的多层陶瓷电容作为隔直电容时输出电压与反馈电压关系。实验结果表明:采用低温漂、耐高压和受频率影响小的C0G电容作为隔直电容能够消除反馈对检测电路引起的输出电压漂移,从而消除调节闭环点过程中闭环点位置的漂移,并且能提高检测电路稳定性。
非线性;闭环点漂移;C0G电容;静电悬浮加速度计

静电悬浮加速度计工作原理与 MEMS电容式静电加速度计工作原理类似,其闭环点位置对线性度具有重要影响[4],只有当检测质量闭环点位置位于电极框几何中心位置时,外界加速度才与反馈电压成线性。闭环点位置与检测电路输出电压的零偏及零偏波动有关。检测电路作用是将检测质量偏离中心位置时产生的差动电容转换成电压量,通常采用差动变压器式前端电路[5-6]。实际电路由于参数不对称,检测电路输出电压通常会存在一定的零偏值,使得检测质量闭环点位置偏离几何中心位置,从而造成系统非线性。因此需要调节检测质量闭环点,采用变预载闭环点调节方法可将闭环点调节到电极框中心[7-8]。变化的预载电压通过反馈通道经检测电路作用在表头。
在实验中发现,当直流高压作用在检测电路反馈端时,检测电路的开环输出电压会有几毫伏到十几毫伏漂移,相当于引起检测电路零偏的变化,因此在进行闭环点位置调节时,变化的预载电压(反馈电压)必会引起检测电路输出电压漂移,进而引起闭环点位置的漂移,带来闭环工作点调节误差。因此需要消除反馈电压对检测电路耦合作用。文献[9]分析了 LISA中惯性传感器前端电路反馈与检测交叉耦合原因是电路滤波电容选取不恰当,文献[10]报道了电容在高压、频率和温度下容值改变的实验现象。受其启发,我们设计检测电路也有可能是由于电容元件在高压作用下性质改变造成输出电压漂移。因此针对我们自行设计的检测电路,从理论上推导了反馈对检测电路输出耦合作用可能的原因,并通过实验进行验证,从而消除闭环点调节过程中闭环点漂移问题。
1 闭环工作原理及闭环点漂移来源
静电悬浮加速度计工作原理如图1所示:
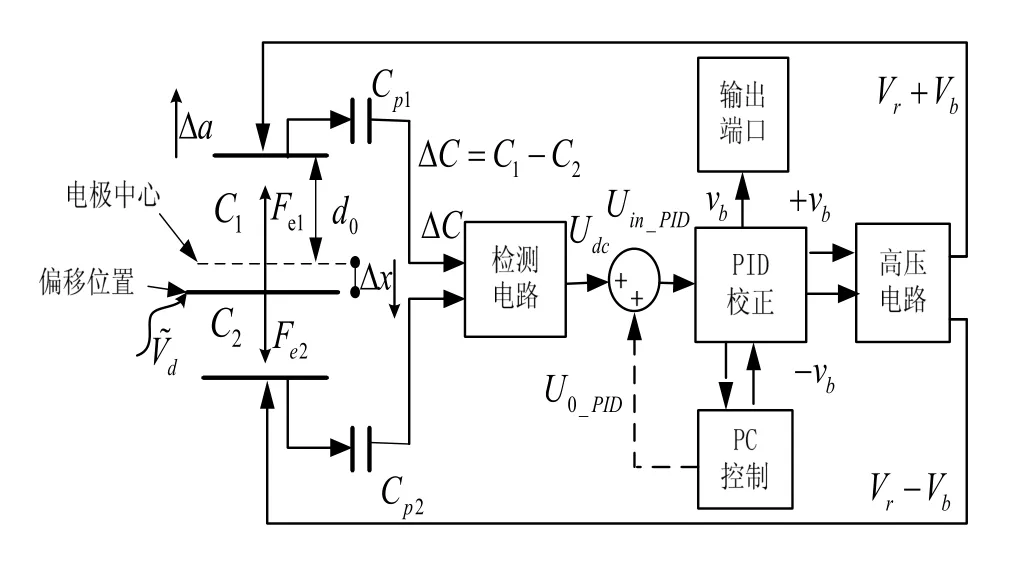
图1 静电悬浮加速度计工作原理图Fig.1 Schematic of electrostatically suspended accelerometer
检测电路输出端有如下电压关系:
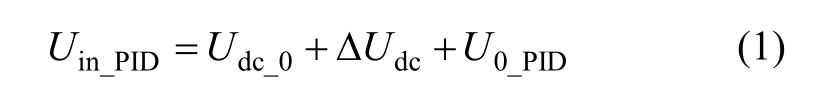
式中,Udc_0为检测电路零偏,ΔUdc为差动电容引起检测电路输出电压,二者构成检测电路输出电压 Udc;U0_PID为闭环校正电压;Uin_PID为PID输入电压。PID作用结果使得Uin_PID恒为零。
假设检测电路无零偏(Udc_0=0),检测质量闭环点位置位于电极框几何中心(Δx0=0),且未加校正电压(U0_PID=0)。当外界加速度引起质量块位置偏移Δx时,与上下电极板产生差动电容 ΔC,则经过检测电路转化成差动电压ΔUdc,经过PID控制电路和反馈高压电路在上下极板产生±Vb反馈电压。从而与预载电压Vr一起生成静电力Fe,拉动检测质量块回到初始位置,此时ΔC=0,因此ΔUdc=0。PID中积分器作用维持输出 Vb1产生静电力与外界力平衡。反馈电压与外界加速度呈线性关系。
若Udc_0≠0,PID控制作用仍然是使得Uin_PID=0,最终结果是产生反馈电压,生成静电力拉动检测质量块运动,使得质量块偏移中心位置位移为 Δx0,产生差动电容ΔC0,进而使得检测电路产生差动变化电压ΔUdc与Udc_0相抵消,以保证Uin_PID=0。显然此时质量块已经偏离几何中心位置,即产生闭环点位置偏移,造成系统非线性。
ΔUdc与Δx关系推导如下:
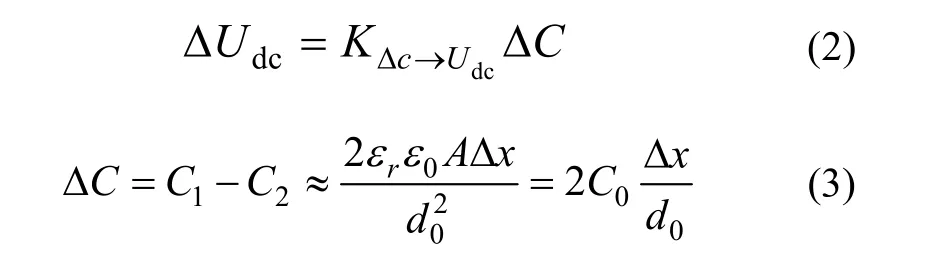
式中,KΔC→Udc为检测电路标度因数,C0为检测值质量位于几何中心;检测质量与单侧电极板形成电容值,即标称电容。联立式(2)(3),并且注意到ΔUdc+Udc_0=0,可得检测电路输出电压(零偏)与闭环点位置关系为:
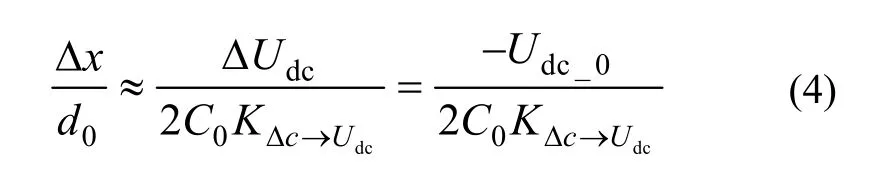
由于电路参数不对称,检测电路存在初始零偏,需要采用变预载闭环点调节方法对检测质量闭环点位置进行调节[7-8]。其基本原理如下:通过变化预载前后预载和反馈电压值,计算出闭环点偏移大小,从而计算出检测质量位于几何中心位置时的应有反馈电压值;调整U0_PID=0大小,便可调整检测质量在电极框中位置。检测质量位于不同位置时得到的反馈电压值不同,当实测的反馈电压值与计算出的反馈电压值相等时,检测质量便调整到几何中心位置。在调节闭环点时,发现变化的预载(反馈)电压引起检测电路开环输出电压漂移U′dc_0,进而引入额外的闭环点漂移 Δx′0,影响了闭环点调节精度。漂移大小可用式(4)计算。
在进行闭环点调节时,要求闭环点调节精度控制在 Δx/d0<10-4,代入表 1中数据,可得为满足上述要求时,X1、Y和Z2通道检测电路输出电压漂移应分别小于0.64 mV、0.96 mV和0.48 mV。而实验中发现检测电路开环时,反馈端接入直流高压时检测电路输出电压漂移达到几毫伏到十几毫伏漂移,因此严重影响了闭环点调节精度,需要解决反馈电压对检测电路输出电压的耦合作用。
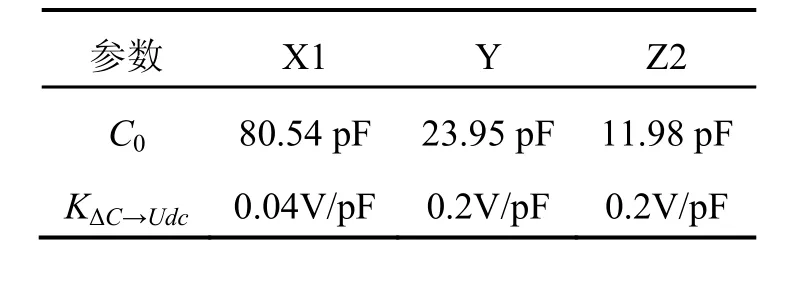
表1 X1、Y和Z2通道参数Tab.1 Parameters of X1, Y and Z2 channel
2 检测电路模型分析
为找到反馈对检测电路的耦合作用机理,需要从检测电路传递函数入手。静电悬浮加速度计检测电路原理图如图2所示,C1、C2为表头差动电容;表头置于真空腔内,表头电极和检测电路通过屏蔽线相连,Cs1、Cs2为屏蔽线对地寄生电容;反馈电压经电阻 Rb和滤波电容Cb分别加载到表头两端;Cp1、Cp2为高压隔直电容,防止反馈高压经过差动变压器并耦合到输出端,反馈电压最高可达1 kV,因此Cp1、Cp2采用耐高压多层陶瓷电容;L1、L2为差动变压器初级,L3为次级;Cg、Cf与运放一起构成电荷放大器,选频放大、乘法解调及低通滤波可等效为增益Kdc。
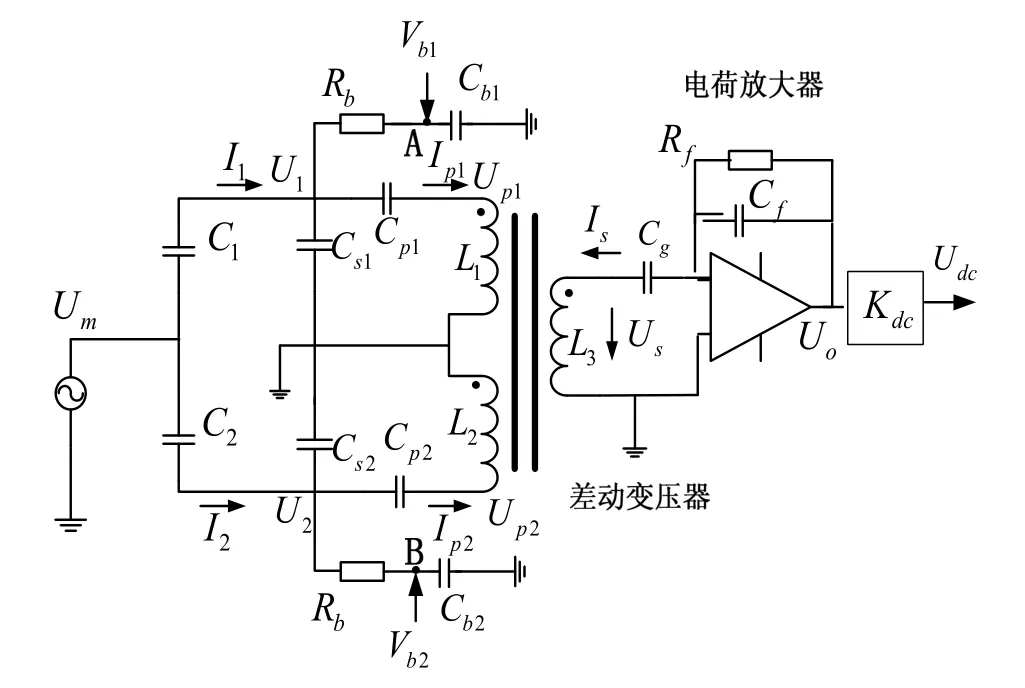
图2 电容检测电路原理图Fig.2 Schematic of the capacitive detector circuit
2.1 等效电压源分析
激励电压Um频率采用240 kHz,反馈电阻Rb(100 kΩ)的阻抗远大于Cp和Cs的交流阻抗。因此忽略反馈电阻对交流信号分流,仅考虑差动变压器和电荷放大器组成的交流电路模型。
由基尔霍夫电流、电压定律得:
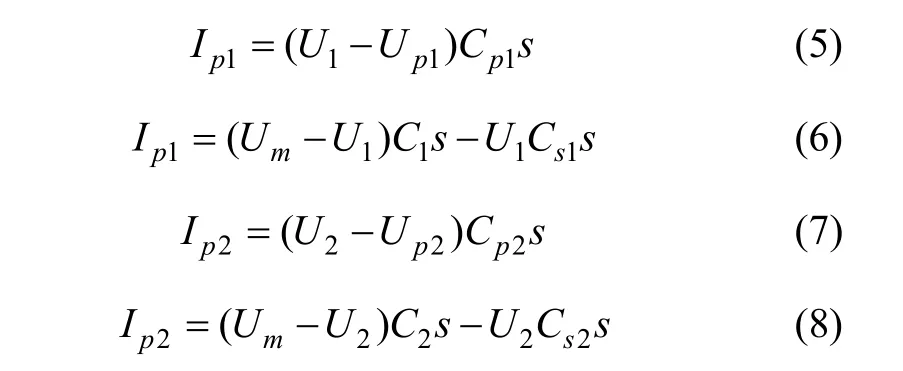
根据变压器耦合原理有:
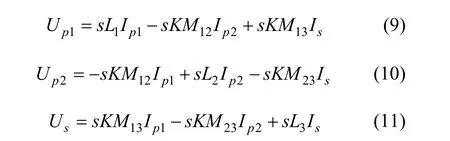
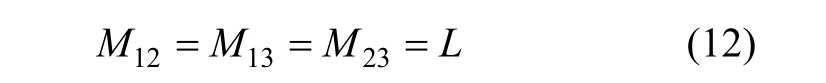
将式(9)~(12)联立,有:
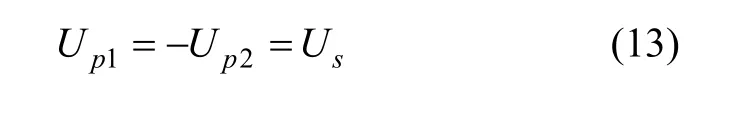
差动变压器可等效为一带内阻的电压源,等效电路如图3所示,UBR为差动变压器等效电压源,ZBR为等效阻抗。
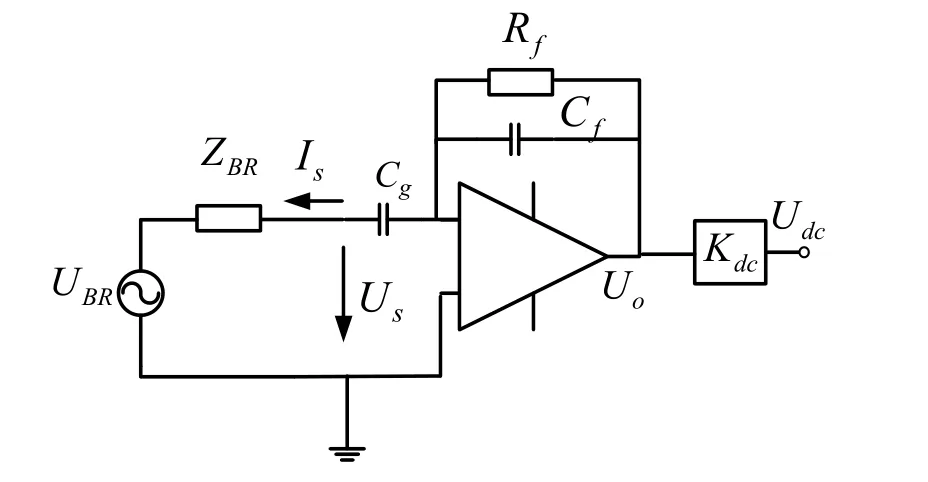
图3 等效检测电路Fig.3 The equivalent of detector circuit
为求等效电压源UBR大小,可将次级线圈开路,这时 UBR=Us,Is=0。联立式(5)~(8)、(11)~(13),并取Cs1=Cs2= Cs,Cp1=Cp2=Cp,ΔC=C1-C2得:
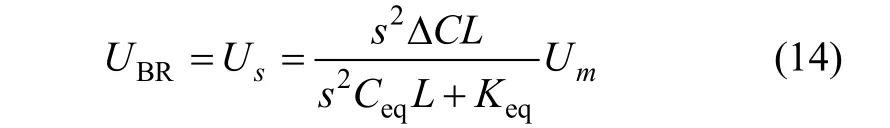
其中:
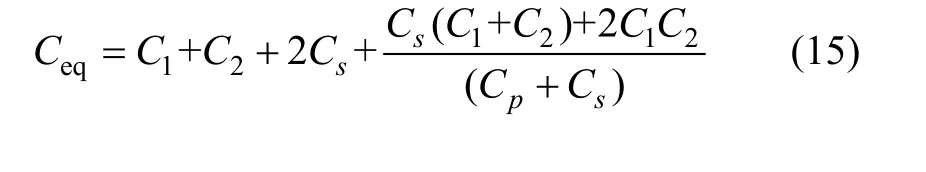
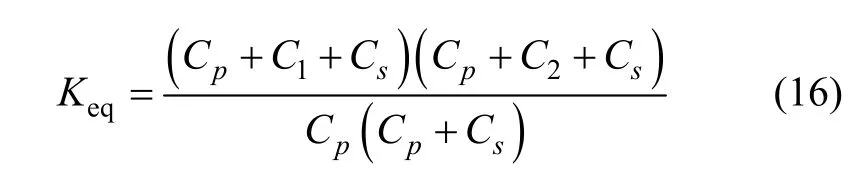
2.2 等效阻抗分析
如图3所示,当Us短路时,Us=0,此时可根据开路电压 UBR和短路电流 Is的比值计算变压器等效阻抗,如式(17)所示:
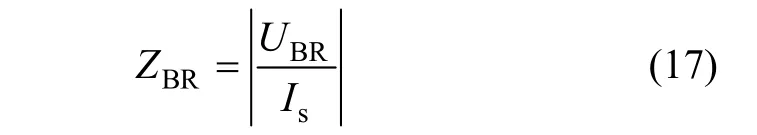
当 Us= 0时,由式(13)可知:
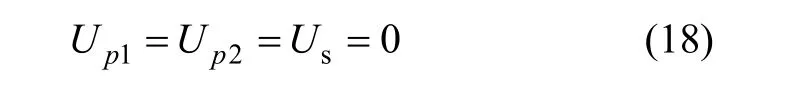
联立式(5)~(8)、式(11)和式(18)得:
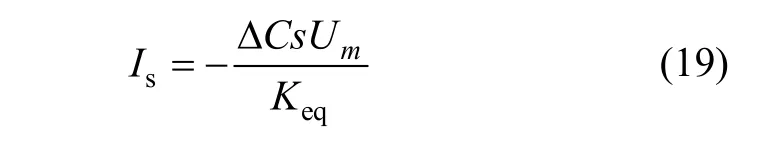
将式(14)和(19)代入(17)得:
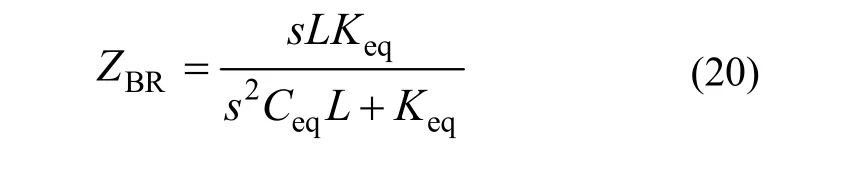
2.3 反馈对检测电路耦合影响机理分析
由图2可推导检测电路最终输出电压为:
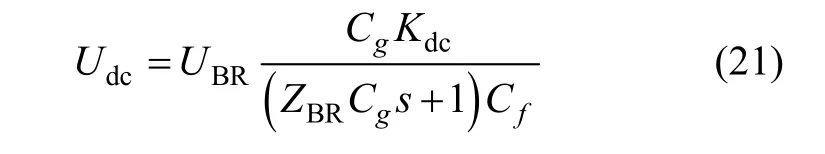
将式(14)(20)代入式(21),并令 s = jω得:
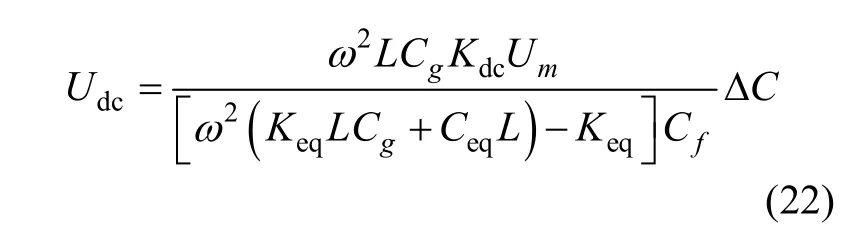
由Udc表达式可得如下结论:
● 在 Cs、Cp和 C0为定值时,Ceq、Keq为常数,其他参数也均为常数,此时检测电路输出电压 Udc只与差动电容ΔC有关,且为线性关系。
● 在共振频率 f0处,Udc达到最大值,共振频率表达式为:
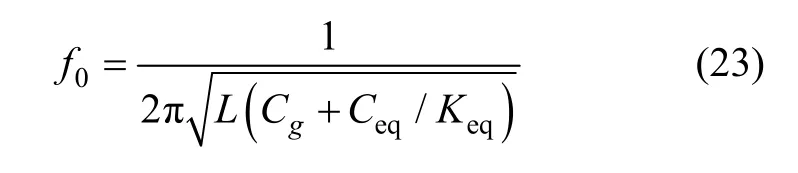
结合Ceq、Keq表达式可知:系统谐振频率由表头电容C1和C2、屏蔽线寄生电容Cs、隔直电容Cp、电荷放大器前端电容Cg、线圈电感L共同决定。任意一个变量改变均会引起系统谐振频率变化,进而引起检测电路传递函数和输出电压变化。
正常情况下,由于隔直高压电容Cp1、Cp2作用,反馈直流高压不会耦合到变压器次级,少量的交流反馈电压信号即使耦合到变压器次级,也会经过后续选频放大和乘法器解调和低通滤波大大衰减去除(乘法器解调频率240 kHz)。因此,实验中观察到反馈对检测电路耦合引起检测电路输出电压漂移原因最可能是反馈高压引起上述参数中某一参数改变,从而引起系统传递函数改变。
如图2所示,反馈高压作用在A、B两点,电感线圈和电荷放大器电容Cg依靠隔直电容Cp与高压隔离,因此可能改变参数的是反馈电压直接作用的C1、C2、Cs和Cp。而C1、C2为表头电容,Cs为屏蔽线对地分布电容,二者受高压影响可能性很小,最大可能就是隔直电容Cp受反馈高压作用电容值发生改变,从而影响 Udc。Cp采用的耐高压的多层陶瓷电容,材料为Y5P,文献[9-10]中报到过多层陶瓷电容在高压下介电常数改变的情况,因此对于我们设计的电路有可能是隔直电容 Cp受高压影响造成的检测电路输出电压漂移,需要通过实验进一步验证上述推论。
3 实验研究
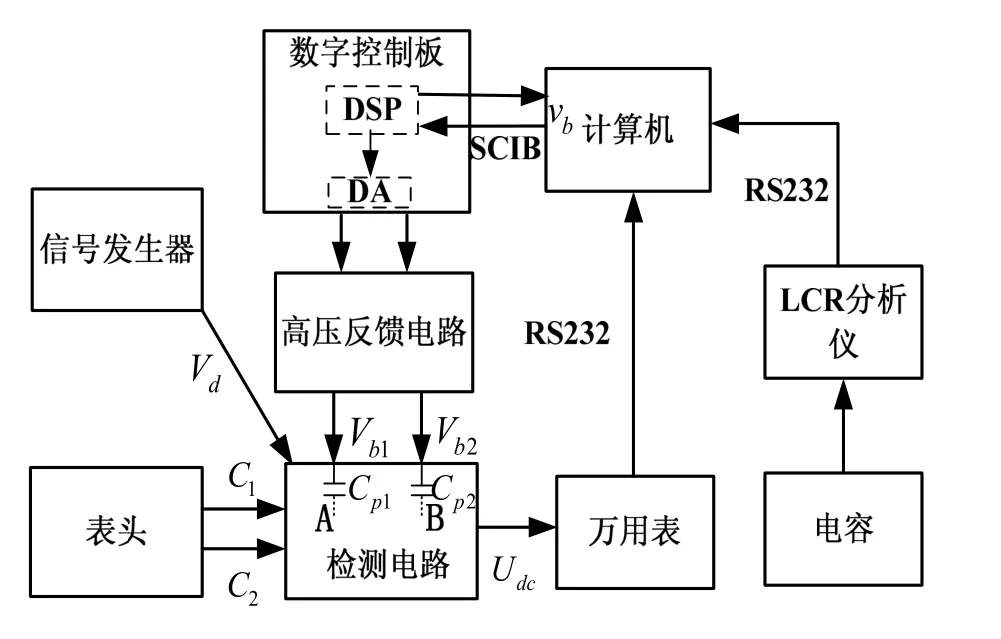
图4 实验装置框示意图Fig.4 Block diagram of experiment
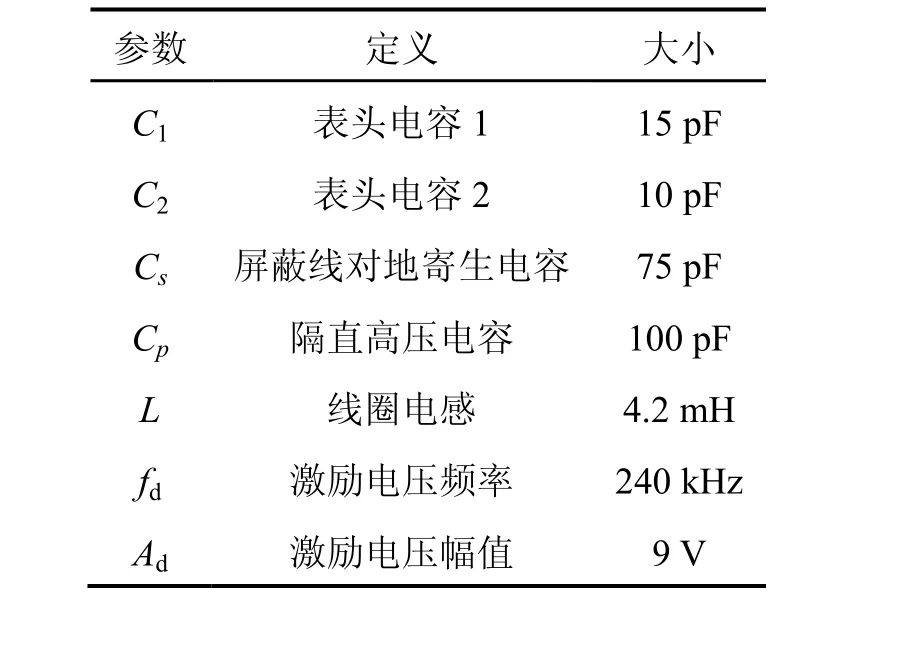
表2 实验中检测电路参数Tab.2 Parameters of detector electronics circuit
采用不同Cp电容做对比实验。实验装置示意图如图4所示,电路参数如表2所示,采用标称电容同为100 pF的不同材料的多层陶瓷电容(见表3)替换Cp1和Cp2。之前电路的Cp采用的是Y5P(Y5P2)电容,发现具有耦合现象。C0G电容被证实具有低温漂、耐高压等特点,容值几乎不随外界影响而发生改变[9-10],可作对比试验。所采用电容均为耐高压电容。
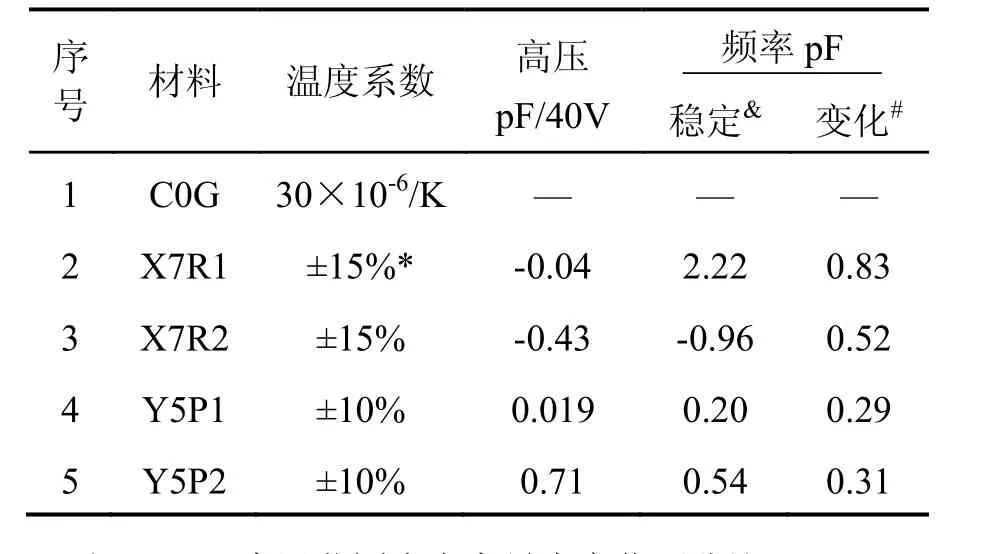
表3 不同型号电容参数Tab.3 Parameters of different capacitors
Cp1和Cp2采用Y5P(Y5P2)或C0G电容在高压下实验结果如图5所示。可见当大小为40 V的反馈电压单独作用在Cp1或Cp2时,均会使得检测电路输出电压Udc发生跳变,幅度最大变化20 mV左右,且改变趋势相反,与反馈电压正负极性无关,且 Udc跳变量随着时间衰减;当反馈电压同时作用在Cp1和Cp2时,对检测电路产生的影响可以抵消一部分,但由于电容差异不能完全抵消,Udc仍然存在5 mV左右的跳变。上述现象说明了反馈电压对检测电路耦合作用引起检测电路输出电压漂移,从而影响系统闭环点位置。
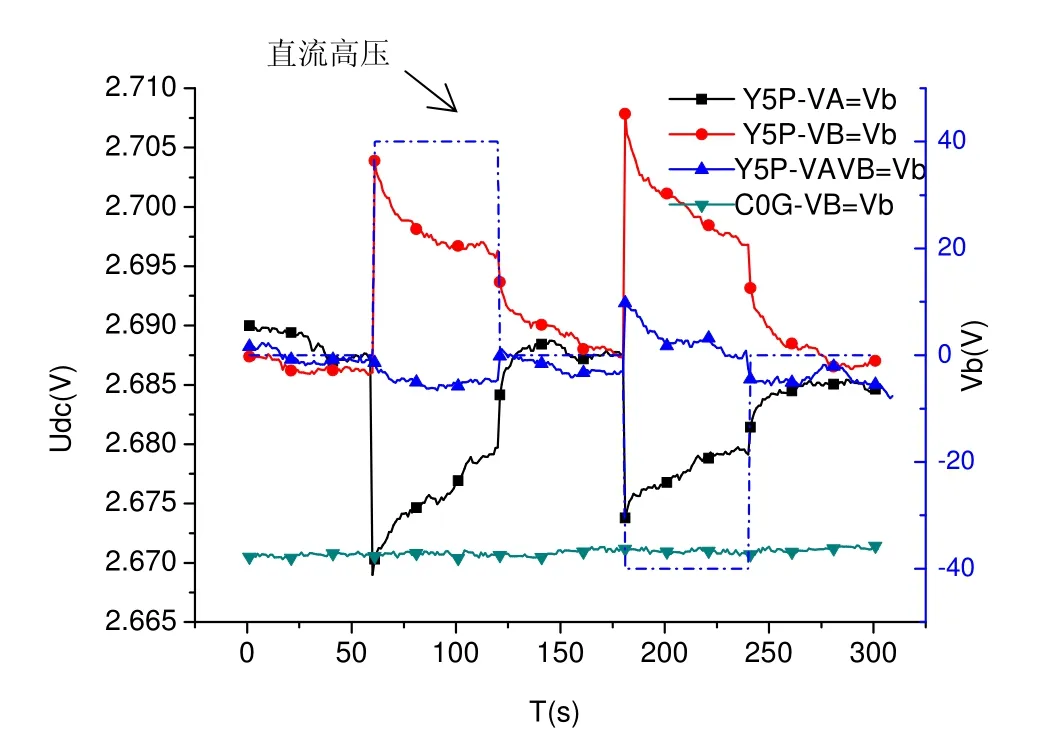
图5 采用Y5P或C0G电容时Udc与Vb关系Fig.5 The Udc for Y5P or C0G under Vb
当Cp1和Cp2采用C0G电容时,Udc没有明显变化。
以上实验结果证实了反馈对检测电路耦合作用是由于Cp在高压作用下容值改变造成的,与之前理论分析相符。采用C0G电容时,在进行变预载闭环点调节时,不会引起闭环点位置漂移,解决了变预载过程中闭环点漂移问题。
图6所示Cp2采用不同容值C0G,得到Udc与Cp2线性关系,可见当 Cp2增加时,检测电路输出电压增加,因此可以根据检测电路输出电压变化,判断 Cp2电容增大或减小,通过线性拟合得到ΔCp2与ΔUdc的比例系数KC-U=0.03869 V/pF,进而可求出Cp2在反馈高压作用下改变量。
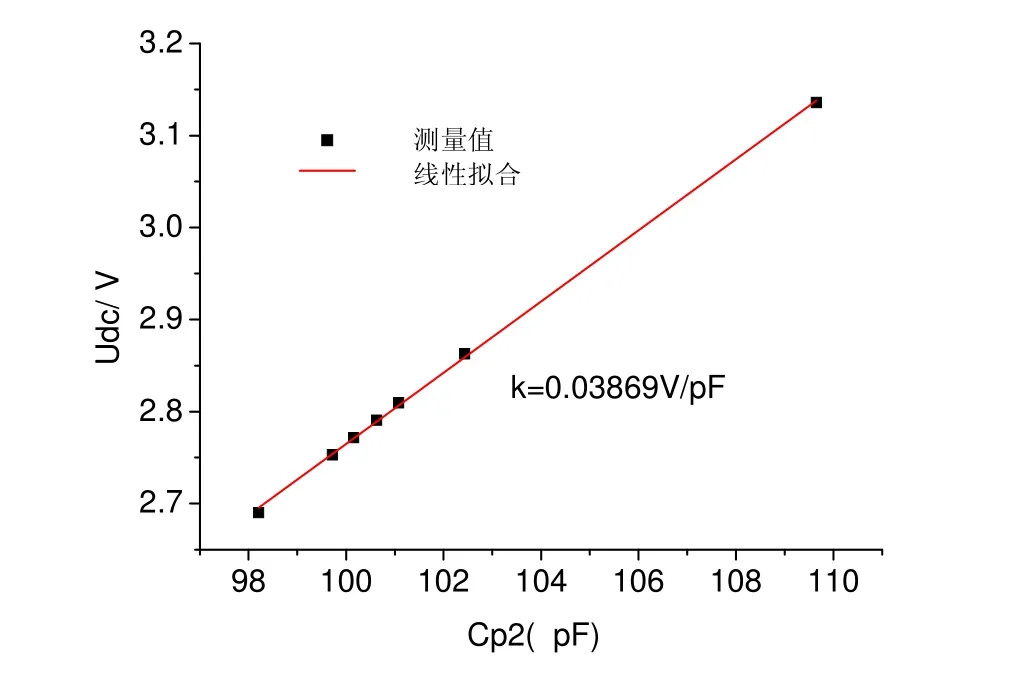
图6 Udc与Cp2关系Fig.6 The relationship between Udc and Cp2
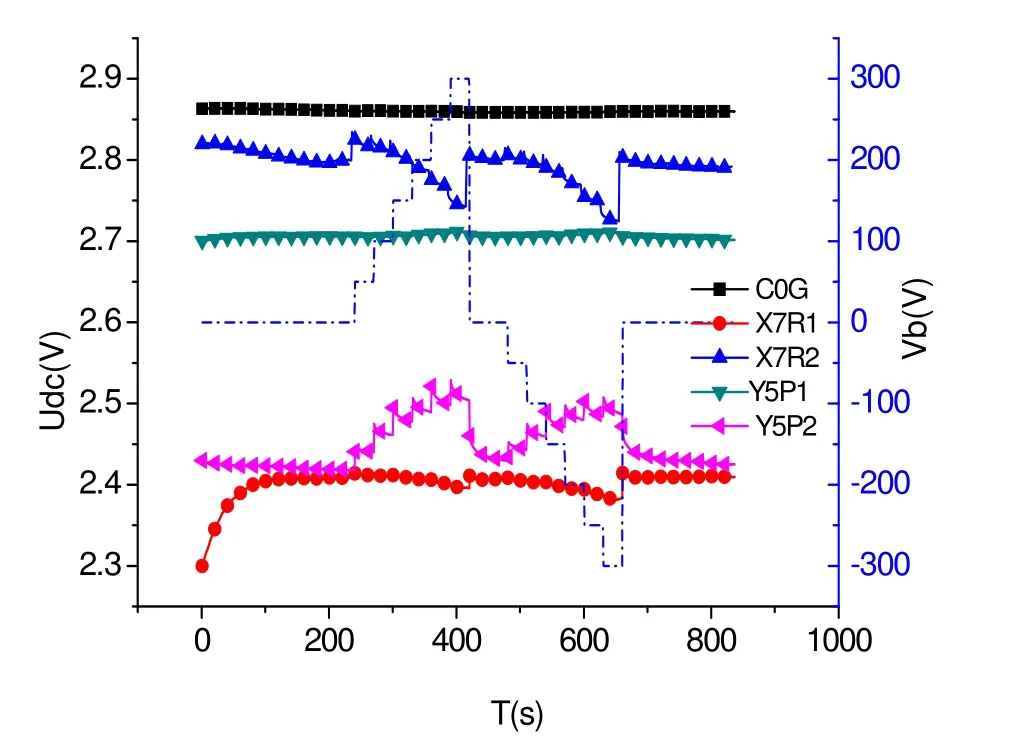
图7 不同电容在不同电压下Udc值Fig.7 The Udc under different Vb with different Cp
Cp1采用C0G电容,Cp2采用不同材料电容,得到不同Vb作用下Udc结果如图7所示。可见电压在0~300 V范围变化时,C0G电容大小几乎不变;其他几种电容均受高压影响,且影响大小不一致,且 Udc并不为常数,而是随时间衰减,说明上述电容值受高压影响存在非线性关系。根据KC-U和ΔUdc可以求出每40 V高压作用下电容改变量大小,结果如表3所示。
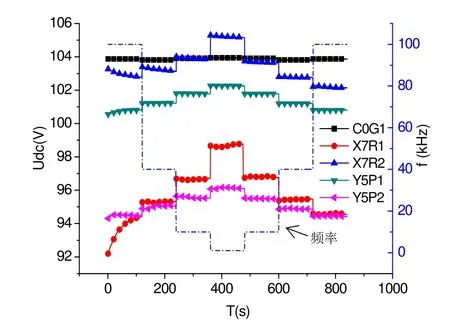
图8 不同频率下电容值Fig.8 Capacitances under different frequencies
由图7和表3中电容受高压影响实验结果可知,同种材料的多层陶瓷电容由于厂家不同,受高压改变量也不一致。
为研究电容与频率关系,利用LCR分析仪在幅值1 V、不同频率下测量电容随频率变化关系,实验结果如图8。由图8可见,除C0G外,其他几种电容均随频率变化。图5和图7曲线开始阶段的漂移也是由于电容刚接入电路时受频率影响容值改变而造成检测电路输出电压漂移,因此频率变化也会引起电容容值变化,从而对检测电路输出产生影响,引起闭环点位置漂移。电容受频率影响具体数值见表3。
此外多层陶瓷电容还受温度影响,从而引起检测电路输出电压漂移,温度影响情况同样汇总于表3[10]。
本文开始提到,在进行静电悬浮加速度计闭环点调节时,闭环点调节精度在10-4量级,X1、Y和Z2通道电路输出电压漂移应分别小于0.64 mV、0.96 mV和0.48 mV,再根据KC-U可得Cp变化应分别小于0.017 pF、0.025 pF和0.012 pF。
因此综合考虑高压、温度和频率的影响,上述电容中只有C0G电容满足要求。因此将Cp电容材料由原来的Y5P替换为C0G解决了变预载过程中闭环点位置漂移问题,有助于实现闭环点精确调节,此外还能够提高检测电路稳定性,降低噪声。
4 结 论
本文通过理论和实验研究确定了反馈电压造成检测电路输出电压漂移的原因是检测电路隔直电容选取不恰当。采用C0G电容替代原有Y5P电容,消除了反馈电路对检测电路间耦合作用,从而解决了变预载闭环点调节过程中闭环点位置漂移的问题。同种材料、不同厂家的多层陶瓷电容受高压、频率和温度影响不一致,C0G电容受上述因素影响最小,因此选用此电容有助于提高检测电路整体性能。
(
):
[1] Danzmann K. LISA—an ESA cornerstone mission for the detection and observation of gravitational waves[J]. Advances in Space Research, 2003, 32(7): 1233-1242.
[2] Hudson D, Chhun R, Touboul P. Development of a differential accelerometer to test the equivalence principle in the microscope mission[J]. Acta Astronautica, 2005, 57(2): 341-347.
[3] Touboul P, Foulon B, Christophe B, et al. CHAMP, GRACE, GOCE instruments and beyond[J]. Geodesy for Planet Earth, 2012, 136: 215-221.
[4] Wan Caixin, Dong Jingxin, Liu Yunfeng, et al. Nonlinearity of a closed-loop microaccelerometer[C]//2007 IEEE International Conference on Control Applications. Singapore, 2007: 1260-1265.
[5] Josselin V, Touboul P, Kielbasa R. Capacitive detection scheme for space accelerometers applications[J]. Sensors and Actuators A: Physical, 1999, 78(2): 92-98.
[6] Bai Yanzheng, Zhou Zebing, Tu Haibo, et al. Capacitive position measurement for high-precision space inertial sensor[J]. Frontiers of Physics in China, 2009, 4(2): 205-208.
[7] Fan Da, Liu Yunfeng, Han Fengtian, et al. Identification and adjustment of the position and attitude for the electrostatic accelerometer's proof mass[J]. Sensors and Actuators A: Physical, 2012, 187: 190-193.
[8] 范达. 星载静电悬浮加速度计的设计与地面实验研究[D]. 北京:清华大学,2013.
FAN Da. Design and ground experimental study of a spaceborne electrostatic levitated accelerometer[D]. Beijing: Tsinghua University, 2013.
[9] Gan L, Mance D, Zweifel P. Actuation to sensing crosstalk investigation in the inertial sensor front-end electronics of the laser interferometer space antenna pathfinder satellite[J]. Sensors and Actuators A: Physical, 2011, 167(2): 574-580.
[10] Prymak J, Randall M, Blais P, et al. Why that 47 μF capacitor drops to 37 μF, 30 μF, or lower[C]//Proc. of the CARTS USA Conference. March 2008.
Mechanism and suppression method for feedback-caused close-loop position fluctuation of electrostatically suspended accelerometer
LIU Shuang, LIU Yun-feng, DONG Jing-xin
(Key Laboratory for High-precision Navigation Technology of Ministry of Education, Department of Precision Instrument, Tsinghua University, Beijing 100084, China)
The nonlinearity of electrostatically suspended accelerometer (ESA) is related to the closed-loop position of proof mass (Pm), which can be adjusted by changing the output of detection circuit (Udc). It is found that Udccan be changed by feedback voltage (Vb) during the adjustment, thus causing the fluctuation of Pm. In order to solve this problem, the relationship between Pmand Udcis studied, and the transform function of detection circuit is deduced. The contrast test is carried out with C0G, Y5P, X7R and SL capacitances under different Vband frequencies. Theoretical and experimental results show that the reason for the fluctuation of Udccaused by Vbis the variation of the isolation capacitance caused by Vb. Using the C0G capacitance, which is immune to temperature and high voltage and frequency, not only could overcome the fluctuation of Pmduring adjustment, but also improve the stability of the detector circuit.
nonlinearity; closed-loop position fluctuation; C0G capacitance; electrostatically suspended accelerometer
1005-6734(2014)05-0682-06
10.13695/j.cnki.12-1222/o3.2014.05.024
U666.1
A
2014-06-06;
2014-09-19
清华大学自主科研计划(20091081243)
刘爽(1985—),男,博士研究生,从事微重力关键技术研究。E-mail:s-liu08@mails.tsinghua.edu.cn
联 系 人:董景新(1948—),男,教授,博士生导师。E-mail:dongjx@mail.tsinghua.edu.cn
